1 度分佈

網路的度分佈\(p(k)\)表示了一個隨機選擇的節點擁有度\(k\)的概率。我們設度為\(k\)的節點數目\(N_k = \sharp\text{ nodes with degree } k\)，除以節點數量\(N\)則可得到歸一化後的概率質量分佈：

\[P(k)=N_k / N(k\in \mathbb{N}) \]

我們有：\(\sum_{k \in \mathbb{\mathbb{N}}} P(k)=1\)。
對於下面這個網路：

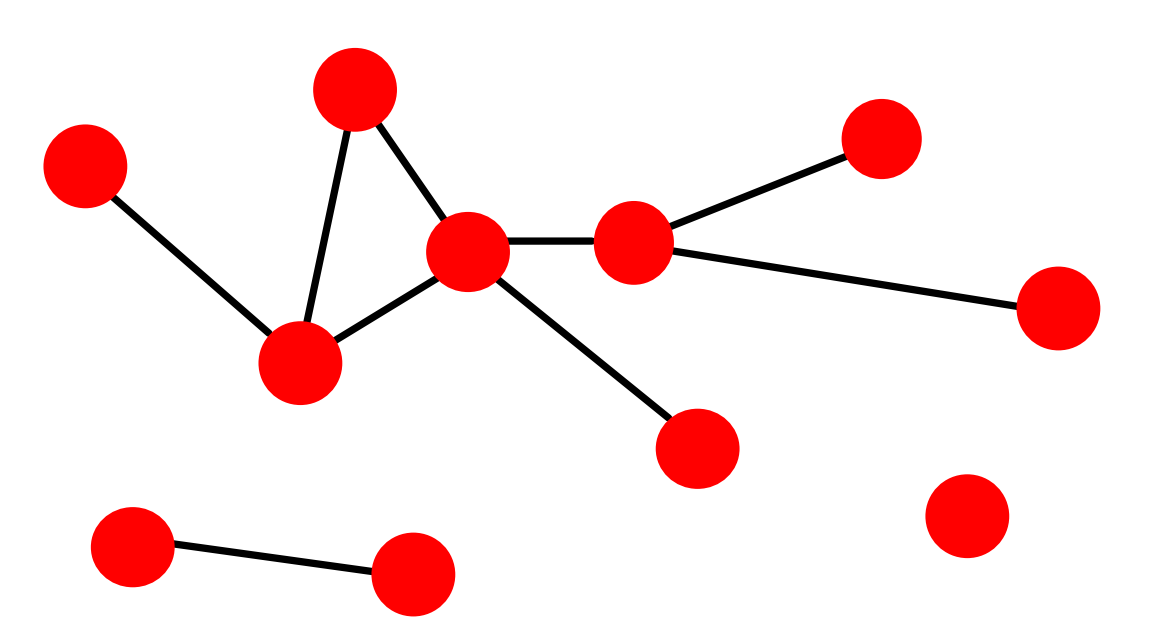
其歸一化後的度分佈直方圖可表示如下：

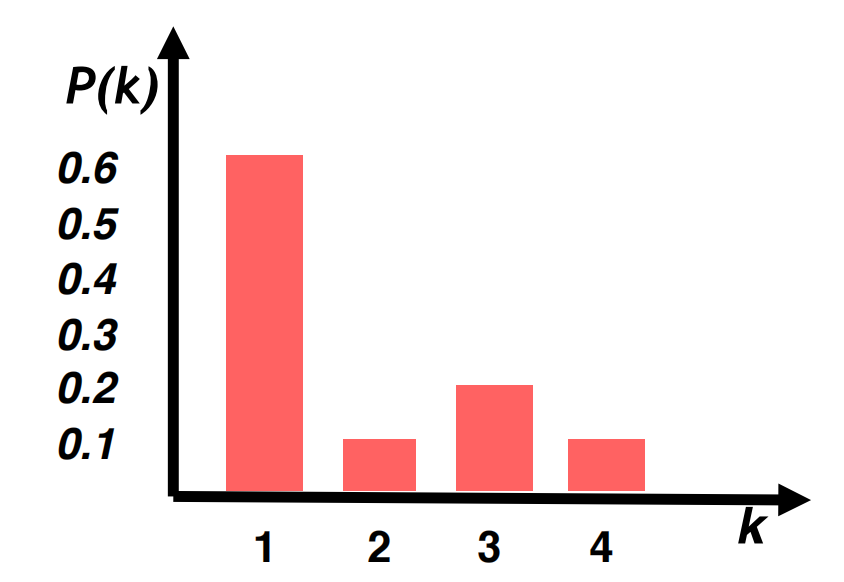
2 路徑

2.1 圖的路徑

圖的路徑(path)指一個節點序列，使得序列中的每個節點都連結到序列中的下一個節點(注意：這裡的術語不同教材不一樣，有的教材把這裡的路徑定義為漫遊(walk)，而將術語「路徑」保留給簡單路徑)。路徑可以用以下方式進行表示：

\[P_n=\left\{i_0, i_1, i_2, \ldots, i_n\right\} \quad P_n=\left\{\left(i_0, i_1\right),\left(i_1, i_2\right),\left(i_2, i_3\right), \ldots,\left(i_{n-1}, i_n\right)\right\} \]

一個路徑可以通過經過同一條邊多次而和它自身相交。如下面這個圖中更多路徑ABDCDEG就和自身相交。

注意，在有向圖中路徑只能沿著邊的方向。

2.2 路徑的條數

路徑的條數定義為節點\(u\)和\(v\)之間的路徑數量。我們發現鄰接矩陣的冪和路徑的條數之間有著關係。

長度 \(h=1\)(這裡的h可理解為跳數hops)的路徑計數矩陣: 只需要考察\(u\)和\(v\)之間是否存在長度為\(1\)的連結，即
\[H_{uv}^{(1)} = A_{uv} \]
長度 \(h=2\)的路徑計數矩陣：需要考察\(u\)和\(v\)之間是否存在長度為\(2\)的路徑，即對滿足\(A_{u k}A_{k v}=1\)的\(k\)進行計數。
\[H_{u v}^{(2)}=\sum_{k=1}^N A_{u k} A_{k v}=\left[A^2\right]_{u v} \]
長度 \(h\)的路徑計數矩陣：需要考察\(u\)和\(v\)之間是否存在長度為\(h\)的路徑，即對滿足\(A_{u k_1} A_{k_1 k_2} \ldots . A_{k_{h-1} v}=1\)的所有\(\langle k_1,k_2,\cdots, k_{h-1}\rangle\)序列進行計數。
\[H_{u v}^{(h)}=\left[A^h\right]_{u v} \]

上述結論對有向圖和無向圖都成立。上述定理解釋瞭如果\(u\)和\(v\)之間存在最短路徑，那麼它的長度就是使\(A^k_{uv}\)非零的最小的\(k\)。
進一步推論可知，在一個\(n\)個節點的圖中找到所有最短路徑的一個簡單方法是一個接一個地對圖的鄰接矩陣\(A\)做連續的冪計算，知道第\(n-1\)次，觀察使得每一個元素首次變為正值的冪計算。這個思想在Folyd-Warshall最短路徑演演算法中有著重要應用應用。

2.3 距離

圖中兩個節點之間的距離(distance)定義為兩個點最短路徑中的邊數（如果兩個點沒有連通，距離通常定義為無窮大）。
如對下面這個圖我們有\(B\)、\(D\)之間的距離\(H_{B,D}=2\)，\(A\)、\(X\)之間的距離\(h_{A, X}=\infty\)。

注意，在有向圖中距離必須沿著邊的方向。這導致有向圖中的距離不具有對稱性。比如下面這個圖中我們就有\(h_{A, C} \neq h_{C, A}\)。

我們定義兩兩節點之間距離的最大值為圖的直徑（diameter）。

2.4 平均路徑長度

無向連通圖（連通分量）或有向強連通圖（強連通分量）的平均路徑長度（average path length）定義為：

\[\bar{h}=\frac{1}{2 E_{\max }} \sum_{i, j \neq i} h_{i j} \]

這裡\(h_{ij}\)是節點\(i\)到\(j\)的距離。\(E_{max}=\frac{n(n-1)}{2}\)，這裡\(2E_{max}\)中的係數\(2\)可要可不要，不同教材定義方法不一樣。
在計算平均路徑長度時，我們通常只計算連通節點之間的距離（也即忽略長度為「無窮」的路徑）

2.5 尋找最短路徑

對於無權圖，我們可以由寬度優先搜尋(BFS)搜尋圖的最短路徑。

從節點\(u\)開始，將其標註為\(h_u(u)=0\)，並將其加入佇列。
當佇列不為空時：
- 將隊首元素\(v\)移出佇列，將其未標註的鄰居加入佇列並標註為\(h_u(w) = h_u(v) + 1\)。
- 迴圈往復。

對於帶權圖，我們當然就得尋求Dijkstra、Bellman-Ford等演演算法啦,此處不再贅述.

3 聚類係數

節點\(i\)的聚類係數(clustering coefficient)可以直觀地理解為節點\(i\)的鄰居有多大比例是互相連線的。設節點\(i\)的度為\(k_i\)，則其聚類係數\(C_i\)定義為

\[C_i=\frac{2 e_i}{k_i\left(k_i-1\right)} \]

這裡\(e_i\)為節點\(i\)鄰居之間的邊數，我們有\(C_i\in[0, 1]\)。下面展示了聚類係數的一些範例：
遷移學習和多工學習之間的區別

圖的平均聚類係數（average clustering coefficient）定義為：

\[C=\frac{1}{N} \sum_i^N C_i \]

4 真實世界網路的屬性

接下來我們來看一MSN收發資訊網路(有向)的範例。

該網路中245 million使用者註冊，180 million使用者參與了聊天，擁有超過30 billion個回話。超過 255 billion條互動資訊。
連通性

度分佈
遷移學習和多工學習之間的區別

其度分佈高度傾斜，平均度為\(14.4\)。

log-log度分佈

聚類係數

這裡為了方便出圖，我們定義橫座標為度\(k\)，對應的縱座標\(C_k\)為度為\(k\)的節點的聚類係數\(C_i\)的平均值，即\(C_k=\frac{1}{N_k} \sum_{i: k_i=k} C_i\)。

整個網路的平均聚類係數為\(0.11\)。

距離分佈

其中平均路徑長度為\(6.6\)，\(90\%\)的節點可以在\(8\)跳之內到達。

參考

[1] http://web.stanford.edu/class/cs224w/
[2] Easley D, Kleinberg J. Networks, crowds, and markets: Reasoning about a highly connected world[M]. Cambridge university press, 2010.
[3] Barabási A L. Network science[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2013, 371(1987): 20120375.
[4] 《圖論概念梳理》

圖資料探勘（二）：網路的常見度量屬性