好多同學跑來問，用spss的時候使用多重插補的資料集，怎麼選怎麼用？是不是簡單的選一個做分析？今天寫寫這個問題。

什麼時候用多重插補

首先回顧下三種缺失機制或者叫缺失型別：

上面的內容之前寫過，這兒就不給大家翻譯了，完全隨機缺失，缺失量較小的情況下你直接扔掉或者任你怎麼插補都可以，影響不大的。隨機缺失可以用多重插補很好地處理；非隨機缺失，任何方法都沒得救的，主分析做完之後自覺做敏感性分析才是正道；這個我好像在之前的文章中給大家解釋過原因。

When it is plausible that data are missing at random, but not completely at random, analyses based on complete cases may be biased. Such biases can be overcome using methods such as multiple imputation that allow individuals with incomplete data to be included in analysesly, it is not possible to distinguish between missing at random and missing not at random using observed data. Therefore, biases caused by data that are missing not at random can be addressed only by sensitivity analyses examining the effect of different assumptions about the missing data mechanism

多重插補的思想

寫多重插補之前我們先回憶簡單插補，叫做single imputation，就是缺失值只插一個，無論是用均值，用中位數，用眾數等等，反正只挑一個，只形成一個完整資料集，叫做簡單插補。

這裡面就有一個問題：就插了一個值，你怎麼就敢說這個值對？是不是偏倚的可能性其實挺高的？

多重插補就不一樣了，進行多重插補的時候我會對一個缺失值會插補很多個可能的值，我們會得到很多個完整的資料集（mutliple），比如每個缺失的地方我們插補5個值，就會得到5個資料集。這5個資料集的原來的缺失的資料都被演演算法插補好了，但是插補的值不盡相同，多重插補的思想精髓在於：對這插補出來的每一個資料集都做一遍我們的目標分析，然後將效應彙總從而得到誤差最小的合併效應。

現在給出多重插補的定義（來自BMJ）：

Multiple imputation is a general approach to the problem of missing data that is available in several commonly used statistical packages. It aims to allow for the uncertainty about the missing data by creating several different plausible imputed data sets and appropriately combining results obtained from each of them.

具體的思路就是，首先插補多個資料集，就是每個缺失的地方會插補多次，每一次插補的值都是基於現有資料分佈的缺失值的預測值；第一步做完之後我們不是有很多個完整資料集了嘛，然後我們將我們感興趣的分析在每一個資料集中都做一次，得到多個結果；第三步就是將這些結果彙總。

以上就是思路流程。

In the first step, the dataset with missing values (i.e. the incomplete dataset) is copied several times. Then in the next step, the missing values are replaced with imputed values in each copy of the dataset. In each copy, slightly different values are imputed due to random variation. This results in mulitple imputed datasets. In the third step, the imputed datasets are each analyzed and the study results are then pooled into the final study result.

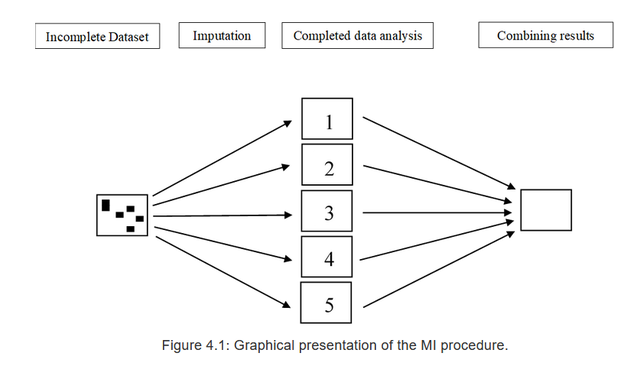
所以說如果你用多重插補處理缺失資料，分析的時候卻只用某一個資料集來做分析肯定都是不正確的，所以以後千萬別問，到底選哪個這樣的問題了，選哪個都不對。

介紹完思想我們再看實操。

範例操練

在spss中的多重插補實操，大家請閱讀下面的連結，寫的很細哈：

https://bookdown.org/mwheymans/bookmi/multiple-imputation.html#:~:text=After%20multiple%20imputation%2C%20the%20multiple%20imputed%20datasets%20are,that%20separates%20the%20original%20from%20the%20imputed%20datasets.

今天我們寫如何在R中進行多重插補

我現在有資料如下：

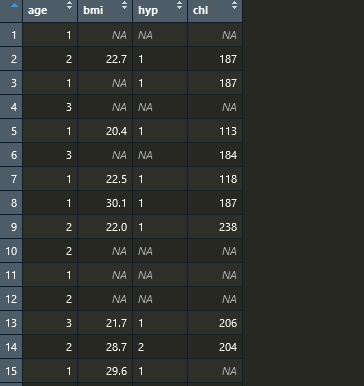
很簡單的資料，可以看到資料中有很多缺失值的，我想要做的目標分析是一個以hyp為因變數的邏輯迴歸，如果我不插補資料直接做，可以寫出如下程式碼：

model <- glm(hyp ~ bmi, family = binomial(link = 'logit'), data)
model_or <- exp(cbind(OR = coef(model), confint(model)))

執行後得到想要的OR和置信區間如下：

跑出來結果了，但是你要明白這個時候模型是預設將有缺失值的觀測刪掉的。結果不一定對。

現在我們對剛剛的資料集進行一個多重插補，需要用到mice函數，這個函數接受的引數如下：

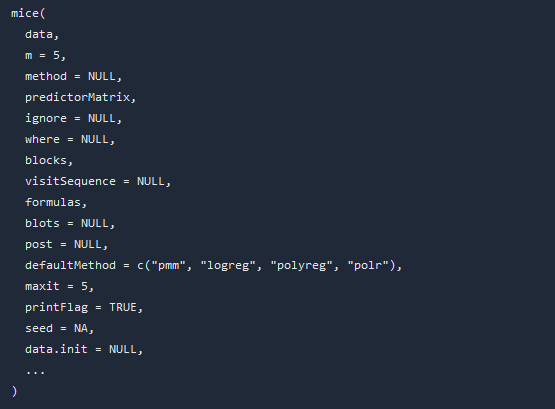
其中重要的引數包括m，就是插補的完整資料集的個數；method就是插補的演演算法，這個就比較多了，常見如下：

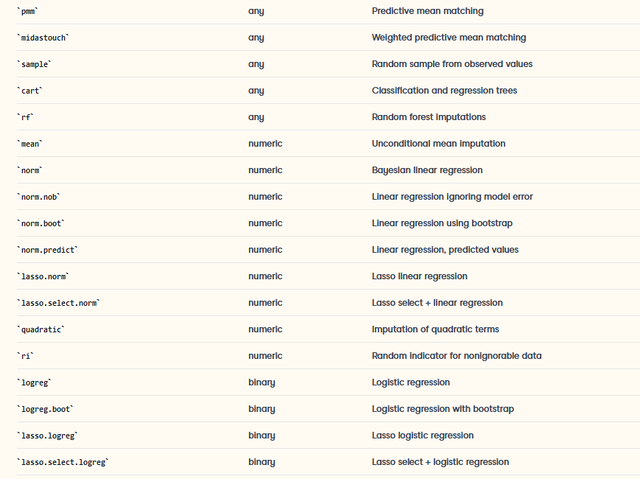
例如，我想對原始資料用pmm法進行多重插補，可以寫出程式碼如下：

imputed_data <- mice::mice(data, m = 25, method = "pmm", 
                           maxit = 10, seed = 12345, print = FALSE)

執行上面程式碼插補自動完成，我們可以看到

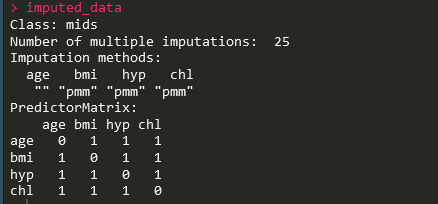
每一個變數都會作為其他變數的預測因子，同時每一個變數都會被其餘所有變數所預測從而完成插補。插補完成後我們可以檢視插補後的資料集，程式碼如下：

complete(imputed_data, action = "long", include = TRUE)

最重要的一步是進行分析並進行效應合併，這個需要用到mice包中的with函數，可不是base包中的with函數，這個需要注意

這個with是專門用來幫助我們在插補後的資料集中目標分析的函數，剛剛寫到我的目標分析是要做一個以hyp為因變數的邏輯迴歸，此時對於插補後的資料，可以寫出程式碼如下：

imputed_model <- with(imputed_data, 
                      glm(hyp ~ bmi+age+chl, family = binomial(link = 'logit')))

得到結果如下：

上圖中上面是插補後的邏輯迴歸的結果，下圖是之前沒有插補的時候邏輯迴歸的結果，可以看到差異還是蠻大的。

多重插補的報告

對於多重插補的結果報告，BMJ也給了指南：

完整文章如下，大家可以自己去閱讀：

Sterne J A C, White I R, Carlin J B, Spratt M, Royston P, Kenward M G et al. Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls BMJ 2009; 338 :b2393 doi:10.1136/bmj.b2393

其中的重點就是要報告用的啥軟體進行的多重插補，補了幾個資料集，補的時候用了哪些變數，非正態分佈變數和分類變數用的什麼method補的，如果目標分析有互動，補的時候考慮互動沒有；補的資料如果 太多，補與不補的個案需要對比的；還有建議對缺失機制做一個討論。

以上就是今天給大家介紹的多重插補的內容。