紙牌博弈問題

作者：Grey

原文地址：

題目描述

有一個整型陣列 A，代表數值不同的紙牌排成一條線。玩家 a 和玩家 b 依次拿走每張紙牌，
規定玩家 a 先拿，玩家 b 後拿，
但是每個玩家每次只能拿走最左或最右的紙牌，
玩家 a 和玩家 b 都絕頂聰明，他們總會採用最優策略。
請返回最後獲勝者的分數。

注：給定紙牌序列 A 及序列的大小 n，請返回最後分數較高者得分數(相同則返回任意一個分數)。保證 A 中的元素均小於等於1000。且 A 的大小小於等於300。

題目連結：牛客-紙牌博弈

暴力遞迴解

定義兩個遞迴函數，第一個遞迴函數是

int first(int[] A, int n, int start, int end)

這個遞迴函數表示的含義是：先手在陣列 A 的 start 到 end 範圍內，經過 n 輪，能獲得的最大的分數是多少。

base case 是，當 start == end 的時候，即陣列 A 只有一個元素，此時先手直接拿走這個元素，最大分數就是此時先手拿走的唯一元素值，即

        if (start == end) {
            return A[start];
        }

第二個遞迴函數是

int second(int[] A, int n, int start, int end)

這個遞迴函數表示的含義是：後手在陣列 A 的 start 到 end 範圍內，經過 n 輪，能獲得的最大的分數是多少。

base case 是，當 start == end 的時候，即陣列 A 只有一個元素，此時這個元素肯定要被先手拿走，那麼後手只能返回 0，即

        if (start == end) {
            return 0;
        }

接下來是普遍情況，對於先手函數來說，有兩個位置可以選，一個是 start 位置，另外一個是 end 位置，如果選了 start 位置，那麼先手在下一輪就是後手，即

A[start] + second(A, n, start + 1, end)

同理，如果選 end 位置，先手在下一輪是後手，即

A[end] + second(A, n, start, end - 1)

先手函數在做上述兩個決策的過程中，一定要取最大值，即

Math.max(A[start] + second(A, n, start + 1, end), A[end] + second(A, n, start, end - 1));

所以，先手函數的完整程式碼如下

    public static int first(int[] A, int n, int start, int end) {
        if (start == end) {
            return A[start];
        }
        return Math.max(A[start] + second(A, n, start + 1, end), A[end] + second(A, n, start, end - 1));
    }

接下來是後手函數的普遍情況，對於後手函數來說，沒有先選的權力，只能讓先手選完自己才能選，先手如果選了 start 位置，後手面對的選擇是

first(A, n, start + 1, end)

先手如果選了 end 位置，後手面對的選擇就是

first(A, n, start, end - 1)

後手在下一輪就是先手，所以要保證先手的上述選擇最小，即

Math.min(first(A, n, start + 1, end), first(A, n, start, end - 1));

定義了先手函數和後手函數，主函數做如下呼叫即可

    public static int cardGame(int[] A, int n) {
        // 沒有元素，直接返回0分
        if (n == 0) {
            return 0;
        }
        // 只有一個元素，無論如何，只能得到 A[0] 分
        if (n == 1) {
            return A[0];
        }
        // 只有兩個元素，選最大的那個
        if (n == 2) {
            return Math.max(A[0], A[1]);
        }
        // 普遍情況：先手後手中最大的那個
        return Math.max(first(A, n, 0, A.length - 1), second(A, n, 0, A.length - 1));
    }

超時

動態規劃解

根據上述暴力遞迴函數可知，兩個遞迴函數都可變引數都是 2 個，且可變引數的變化範圍是固定的，所以我們可以用兩個二維陣列來分別表示兩個遞迴函數的結果，

// 儲存先手函數的遞迴過程解
int[][] firstMap = new int[n][n];
// 儲存後手函數的遞迴過程解
int[][] secondMap = new int[n][n];

由於遞迴過程的兩個可變引數 start 和 end 是有範圍的，且 start 不可能大於 end，所以，上述兩個二維陣列的左下半區都是無效區域，無需考慮。

在暴力遞迴過程中，當 start == end 的時候，返回 A[start] 值，所以，針對 firstMap，其對角線（start == end）的值都是確定的

        // 對角線
        for (int i = 0; i < n; i++) {
            firstMap[i][i] = A[i];
        }

經過上述過程，可以得到兩個二維陣列的如下區域的內容

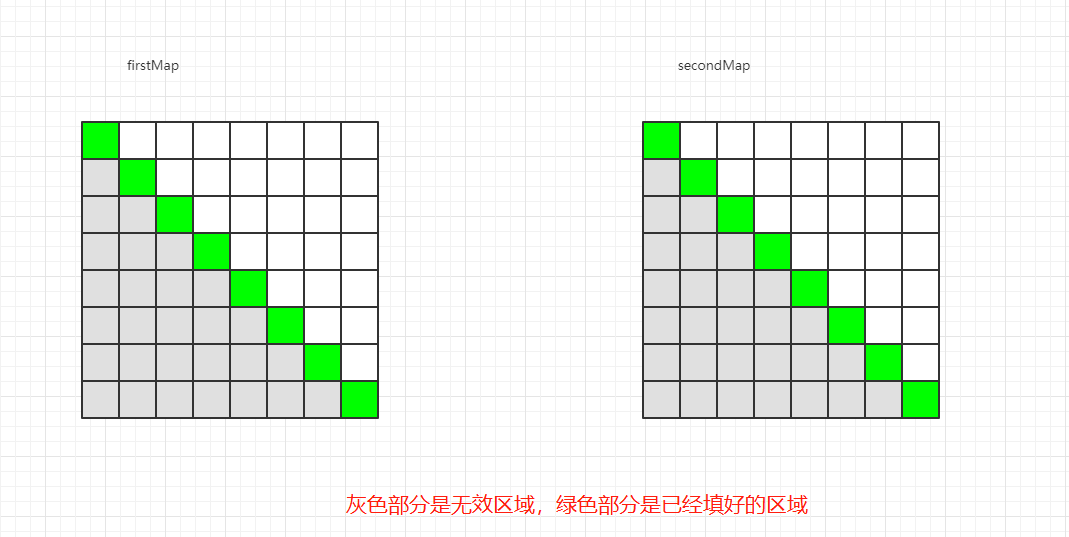
接下來就是普遍情況，

基於暴力遞迴過程可以很方便得到兩個二維陣列之間的遞推關係

        // 對角線下班區域不用管
        // 對角線上半區域
        for (int i = 1; i < n; i++) {
            int r = 0;
            int c = i;
            while (c < n) {
                firstMap[r][c] = Math.max(A[r] + secondMap[r + 1][c], A[c] + secondMap[r][c - 1]);
                secondMap[r][c] = Math.min(firstMap[r + 1][c], firstMap[r][c - 1]);
                r++;
                c++;
            }
        }

完整程式碼如下

import java.util.*;

public class Cards {

    public static int cardGame(int[] A, int n) {
        if (n == 0) {
            return 0;
        }
        if (n == 1) {
            return A[0];
        }
        if (n == 2) {
            return Math.max(A[0], A[1]);
        }
        int[][] firstMap = new int[n][n];
        int[][] secondMap = new int[n][n];
        // 對角線
        for (int i = 0; i < n; i++) {
            firstMap[i][i] = A[i];
        }
        // 對角線下班區域不用管
        // 對角線上半區域
        for (int i = 1; i < n; i++) {
            int r = 0;
            int c = i;
            while (c < n) {
                firstMap[r][c] = Math.max(A[r] + secondMap[r + 1][c], A[c] + secondMap[r][c - 1]);
                secondMap[r][c] = Math.min(firstMap[r + 1][c], firstMap[r][c - 1]);
                r++;
                c++;
            }
        }
        return Math.max(firstMap[0][n - 1], secondMap[0][n - 1]);
    }
}

演演算法和資料結構筆記

紙牌博弈問題

紙牌博弈問題

題目描述

暴力遞迴解

動態規劃解

更多