謠言檢測(RDCL)——《Towards Robust False Information Detection on Social Networks with Contrastive Learning
論文資訊
論文標題:Towards Robust False Information Detection on Social Networks with Contrastive Learning
論文作者:Chunyuan Yuan, Qianwen Ma, Wei Zhou, Jizhong Han, Songlin Hu
論文來源:2019,CIKM
論文地址:download
論文程式碼:download
1 Introduction
問題:對談圖中輕微的擾動講導致現有模型的預測崩潰。

研究了兩大類資料增強策略(破壞對談圖結構):
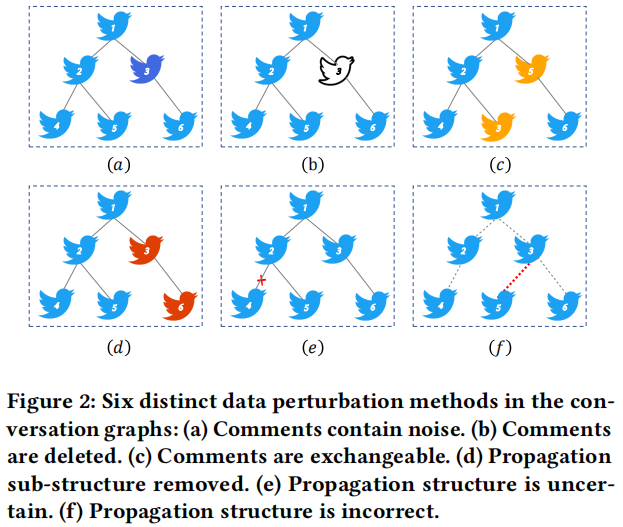
貢獻:
(1) 提出了RDCL框架,為虛假資訊檢測提供了魯棒的檢測結果,該框架利用對比學習從多個角度提高了模型對擾動訊號的感知。
(2) 證明了硬正樣本對可以提高對比學習的效果。
(3) 提出了一種有效的硬樣本對生成方法 HPG,它可以增加對比學習的效果,使模型學習更魯棒的表示。
(4) 通過比較實驗、在不同的 GNN 和兩個資料集上進行的消融實驗,證明了該模型的有效性。
2 Methodlogy
問題定義:預測無向對談圖的標籤。
整體框架如下:
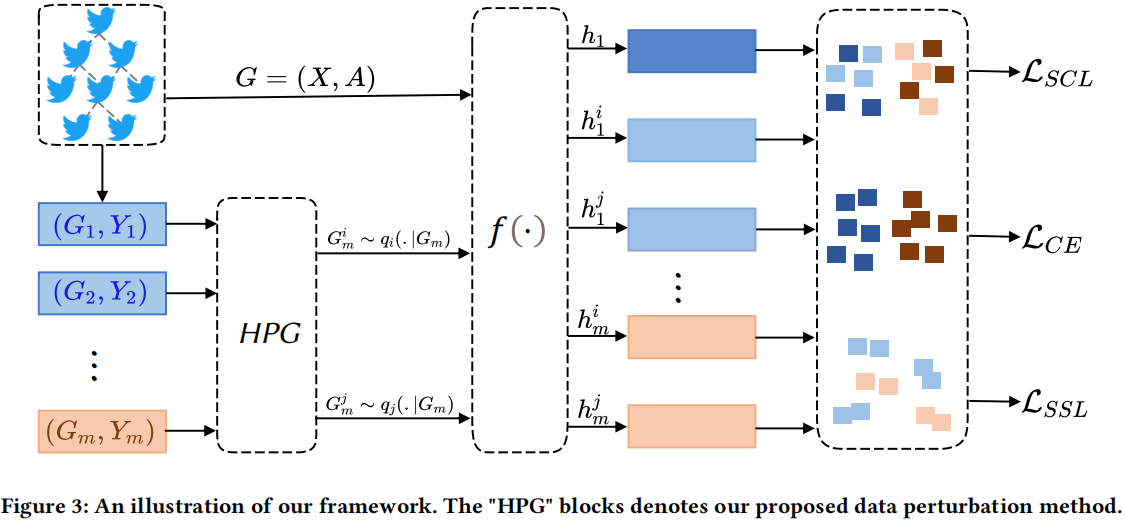
2.1 Data Perturbations
在除根節點以外的節點中,以 $\rho $ 的取樣率取樣節點,對於取樣的節點用高斯分佈初始化,沒有被取樣到的節點採用 0 填充:
$X_{C N}^{-r}=X^{-r}+X_{G a u s s i o n}^{-r}$
Comments are deleted (CD)
在除根節點以外的節點中,以 $\rho $ 的取樣率取樣節點,然後將其節點特徵向量置 0 :
$X_{C D}^{-r}=X^{-r} \odot D^{-r}$
Comments are exchangeable (CE)
在除根節點以外的節點中,以 $\rho $ 的取樣率取樣節點,交換節點特徵向量。
Propagation sub-structure is removed (PR)
在除根節點以外的節點中,隨機選擇一部分節點,並刪除其形成的子圖。
以 $\rho $ 的取樣率取樣邊,並刪除邊:
$A_{P U}=A-A_{\text {drop }}$
隨機選擇兩個節點 $C_i$ 和 $C_j$,對於 節點 $C_i$,選擇刪除它和它父節點之間的邊,並新增 $C_j$ 和 $C_i$ 之間的邊。
2.2 Contrastive Perturbation Learning
假設:對於含有相同標籤的圖,將他們認為是正樣本對,每個 batch 中有 $P$ 張圖,加上資料增強後生成的 $2P$ 張圖,總共有 $3P$ 張圖,自監督對比損失如下:
${\large \mathcal{L}_{S C L}=-\frac{1}{3 P} \log \frac{\sum\limits _{Y_{s}=Y_{m}} \exp \left(z_{m} \cdot z_{s} / \tau\right)}{\sum\limits_{Y_{s}=Y_{m}} \exp \left(z_{m} \cdot z_{s} / \tau\right)+\sum\limits_{Y_{d} \neq Y_{m}} \exp \left(z_{m} \cdot z_{d} / \tau\right)}} $
[ Anchor 和 資料增強圖之間的對比損失]
2.3 Perturbation Sample Pairs Generation
自監督損失:
$\begin{aligned}\mathcal{L}_{\mathrm{SSL}}=&-z_{m}^{i} \cdot z_{m}^{j} / \tau +\log \left(\exp \left(z_{m}^{i} \cdot z_{m}^{j} / \tau\right)+\sum\limits_{\mathrm{Neg}} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right)\right)\end{aligned}$
[資料增強圖之間的對比損失]
上述 $\mathcal{L}_{\text {SSL }}$ 關於 $z_{m}^{i}$ 的梯度為:
$\begin{aligned}\frac{\partial \mathcal{L}_{S S L}}{\partial z_{m}^{i}} &=-\frac{1}{\tau}\left(z_{m}^{j}-\frac{\exp \left(z_{m}^{i} \cdot z_{m}^{j} / \tau\right) z_{m}^{j}+\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right) z_{n e g}}{\exp \left(z_{m}^{i} \cdot z_{m}^{j} / \tau\right)+\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right)}\right) \\&=-\frac{\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right)\left(z_{m}^{j}-z_{m}^{i}\right)-\left(z_{n e g}-z_{m}^{i}\right)}{\tau \exp \left(z_{m}^{i} \cdot z_{m}^{j} / \tau\right)+\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g}\right) / \tau} \\&=-\frac{1}{C_{1} \tau}\left(\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right)\left(z_{m}^{j}-z_{m}^{i}\right)+C_{2}\right)\end{aligned}$
其中:
$C_{1}=\exp \left(z_{m}^{i} \cdot z_{m}^{j} / \tau\right)+\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right)$
$C_{2}=z_{n e g}-z_{m}^{i}$
$\text{Eq.7}$ 在分子中的梯度貢獻主要來自於($z_{m}^{j}-z_{m}^{i}$)。因此,如果能夠增加圖級空間中樣本對之間的距離,它將提供更大的梯度訊號,從而增加模型的學習難度,提高對比學習的質量。所以,本文的對比檢視生成方法如下:

Figure 5 說明,由 HPG 生成的資料增強圖,他們之間的相似度小於其他資料增強方法,那麼損失函數 SSL 會加大對模型的懲罰,提高對比學習的質量。

雖然擾動會加大學習的難度,但是他們提供了足夠的資訊去儲存檢視之間的一致性。
2.4 Training Objective
3 Experiment
3.1 Datasets
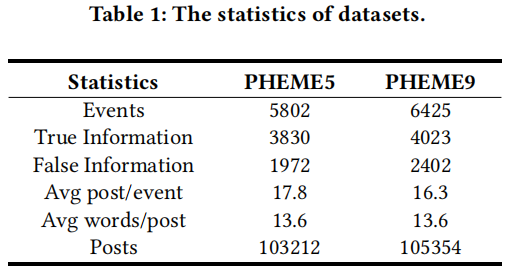
3.2 Performance Comparison

3.3 Robustness Studies
基於本文的 6 中資料增強策略,對比 GACL 和本文方法:

3.4 The robustness on different perturbation scenarios
研究採用複雜資料增強策略組合的對比實驗:

3.5 Ablation Studies
研究如下 6 中資料增強策略 Node Mask , Edge Drop , Mixed , Node-based, Topology-based and our method HPG 的實驗對比結果:


3.6 Graph-level Representation Studies

3.7 The Impact of Perturbation Probability $\rho$
不同擾動率 和 不同編碼器的實驗對比:

因上求緣,果上努力~~~~ 作者:視界~,轉載請註明原文連結:https://www.cnblogs.com/BlairGrowing/p/16846443.html