小樣本利器4. 正則化+資料增強 Mixup Family程式碼實現

前三章我們陸續介紹了半監督和對抗訓練的方案來提高模型在樣本外的泛化能力，這一章我們介紹一種嵌入模型的資料增強方案。之前沒太重視這種方案，實在是方法過於樸實。。。不過在最近用的幾個資料集上mixup的表現都比較哇塞，所以我們再來聊聊~

Mixup

paper: mixup: Beyond Empirical Risk Minimization

TF原始碼：https://github.com/facebookresearch/mixup-cifar10

torch復現：ClassicSolution

原理

mixup的實現非常簡單，它從訓練集中隨機選擇兩個樣本，對x和y分別進行線性加權，使用融合後的\(\tilde{x}, \tilde{y}\)進行模型訓練

\[\tilde{x} = \lambda x_i + (1-\lambda) x_j \\ \tilde{y} = \lambda y_i + (1-\lambda) y_j \]

對x的融合比較容易理解，例如針對影象輸入，mixup對輸入特徵層的線性融合可以被直觀的展現如下。

對y的融合，如果是2分類問題且\(\lambda=0.3\), 一個y=1的樣本融合一個y=0的樣本後d得到\(\tilde{y}=[0.3,0.7]\)，等價於兩個樣本損失函數的線性加權，既0.3 *CrossEntropy(y=0)+0.7 * CrossEntropy(y=1)

如何理解mixup會生效呢？作者是從資料增強的角度給出瞭解釋，認為線性差值的方式拓展了訓練集覆蓋的區域，在原始樣本未覆蓋區域（in-between area）上讓模型學到一個簡單的label線性差值的結果，從而提高模型樣本外的泛化效果~

不過我更傾向於從正則化的角度來理解，因為模型並不是在原始樣本上補充差值樣本進行訓練，而是完全使用差值樣本進行訓練。線性差值本身是基於一個簡化的空間假設，既輸入的線性加權可以對映到輸出的線性加權。這個簡化的假設會作為先驗資訊對模型學習起到正則約束的作用，使得模型的分類邊界更加平滑，且分類邊界離樣本高密度區更遠。這和我們上一章提到的半監督3大假設，平滑性假設，低密度分離假設相互呼應~

作者對比了原模型和mixup增強模型在對抗樣本上的預測誤差，驗證了mixup可以有效提高模型在擾動樣本上的魯棒性，不過看誤差感覺對抗訓練可能可以和mixup並行使用，以後有機會嘗試後再來補充~

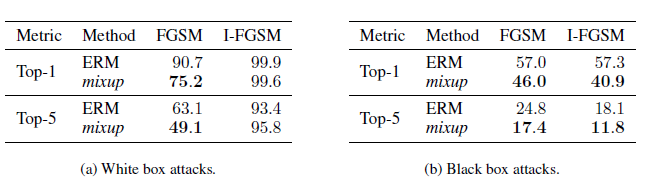
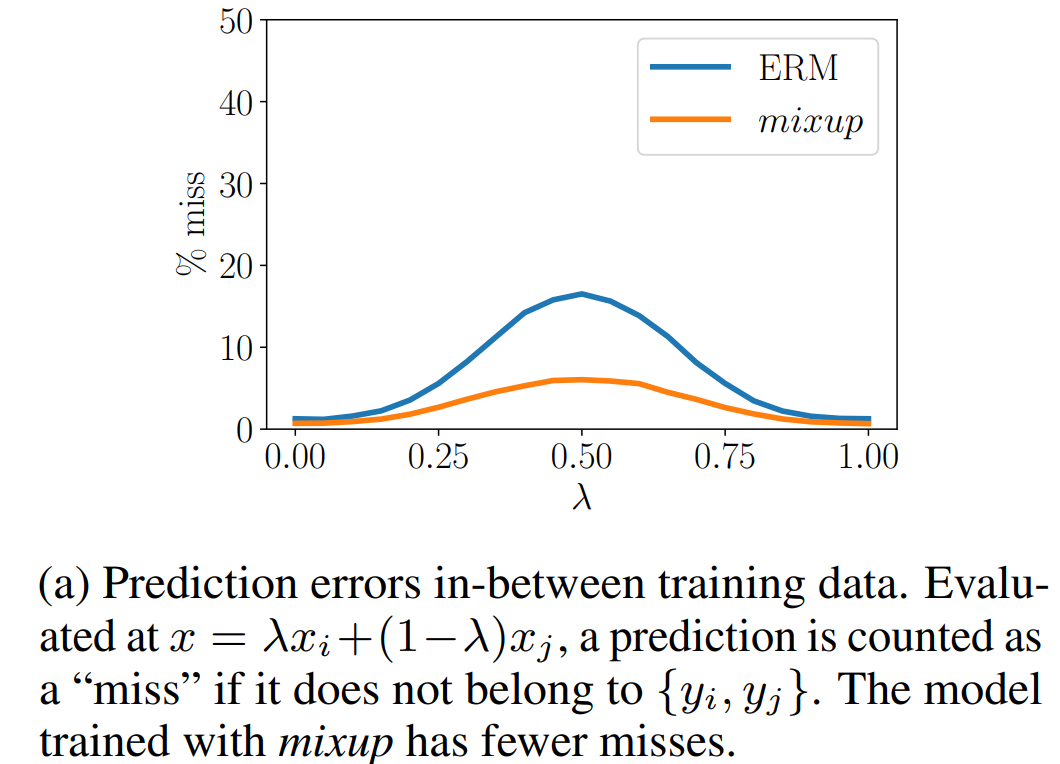
同時作者做了個有趣的實驗，對比了在融合樣本上的預測誤差，舉個栗子0.3個體育新聞融合0.7個娛樂新聞讓模型去做預測，如果預測結果既非體育也非娛樂則判斷為miss。下圖顯示mixup可以有效降低miss率。間接作證了mixup有提高in-between樣本外預測的效果~

實際應用中還有幾個細節有待討論

在哪一層進行mixup效果更好

作者在影象分類任務中對比了layer1~6，最終發現對最底層施加mixup的效果最好。和FGM一樣，如果對高層進行mixup，因為非線性程度較低，可能會導致模型欠擬合

只在同一個類別內部進行mixup還是對全類別進行隨機mixup

作者對比了類內mixup，和所有類隨機mixup，效果是隨機mixup效果更好。感覺不限制插值類別才是保證分類邊界遠離樣本高密度區的關鍵，因為mixup會使得模型在兩個分類cluster中間未覆蓋的區域學到一個線性插值的分類，從而使得分類邊界遠離任意類別樣本的覆蓋區域

是否需要限制mixup樣本之間的相似度，避免引入過多噪聲
作者嘗試把mixup的範圍限制在KNN200，不過效果沒有隨機mixup效果好
混合權重的選擇
論文並沒有對應該如何選擇插值的權重給出太多的建議，實際嘗試中我也一般是從大往小了調，在一些小樣本上如果權重太大會明顯看到模型欠擬合，這時再考慮適當調低權重，和dropout擾動相同權重越大正則化效果越強，也就越容易欠擬合

實現

def mixup(input_x, input_y, label_size, alpha):
    # get mixup lambda
    batch_size = tf.shape(input_x)[0]
    input_y = tf.one_hot(input_y, depth=label_size)

    mix = tf.distributions.Beta(alpha, alpha).sample(1)
    mix = tf.maximum(mix, 1 - mix)

    # get random shuffle sample
    index = tf.random_shuffle(tf.range(batch_size))
    random_x = tf.gather(input_x, index)
    random_y = tf.gather(input_y, index)

    # get mixed input
    xmix = input_x * mix + random_x * (1 - mix)
    ymix = tf.cast(input_y, tf.float32) * mix + tf.cast(random_y, tf.float32) * (1 - mix)
    return xmix, ymix

Pytorch的實現如下

class Mixup(nn.Module):
    def __init__(self, label_size, alpha):
        super(Mixup, self).__init__()
        self.label_size = label_size
        self.alpha = alpha

    def forward(self, input_x, input_y):
        if not self.training:
            return input_x, input_y
        batch_size = input_x.size()[0]
        input_y = F.one_hot(input_y, num_classes=self.label_size)

        # get mix ratio
        mix = np.random.beta(self.alpha, self.alpha)
        mix = np.max([mix, 1 - mix])

        # get random shuffle sample
        index = torch.randperm(batch_size)
        random_x = input_x[index, :]
        random_y = input_y[index, :]

        xmix = input_x * mix + random_x * (1 - mix)
        ymix = input_y * mix + random_y * (1 - mix)
        return xmix, ymix

遷移到NLP場景

paper: Augmenting Data with mixup for Sentence Classification: An Empirical Study

mixup的方案是在CV中提出，那如何遷移到NLP呢？其實還是在哪一層進行差值的問題，在NLP中一般可以在兩個位置進行融合，在過Encoder之前對詞向量融合，過Encoder之後對句向量進行融合。

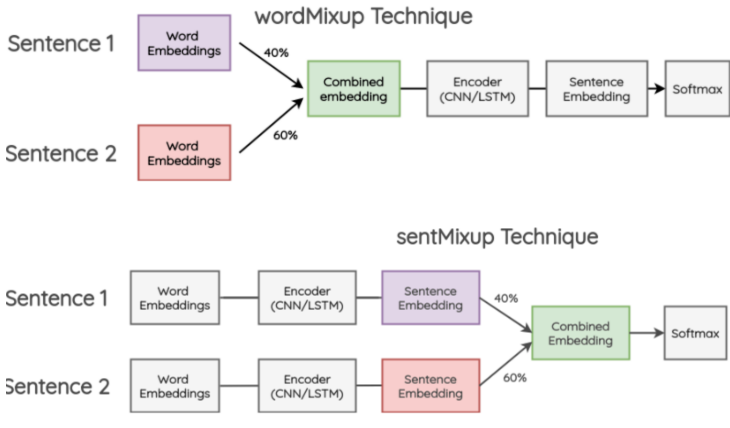
作者在文字分類任務上對比了二者的效果，並嘗試了隨機詞vs預訓練詞向量 * 允許微調vs凍結詞向量，總共4種不同的情況。整體上不論是wordmixup還是sentmixup都對效果有一定提升，不過二者的差異並不如以上的CV實驗中顯著。

在[應用類別識別挑戰賽](https://challenge.xfyun.cn/topic/info?type=scene-division)中，我分別嘗試了FGM，Temporal半監督，文字增強，和mixup來提升文字分類模型的效果。在我使用的詞+字向量的TextCNN模型結構中，mixup的表現最好，單模型在初賽排到13名。之後等Top3解決方案出來後，我們再來總結這個比賽~

Manifold Mixup

paper: Manifold Mixup: Better Representations by Interpolating Hidden States

github: https://github.com/vikasverma1077/manifold_mixup

Manifold Mixup是在mixup基礎上的改良，一言以蔽之就是把上面糾結的mixup在哪一層進行插值的問題，變成了每個step都隨機選一層進行插值。個人很喜歡這篇paper有兩個原因，其一是因為覺得作者對mixup為何有效比原作解釋的更加簡單易懂；其二是它對插值位置的選擇方案更適合BERT這類多層Encoder的模型。而反觀cv場景，優化點更多集中在cutmix這類對插值資訊（對兩個畫素框內的資訊進行融合）的選擇上，核心也是因為影象輸入的畫素的資訊量要遠小於文字輸入的字元所包含的資訊量。

說回Manifold mixup，它的整體實現方案很簡單:在個layer中任選一個layer K，這裡包括輸入層(layer=0), 然後向前傳導到k層進行mixup就齊活了。作者的程式碼實現也很簡單一個randint做層數選擇，加上一連串的if layer==i則進行mixup就搞定了~

關鍵我們來拜讀下作者對於Manifold Mixup為何有效的解釋，作者從空間表徵上給出了3個觀點

得到更平滑，且遠離樣本覆蓋空間的決策邊界，這個同mixup
展平分類的空間表徵：啥叫展平這個我最初也木有看懂，不過作者的證明方式更加易懂，作者對比了不同的正則方案mixup，dropout，batchnorm和manifold對隱藏層奇異值的影響，發現manifold相較其他正則化可以有效降低隱藏層的整體奇異值。降低奇異值有啥用嘞？簡單說就是一個矩陣越奇異，則越少的奇異值蘊含了更多的矩陣資訊，矩陣的資訊熵越小。所以這裡作者認為mixup起到了降低預測置信度從而提高泛化的作用。更詳細對奇異值的解釋可以去知乎膜拜各路大神的奇異值的物理意義是什麼？
更高隱藏層的融合，提供更多的訓練訊號：個人閱讀理解給出的解讀是高層的空間表徵更貼近任務本身，因此融合帶來的增益更大。這也是我之前對為啥文字任務在Encoder之後融合效果效果有時比在輸入層融合還要好的強行解釋。。。。

至於Manifold mixup為何比mixup更好，作者做了更多的數學證明，不過。。。這個大家感興趣去看下就知道這裡為何省略一萬字了~以及之後出現的Flow Mixup也挑戰過Manifold會導致樣本分佈飄逸以及訓練不穩定的問題，不過我並沒有在NLP上嘗試過manifold的方案，以後要是用了再來comment ~