【影象處理筆記】影象分割之聚類和超畫素
0 引言
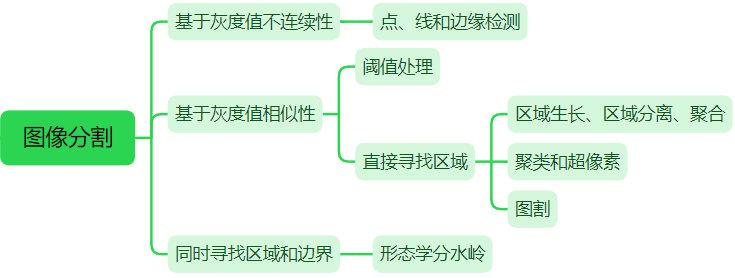
大多數分割演演算法都基於影象灰度值的兩個基本性質之一:不連續性和相似性。第一類方法根據灰度的突變(如邊緣)將影象分割為多個區域:首先尋找邊緣線段,然後將這些線段連線為邊界的方法來識別區域。第二類方法根據一組預定義的準則把一幅影象分割為多個區域。本節討論兩種相關的區域分割方法:(1)在資料中尋找聚類的經典方法,它與亮度和顏色等變數有關;(2)用聚類從影象中提取「超畫素」的現代方法。
1 使用k均值聚類的區域分割
1.1 原理
聚類方法的思想是將樣本集合按照其特徵的相似性劃分為若干類別,使同一類別樣本的特徵具有較高的相似性,不同類別樣本的特徵具有較大的差異性。令{z1, z2, z3 ..., zn}是樣本集合,在影象分割中,樣本向量z的每個分量表示一個數值畫素屬性。例如,分割只基於灰度尺度時,z是一個表示畫素灰度的標量。分割的如果是RGB彩色影象,z通常是一個三維向量,這個三維向量的每個分量是RGB三通道的灰度值。k均值聚類的目的就是將樣本集合劃分為k個滿足如下最優準則的不相交的聚類集合C={C1, C2, ..., Ck}:

式中,mi是集合Ci中樣本的均值向量(或質心),||z-mi||項是Ci中的一個樣本到均值mi的歐式距離。換言之,這個公式說,我們感興趣的是找到集合C={C1, C2, ..., Ck},集合中的每個點到該集合的均值的距離之和是最小的。
基於聚類的區域分割,就是基於影象的灰度、顏色、紋理、形狀等特徵,用聚類演演算法把影象分成若干類別或區域,使每個點到聚類中心的均值最小。k 均值(k-means)是一種無監督聚類演演算法。基於 k 均值聚類演演算法的區域分割,演演算法步驟為:
(1)初始化演演算法:規定一組初始均值
(2)將樣本分配給聚類:對所有的畫素點,計算畫素到每個聚類中心的距離,將畫素分類到距離最小的一個聚類中;
(3)更新聚類中心:根據分類結果計算出新的聚類中心;
(4)完備性驗證:計算當前步驟和前幾步中平均向量之間的差的歐幾里得範數。計算殘差E,即k個範數之和。若E≤T,其中T是一個規定的非負閾值,則停止。否則,返回步驟2。
1.2 cv::kmeans函數
OpenCV提供了函數cv::kmeans來實現 k-means 聚類演演算法。函數cv::kmeans不僅可以基於灰度、顏色對影象進行區域分割,也可以基於樣本的其它特徵如紋理、形狀進行聚類。
double cv::kmeans(InputArray data, //用於聚類的資料,型別為 CV_32F int K, //設定的聚類數量 InputOutputArray bestLabels, //輸出整數陣列,用於儲存每個樣本的聚類類別索引 TermCriteria criteria, //演演算法終止條件:即最大迭代次數或所需精度 int attempts, //用於指定使用不同初始標記執行演演算法的次數 int flags, //初始化聚類中心的方法:0=隨機初始化 1=kmeans++方法初始化 2=第一次用使用者指定的標籤初始化,後面attempts-1都用隨機或版隨機的初始化 OutputArray centers = noArray() //聚類中心的輸出矩陣,每個聚類中心佔一行 )
範例 影象分割之k均值聚類
Mat src = imread("./14.tif", 0);
Mat dataPixels = src.reshape(0, 1);//可以是一列,每一行表示一個樣本;或者一行,一列是一個樣本;樣本的分量數為通道數
dataPixels.convertTo(dataPixels, CV_32FC1);//輸入需要是32位元浮點型
int numCluster = 3;
Mat labels;
Mat centers;
kmeans(dataPixels, numCluster, labels, TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 10, 0.1), 3, KMEANS_PP_CENTERS, centers);
Mat dst = Mat::zeros(src.size(), CV_8UC1);
float* pdata = dataPixels.ptr<float>(0);
for (int i = 0; i < src.rows * src.cols; i++) {
int k = labels.ptr<int>(i)[0];//每個畫素對應的標籤k,即屬於集合k
pdata[i] = centers.ptr<float>(k)[0];//用集合中心替換該畫素
}
dataPixels.convertTo(dataPixels, CV_8UC1);
dst = dataPixels.reshape(0, src.rows);

1.3 cv::kmeans原始碼
當圖片非常大時,對影象進行簡單的計算操作,耗時就會變得非常大,常用的加速方法如OpenMp,TBB,OpenCL和CUDA。使用cuda時,圖片在cpu和gpu之間的傳輸時間就達到上百ms,不適合本來就是ms級的計算。在kmeans原始碼中使用parallel_for_平行計算各個樣本到聚類中心的距離。這邊寫一個簡單的例子,瞭解下parallel_for_的用法。
範例 利用平行計算加速圖片旋轉
// 方法1:並行 將該方法寫成一個類,繼承ParallelLoopBody,然後重寫(),利用parallel_for_可以開啟並行
class trans :public ParallelLoopBody {
public:
trans(const uchar* _src, uchar*_dst, int _dims, int _istep):src(_src), dst(_dst), dims(_dims), istep(_istep) {}
void operator()(const Range& range) const //過載操作符()
{
for (int n = range.start; n < range.end; ++n)
{
for (int i = 0; i < dims; i++)
dst[i * istep + (istep - 1 - n)] = src[n * dims + i];
}
}
private:
const uchar* src;
uchar* dst;
int dims;
int istep;
};
// 方法2 for迴圈
void rotate(Mat& src, Mat& dst, int srcWidth, int srcHeight)
{
int istep = src.step;
uchar* psrc = src.ptr<uchar>();
uchar* pdst = dst.ptr<uchar>();
for (size_t i = 0; i < srcHeight; i++)
for (size_t j = 0; j < srcWidth; j++)
pdst[j * istep + (istep-1-i)] = psrc[i * istep + j];
}
//呼叫
uchar* psrc = src.ptr<uchar>();
uchar* pdst = dst.ptr<uchar>();
int dims = src.cols;
int istep = src.step;
int N = src.rows;
rotate(src, dst, ROTATE_90_CLOCKWISE);// opencv提供的方法 3ms
rotate(src, dst, src.cols, src.rows);// 自己寫的for迴圈 20ms
parallel_for_(Range(0, N), trans(psrc, pdst, dims, istep)); // 並行加速3ms
原始碼位於opencv路徑下sources\modules\core\src\kmeans.cpp中,首先是初始化演演算法:規定一組初始center,一種是隨機產生,另一種是用kmeans++初始化。kmeans++初始化聚類中心是以概率的形式逐個選擇聚類中心,並在選擇聚類中心時,給距離較遠的點更高的權重,即更容易被選擇為聚類中心。假設有5個點,隨機選擇其中一個點為中心,計算其他點到該點的距離的平方分別為10,20,5,15。則選下一個聚類中心時它們的權值為0.2,0.4,0.1和0.3。用程式碼寫就是,距離平方和50,在【0,50】間隨機生成一個數,用這個數挨個減去10,再減去20...直到結果小於0,下一個聚類中心就是該點。
// 隨機產生聚類中心
// dims 樣本向量的分量數
// box 存放了所有樣本中每個分量的最大值和最小值
static void generateRandomCenter(int dims, const Vec2f* box, float* center, RNG& rng)
{
float margin = 1.f / dims;
for (int j = 0; j < dims; j++)
center[j] = ((float)rng * (1.f + margin * 2.f) - margin) * (box[j][1] - box[j][0]) + box[j][0];
}
/*
k-means center initialization using the following algorithm:
Arthur & Vassilvitskii (2007) k-means++: The Advantages of Careful Seeding
*/
static void generateCentersPP(const Mat& data, Mat& _out_centers,
int K, RNG& rng, int trials)
{
CV_TRACE_FUNCTION();
const int dims = data.cols, N = data.rows;
cv::AutoBuffer<int, 64> _centers(K);
int* centers = &_centers[0];
cv::AutoBuffer<float, 0> _dist(N * 3);// 3倍樣本數量大小,存不同時刻樣本到最近聚類中心的距離
float* dist = &_dist[0], * tdist = dist + N, * tdist2 = tdist + N;
double sum0 = 0;
// 第一個聚類中心隨機生成
centers[0] = (unsigned)rng % N;// %N 即可獲得[0,N-1]的亂數
// 計算所有樣本到第一個中心的距離,並求和
for (int i = 0; i < N; i++)
{
dist[i] = hal::normL2Sqr_(data.ptr<float>(i), data.ptr<float>(centers[0]), dims);
sum0 += dist[i];
}
// 計算第2、3...個聚類中心,離第一個中心越遠的點權重越高
for (int k = 1; k < K; k++)
{
double bestSum = DBL_MAX;
int bestCenter = -1;
for (int j = 0; j < trials; j++)// 相當於隨機拋硬幣掉在哪個格子裡,做trials次
{
double p = (double)rng * sum0;//(double)rng會產生0-1的亂數
int ci = 0;
for (; ci < N - 1; ci++)
{
p -= dist[ci];
if (p <= 0)
break;
}
//選中第ci個樣本為聚類中心,計算距離,如果有樣本離新聚類中心更近,距離會被更新
parallel_for_(Range(0, N),
KMeansPPDistanceComputer(tdist2, data, dist, ci),
(double)divUp((size_t)(dims * N), CV_KMEANS_PARALLEL_GRANULARITY));
double s = 0;
for (int i = 0; i < N; i++)//所有樣本離其最近的聚類中心之和
{
s += tdist2[i];
}
if (s < bestSum)
{
bestSum = s;
bestCenter = ci;
std::swap(tdist, tdist2);// 把總和最小的資料暫存在tdist中
}
}
if (bestCenter < 0)
CV_Error(Error::StsNoConv, "kmeans: can't update cluster center (check input for huge or NaN values)");
centers[k] = bestCenter;
sum0 = bestSum;
std::swap(dist, tdist);// 把總和最小的資料從tdist放入dist
}
for (int k = 0; k < K; k++)// centers中存放的是聚類中心對應的樣本在樣本集合中的索引
{
const float* src = data.ptr<float>(centers[k]);
float* dst = _out_centers.ptr<float>(k);
for (int j = 0; j < dims; j++)
dst[j] = src[j];// 把k個聚類中心樣本放到_out_centers中
}
}
計算距離
// 平行計算每個樣本距離中心的距離
// dist 3倍樣本數量N的autobuffer,前N個存放上次的N個距離(dist_指向第一個),後N個存放本次計算的N個距離(tdist2_指向第一個)
// data 樣本向量集合
// ci 計算所有樣本和第ci個樣本的距離
class KMeansPPDistanceComputer : public ParallelLoopBody
{
public:
KMeansPPDistanceComputer(float* tdist2_, const Mat& data_, const float* dist_, int ci_) :
tdist2(tdist2_), data(data_), dist(dist_), ci(ci_)//成員初始化列表的寫法
{ }
void operator()(const cv::Range& range) const CV_OVERRIDE
{
CV_TRACE_FUNCTION();
const int begin = range.start;
const int end = range.end;
const int dims = data.cols;
for (int i = begin; i < end; i++)//遍歷每一行,一行為一個樣本向量,一個向量有dims個分量
{//需要計算的是每個樣本到離他最近的中心的距離,通過比較上一次dist中的距離和本次的tdist2哪個更小來實現
tdist2[i] = std::min(hal::normL2Sqr_(data.ptr<float>(i), data.ptr<float>(ci), dims), dist[i]);
}
}
private:
KMeansPPDistanceComputer& operator=(const KMeansPPDistanceComputer&); // = delete
float* tdist2;
const Mat& data;
const float* dist;
const int ci;
};
更新標籤
// 平行計算每個樣本到對應中心的距離,已知樣本屬於哪個集合,直接計算該樣本到集合中心的距離
template<bool onlyDistance>
class KMeansDistanceComputer : public ParallelLoopBody
{
public:
KMeansDistanceComputer(double* distances_,
int* labels_,
const Mat& data_,
const Mat& centers_)
: distances(distances_),
labels(labels_),
data(data_),
centers(centers_)
{
}
void operator()(const Range& range) const CV_OVERRIDE
{
CV_TRACE_FUNCTION();
const int begin = range.start;
const int end = range.end;
const int K = centers.rows;
const int dims = centers.cols;
for (int i = begin; i < end; ++i)
{
const float* sample = data.ptr<float>(i);
if (onlyDistance)// 只算距離,不重新分配標籤
{
const float* center = centers.ptr<float>(labels[i]);
distances[i] = hal::normL2Sqr_(sample, center, dims);
continue;
}
else // 遍歷每一個樣本,計算該樣本到每一箇中心的距離,重新分配標籤
{
int k_best = 0;
double min_dist = DBL_MAX;
for (int k = 0; k < K; k++)
{
const float* center = centers.ptr<float>(k);
const double dist = hal::normL2Sqr_(sample, center, dims);
if (min_dist > dist)
{
min_dist = dist;
k_best = k;
}
}
distances[i] = min_dist;
labels[i] = k_best;
}
}
}
private:
KMeansDistanceComputer& operator=(const KMeansDistanceComputer&); // = delete
double* distances;
int* labels;
const Mat& data;
const Mat& centers;
};
kmeans
//_data:特徵向量集;K:聚類中心個數;_bestLabels:每個特徵向量隸屬聚類中心索引
//criteria:迭代演演算法終止條件;attempts:嘗試次數;
//flags:第一次嘗試初始化採取策略;_centers:存放聚類中心
double cv::kmeans(InputArray _data, int K,
InputOutputArray _bestLabels,
TermCriteria criteria, int attempts,
int flags, OutputArray _centers)
{
CV_INSTRUMENT_REGION();
const int SPP_TRIALS = 3;
Mat data0 = _data.getMat();
const bool isrow = data0.rows == 1;// 輸入的資料應該是一行,或者一列的,通道數是每個樣本向量的分量數
const int N = isrow ? data0.cols : data0.rows;// N表示樣本向量個數
const int dims = (isrow ? 1 : data0.cols) * data0.channels();// 每個樣本向量的維度(分量數)
const int type = data0.depth();//資料型別,應為32位元浮點數
attempts = std::max(attempts, 1);//至少嘗試一次
CV_Assert(data0.dims <= 2 && type == CV_32F && K > 0);
CV_CheckGE(N, K, "Number of clusters should be more than number of elements");
Mat data(N, dims, CV_32F, data0.ptr(), isrow ? dims * sizeof(float) : static_cast<size_t>(data0.step));
_bestLabels.create(N, 1, CV_32S, -1, true);//_bestLabels為N*1大小矩陣,型別為32為有符號整型,每個樣本向量有有一個標籤
Mat _labels, best_labels = _bestLabels.getMat();
if (flags & CV_KMEANS_USE_INITIAL_LABELS) // 如果首次是由使用者指定的
{
CV_Assert((best_labels.cols == 1 || best_labels.rows == 1) &&
best_labels.cols * best_labels.rows == N &&
best_labels.type() == CV_32S &&
best_labels.isContinuous());
best_labels.reshape(1, N).copyTo(_labels);
for (int i = 0; i < N; i++)//將內容複製到_labels中
{
CV_Assert((unsigned)_labels.at<int>(i) < (unsigned)K);
}
}
else //否則,建立空的_labels
{
if (!((best_labels.cols == 1 || best_labels.rows == 1) &&
best_labels.cols * best_labels.rows == N &&
best_labels.type() == CV_32S &&
best_labels.isContinuous()))
{
_bestLabels.create(N, 1, CV_32S);
best_labels = _bestLabels.getMat();
}
_labels.create(best_labels.size(), best_labels.type());
}
int* labels = _labels.ptr<int>();
Mat centers(K, dims, type), old_centers(K, dims, type), temp(1, dims, type);
cv::AutoBuffer<int, 64> counters(K);
cv::AutoBuffer<double, 64> dists(N);
RNG& rng = theRNG();
if (criteria.type & TermCriteria::EPS)//演演算法精度
criteria.epsilon = std::max(criteria.epsilon, 0.);
else
criteria.epsilon = FLT_EPSILON;
criteria.epsilon *= criteria.epsilon;
if (criteria.type & TermCriteria::COUNT)//最大迭代次數
criteria.maxCount = std::min(std::max(criteria.maxCount, 2), 100);
else
criteria.maxCount = 100;
if (K == 1)
{
attempts = 1;
criteria.maxCount = 2;
}
cv::AutoBuffer<Vec2f, 64> box(dims);
if (!(flags & KMEANS_PP_CENTERS))//隨機初始化中心的話要計算下範圍,在最大小值之間隨機生成
{
{
const float* sample = data.ptr<float>(0);
for (int j = 0; j < dims; j++)
box[j] = Vec2f(sample[j], sample[j]);
}
for (int i = 1; i < N; i++)
{
const float* sample = data.ptr<float>(i);
for (int j = 0; j < dims; j++)
{
float v = sample[j];
box[j][0] = std::min(box[j][0], v);
box[j][1] = std::max(box[j][1], v);
}
}
}
double best_compactness = DBL_MAX;
for (int a = 0; a < attempts; a++)//演演算法嘗試次數為attempts次
{
double compactness = 0;
for (int iter = 0; ;)
{
double max_center_shift = iter == 0 ? DBL_MAX : 0.0;
swap(centers, old_centers);
//迴圈初始,需要對centers進行初始化操作,這裡主要是兩種,一個是random,另一個是kmeans++演演算法
if (iter == 0 && (a > 0 || !(flags & KMEANS_USE_INITIAL_LABELS)))
{
if (flags & KMEANS_PP_CENTERS)
generateCentersPP(data, centers, K, rng, SPP_TRIALS);
else
{
for (int k = 0; k < K; k++)
generateRandomCenter(dims, box.data(), centers.ptr<float>(k), rng);
}
}
else //若為人工指定labels,或者不是第一次迭代,將樣本劃分進不同的集合,根據labels
{
// compute centers
centers = Scalar(0); // 對centers進行初始化操作
for (int k = 0; k < K; k++)
counters[k] = 0;// 對counter進行初始化操作,統計每個集合包含樣本向量個數
for (int i = 0; i < N; i++)// 將樣本按照label分為k類,每一類計算樣本值的總和、樣本個數
{
const float* sample = data.ptr<float>(i);
int k = labels[i];
float* center = centers.ptr<float>(k);
for (int j = 0; j < dims; j++)
center[j] += sample[j];
counters[k]++;
}
for (int k = 0; k < K; k++)// 遍歷所有的集合,看有沒有空的集合
{
if (counters[k] != 0)
continue;
// if some cluster appeared to be empty then:
// 1. find the biggest cluster
// 2. find the farthest from the center point in the biggest cluster
// 3. exclude the farthest point from the biggest cluster and form a new 1-point cluster.
int max_k = 0;
for (int k1 = 1; k1 < K; k1++)// 1. 找最大的樣本集合(counters中存放每個集合的樣本數)
{
if (counters[max_k] < counters[k1])
max_k = k1;
}
double max_dist = 0;
int farthest_i = -1;
float* base_center = centers.ptr<float>(max_k);
float* _base_center = temp.ptr<float>(); // normalized
float scale = 1.f / counters[max_k];
for (int j = 0; j < dims; j++)
_base_center[j] = base_center[j] * scale;
for (int i = 0; i < N; i++)// 2. 找最大集合中離集合最遠的點
{
if (labels[i] != max_k)
continue;
const float* sample = data.ptr<float>(i);
double dist = hal::normL2Sqr_(sample, _base_center, dims);
if (max_dist <= dist)
{
max_dist = dist;
farthest_i = i;
}
}
// 3. 從最大集合中去掉這個最遠點,在空集合中加入該點
counters[max_k]--;
counters[k]++;
labels[farthest_i] = k;
const float* sample = data.ptr<float>(farthest_i);
float* cur_center = centers.ptr<float>(k);
for (int j = 0; j < dims; j++)
{
base_center[j] -= sample[j];//最大集合減去該樣本的值
cur_center[j] += sample[j];//空集合加上該樣本的值
}
}
for (int k = 0; k < K; k++)// 此時所有的集合都是有樣本的
{
float* center = centers.ptr<float>(k);
CV_Assert(counters[k] != 0);
float scale = 1.f / counters[k];
for (int j = 0; j < dims; j++)// center中是樣本值的和,除以樣本數量等於聚類中心
center[j] *= scale;
if (iter > 0)// 計算本次迴圈和上次聚類中心的差距,差距小於criteria.epsilon則為最後一次迭代
{
double dist = 0;
const float* old_center = old_centers.ptr<float>(k);
for (int j = 0; j < dims; j++)
{
double t = center[j] - old_center[j];
dist += t * t;
}
max_center_shift = std::max(max_center_shift, dist);
}
}
}
bool isLastIter = (++iter == MAX(criteria.maxCount, 2) || max_center_shift <= criteria.epsilon);
if (isLastIter)//是最後一次的話,就再計算下每個樣本離聚類中心的距離,不重新分配標籤以防出現空集合
{
// don't re-assign labels to avoid creation of empty clusters
parallel_for_(Range(0, N), KMeansDistanceComputer<true>(dists.data(), labels, data, centers), (double)divUp((size_t)(dims * N), CV_KMEANS_PARALLEL_GRANULARITY));
compactness = sum(Mat(Size(N, 1), CV_64F, &dists[0]))[0];// 記錄距離和
break;
}
else // 不是最後一次的話,計算距離的同時還要重新分配下標籤,可能會導致空集合
{
// assign labels
parallel_for_(Range(0, N), KMeansDistanceComputer<false>(dists.data(), labels, data, centers), (double)divUp((size_t)(dims * N * K), CV_KMEANS_PARALLEL_GRANULARITY));
}
}
//compactness將記錄所有距離,這裡的距離是指,所有的特徵向量到其聚類中心的距離之和,用於評價當前的聚類結果
if (compactness < best_compactness)
{
best_compactness = compactness;
if (_centers.needed())
{
if (_centers.fixedType() && _centers.channels() == dims)
centers.reshape(dims).copyTo(_centers);
else
centers.copyTo(_centers);
}
_labels.copyTo(best_labels);
}
}
return best_compactness;
}
2 使用超畫素的區域分割
超畫素影象分割基於依賴於影象的顏色資訊及空間關係資訊,將影象分割為遠超於目標個數、遠小於畫素數量的超畫素塊,達到儘可能保留影象中所有目標的邊緣資訊的目的,從而更好的輔助後續視覺任務(如目標檢測、目標跟蹤、語意分割等)。
超畫素是由一系列位置相鄰,顏色、亮度、紋理等特徵相似的畫素點組成的小區域,我們將其視為具有代表性的大「畫素」,稱為超畫素。超畫素技術通過畫素的組合得到少量(相對於畫素數量)具有感知意義的超畫素區域,代替大量原始畫素表達影象特徵,可以極大地降低影象處理的複雜度、減小計算量。超畫素分割的結果是覆蓋整個影象的子區域的集合,或從影象中提取的輪廓線的集合。 超畫素的數量越少,喪失的細節特徵越多,但仍然能基本保留主要區域之間的邊界及影象的基本拓撲。

常用的超畫素分割方法有:簡單線性迭代聚類(Simple Linear Iterative Clustering,SLIC)、能量驅動取樣(Super-pixels Extracted via Energy-Driven Sampling,SEEDS)和線性譜聚類(Linear Spectral Clustering,LSC)。SLIC超畫素演演算法是對上節討論的k均值演演算法的一種改進,通常使用(但不限於)包含三個顏色分量和兩個空間座標的五維向量。
OpenCV 在 ximgproc 模組提供了ximgproc.createSuperpixelSLIC函數實現SLIC演演算法。需要編譯opencv_contrib模組,可以參考VS2019編譯Opencv4.6.0GPU版本,記得勾選ximgproc。
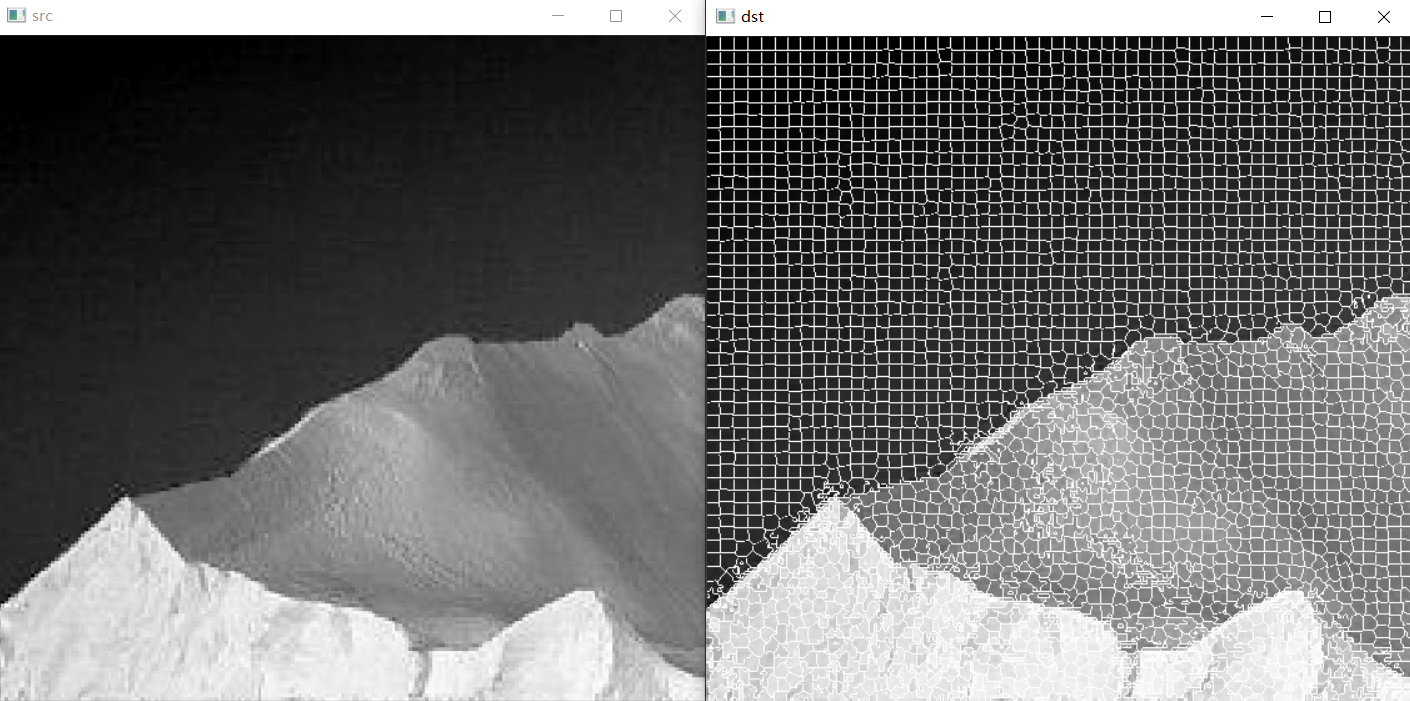
範例 SLIC超畫素區域分割
#include<opencv2/ximgproc.hpp>
using namespace ximgproc;
...
Mat src = imread("./14.tif");
Mat slicLabel, slicMask, slicColor, slicDst;
Ptr<SuperpixelLSC> slic = createSuperpixelLSC(src);
slic->iterate(10);//迭代次數
slic->getLabels(slicLabel);//獲取labels
slic->getLabelContourMask(slicMask);//獲取超畫素的邊界
int number = slic->getNumberOfSuperpixels();//獲取超畫素的數量
src.setTo(Scalar(255, 255, 255), slicMask);
參考
1. 岡薩雷斯《數位影像處理(第四版)》Chapter 10(所有圖片可在連結中下載)
2. 【youcans 的 OpenCV 例程200篇】171.SLIC 超畫素區域分割