Blog2:nchu-software-oop-2022-4+5+期中
Blog2:nchu-software-oop-2022-4+5+期中
一、前言
兩次大作業是關於四邊形和五邊形的相關操作,類似於之前的三角形,但由於圖形邊數的變化,難度大大增加。對數學知識的運用考察較多,其中還有對正規表示式的考量。在完成五邊形第二題作業是,由於前面建立的類並不好,在面對複雜的五邊形時,前面的類根本沒有辦法延用。這兩次作業對我來說都很吃力。考查的知識點有:字串的輸出和輸入,強制轉化變數的型別,split函數的應用,邏輯思維能力,全面考慮問題的能力,方法編寫能力,正規表示式練習。其中,主要題目是圖形介面類設計編寫。這些作業題量和難度都很大,全部儘量寫到最好要花費比較多的時間。
期中考試主要考察了PTA圖形介面類設計編寫,共有三道題目,題量一般。與平時題目不同的是,每題均給出了相應的類圖,要求考生按照類圖來書寫自己的程式碼。且三題呈遞進關係,每題均是由上一題進階而來。第一題是點與線,要求輸出點和線的屬性,考察了學生對Java類的設計的掌握。而第二題則是在第一題的基礎上加上了關於面的類,並要求把點、線、面三類均作為新建類Element類的子類。考察了學生對繼承與多型的掌握。第三題考察了Java容器類,主要是ArrayList的應用。且相比前兩題有了多種輸入格式,增加了難度。
二、設計與分析
題目1:
使用者輸入一組選項和資料,進行與四邊形有關的計算。
以下四邊形頂點的座標要求按順序依次輸入,連續輸入的兩個頂點是相鄰頂點,第一個和最後一個輸入的頂點相鄰。
選項包括:
1:輸入四個點座標,判斷是否是四邊形、平行四邊形,判斷結果輸出true/false,結果之間以一個英文空格符分隔。
2:輸入四個點座標,判斷是否是菱形、矩形、正方形,判斷結果輸出true/false,結果之間以一個英文空格符分隔。 若四個點座標無法構成四邊形,輸出"not a quadrilateral"
3:輸入四個點座標,判斷是凹四邊形(false)還是凸四邊形(true),輸出四邊形周長、面積,結果之間以一個英文空格符分隔。 若四個點座標無法構成四邊形,輸出"not a quadrilateral"
4:輸入六個點座標,前兩個點構成一條直線,後四個點構成一個四邊形或三角形,輸出直線與四邊形(也可能是三角形)相交的交點數量。如果交點有兩個,再按面積從小到大輸出四邊形(或三角形)被直線分割成兩部分的面積(不換行)。若直線與四邊形或三角形的一條邊線重合,輸出"The line is coincide with one of the lines"。若後四個點不符合四邊形或三角形的輸入,輸出"not a quadrilateral or triangle"。
後四個點構成三角形的情況:假設三角形一條邊上兩個端點分別是x、y,邊線中間有一點z,另一頂點s:
1)符合要求的輸入:頂點重複或者z與xy都相鄰,如x x y s、x z y s、x y x s、s x y y。此時去除冗餘點,保留一個x、一個y。
2) 不符合要求的輸入:z 不與xy都相鄰,如z x y s、x z s y、x s z y
5:輸入五個點座標,輸出第一個是否在後四個點所構成的四邊形(限定為凸四邊形,不考慮凹四邊形)或三角形(判定方法見選項4)的內部(若是四邊形輸出in the quadrilateral/outof the quadrilateral,若是三角形輸出in the triangle/outof the triangle)。如果點在多邊形的某條邊上,輸出"on the triangle或者on the quadrilateral"。若後四個點不符合四邊形或三角形,輸出"not a quadrilateral or triangle"。
*****************************************************************************************************************************************************************************
這題題目難度還好,主要根據前面三角形的類和方法,在其基礎上新增修改。
import java.util.Scanner;
class Point
{
double x;
double y;
int flag=0;
int exist=1;//1:存在 0:不存在 2:交點無數個
public boolean pointchonghe(Point A,Point B)//判斷兩點重合
{
if(A.x==B.x&&A.y==B.y)
return true;
else
return false;
}
public boolean Pointscoincide(Point A,Point B,Point C,Point D)//判斷四邊形四點重合
{
if(A.x==B.x&&A.y==B.y||A.x==C.x&&A.y==C.y||A.x==D.x&&A.y==D.y||B.x==C.x&&B.y==C.y||B.x==D.x&&B.y==D.y||C.x==D.x&&C.y==D.y)
return true;
else
return false;
}
}
class Line
{
Point p1=new Point();
Point p2=new Point();
double a;
double b;
double c;
double D;
int flag;//交點是否線上段上
public void L(Line l)//一般式係數
{
l.a=l.p2.y-l.p1.y;
l.b=l.p1.x-l.p2.x;
l.c=l.p2.x*l.p1.y-l.p1.x*l.p2.y;
}
public void D(Point p1,Point p2,Line lp1p2)//兩點間距離
{
lp1p2.D=Math.sqrt(Math.pow(lp1p2.p1.x-lp1p2.p2.x,2)+Math.pow(lp1p2.p1.y-lp1p2.p2.y,2));
lp1p2.D=Math.round(lp1p2.D*1000000000)/(double)1000000000;
}
public void distanse(Line l)//求線段距離D
{
l.D=Math.sqrt(Math.pow(l.p1.x-l.p2.x,2)+Math.pow(l.p1.y-l.p2.y,2));
l.D=Math.round(l.D*1000000000)/(double)1000000000;
}
public boolean zhixian(Point X,Line l)//點是否在直線上
{
L(l);
if(l.a*X.x+l.b*X.y+l.c==0)
return true;
else
return false;
}
public boolean linechonghe(Line l1,Line l2)//判斷是否兩線重合
{
L(l1);
L(l2);
if(l1.b==0&&l2.b==0)
{
if(l1.c/l1.a==l2.c/l2.a)
return true;
else
return false;
}
else if(l1.a==0&&l2.a==0)
{
if(l1.c/l1.b==l2.c/l2.b)
return true;
else
return false;
}
else
{
if(l1.c/l1.a==l2.c/l2.a&&l1.c/l1.b==l2.c/l2.b)
return true;
else
return false;
}
}
public boolean pingxing(Line l1,Line l2)//判斷是否平行(有無交點)
{
L(l1);
L(l2);
if(l1.b==0&&l2.b==0)
return true;
else if(l1.b!=0&&l2.b!=0&&(l1.a/l1.b==l2.a/l2.b))
return true;
else
return false;
}
public boolean Quadrilateral(Line lAB,Point C,Point D)//判斷是否四邊形
{
L(lAB);
if((!zhixian(C,lAB))&&(!zhixian(D,lAB))&&((lAB.a*C.x+lAB.b*C.y+lAB.c<0)&&(lAB.a*D.x+lAB.b*D.y+lAB.c<0)||(lAB.a*C.x+lAB.b*C.y+lAB.c>0)&&(lAB.a*D.x+lAB.b*D.y+lAB.c>0)))
return true;
else
return false;
}
public boolean Quadrilateral1(Point A,Point B,Point C,Point D,Quadrilateral Q)//凹
{
if((!zhixian(C,Q.l1))&&(!zhixian(D,Q.l1))&&(!zhixian(D,Q.l6))&&(!zhixian(D,Q.l2)))
{
Point O=new Point();
Line lAO=new Line();
lAO.p1=A;
lAO.p2=O;
Line lBO=new Line();
lBO.p1=B;
lBO.p2=O;
Line lCO=new Line();
lCO.p1=C;
lCO.p2=O;
Line lDO=new Line();
lDO.p1=D;
lDO.p2=O;
Triangle t=new Triangle();
t.jiaodian(Q.l5,Q.l6,O);//AC和BD交點
if(t.pointwhere(O,A,C,lAO,lCO,Q.l6)&&!t.pointwhere(O,B,D,lBO,lDO,Q.l5))//交點線上段AC和不在BD上
{
Q.l5.flag=0;
Q.l6.flag=1;
return true;
}
else if(!t.pointwhere(O,A,C,lAO,lCO,Q.l6)&&t.pointwhere(O,B,D,lBO,lDO,Q.l5))//交點不線上段AC和在BD上
{
Q.l5.flag=1;
Q.l6.flag=0;
return true;
}
else
return false;
}
else
return false;
}
public boolean Quadrilateral2(Point A,Point B,Point C,Point D,Quadrilateral Q)//凸
{
if((!zhixian(C,Q.l1))&&(!zhixian(D,Q.l1))&&(!zhixian(A,Q.l3))&&(!zhixian(D,Q.l2))&&(!A.Pointscoincide(A,B,C,D)))
{
Point O=new Point();
Line lAO=new Line();
lAO.p1=A;
lAO.p2=O;
Line lBO=new Line();
lBO.p1=B;
lBO.p2=O;
Line lCO=new Line();
lCO.p1=C;
lCO.p2=O;
Line lDO=new Line();
lDO.p1=D;
lDO.p2=O;
Triangle t=new Triangle();
t.jiaodian(Q.l5,Q.l6,O);//AC和BD交點
if(O.exist==1&&t.pointwhere(O,A,C,lAO,lCO,Q.l6)&&t.pointwhere(O,B,D,lBO,lDO,Q.l5))//交點線上段AC和BD上
return true;
else
return false;
}
else
return false;
}
public boolean pingxingQuadrilateral(Line l1,Line l2)//判斷是否平行四邊形
{
distanse(l1);
distanse(l2);
if(pingxing(l1,l2)&&l1.D==l2.D)
return true;
else
return false;
}
}
class Triangle
{
Line l1=new Line();
Line l2=new Line();
Line l3=new Line();
double S;
int num;
int flag=0;//1:存在,0:不存在
public boolean sanjiaox(Line l1,Line l2,Line l3)//判斷是否為三角形
{
l1.distanse(l1);
l2.distanse(l2);
l3.distanse(l3);
if((l1.D+l2.D>l3.D&&l1.D<=l3.D&&l2.D<=l3.D)||(l1.D+l3.D>l2.D&&l1.D<=l2.D&&l3.D<=l2.D)||(l2.D+l3.D>l1.D&&l2.D<=l1.D&&l2.D<=l1.D))
return true;
else
return false;
}
public void whichsanjiaox(Point C,Point D,Point E,Point F,Line lAB,Triangle tDEF,Triangle tCEF,Triangle tCDF,Triangle tCDE,Quadrilateral Q)//判斷四個點構成哪種三角形
{
if(sanjiaox(tDEF.l1,tDEF.l2,tDEF.l3)&&pointwhere(C,D,F,Q.l1,Q.l4,Q.l5))
{
if(lAB.linechonghe(lAB,Q.l1)||lAB.linechonghe(lAB,Q.l2)||lAB.linechonghe(lAB,Q.l3)||lAB.linechonghe(lAB,Q.l4))
{
System.out.print("The line is coincide with one of the lines");
return;
}
else
tDEF.flag=1;
}
else if(sanjiaox(tCEF.l1,tCEF.l2,tCEF.l3)&&pointwhere(D,C,E,Q.l1,Q.l2,Q.l6))
{
if(lAB.linechonghe(lAB,Q.l1)||lAB.linechonghe(lAB,Q.l2)||lAB.linechonghe(lAB,Q.l3)||lAB.linechonghe(lAB,Q.l4))
{
System.out.print("The line is coincide with one of the lines");
return;
}
else
tCEF.flag=1;
}
else if(sanjiaox(tCDF.l1,tCDF.l2,tCDF.l3)&&pointwhere(E,D,F,Q.l2,Q.l3,Q.l5))
{
if(lAB.linechonghe(lAB,Q.l1)||lAB.linechonghe(lAB,Q.l2)||lAB.linechonghe(lAB,Q.l3)||lAB.linechonghe(lAB,Q.l4))
{
System.out.print("The line is coincide with one of the lines");
return;
}
else
tCDF.flag=1;
}
else if(sanjiaox(tCDE.l1,tCDE.l2,tCDE.l3)&&pointwhere(F,C,E,Q.l4,Q.l3,Q.l6))
{
if(lAB.linechonghe(lAB,Q.l1)||lAB.linechonghe(lAB,Q.l2)||lAB.linechonghe(lAB,Q.l3)||lAB.linechonghe(lAB,Q.l4))
{
System.out.print("The line is coincide with one of the lines");
return;
}
else
tCDE.flag=1;
}
}
public void whichsanjiaox1(Point C,Point D,Point E,Point F,Triangle tDEF,Triangle tCEF,Triangle tCDF,Triangle tCDE,Quadrilateral Q)//判斷哪種三角形
{
if(sanjiaox(tDEF.l1,tDEF.l2,tDEF.l3)&&pointwhere(C,D,F,Q.l1,Q.l4,Q.l5))
tDEF.flag=1;
else if(sanjiaox(tCEF.l1,tCEF.l2,tCEF.l3)&&pointwhere(D,C,E,Q.l1,Q.l2,Q.l6))
tCEF.flag=1;
else if(sanjiaox(tCDF.l1,tCDF.l2,tCDF.l3)&&pointwhere(E,D,F,Q.l2,Q.l3,Q.l5))
tCDF.flag=1;
else if(sanjiaox(tCDE.l1,tCDE.l2,tCDE.l3)&&pointwhere(F,C,E,Q.l4,Q.l3,Q.l6))
tCDE.flag=1;
}
public void jiaodian(Line l1,Line l2,Point O)//兩條直線交點
{
if(l1.pingxing(l1,l2))
{
O.exist=0;
}
else
{
l1.L(l1);
l2.L(l2);
O.x=(l1.b*l2.c-l2.b*l1.c)/(l1.a*l2.b-l2.a*l1.b);
O.y=(l2.a*l1.c-l1.a*l2.c)/(l1.a*l2.b-l2.a*l1.b);
O.x=Math.round(O.x*1000000000)/(double)1000000000;
O.y=Math.round(O.y*1000000000)/(double)1000000000;
}
}
public boolean pointwhere(Point A,Point B,Point C,Line lAB,Line lAC,Line lBC)//點A是否線上段BC上
{
if(A.pointchonghe(A,B)||A.pointchonghe(A,C))
return true;
else
{
lAB.D(A,B,lAB);
lAC.D(A,C,lAC);
lBC.D(B,C,lBC);
if(lAB.D+lAC.D-lBC.D<0.000001)
return true;
else
return false;
}
}
public void jiaodiannum(Point P1,Point P2,Point P3,Line lAB,Triangle t)//交點數(線和三角形)
{
t.num=0;
P1.flag=0;
P2.flag=0;
P3.flag=0;
t.jiaodian(lAB,t.l1,P1);
Line lp11=new Line();
lp11.p1=P1;
lp11.p2=t.l1.p1;
Line lp12=new Line();
lp12.p1=P1;
lp12.p2=t.l1.p2;
if(P1.exist==1&&t.pointwhere(P1, t.l1.p1, t.l1.p2,lp11,lp12,t.l1))
{
t.num++;
P1.flag=1;//交點線上段上
}
t.jiaodian(lAB,t.l2,P2);
Line lp21=new Line();
lp21.p1=P2;
lp21.p2=t.l2.p1;
Line lp22=new Line();
lp22.p1=P2;
lp22.p2=t.l2.p2;
if(P2.exist==1&&t.pointwhere(P2,t.l2.p1,t.l2.p2,lp21,lp22,t.l2))
{
if(P1.flag==0||(!P1.pointchonghe(P1,P2)&&P1.flag==1))
{
t.num++;
P2.flag=1;
}
}
t.jiaodian(lAB,t.l3,P3);
Line lp31=new Line();
lp31.p1=P3;
lp31.p2=t.l3.p1;
Line lp32=new Line();
lp32.p1=P3;
lp32.p2=t.l3.p2;
if(P3.exist==1&&t.pointwhere(P3,t.l3.p1,t.l3.p2,lp31,lp32,t.l3))
{
if(P1.flag==0&&P2.flag==0)
{
t.num++;
P3.flag=1;
}
else if(P1.flag==1&&P2.flag==0&&!P1.pointchonghe(P1,P3))
{
t.num++;
P3.flag=1;
}
else if(P1.flag==0&&P2.flag==1&&!P2.pointchonghe(P2,P3))
{
t.num++;
P3.flag=1;
}
}
}
public void sanjiaoxmianji(Triangle t)//三角形面積
{
t.l1.distanse(t.l1);
t.l2.distanse(t.l2);
t.l3.distanse(t.l3);
double x=(t.l1.D+t.l2.D+t.l3.D)/2;
t.S=Math.sqrt(x*(x-t.l1.D)*(x-t.l2.D)*(x-t.l3.D));
}
public void xiaomianji(Point P1,Point P2,Point P3,Triangle t,Triangle T)//切割小三角形面積
{
if(P1.flag==1&&P2.flag==1)//三角形CP1P2
{
t.l1.p1=T.l1.p2;
t.l1.p2=P1;
t.l2.p1=T.l1.p2;
t.l2.p2=P2;
t.l3.p1=P1;
t.l3.p2=P2;
t.sanjiaoxmianji(t);
}
else if(P1.flag==1&&P3.flag==1)
{
t.l1.p1=T.l1.p1;
t.l1.p2=P1;
t.l2.p1=T.l1.p1;
t.l2.p2=P3;
t.l3.p1=P1;
t.l3.p2=P3;
t.sanjiaoxmianji(t);
}
else if(P2.flag==1&&P3.flag==1)
{
t.l1.p1=T.l2.p2;
t.l1.p2=P2;
t.l2.p1=T.l2.p2;
t.l2.p2=P3;
t.l3.p1=P2;
t.l3.p2=P3;
t.sanjiaoxmianji(t);
}
}
public void xiaomianji1(Point P1,Point P2,Point P3,Point P4,Triangle t,Quadrilateral Q)//四邊形切割小三角形面積
{
if(P1.flag==1&&P2.flag==1)//三角形DP1P2
{
t.l1.p1=Q.l1.p2;
t.l1.p2=P1;
t.l2.p1=Q.l1.p2;
t.l2.p2=P2;
t.l3.p1=P1;
t.l3.p2=P2;
t.sanjiaoxmianji(t);
}
else if(P1.flag==1&&P4.flag==1)//CP1P4
{
t.l1.p1=Q.l1.p1;
t.l1.p2=P1;
t.l2.p1=Q.l1.p1;
t.l2.p2=P4;
t.l3.p1=P1;
t.l3.p2=P4;
t.sanjiaoxmianji(t);
}
else if(P2.flag==1&&P3.flag==1)//EP2P3
{
t.l1.p1=Q.l2.p2;
t.l1.p2=P2;
t.l2.p1=Q.l2.p2;
t.l2.p2=P3;
t.l3.p1=P2;
t.l3.p2=P3;
t.sanjiaoxmianji(t);
}
else if(P3.flag==1&&P4.flag==1)//FP3P4
{
t.l1.p1=Q.l3.p2;
t.l1.p2=P3;
t.l2.p1=Q.l3.p2;
t.l2.p2=P4;
t.l3.p1=P3;
t.l3.p2=P4;
t.sanjiaoxmianji(t);
}
}
}
class Quadrilateral
{
Line l1=new Line();
Line l2=new Line();
Line l3=new Line();
Line l4=new Line();
Line l5=new Line();//BD
Line l6=new Line();//AC
double C;
double S;
int num;
int flag;//1:存在 0:不存在
int aotu;//1:凸 0:凹
public boolean lingxing(Quadrilateral Q)//菱形
{
if(!Q.l1.pingxingQuadrilateral(Q.l1,Q.l3))
return false;
else
{
Q.l1.distanse(Q.l1);
Q.l2.distanse(Q.l2);
if(Q.l1.D==Q.l2.D)
return true;
else
return false;
}
}
public boolean zhijiao(Quadrilateral Q)//判斷直角
{
Q.l1.distanse(Q.l1);
Q.l4.distanse(Q.l4);
Q.l5.distanse(Q.l5);
if(Q.l1.D*Q.l1.D+Q.l4.D*Q.l4.D-Q.l5.D*Q.l5.D<0.000000000001)
return true;
else
return false;
}
public boolean juxing(Quadrilateral Q)//矩形
{
if(!Q.l1.pingxingQuadrilateral(Q.l1,Q.l3))
return false;
else
{
if(zhijiao(Q))
return true;
else
return false;
}
}
public boolean zhengfangxing(Quadrilateral Q)//正方形
{
if(!Q.juxing(Q))
return false;
else
{
Q.l1.distanse(Q.l1);
Q.l2.distanse(Q.l2);
if(Q.l1.D==Q.l2.D)
return true;
else
return false;
}
}
public void Quadrilateralzhouchang(Quadrilateral Q)//四邊形周長
{
Q.l1.distanse(Q.l1);
Q.l2.distanse(Q.l2);
Q.l3.distanse(Q.l3);
Q.l4.distanse(Q.l4);
Q.C=Q.l1.D+Q.l2.D+Q.l3.D+Q.l4.D;
}
public void Quadrilateralmianji(Quadrilateral Q)//凸四邊形面積
{
Q.l1.distanse(Q.l1);
Q.l2.distanse(Q.l2);
Q.l3.distanse(Q.l3);
Q.l4.distanse(Q.l4);
Q.l5.distanse(Q.l5);
double x1=(l1.D+l4.D+l5.D)/2;
double s1=Math.sqrt(x1*(x1-l1.D)*(x1-l4.D)*(x1-l5.D));
double x2=(l2.D+l3.D+l5.D)/2;
double s2=Math.sqrt(x2*(x2-l2.D)*(x2-l3.D)*(x2-l5.D));
Q.S=s1+s2;
}
public void Quadrilateralmianji1(Quadrilateral Q)//凹四邊形面積
{
if(Q.l5.flag==0&&Q.l6.flag==1)
{
Quadrilateralmianji(Q);
}
else if(Q.l5.flag==1&&Q.l6.flag==0)
{
Q.l1.distanse(Q.l1);
Q.l2.distanse(Q.l2);
Q.l3.distanse(Q.l3);
Q.l4.distanse(Q.l4);
Q.l6.distanse(Q.l6);
double x1=(l1.D+l2.D+l6.D)/2;
double s1=Math.sqrt(x1*(x1-l1.D)*(x1-l2.D)*(x1-l6.D));
double x2=(l3.D+l4.D+l6.D)/2;
double s2=Math.sqrt(x2*(x2-l3.D)*(x2-l4.D)*(x2-l6.D));
Q.S=s1+s2;
}
}
public void Quadrilateralnum(Point P1,Point P2,Point P3,Point P4,Line lAB,Triangle T,Quadrilateral Q)//交點數(線和四邊形)
{
Q.num=0;
P1.flag=0;
P2.flag=0;
P3.flag=0;
P4.flag=0;
T.jiaodian(lAB,Q.l1,P1);
Line lp11=new Line();
lp11.p1=P1;
lp11.p2=Q.l1.p1;
Line lp12=new Line();
lp12.p1=P1;
lp12.p2=Q.l1.p2;
if(P1.exist==1&&T.pointwhere(P1,Q.l1.p1,Q.l1.p2,lp11,lp12,Q.l1))
{
Q.num++;
P1.flag=1;//交點線上段上
}
T.jiaodian(lAB,Q.l2,P2);
Line lp21=new Line();
lp21.p1=P2;
lp21.p2=Q.l2.p1;
Line lp22=new Line();
lp22.p1=P2;
lp22.p2=Q.l2.p2;
if(P2.exist==1&&T.pointwhere(P2,Q.l2.p1,Q.l2.p2,lp21,lp22,Q.l2))
{
if(P1.flag==0||(!P1.pointchonghe(P1,P2)&&P1.flag==1))
{
Q.num++;
P2.flag=1;
}
}
T.jiaodian(lAB,Q.l3,P3);
Line lp31=new Line();
lp31.p1=P3;
lp31.p2=Q.l3.p1;
Line lp32=new Line();
lp32.p1=P3;
lp32.p2=Q.l3.p2;
if(P3.exist==1&&T.pointwhere(P3,Q.l3.p1,Q.l3.p2,lp31,lp32,Q.l3))
{
if(P1.flag==0&&P2.flag==0)
{
Q.num++;
P3.flag=1;
}
else if(P1.flag==1&&P2.flag==0&&!P1.pointchonghe(P1,P3))
{
Q.num++;
P3.flag=1;
}
else if(P1.flag==0&&P2.flag==1&&!P2.pointchonghe(P2,P3))
{
Q.num++;
P3.flag=1;
}
}
T.jiaodian(lAB,Q.l4,P4);
Line lp41=new Line();
lp41.p1=P4;
lp41.p2=Q.l4.p1;
Line lp42=new Line();
lp42.p1=P4;
lp42.p2=Q.l4.p2;
if(P4.exist==1&&T.pointwhere(P4,Q.l4.p1,Q.l4.p2,lp41,lp42,Q.l4))
{
if(P1.flag==0&&P2.flag==0&&P3.flag==0)
{
Q.num++;
P4.flag=1;
}
else if(P1.flag==1&&P2.flag==0&&P3.flag==0&&!P1.pointchonghe(P1,P4))
{
Q.num++;
P4.flag=1;
}
else if(P1.flag==0&&P2.flag==1&&P3.flag==0&&!P2.pointchonghe(P2,P4))
{
Q.num++;
P4.flag=1;
}
else if(P1.flag==0&&P2.flag==0&&P3.flag==1&&!P3.pointchonghe(P3,P4))
{
Q.num++;
P4.flag=1;
}
}
}
}
public class Main
{
public static void main(String[] args)
{
Scanner in=new Scanner(System.in);
String a=in.nextLine();
int num=(int)a.charAt(0)-(int)'0';
String[] tokens=a.split(" ");
int length=tokens.length;
for(int i=0;i<length;i++)
{
if(i==0)
{
if(!tokens[i].matches("^\\d:[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?),[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$"))
{
System.out.print("Wrong Format");
return;
}
}
else if(i!=0)
{
if(!tokens[i].matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?),[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$"))
{
System.out.print("Wrong Format");
return;
}
}
}
if(((num==1||num==2||num==3)&&length!=4)||(num==4&&length!=6)||(num==5&&length!=5))
{
System.out.print("wrong number of points");
return;
}
String[] arr=a.split(" |:|,");
switch(num)
{
case 1:
{
Line lAB=new Line();
Point C=new Point();
Point D=new Point();
lAB.p1.x=Double.valueOf(arr[1]);
lAB.p1.y=Double.valueOf(arr[2]);
lAB.p2.x=Double.valueOf(arr[3]);
lAB.p2.y=Double.valueOf(arr[4]);
C.x=Double.valueOf(arr[5]);
C.y=Double.valueOf(arr[6]);
D.x=Double.valueOf(arr[7]);
D.y=Double.valueOf(arr[8]);
Line lCD=new Line();
lCD.p1=C;
lCD.p2=D;
Line lBC=new Line();
lBC.p1=lAB.p2;
lBC.p2=C;
if(lAB.p1.Pointscoincide(lAB.p1,lAB.p2,C,D))
{
System.out.print("points coincide");return;
}
if(lAB.Quadrilateral(lAB,C,D)&&lBC.Quadrilateral(lBC,lAB.p1,D))
{
System.out.print("true");
if(lAB.pingxingQuadrilateral(lAB,lCD))
System.out.print(" true");
else
System.out.print(" false");
}
else
System.out.print("false false");
break;
}
case 2:
{
Quadrilateral Q=new Quadrilateral();
Q.l1.p1.x=Double.valueOf(arr[1]);
Q.l1.p1.y=Double.valueOf(arr[2]);
Q.l1.p2.x=Double.valueOf(arr[3]);
Q.l1.p2.y=Double.valueOf(arr[4]);
Q.l2.p1=Q.l1.p2;
Q.l2.p2.x=Double.valueOf(arr[5]);
Q.l2.p2.y=Double.valueOf(arr[6]);
Q.l3.p1=Q.l2.p2;
Q.l3.p2.x=Double.valueOf(arr[7]);
Q.l3.p2.y=Double.valueOf(arr[8]);
Q.l4.p1=Q.l1.p1;
Q.l4.p2=Q.l3.p2;
Q.l5.p1=Q.l1.p2;
Q.l5.p2=Q.l4.p2;
if(Q.l1.p1.Pointscoincide(Q.l1.p1,Q.l1.p2,Q.l3.p1,Q.l3.p2))
{
System.out.print("not a quadrilateral");return;
}
if(!Q.l1.Quadrilateral(Q.l1,Q.l3.p1,Q.l3.p2)||!Q.l2.Quadrilateral(Q.l2,Q.l4.p1,Q.l4.p2))
{
System.out.print("not a quadrilateral");return;
}
if(Q.lingxing(Q))
System.out.print("true");
else
System.out.print("false");
if(Q.juxing(Q))
System.out.print(" true");
else
System.out.print(" false");
if(Q.zhengfangxing(Q))
System.out.print(" true");
else
System.out.print(" false");
break;
}
case 3:
{
Quadrilateral Q=new Quadrilateral();
Q.l1.p1.x=Double.valueOf(arr[1]);
Q.l1.p1.y=Double.valueOf(arr[2]);
Q.l1.p2.x=Double.valueOf(arr[3]);
Q.l1.p2.y=Double.valueOf(arr[4]);
Q.l2.p1=Q.l1.p2;
Q.l2.p2.x=Double.valueOf(arr[5]);
Q.l2.p2.y=Double.valueOf(arr[6]);
Q.l3.p1=Q.l2.p2;
Q.l3.p2.x=Double.valueOf(arr[7]);
Q.l3.p2.y=Double.valueOf(arr[8]);
Q.l4.p1=Q.l1.p1;
Q.l4.p2=Q.l3.p2;
Q.l5.p1=Q.l1.p2;
Q.l5.p2=Q.l4.p2;
Q.l6.p1=Q.l1.p1;
Q.l6.p2=Q.l2.p2;
Point A=new Point();
Point B=new Point();
Point C=new Point();
Point D=new Point();
A.x=Double.valueOf(arr[1]);
A.y=Double.valueOf(arr[2]);
B.x=Double.valueOf(arr[3]);
B.y=Double.valueOf(arr[4]);
C.x=Double.valueOf(arr[5]);
C.y=Double.valueOf(arr[6]);
D.x=Double.valueOf(arr[7]);
D.y=Double.valueOf(arr[8]);
if(Q.l1.p1.Pointscoincide(Q.l1.p1,Q.l1.p2,Q.l3.p1,Q.l3.p2))
{
System.out.print("not a quadrilateral");return;
}
int X;
if(Q.l1.Quadrilateral(Q.l1,Q.l3.p1,Q.l3.p2)&&Q.l2.Quadrilateral(Q.l2,Q.l4.p1,Q.l4.p2)&&!Q.l6.zhixian(D,Q.l6)&&!Q.l6.zhixian(B,Q.l6))//涵蓋凸四邊形和D點凹進去的四邊形
{
Point o=new Point();
Line lBo=new Line();
lBo.p1=B;
lBo.p2=o;
Line lDo=new Line();
lDo.p1=D;
lDo.p2=o;
Line lAo=new Line();
lAo.p1=A;
lAo.p2=o;
Line lCo=new Line();
lCo.p1=C;
lCo.p2=o;
Triangle t=new Triangle();
t.jiaodian(Q.l5,Q.l6,o);
if(!t.pointwhere(o,Q.l5.p1,Q.l5.p2,lBo,lDo,Q.l5)&&t.pointwhere(o,Q.l6.p1,Q.l6.p2,lAo,lCo,Q.l6))
{
X=0;
Q.l5.flag=0;
Q.l6.flag=1;
System.out.print("false ");
}
else
{
X=1;
System.out.print("true ");
}
}
else
{
if(Q.l5.Quadrilateral1(A,B,C,D,Q))//凹四邊形
{
X=0;
System.out.print("false ");
}
else
{
System.out.print("not a quadrilateral");
return;
}
}
Q.Quadrilateralzhouchang(Q);//周長面積
System.out.print(Math.round(Q.C*1000)/(double)1000);
if(X==1)
{
System.out.print(" ");
Q.Quadrilateralmianji(Q);
System.out.print(Math.round(Q.S*1000)/(double)1000);
}
else if(X==0)
{
System.out.print(" ");
Q.Quadrilateralmianji1(Q);
System.out.print(Math.round(Q.S*1000)/(double)1000);
}
break;
}
case 4:
{
Point A=new Point();
Point B=new Point();
A.x=Double.valueOf(arr[1]);
A.y=Double.valueOf(arr[2]);
B.x=Double.valueOf(arr[3]);
B.y=Double.valueOf(arr[4]);
Line lAB=new Line();
lAB.p1=A;
lAB.p2=B;
if(A.pointchonghe(A,B))
{
System.out.print("points coincide");return;
}
Point C=new Point();
Point D=new Point();
Point E=new Point();
Point F=new Point();
C.x=Double.valueOf(arr[5]);
C.y=Double.valueOf(arr[6]);
D.x=Double.valueOf(arr[7]);
D.y=Double.valueOf(arr[8]);
E.x=Double.valueOf(arr[9]);
E.y=Double.valueOf(arr[10]);
F.x=Double.valueOf(arr[11]);
F.y=Double.valueOf(arr[12]);
Quadrilateral Q=new Quadrilateral();
Q.l1.p1=C;
Q.l1.p2=D;
Q.l2.p1=D;
Q.l2.p2=E;
Q.l3.p1=E;
Q.l3.p2=F;
Q.l4.p1=C;
Q.l4.p2=F;
Q.l5.p1=D;
Q.l5.p2=F;
Q.l6.p1=C;
Q.l6.p2=E;
Triangle tDEF=new Triangle();
tDEF.l1.p1=D;
tDEF.l1.p2=E;
tDEF.l2.p1=E;
tDEF.l2.p2=F;
tDEF.l3.p1=D;
tDEF.l3.p2=F;
Triangle tCEF=new Triangle();
tCEF.l1.p1=C;
tCEF.l1.p2=E;
tCEF.l2.p1=E;
tCEF.l2.p2=F;
tCEF.l3.p1=C;
tCEF.l3.p2=F;
Triangle tCDF=new Triangle();
tCDF.l1.p1=C;
tCDF.l1.p2=D;
tCDF.l2.p1=D;
tCDF.l2.p2=F;
tCDF.l3.p1=C;
tCDF.l3.p2=F;
Triangle tCDE=new Triangle();
tCDE.l1.p1=C;
tCDE.l1.p2=D;
tCDE.l2.p1=D;
tCDE.l2.p2=E;
tCDE.l3.p1=C;
tCDE.l3.p2=E;
Point P1=new Point();
Point P2=new Point();
Point P3=new Point();
Point P4=new Point();
tDEF.whichsanjiaox(C,D,E,F,lAB,tDEF,tCEF,tCDF,tCDE,Q);//判斷是哪三個點構成三角形
if(tDEF.flag==1||C.pointchonghe(C,E))//求直線AB與三角形交點數
{
if(C.pointchonghe(C,E)&&lAB.linechonghe(lAB,Q.l5))
{
System.out.print("The line is coincide with one of the lines");return;
}
tDEF.jiaodiannum(P1,P2,P3,lAB,tDEF);
System.out.print(tDEF.num);
if(tDEF.num==2)
{
System.out.print(" ");
tDEF.sanjiaoxmianji(tDEF);
Triangle t=new Triangle();
tDEF.xiaomianji(P1,P2,P3,t,tDEF);//切割小三角形面積
double s=tDEF.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
}
else if(tCEF.flag==1||D.pointchonghe(D,F))
{
if(D.pointchonghe(D,F)&&lAB.linechonghe(lAB,Q.l6))
{
System.out.print("The line is coincide with one of the lines");return;
}
tCEF.jiaodiannum(P1,P2,P3,lAB,tCEF);
System.out.print(tCEF.num);
if(tCEF.num==2)
{
System.out.print(" ");
tCEF.sanjiaoxmianji(tCEF);
Triangle t=new Triangle();
tCEF.xiaomianji(P1,P2,P3,t,tCEF);//切割小三角形面積
double s=tCEF.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
}
else if(tCDF.flag==1||E.pointchonghe(E,C))
{
if(C.pointchonghe(C,E)&&lAB.linechonghe(lAB,Q.l5))
{
System.out.print("The line is coincide with one of the lines");return;
}
tCDF.jiaodiannum(P1,P2,P3,lAB,tCDF);
System.out.print(tCDF.num);
if(tCDF.num==2)
{
System.out.print(" ");
tCDF.sanjiaoxmianji(tCDF);
Triangle t=new Triangle();
tCDF.xiaomianji(P1,P2,P3,t,tCDF);//切割小三角形面積
double s=tCDF.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
}
else if(tCDE.flag==1||F.pointchonghe(F,D))
{
if(D.pointchonghe(D,F)&&lAB.linechonghe(lAB,Q.l6))
{
System.out.print("The line is coincide with one of the lines");return;
}
tCDE.jiaodiannum(P1,P2,P3,lAB,tCDE);
System.out.print(tCDE.num);
if(tCDE.num==2)
{
System.out.print(" ");
tCDE.sanjiaoxmianji(tCDE);
Triangle t=new Triangle();
tCDE.xiaomianji(P1,P2,P3,t,tCDE);//切割小三角形面積
double s=tCDE.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
}
else if(Q.l1.Quadrilateral2(C,D,E,F,Q))
{
if(lAB.linechonghe(lAB,Q.l1)||lAB.linechonghe(lAB,Q.l2)||lAB.linechonghe(lAB,Q.l3)||lAB.linechonghe(lAB,Q.l4))
{
System.out.print("The line is coincide with one of the lines");return;
}
Triangle t=new Triangle();
Q.Quadrilateralnum(P1,P2,P3,P4,lAB,t,Q);
System.out.print(Q.num);
if(Q.num==2)
{
System.out.print(" ");
Q.Quadrilateralmianji(Q);//大四邊形面積
if(P1.flag==1&&P2.flag==1)
{
t.xiaomianji1(P1,P2,P3,P4,t,Q);
double s=Q.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P1.flag==1&&P3.flag==1)
{
Triangle tCFP3=new Triangle();
tCFP3.l1.p1=C;
tCFP3.l1.p2=F;
tCFP3.l2.p1=C;
tCFP3.l2.p2=P3;
tCFP3.l3.p1=F;
tCFP3.l3.p2=P3;
tCFP3.sanjiaoxmianji(tCFP3);
Triangle tCP1P3=new Triangle();
tCP1P3.l1.p1=C;
tCP1P3.l1.p2=P1;
tCP1P3.l2.p1=C;
tCP1P3.l2.p2=P3;
tCP1P3.l3.p1=P1;
tCP1P3.l3.p2=P3;
tCP1P3.sanjiaoxmianji(tCP1P3);
double s1=tCFP3.S+tCP1P3.S;
Triangle tDP1P3=new Triangle();
tDP1P3.l1.p1=D;
tDP1P3.l1.p2=P1;
tDP1P3.l2.p1=D;
tDP1P3.l2.p2=P3;
tDP1P3.l3.p1=P1;
tDP1P3.l3.p2=P3;
tDP1P3.sanjiaoxmianji(tDP1P3);
Triangle tDEP3=new Triangle();
tDEP3.l1.p1=D;
tDEP3.l1.p2=E;
tDEP3.l2.p1=D;
tDEP3.l2.p2=P3;
tDEP3.l3.p1=E;
tDEP3.l3.p2=P3;
tDEP3.sanjiaoxmianji(tDEP3);
double s2=tDEP3.S+tDP1P3.S;
if(s1<s2)
System.out.print(Math.round(s1*1000)/(double)1000+" "+Math.round(s2*1000)/(double)1000);
else
System.out.print(Math.round(s2*1000)/(double)1000+" "+Math.round(s1*1000)/(double)1000);
}
else if(P1.flag==1&&P4.flag==1)
{
t.xiaomianji1(P1,P2,P3,P4,t,Q);
double s=Q.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P2.flag==1&&P3.flag==1)
{
t.xiaomianji1(P1,P2,P3,P4,t,Q);
double s=Q.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P2.flag==1&&P4.flag==1)
{
Triangle tCDP2=new Triangle();
tCDP2.l1.p1=C;
tCDP2.l1.p2=D;
tCDP2.l2.p1=C;
tCDP2.l2.p2=P2;
tCDP2.l3.p1=D;
tCDP2.l3.p2=P2;
tCDP2.sanjiaoxmianji(tCDP2);
Triangle tCP2P4=new Triangle();
tCP2P4.l1.p1=C;
tCP2P4.l1.p2=P2;
tCP2P4.l2.p1=C;
tCP2P4.l2.p2=P4;
tCP2P4.l3.p1=P2;
tCP2P4.l3.p2=P4;
tCP2P4.sanjiaoxmianji(tCP2P4);
double s1=tCDP2.S+tCP2P4.S;
Triangle tFP2P4=new Triangle();
tFP2P4.l1.p1=F;
tFP2P4.l1.p2=P2;
tFP2P4.l2.p1=F;
tFP2P4.l2.p2=P4;
tFP2P4.l3.p1=P2;
tFP2P4.l3.p2=P4;
tFP2P4.sanjiaoxmianji(tFP2P4);
Triangle tEFP2=new Triangle();
tEFP2.l1.p1=E;
tEFP2.l1.p2=F;
tEFP2.l2.p1=E;
tEFP2.l2.p2=P2;
tEFP2.l3.p1=F;
tEFP2.l3.p2=P2;
tEFP2.sanjiaoxmianji(tEFP2);
double s2=tFP2P4.S+tEFP2.S;
if(s1<s2)
System.out.print(Math.round(s1*1000)/(double)1000+" "+Math.round(s2*1000)/(double)1000);
else
System.out.print(Math.round(s2*1000)/(double)1000+" "+Math.round(s1*1000)/(double)1000);
}
else if(P3.flag==1&&P4.flag==1)
{
t.xiaomianji1(P1,P2,P3,P4,t,Q);
double s=Q.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
}
}
else//判斷非三角形四邊形情況
{
System.out.print("not a quadrilateral or triangle");
}
break;
}
case 5:
{
Point A=new Point();
Point C=new Point();
Point D=new Point();
Point E=new Point();
Point F=new Point();
A.x=Double.valueOf(arr[1]);
A.y=Double.valueOf(arr[2]);
C.x=Double.valueOf(arr[3]);
C.y=Double.valueOf(arr[4]);
D.x=Double.valueOf(arr[5]);
D.y=Double.valueOf(arr[6]);
E.x=Double.valueOf(arr[7]);
E.y=Double.valueOf(arr[8]);
F.x=Double.valueOf(arr[9]);
F.y=Double.valueOf(arr[10]);
Quadrilateral Q=new Quadrilateral();
Q.l1.p1=C;
Q.l1.p2=D;
Q.l2.p1=D;
Q.l2.p2=E;
Q.l3.p1=E;
Q.l3.p2=F;
Q.l4.p1=C;
Q.l4.p2=F;
Q.l5.p1=D;
Q.l5.p2=F;
Q.l6.p1=C;
Q.l6.p2=E;
Triangle tDEF=new Triangle();
tDEF.l1.p1=D;
tDEF.l1.p2=E;
tDEF.l2.p1=E;
tDEF.l2.p2=F;
tDEF.l3.p1=D;
tDEF.l3.p2=F;
Triangle tCEF=new Triangle();
tCEF.l1.p1=C;
tCEF.l1.p2=E;
tCEF.l2.p1=E;
tCEF.l2.p2=F;
tCEF.l3.p1=C;
tCEF.l3.p2=F;
Triangle tCDF=new Triangle();
tCDF.l1.p1=C;
tCDF.l1.p2=D;
tCDF.l2.p1=D;
tCDF.l2.p2=F;
tCDF.l3.p1=C;
tCDF.l3.p2=F;
Triangle tCDE=new Triangle();
tCDE.l1.p1=C;
tCDE.l1.p2=D;
tCDE.l2.p1=D;
tCDE.l2.p2=E;
tCDE.l3.p1=C;
tCDE.l3.p2=E;
Point P1=new Point();
Point P2=new Point();
Point P3=new Point();
Point P4=new Point();
Line lAC=new Line();
lAC.p1=A;
lAC.p2=C;
Line lAD=new Line();
lAD.p1=A;
lAD.p2=D;
Line lAE=new Line();
lAE.p1=A;
lAE.p2=E;
Line lAF=new Line();
lAF.p1=A;
lAF.p2=F;
int num1=0,num2=0,num3=0,num4=0;
tDEF.whichsanjiaox1(C,D,E,F,tDEF,tCEF,tCDF,tCDE,Q);//判斷是哪三個點構成三角形
if(tDEF.flag==1||C.pointchonghe(C,E))//求直線與三角形交點數
{
if(tDEF.pointwhere(A,D,E,lAD,lAE,Q.l2)||tDEF.pointwhere(A,E,F,lAE,lAF,Q.l3)||tDEF.pointwhere(A,D,F,lAD,lAF,Q.l5))
{
System.out.print("on the triangle");return;
}
tDEF.jiaodiannum(P1,P2,P3,lAD,tDEF);
num1=tDEF.num;
tDEF.jiaodiannum(P1,P2,P3,lAE,tDEF);
num2=tDEF.num;
tDEF.jiaodiannum(P1,P2,P3,lAF,tDEF);
num3=tDEF.num;
if(num1==2&&num2==2&&num3==2)
System.out.print("in the triangle");
else
System.out.print("outof the triangle");
}
else if(tCEF.flag==1||D.pointchonghe(D,F))
{
if(tCEF.pointwhere(A,C,E,lAC,lAE,Q.l6)||tCEF.pointwhere(A,E,F,lAE,lAF,Q.l3)||tCEF.pointwhere(A,C,F,lAC,lAF,Q.l4))
{
System.out.print("on the triangle");return;
}
tCEF.jiaodiannum(P1,P2,P3,lAC,tCEF);
num1=tCEF.num;
tCEF.jiaodiannum(P1,P2,P3,lAE,tCEF);
num2=tCEF.num;
tCEF.jiaodiannum(P1,P2,P3,lAF,tCEF);
num3=tCEF.num;
if(num1==2&&num2==2&&num3==2)
System.out.print("in the triangle");
else
System.out.print("outof the triangle");
}
else if(tCDF.flag==1||E.pointchonghe(E,C))
{
if(tCDF.pointwhere(A,C,D,lAC,lAD,Q.l1)||tCDF.pointwhere(A,D,F,lAD,lAF,Q.l5)||tCDF.pointwhere(A,C,F,lAC,lAF,Q.l4))
{
System.out.print("on the triangle");return;
}
tCDF.jiaodiannum(P1,P2,P3,lAC,tCDF);
num1=tCDF.num;
tCDF.jiaodiannum(P1,P2,P3,lAD,tCDF);
num2=tCDF.num;
tCDF.jiaodiannum(P1,P2,P3,lAF,tCDF);
num3=tCDF.num;
if(num1==2&&num2==2&&num3==2)
System.out.print("in the triangle");
else
System.out.print("outof the triangle");
}
else if(tCDE.flag==1||F.pointchonghe(F,D))
{
if(tCDE.pointwhere(A,C,D,lAC,lAD,Q.l1)|tCDE.pointwhere(A,D,E,lAD,lAE,Q.l2)||tCDE.pointwhere(A,C,E,lAC,lAE,Q.l6))
{
System.out.print("on the triangle");return;
}
tCDE.jiaodiannum(P1,P2,P3,lAC,tCDE);
num1=tCDE.num;
tCDE.jiaodiannum(P1,P2,P3,lAD,tCDE);
num2=tCDE.num;
tCDE.jiaodiannum(P1,P2,P3,lAE,tCDE);
num3=tCDE.num;
if(num1==2&&num2==2&&num3==2)
System.out.print("in the triangle");
else
System.out.print("outof the triangle");
}
else if(Q.l1.Quadrilateral2(C,D,E,F,Q))
{
Triangle t=new Triangle();
if(t.pointwhere(A,C,D,lAC,lAD,Q.l1)||t.pointwhere(A,D,E,lAD,lAE,Q.l2)||t.pointwhere(A,E,F,lAE,lAF,Q.l3)||t.pointwhere(A,C,F,lAC,lAF,Q.l4))
{
System.out.print("on the quadrilateral");return;
}
Triangle tACD=new Triangle();
tACD.l1.p1=A;
tACD.l1.p2=C;
tACD.l2.p1=A;
tACD.l2.p2=D;
tACD.l3.p1=C;
tACD.l3.p2=D;
Triangle tADE=new Triangle();
tADE.l1.p1=A;
tADE.l1.p2=D;
tADE.l2.p1=A;
tADE.l2.p2=E;
tADE.l3.p1=D;
tADE.l3.p2=E;
Triangle tAEF=new Triangle();
tAEF.l1.p1=A;
tAEF.l1.p2=E;
tAEF.l2.p1=A;
tAEF.l2.p2=F;
tAEF.l3.p1=E;
tAEF.l3.p2=F;
Triangle tACF=new Triangle();
tACF.l1.p1=A;
tACF.l1.p2=C;
tACF.l2.p1=A;
tACF.l2.p2=F;
tACF.l3.p1=C;
tACF.l3.p2=F;
Q.Quadrilateralmianji(Q);//四邊形面積
tACD.sanjiaoxmianji(tACD);
tADE.sanjiaoxmianji(tADE);
tAEF.sanjiaoxmianji(tAEF);
tACF.sanjiaoxmianji(tACF);
double S;
S=tACD.S+tADE.S+tAEF.S+tACF.S;
if(S-Q.S<0.001)
System.out.print("in the quadrilateral");
else
System.out.print("outof the quadrilateral");
}
else
System.out.print("not a quadrilateral or triangle");
/*
Q.Quadrilateralnum(P1,P2,P3,P4,lAC,t,Q);
num1=Q.num;
Q.Quadrilateralnum(P1,P2,P3,P4,lAD,t,Q);
num2=Q.num;
Q.Quadrilateralnum(P1,P2,P3,P4,lAE,t,Q);
num3=Q.num;
Q.Quadrilateralnum(P1,P2,P3,P4,lAF,t,Q);
num4=Q.num;
System.out.println(num1+" "+num2+" "+num3+" "+num4);
if(num1==2&&num2==2&&num3==2&&num4==2)
System.out.print("in the quadrilateral");
else
System.out.print("outof the quadrilateral");
}
else
System.out.print("not a quadrilateral or triangle");
*/
break;
}
}
}
}
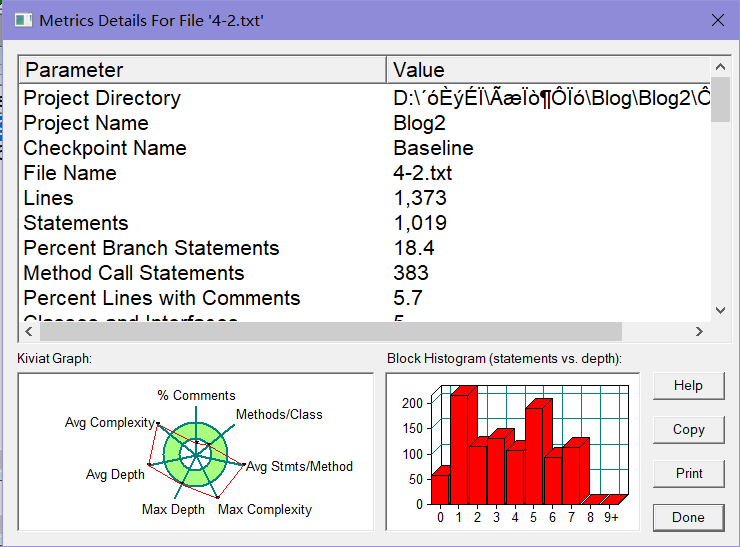
雖然使用了物件導向的方法,但是建立類是並沒有建立的很完善。
另外,很多內容還是擠在一起,沒有去單獨構造成函數。
*******************************************************************************************************************************************************
題目2:
使用者輸入一組選項和資料,進行與五邊形有關的計算。
以下五邊形頂點的座標要求按順序依次輸入,連續輸入的兩個頂點是相鄰頂點,第一個和最後一個輸入的頂點相鄰。
選項包括:
1:輸入五個點座標,判斷是否是五邊形,判斷結果輸出true/false。
2:輸入五個點座標,判斷是凹五邊形(false)還是凸五邊形(true),如果是凸五邊形,則再輸出五邊形周長、面積,結果之間以一個英文空格符分隔。 若五個點座標無法構成五邊形,輸出"not a pentagon"
3:輸入七個點座標,前兩個點構成一條直線,後五個點構成一個凸五邊形、凸四邊形或凸三角形,輸出直線與五邊形、四邊形或三角形相交的交點數量。如果交點有兩個,再按面積從小到大輸出被直線分割成兩部分的面積(不換行)。若直線與多邊形形的一條邊線重合,輸出"The line is coincide with one of the lines"。若後五個點不符合五邊形輸入,若前兩點重合,輸出"points coincide"。
以上3選項中,若輸入的點無法構成多邊形,則輸出"not a polygon"。輸入的五個點座標可能存在冗餘,假設多邊形一條邊上兩個端點分別是x、y,邊線中間有一點z,另一頂點s:
1)符合要求的輸入:頂點重複或者z與xy都相鄰,如:x x y s、x z y s、x y x s、s x y y。此時去除冗餘點,保留一個x、一個y。
2) 不符合要求的輸入:z不與xy都相鄰,如:z x y s、x z s y、x s z y
import java.util.Scanner;
class Point
{
double x;
double y;
int exist=1;//1:存在0:不存在2:交點無數個
int flag=0;
public boolean pointchonghe(Point A,Point B)//判斷兩點重合
{
if(A.x==B.x&&A.y==B.y)
return true;
else
return false;
}
public boolean Pointscoincide(Point A,Point B,Point C,Point D)//判斷四邊形四點重合
{
if(A.x==B.x&&A.y==B.y||A.x==C.x&&A.y==C.y||A.x==D.x&&A.y==D.y||B.x==C.x&&B.y==C.y||B.x==D.x&&B.y==D.y||C.x==D.x&&C.y==D.y)
return true;
else
return false;
}
}
//==========================================================================================================
class Line
{
Point p1=new Point();
Point p2=new Point();
double a;
double b;
double c;
double D;//線段距離
public void L(Line l)//一般式係數
{
l.a=l.p2.y-l.p1.y;
l.b=l.p1.x-l.p2.x;
l.c=l.p2.x*l.p1.y-l.p1.x*l.p2.y;
}
public void distanse(Line l)//求線段距離D
{
l.D=Math.sqrt(Math.pow(l.p1.x-l.p2.x,2)+Math.pow(l.p1.y-l.p2.y,2));
l.D=Math.round(l.D*1000000000)/(double)1000000000;
}
public void D(Point p1,Point p2,Line lp1p2)//兩點間距離
{
lp1p2.D=Math.sqrt(Math.pow(lp1p2.p1.x-lp1p2.p2.x,2)+Math.pow(lp1p2.p1.y-lp1p2.p2.y,2));
lp1p2.D=Math.round(lp1p2.D*1000000000)/(double)1000000000;
}
public boolean zhixian(Point X,Line l)//點是否在直線上
{
L(l);
if(l.a*X.x+l.b*X.y+l.c==0)
return true;
else
return false;
}
public boolean pingxing(Line l1,Line l2)//判斷是否平行(有無交點)
{
L(l1);
L(l2);
if(l1.b==0&&l2.b==0)
return true;
else if(l1.b!=0&&l2.b!=0&&(l1.a/l1.b==l2.a/l2.b))
return true;
else
return false;
}
public boolean linechonghe(Line l1,Line l2)//判斷是否兩線重合
{
L(l1);
L(l2);
if(l1.b==0&&l2.b==0)
{
if(l1.c/l1.a==l2.c/l2.a)
return true;
else
return false;
}
else if(l1.a==0&&l2.a==0)
{
if(l1.c/l1.b==l2.c/l2.b)
return true;
else
return false;
}
else
{
if(l1.c/l1.a==l2.c/l2.a&&l1.c/l1.b==l2.c/l2.b)
return true;
else
return false;
}
}
public void jiaodian(Line l1,Line l2,Point O)//兩條直線交點
{
if(l1.pingxing(l1,l2))
{
O.exist=0;
//System.out.println("@@@@@@@@");
}
else
{
l1.L(l1);
l2.L(l2);
O.x=(l1.b*l2.c-l2.b*l1.c)/(l1.a*l2.b-l2.a*l1.b);
O.y=(l2.a*l1.c-l1.a*l2.c)/(l1.a*l2.b-l2.a*l1.b);
O.x=Math.round(O.x*1000000000)/(double)1000000000;
O.y=Math.round(O.y*1000000000)/(double)1000000000;
}
}
public boolean pointwhere(Point A,Point B,Point C,Line lBC)//點A是否線上段BC上(含端點)
{
if(A.pointchonghe(A,B)||A.pointchonghe(A,C))
return true;
else
{
Line lAB=new Line();
lAB.p1=A;
lAB.p2=B;
Line lAC=new Line();
lAC.p1=A;
lAC.p2=C;
lAB.D(A,B,lAB);
lAC.D(A,C,lAC);
lBC.D(B,C,lBC);
if(lAB.D+lAC.D-lBC.D<0.000001)
return true;
else
return false;
}
}
public boolean pointwhere1(Point A,Point B,Point C,Line lBC)//點A是否線上段BC上(不含端點)
{
if(A.pointchonghe(A,B)||A.pointchonghe(A,C))
return false;
else
{
Line lAB=new Line();
lAB.p1=A;
lAB.p2=B;
Line lAC=new Line();
lAC.p1=A;
lAC.p2=C;
lAB.D(A,B,lAB);
lAC.D(A,C,lAC);
lBC.D(B,C,lBC);
if(lAB.D+lAC.D-lBC.D<0.000001)
return true;
else
return false;
}
}
}
//=======================================================================================================
class Triangle
{
Point p1=new Point();
Point p2=new Point();
Point p3=new Point();
Line l1=new Line();
Line l2=new Line();
Line l3=new Line();
double S;//面積
int num;//交點數量
int flag=0;//0:不存在/1-10:10種三角形組合
public void Set(Point A,Point B,Point C,Triangle T)
{
T.p1=A;
T.p2=B;
T.p3=C;
}
public void Line(Point A,Point B,Point C,Triangle T)//newLine
{
T.l1.p1=A;
T.l1.p2=B;
T.l2.p1=B;
T.l2.p2=C;
T.l3.p1=A;
T.l3.p2=C;
}
public boolean sanjiaox(Point A,Point B,Point C,Triangle T)//判斷是否為三角形
{
T.Line(A,B,C,T);
l1.distanse(l1);
l2.distanse(l2);
l3.distanse(l3);
if((l1.D+l2.D>l3.D&&l1.D<=l3.D&&l2.D<=l3.D)||(l1.D+l3.D>l2.D&&l1.D<=l2.D&&l3.D<=l2.D)||(l2.D+l3.D>l1.D&&l2.D<=l1.D&&l2.D<=l1.D))
return true;
else
return false;
}
public void sanjiaoxmianji(Triangle t)//三角形面積
{
t.Line(t.p1,t.p2,t.p3,t);
t.l1.distanse(t.l1);
t.l2.distanse(t.l2);
t.l3.distanse(t.l3);
double x=(t.l1.D+t.l2.D+t.l3.D)/2;
t.S=Math.sqrt(x*(x-t.l1.D)*(x-t.l2.D)*(x-t.l3.D));
}
public void xiaomianji(Point P1,Point P2,Point P3,Triangle t,Triangle T)//切割小三角形面積
{
if(P1.flag==1&&P2.flag==1)//三角形CP1P2
{
t.p1=T.p2;
t.p2=P1;
t.p3=P2;
t.sanjiaoxmianji(t);
}
else if(P1.flag==1&&P3.flag==1)
{
t.p1=T.p1;
t.p2=P1;
t.p3=P3;
t.sanjiaoxmianji(t);
}
else if(P2.flag==1&&P3.flag==1)
{
t.p1=T.p3;
t.p2=P2;
t.p3=P3;
t.sanjiaoxmianji(t);
}
}
public void whichTriangle(Point A,Point B,Point C,Point D,Point E,Triangle tABC,Triangle tABD,Triangle tABE,Triangle tACD,Triangle tACE,Triangle tADE,Triangle tBCD,Triangle tBCE,Triangle tBDE,Triangle tCDE)//判斷是哪種三角形
{
if(tABC.sanjiaox(A,B,C,tABC))
{
Line lCD=new Line();
lCD.p1=C;
lCD.p2=D;
Line lCE=new Line();
lCE.p1=C;
lCE.p2=E;
lCD.D(C,D,lCD);
lCE.D(C,E,lCE);
if(tABC.l3.pointwhere(D,A,C,tABC.l3)&&tABC.l3.pointwhere(E,A,C,tABC.l3)&&lCD.D<=lCE.D)
tABC.flag=1;
else if((tABC.l3.pointwhere(D,A,C,tABC.l3)||D.pointchonghe(D,B))&&(tABC.l3.pointwhere(E,A,C,tABC.l3)||E.pointchonghe(E,B))&&(!tABC.l3.pointwhere(D,A,C,tABC.l3)&&!tABC.l3.pointwhere(E,A,C,tABC.l3)))
tABC.flag=1;
}
if(tABD.sanjiaox(A,B,D,tABD))
{
if((tABD.l2.pointwhere(C,B,D,tABD.l2)||C.pointchonghe(C,A))&&(tABD.l3.pointwhere(E,A,D,tABD.l3)||E.pointchonghe(E,B)))
tABD.flag=1;
}
if(tABE.sanjiaox(A,B,E,tABE))
{
Line lBC=new Line();
lBC.p1=B;
lBC.p2=C;
Line lBD=new Line();
lBD.p1=B;
lBD.p2=D;
lBC.D(B,C,lBC);
lBD.D(B,D,lBD);
if(tABE.l2.pointwhere(C,B,E,tABE.l2)&&tABE.l2.pointwhere(D,B,E,tABE.l2)&&lBC.D<=lBD.D)
tABE.flag=1;
else if((tABE.l2.pointwhere(C,B,E,tABE.l2)||C.pointchonghe(C,A))&&(tABE.l2.pointwhere(D,B,E,tABE.l2)||D.pointchonghe(D,A))&&(!tABE.l2.pointwhere(C,B,E,tABE.l2)&&!tABE.l2.pointwhere(D,B,E,tABE.l2)))
tABE.flag=1;
}
if(tACD.sanjiaox(A,C,D,tACD))
{
if((tACD.l1.pointwhere(B,A,C,tACD.l1)||B.pointchonghe(B,D))&&(tACD.l3.pointwhere(E,A,D,tACD.l3)||E.pointchonghe(E,C)))
tACD.flag=1;
}
if(tACE.sanjiaox(A,C,E,tACE))
{
if((tACE.l1.pointwhere(B,A,C,tACE.l1)||B.pointchonghe(B,E))&&(tACE.l2.pointwhere(D,C,E,tACE.l2)||D.pointchonghe(D,A)))
tACE.flag=1;
}
if(tADE.sanjiaox(A,D,E,tADE))
{
Line lAB=new Line();
lAB.p1=A;
lAB.p2=B;
Line lAC=new Line();
lAC.p1=A;
lAC.p2=C;
lAB.D(A,B,lAB);
lAC.D(A,C,lAC);
if(tADE.l1.pointwhere(B,A,D,tADE.l1)&&tADE.l1.pointwhere(C,A,D,tADE.l1)&&lAB.D<=lAC.D)
tADE.flag=1;
else if((tADE.l1.pointwhere(B,A,D,tADE.l1)||B.pointchonghe(B,E))&&(tADE.l1.pointwhere(C,A,D,tADE.l1)||C.pointchonghe(C,E))&&(!tADE.l1.pointwhere(B,A,D,tADE.l1)&&!tADE.l1.pointwhere(C,A,D,tADE.l1)))
tADE.flag=1;
}
if(tBCD.sanjiaox(B,C,D,tBCD))
{
Line lBA=new Line();
lBA.p1=B;
lBA.p2=A;
Line lBE=new Line();
lBE.p1=B;
lBE.p2=E;
lBA.D(B,A,lBA);
lBE.D(B,E,lBE);
if(tBCD.l3.pointwhere(A,B,D,tBCD.l3)&&tBCD.l3.pointwhere(E,B,D,tBCD.l3)&&lBA.D<=lBE.D)
tBCD.flag=1;
else if((tBCD.l3.pointwhere(A,B,D,tBCD.l3)||A.pointchonghe(A,C))&&(tBCD.l3.pointwhere(E,B,D,tBCD.l3)||E.pointchonghe(E,C))&&(!tBCD.l3.pointwhere(A,B,D,tBCD.l3)&&!tBCD.l3.pointwhere(E,B,D,tBCD.l3)))
{
tBCD.flag=1;
System.out.println("###");
}
}
if(tBCE.sanjiaox(B,C,E,tBCE))
{
if((tBCE.l3.pointwhere(A,B,E,tBCE.l3)||A.pointchonghe(A,C))&&(tBCE.l2.pointwhere(D,C,E,tBCE.l2)||D.pointchonghe(D,B)))
tBCE.flag=1;
}
if(tBDE.sanjiaox(B,D,E,tBDE))
{
if((tBDE.l1.pointwhere(C,B,D,tBDE.l1)||C.pointchonghe(C,E))&&(tBDE.l3.pointwhere(A,B,E,tBDE.l3)||A.pointchonghe(A,D)))
tBDE.flag=1;
}
if(tCDE.sanjiaox(C,D,E,tCDE))
{
Line lCA=new Line();
lCA.p1=C;
lCA.p2=A;
Line lCB=new Line();
lCB.p1=C;
lCB.p2=B;
lCA.D(C,A,lCA);
lCB.D(C,B,lCB);
if(tCDE.l3.pointwhere(A,C,E,tCDE.l3)&&tCDE.l3.pointwhere(B,C,E,tCDE.l3)&&lCB.D<=lCA.D)
tCDE.flag=1;
else if((tCDE.l3.pointwhere(B,C,E,tCDE.l3)||A.pointchonghe(A,D))&&(tCDE.l3.pointwhere(B,C,E,tCDE.l3)||B.pointchonghe(B,D))&&(!tCDE.l3.pointwhere(A,C,E,tCDE.l3)&&!tCDE.l3.pointwhere(B,C,E,tCDE.l3)))
tCDE.flag=1;
}
}
public void jiaodiannum(Point P1,Point P2,Point P3,Line lAB,Triangle t)//交點數(線和三角形)
{
t.num=0;
P1.flag=0;
P2.flag=0;
P3.flag=0;
t.Line(t.p1,t.p2,t.p3,t);
lAB.jiaodian(lAB,t.l1,P1);
if(P1.exist==1&&t.l1.pointwhere(P1, t.l1.p1, t.l1.p2,t.l1))
{
t.num++;
P1.flag=1;//交點線上段上
}
lAB.jiaodian(lAB,t.l2,P2);
if(P2.exist==1&&t.l2.pointwhere(P2,t.l2.p1,t.l2.p2,t.l2))
{
if(P1.flag==0||(!P1.pointchonghe(P1,P2)&&P1.flag==1))
{
t.num++;
P2.flag=1;
}
}
lAB.jiaodian(lAB,t.l3,P3);
if(P3.exist==1&&t.l3.pointwhere(P3,t.l3.p1,t.l3.p2,t.l3))
{
if(P1.flag==0&&P2.flag==0)
{
t.num++;
P3.flag=1;
}
else if(P1.flag==1&&P2.flag==0&&!P1.pointchonghe(P1,P3))
{
t.num++;
P3.flag=1;
}
else if(P1.flag==0&&P2.flag==1&&!P2.pointchonghe(P2,P3))
{
t.num++;
P3.flag=1;
}
}
}
public void function3(Point A,Point B,Point P1,Point P2,Point P3,Line lAB,Triangle T)//三角形
{
if(A.pointchonghe(A,B))
{
System.out.print("points coincide");return;
}
T.Line(T.p1,T.p2,T.p3,T);
if(lAB.linechonghe(lAB,T.l1)||lAB.linechonghe(lAB,T.l2)||lAB.linechonghe(lAB,T.l3))
{
System.out.print("The line is coincide with one of the lines");return;
}
T.jiaodiannum(P1,P2,P3,lAB,T);
System.out.print(T.num);
if(T.num==2)
{
System.out.print(" ");
T.sanjiaoxmianji(T);
Triangle t=new Triangle();
T.xiaomianji(P1,P2,P3,t,T);//切割小三角形面積
double s=T.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
}
}
//==================================================================================================
class Quadrilateral
{
Point p1=new Point();
Point p2=new Point();
Point p3=new Point();
Point p4=new Point();
Line l1=new Line();
Line l2=new Line();
Line l3=new Line();
Line l4=new Line();
Line l5=new Line();
Line l6=new Line();
double C;//周長
double S;//面積
int num;
int exist=1;//1:存在 0:不存在
int flag=0;
public void Set(Point A,Point B,Point C,Point D,Quadrilateral Q)
{
Q.p1=A;
Q.p2=B;
Q.p3=C;
Q.p4=D;
}
public void Line(Point A,Point B,Point C,Point D,Quadrilateral Q)//newLine
{
Q.l1.p1=A;
Q.l1.p2=B;
Q.l2.p1=B;
Q.l2.p2=C;
Q.l3.p1=C;
Q.l3.p2=D;
Q.l4.p1=A;
Q.l4.p2=D;
Q.l5.p1=B;
Q.l5.p2=D;
Q.l6.p1=A;
Q.l6.p2=C;
}
public boolean Quadrilateral(Point A,Point B,Point C,Point D,Quadrilateral Q)//判斷是否是四邊形
{
Q.Line(A,B,C,D,Q);
if((!Q.l1.zhixian(C,Q.l1))&&(!Q.l1.zhixian(D,Q.l1))&&(!Q.l3.zhixian(A,Q.l3))&&(!Q.l2.zhixian(D,Q.l2))&&(!A.Pointscoincide(A,B,C,D)))
{
Point O=new Point();
Q.l1.jiaodian(Q.l5,Q.l6,O);//AC和BD交點
if(O.exist==1&&(Q.l6.pointwhere(O,A,C,Q.l6)||Q.l5.pointwhere(O,B,D,Q.l5)))//交點線上段AC和BD上
return true;
else
return false;
}
else
return false;
}
public boolean tuQuadrilateral(Point A,Point B,Point C,Point D,Quadrilateral Q)//凸
{
Q.Line(A,B,C,D,Q);
if((!Q.l1.zhixian(C,Q.l1))&&(!Q.l1.zhixian(D,Q.l1))&&(!Q.l3.zhixian(A,Q.l3))&&(!Q.l2.zhixian(D,Q.l2))&&(!A.Pointscoincide(A,B,C,D)))
{
Point O=new Point();
Q.l5.jiaodian(Q.l5,Q.l6,O);//AC和BD交點
if(O.exist==1&&Q.l6.pointwhere(O,A,C,Q.l6)&&Q.l5.pointwhere(O,B,D,Q.l5))//交點線上段AC和BD上
return true;
else
return false;
}
else
return false;
}
public void Quadrilateralmianji(Quadrilateral Q)//凸四邊形面積
{
Q.Line(Q.p1,Q.p2,Q.p3,Q.p4,Q);
Q.l1.distanse(Q.l1);
Q.l2.distanse(Q.l2);
Q.l3.distanse(Q.l3);
Q.l4.distanse(Q.l4);
Q.l5.distanse(Q.l5);
double x1=(l1.D+l4.D+l5.D)/2;
double s1=Math.sqrt(x1*(x1-l1.D)*(x1-l4.D)*(x1-l5.D));
double x2=(l2.D+l3.D+l5.D)/2;
double s2=Math.sqrt(x2*(x2-l2.D)*(x2-l3.D)*(x2-l5.D));
Q.S=s1+s2;
}
public void Quadrilateralmianji1(Point P1,Point P2,Point P3,Point P4,Quadrilateral Q)//四邊形切割小面積
{
Q.Quadrilateralmianji(Q);
if(P1.flag==1&&P2.flag==1)
{
Triangle t=new Triangle();
t.Set(Q.p2,P1,P2,t);
t.sanjiaoxmianji(t);
double s=Q.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P2.flag==1&&P3.flag==1)
{
Triangle t=new Triangle();
t.Set(Q.p3,P2,P3,t);
t.sanjiaoxmianji(t);
double s=Q.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P3.flag==1&&P4.flag==1)
{
Triangle t=new Triangle();
t.Set(Q.p4,P3,P4,t);
t.sanjiaoxmianji(t);
double s=Q.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P1.flag==1&&P4.flag==1)
{
Triangle t=new Triangle();
t.Set(Q.p1,P1,P4,t);
t.sanjiaoxmianji(t);
double s=Q.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P1.flag==1&&P3.flag==1)
{
Triangle t1=new Triangle();
t1.Set(Q.p1,P1,P3,t1);
Triangle t2=new Triangle();
t2.Set(Q.p1,Q.p4,P3,t2);
Triangle t3=new Triangle();
t3.Set(Q.p2,P1,P3,t3);
Triangle t4=new Triangle();
t4.Set(Q.p2,Q.p3,P3,t4);
t1.sanjiaoxmianji(t1);
t2.sanjiaoxmianji(t2);
t3.sanjiaoxmianji(t3);
t4.sanjiaoxmianji(t4);
double s1=t1.S+t2.S;
double s2=t3.S+t4.S;
if(s1<s2)
System.out.print(Math.round(s1*1000)/(double)1000+" "+Math.round(s2*1000)/(double)1000);
else
System.out.print(Math.round(s2*1000)/(double)1000+" "+Math.round(s1*1000)/(double)1000);
}
else if(P2.flag==1&&P4.flag==1)
{
Triangle t1=new Triangle();
t1.Set(Q.p1,Q.p2,P2,t1);
Triangle t2=new Triangle();
t2.Set(Q.p1,P2,P4,t2);
Triangle t3=new Triangle();
t3.Set(Q.p3,Q.p4,P2,t3);
Triangle t4=new Triangle();
t4.Set(Q.p4,P2,P4,t4);
t1.sanjiaoxmianji(t1);
t2.sanjiaoxmianji(t2);
t3.sanjiaoxmianji(t3);
t4.sanjiaoxmianji(t4);
double s1=t1.S+t2.S;
double s2=t3.S+t4.S;
if(s1<s2)
System.out.print(Math.round(s1*1000)/(double)1000+" "+Math.round(s2*1000)/(double)1000);
else
System.out.print(Math.round(s2*1000)/(double)1000+" "+Math.round(s1*1000)/(double)1000);
}
}
public boolean PointQuadrilateral(Point E,Point A,Point B,Point C,Point D,Quadrilateral QABCD)//判斷點在四邊形內部還是外部
{
QABCD.Quadrilateralmianji(QABCD);
Triangle tEAB=new Triangle();
tEAB.p1=E;
tEAB.p2=A;
tEAB.p3=B;
Triangle tEBC=new Triangle();
tEBC.p1=E;
tEBC.p2=B;
tEBC.p3=C;
Triangle tECD=new Triangle();
tECD.p1=E;
tECD.p2=C;
tECD.p3=D;
Triangle tEAD=new Triangle();
tEAD.p1=E;
tEAD.p2=A;
tEAD.p3=D;
tEAB.sanjiaoxmianji(tEAB);
tEBC.sanjiaoxmianji(tEBC);
tECD.sanjiaoxmianji(tECD);
tEAD.sanjiaoxmianji(tEAD);
double S=tEAB.S+tEBC.S+tECD.S+tEAD.S;
if(S-QABCD.S<0.0001)
return true;
else
return false;
}
public void whichQuadrilateral(Point A,Point B,Point C,Point D,Point E,Quadrilateral QABCD,Quadrilateral QABCE,Quadrilateral QABDE,Quadrilateral QACDE,Quadrilateral QBCDE)//判斷構成哪種四邊形
{
if(QABCD.tuQuadrilateral(A,B,C,D,QABCD))//四邊形QABCD(判斷E點位置)
{
QABCD.Line(A,B,C,D,QABCD);
if(QABCD.l4.pointwhere(E,A,D,QABCD.l4)||E.pointchonghe(E,B)||E.pointchonghe(E,C))//
QABCD.flag=1;
}
if(QABCE.tuQuadrilateral(A,B,C,E,QABCE))
{
QABCE.Line(A,B,C,E,QABCE);
if(QABCE.l3.pointwhere(D,C,E,QABCE.l3)||D.pointchonghe(D,A)||D.pointchonghe(D,B))//
QABCE.flag=1;
}
if(QABDE.tuQuadrilateral(A,B,D,E,QABDE))
{
QABDE.Line(A,B,D,E,QABDE);
if(QABDE.l2.pointwhere(C,B,D,QABDE.l2)||C.pointchonghe(C,A)||C.pointchonghe(C,E))//
QABDE.flag=1;
}
if(QACDE.tuQuadrilateral(A,C,D,E,QACDE))
{
QACDE.Line(A,C,D,E,QACDE);
if(QACDE.l1.pointwhere(B,A,C,QACDE.l1)||B.pointchonghe(B,E)||B.pointchonghe(B,D))//
QACDE.flag=1;
}
if(QBCDE.tuQuadrilateral(B,C,D,E,QBCDE))
{
QBCDE.Line(B,C,D,E,QBCDE);
if(QBCDE.l4.pointwhere(A,B,E,QBCDE.l4)||A.pointchonghe(A,C)||A.pointchonghe(A,D))//
QBCDE.flag=1;
}
}
public void Quadrilateralnum(Point P1,Point P2,Point P3,Point P4,Line lAB,Quadrilateral Q)//交點數(線和四邊形)
{
Q.num=0;
P1.flag=0;
P2.flag=0;
P3.flag=0;
P4.flag=0;
Q.Line(Q.p1,Q.p2,Q.p3,Q.p4,Q);
lAB.jiaodian(lAB,Q.l1,P1);
if(P1.exist==1&&Q.l1.pointwhere(P1,Q.p1,Q.p2,Q.l1))
{
Q.num++;
P1.flag=1;//交點線上段上
}
lAB.jiaodian(lAB,Q.l2,P2);
if(P2.exist==1&&Q.l2.pointwhere(P2,Q.p2,Q.p3,Q.l2))
{
if(P1.flag==0||(!P1.pointchonghe(P1,P2)&&P1.flag==1))
{
Q.num++;
P2.flag=1;
}
}
lAB.jiaodian(lAB,Q.l3,P3);
if(P3.exist==1&&Q.l3.pointwhere(P3,Q.p3,Q.p4,Q.l3))
{
if(P1.flag==0&&P2.flag==0)
{
Q.num++;
P3.flag=1;
}
else if(P1.flag==1&&(P2.flag==0&&!P1.pointchonghe(P1,P3)))
{
Q.num++;
P3.flag=1;
}
else if(P1.flag==0&&(P2.flag==1&&!P2.pointchonghe(P2,P3)))
{
Q.num++;
P3.flag=1;
}
}
lAB.jiaodian(lAB,Q.l4,P4);
if(P4.exist==1&&Q.l1.pointwhere(P4,Q.l4.p1,Q.l4.p2,Q.l4))
{
if(P1.flag==0&&P2.flag==0&&P3.flag==0)
{
Q.num++;
P4.flag=1;
}
else if(P1.flag==1&&P2.flag==0&&P3.flag==0&&!P1.pointchonghe(P1,P4))
{
Q.num++;
P4.flag=1;
}
else if(P1.flag==0&&P2.flag==1&&P3.flag==0&&!P2.pointchonghe(P2,P4))
{
Q.num++;
P4.flag=1;
}
else if(P1.flag==0&&P2.flag==0&&P3.flag==1&&!P3.pointchonghe(P3,P4))
{
Q.num++;
P4.flag=1;
}
}
}
public void function4(Point A,Point B,Point P1,Point P2,Point P3,Point P4,Line lAB,Quadrilateral Q)
{
if(A.pointchonghe(A,B))
{
System.out.print("points coincide");return;
}
Q.Line(Q.p1,Q.p2,Q.p3,Q.p4,Q);
if(lAB.linechonghe(lAB,Q.l1)||lAB.linechonghe(lAB,Q.l2)||lAB.linechonghe(lAB,Q.l3)||lAB.linechonghe(lAB,Q.l4))
{
System.out.print("The line is coincide with one of the lines");return;
}
Q.Quadrilateralnum(P1,P2,P3,P4,lAB,Q);
System.out.print(Q.num);
if(Q.num==2)
{
System.out.print(" ");
Q.Quadrilateralmianji1(P1,P2,P3,P4,Q);
}
}
}
//=======================================================================================================
class Polygon
{
Point p1=new Point();
Point p2=new Point();
Point p3=new Point();
Point p4=new Point();
Point p5=new Point();
Line l1=new Line();
Line l2=new Line();
Line l3=new Line();
Line l4=new Line();
Line l5=new Line();
double C;
double S;
int num;
int exist=0;
public void Set(Point A,Point B,Point C,Point D,Point E,Polygon P)
{
P.p1=A;
P.p2=B;
P.p3=C;
P.p4=D;
P.p5=E;
}
public void Line(Point A,Point B,Point C,Point D,Point E,Polygon P)
{
P.l1.p1=A;
P.l1.p2=B;
P.l2.p1=B;
P.l2.p2=C;
P.l3.p1=C;
P.l3.p2=D;
P.l4.p1=D;
P.l4.p2=E;
P.l5.p1=A;
P.l5.p2=E;
}
public void C(Polygon P)//周長
{
P.Line(P.p1,P.p2,P.p3,P.p4,P.p5,P);
P.l1.distanse(P.l1);
P.l2.distanse(P.l2);
P.l3.distanse(P.l3);
P.l4.distanse(P.l4);
P.l5.distanse(P.l5);
P.C=P.l1.D+P.l2.D+P.l3.D+P.l4.D+P.l5.D;
}
public void S(Polygon P)//面積
{
P.Line(P.p1,P.p2,P.p3,P.p4,P.p5,P);
P.l1.distanse(P.l1);
P.l2.distanse(P.l2);
P.l3.distanse(P.l3);
P.l4.distanse(P.l4);
P.l5.distanse(P.l5);
Triangle tABC=new Triangle();
tABC.Set(P.p1,P.p2,P.p3,tABC);
Triangle tACD=new Triangle();
tACD.Set(P.p1,P.p3,P.p4,tACD);
Triangle tADE=new Triangle();
tADE.Set(P.p1,P.p4,P.p5,tADE);
tABC.sanjiaoxmianji(tABC);
tACD.sanjiaoxmianji(tACD);
tADE.sanjiaoxmianji(tADE);
P.S=tABC.S+tACD.S+tADE.S;
}
public boolean Polygon(Point A,Point B,Point C,Point D,Point E,Quadrilateral QABCD,Quadrilateral QABCE,Quadrilateral QABDE,Quadrilateral QACDE,Quadrilateral QBCDE,Polygon P)//判斷是五邊形
{
Point O1=new Point();
Point O2=new Point();
Point O3=new Point();
Point O4=new Point();
Point O5=new Point();
Point O6=new Point();
P.Line(A,B,C,D,E,P);
if(QABCD.Quadrilateral(A,B,C,D,QABCD))
{
//AE,DE
P.l5.jiaodian(P.l5,QABCD.l1,O1);
P.l5.jiaodian(P.l5,QABCD.l2,O2);
P.l5.jiaodian(P.l5,QABCD.l3,O3);
P.l4.jiaodian(P.l4,QABCD.l1,O4);
P.l4.jiaodian(P.l4,QABCD.l2,O5);
P.l4.jiaodian(P.l4,QABCD.l3,O6);
if(
((O1.exist==1&&!P.l5.pointwhere1(O1,A,E,P.l5))||O1.exist!=1)&&
((O2.exist==1&&!P.l5.pointwhere(O2,A,E,P.l5))||O2.exist!=1)&&
((O3.exist==1&&!P.l5.pointwhere(O3,A,E,P.l5))||O3.exist!=1)&&
((O4.exist==1&&!P.l4.pointwhere(O4,D,E,P.l4))||O4.exist!=1)&&
((O5.exist==1&&!P.l4.pointwhere(O5,D,E,P.l4))||O5.exist!=1)&&
((O6.exist==1&&!P.l4.pointwhere1(O6,D,E,P.l4))||O6.exist!=1)
)
return true;
else
{
QABCD.exist=0;
return false;
}
}
else if(QABCE.Quadrilateral(A,B,C,E,QABCE))
{
//CD,DE
P.l3.jiaodian(P.l3,QABCE.l1,O1);
P.l3.jiaodian(P.l3,QABCE.l2,O2);
P.l3.jiaodian(P.l3,QABCE.l4,O3);
P.l4.jiaodian(P.l4,QABCE.l1,O4);
P.l4.jiaodian(P.l4,QABCE.l2,O5);
P.l4.jiaodian(P.l4,QABCE.l4,O6);
if(
((O1.exist==1&&!P.l3.pointwhere(O1,C,D,P.l3))||O1.exist!=1)&&
((O2.exist==1&&!P.l3.pointwhere1(O2,C,D,P.l3))||O2.exist!=1)&&
((O3.exist==1&&!P.l3.pointwhere(O3,C,D,P.l3))||O3.exist!=1)&&
((O4.exist==1&&!P.l4.pointwhere(O4,D,E,P.l4))||O4.exist!=1)&&
((O5.exist==1&&!P.l4.pointwhere(O5,D,E,P.l4))||O5.exist!=1)&&
((O6.exist==1&&!P.l4.pointwhere1(O6,D,E,P.l4))||O6.exist!=1)
)
return true;
else
{
QABCE.exist=0;
return false;
}
}
else if(QABDE.Quadrilateral(A,B,D,E,QABDE))
{
//BC,CD
P.l2.jiaodian(P.l2,QABDE.l1,O1);
P.l2.jiaodian(P.l2,QABDE.l3,O2);
P.l2.jiaodian(P.l2,QABDE.l4,O3);
P.l3.jiaodian(P.l3,QABDE.l1,O4);
P.l3.jiaodian(P.l3,QABDE.l3,O5);
P.l3.jiaodian(P.l3,QABDE.l4,O6);
if(
((O1.exist==1&&!P.l2.pointwhere1(O1,B,C,P.l2))||O1.exist!=1)&&
((O2.exist==1&&!P.l2.pointwhere(O2,B,C,P.l2))||O2.exist!=1)&&
((O3.exist==1&&!P.l2.pointwhere(O3,B,C,P.l2))||O3.exist!=1)&&
((O4.exist==1&&!P.l3.pointwhere(O4,C,D,P.l3))||O4.exist!=1)&&
((O5.exist==1&&!P.l3.pointwhere1(O5,C,D,P.l3))||O5.exist!=1)&&
((O6.exist==1&&!P.l3.pointwhere(O6,C,D,P.l3))||O6.exist!=1)
)
return true;
else
{
QABDE.exist=0;
return false;
}
}
else if(QACDE.Quadrilateral(A,C,D,E,QACDE))
{
//AB,BC
P.l1.jiaodian(P.l1,QACDE.l2,O1);
P.l1.jiaodian(P.l1,QACDE.l3,O2);
P.l1.jiaodian(P.l1,QACDE.l4,O3);
P.l2.jiaodian(P.l2,QACDE.l2,O4);
P.l2.jiaodian(P.l2,QACDE.l3,O5);
P.l2.jiaodian(P.l2,QACDE.l4,O6);
if(
((O1.exist==1&&!P.l1.pointwhere(O1,A,B,P.l1))||O1.exist!=1)&&
((O2.exist==1&&!P.l1.pointwhere(O2,A,B,P.l1))||O2.exist!=1)&&
((O3.exist==1&&!P.l1.pointwhere1(O3,A,B,P.l1))||O3.exist!=1)&&
((O4.exist==1&&!P.l2.pointwhere(O4,B,C,P.l2))||O4.exist!=1)&&
((O5.exist==1&&!P.l2.pointwhere1(O5,B,C,P.l2))||O5.exist!=1)&&
((O6.exist==1&&!P.l2.pointwhere(O6,B,C,P.l2))||O6.exist!=1)
)
return true;
else
{
QACDE.exist=0;
return false;
}
}
else if(QBCDE.Quadrilateral(B,C,D,E,QBCDE))
{
//AB,AE
P.l1.jiaodian(P.l1,QBCDE.l1,O1);
P.l1.jiaodian(P.l1,QBCDE.l2,O2);
P.l1.jiaodian(P.l1,QBCDE.l3,O3);
P.l5.jiaodian(P.l5,QBCDE.l1,O4);
P.l5.jiaodian(P.l5,QBCDE.l2,O5);
P.l5.jiaodian(P.l5,QBCDE.l3,O6);
if(
((O1.exist==1&&!P.l1.pointwhere1(O1,A,B,P.l1))||O1.exist!=1)&&
((O2.exist==1&&!P.l1.pointwhere(O2,A,B,P.l1))||O2.exist!=1)&&
((O3.exist==1&&!P.l1.pointwhere(O3,A,B,P.l1))||O3.exist!=1)&&
((O4.exist==1&&!P.l5.pointwhere(O4,A,E,P.l5))||O4.exist!=1)&&
((O5.exist==1&&!P.l5.pointwhere(O5,A,E,P.l5))||O5.exist!=1)&&
((O6.exist==1&&!P.l5.pointwhere1(O6,A,E,P.l5))||O6.exist!=1)
)
return true;
else
{
QBCDE.exist=0;
return false;
}
}
else
{
QABCD.exist=0;
QABCE.exist=0;
QABDE.exist=0;
QACDE.exist=0;
QBCDE.exist=0;
return false;
}
}
public boolean aotuPolygon(Point A,Point B,Point C,Point D,Point E,Quadrilateral QABCD,Quadrilateral QABCE,Quadrilateral QABDE,Quadrilateral QACDE,Quadrilateral QBCDE,Polygon P)//判斷true凹五邊形false凸五邊形
{
if(QABCD.exist==1&&QABCD.PointQuadrilateral(E,A,B,C,D,QABCD)||
QABCE.exist==1&&QABCE.PointQuadrilateral(D,A,B,C,E,QABCE)||
QABDE.exist==1&&QABDE.PointQuadrilateral(C,A,B,D,E,QABDE)||
QACDE.exist==1&&QACDE.PointQuadrilateral(B,A,C,D,E,QACDE)||
QBCDE.exist==1&&QBCDE.PointQuadrilateral(A,B,C,D,E,QBCDE))
return true;
else
return false;
}
public void WHICH(Point A,Point B,Point C,Point D,Point E,Triangle tABC,Triangle tABD,Triangle tABE,Triangle tACD,Triangle tACE,Triangle tADE,Triangle tBCD,Triangle tBCE,Triangle tBDE,Triangle tCDE,Quadrilateral QABCD,Quadrilateral QABCE,Quadrilateral QABDE,Quadrilateral QACDE,Quadrilateral QBCDE,Polygon P)//判斷是凸五邊形/凸四邊形/凸三角形
{
if(Polygon(A,B,C,D,E,QABCD,QABCE,QABDE,QACDE,QBCDE,P)&&!aotuPolygon(A,B,C,D,E,QABCD,QABCE,QABDE,QACDE,QBCDE,P))//五邊形&&不是凹五邊形
P.exist=1;
QABCD.whichQuadrilateral(A,B,C,D,E,QABCD,QABCE,QABDE,QACDE,QBCDE);//判斷哪種四邊形
tABC.whichTriangle(A,B,C,D,E,tABC,tABD,tABE,tACD,tACE,tADE,tBCD,tBCE,tBDE,tCDE);//判斷哪種三角形
}
public void Polygonnum(Point P1,Point P2,Point P3,Point P4,Point P5,Line lAB,Polygon P)//直線與五邊形交點個數
{
P.num=0;
P1.flag=0;
P2.flag=0;
P3.flag=0;
P4.flag=0;
P5.flag=0;
P.Line(P.p1,P.p2,P.p3,P.p4,P.p5,P);
lAB.jiaodian(lAB,P.l1,P1);
if(P1.exist==1&&P.l1.pointwhere(P1,P.p1,P.p2,P.l1))
{
P.num++;
P1.flag=1;
}
lAB.jiaodian(lAB,P.l2,P2);
if(P2.exist==1&&P.l2.pointwhere(P2,P.p2,P.p3,P.l2))
{
if(P1.flag==0||(!P1.pointchonghe(P1,P2)&&P1.flag==1))
{
P.num++;
P2.flag=1;
}
}
lAB.jiaodian(lAB,P.l3,P3);
if(P3.exist==1&&P.l3.pointwhere(P3,P.p3,P.p4,P.l3))
{
if(P1.flag==0&&P2.flag==0)
{
P.num++;
P3.flag=1;
}
else if(P1.flag==1&&P2.flag==0&&!P1.pointchonghe(P1,P3))
{
P.num++;
P3.flag=1;
}
else if(P1.flag==0&&P2.flag==1&&!P2.pointchonghe(P2,P3))
{
P.num++;
P3.flag=1;
}
}
lAB.jiaodian(lAB,P.l4,P4);
if(P4.exist==1&&P.l4.pointwhere(P4,P.p4,P.p5,P.l4))
{
if(P1.flag==0&&P2.flag==0&&P3.flag==0)
{
P.num++;
P4.flag=1;
}
else if(P1.flag==1&&P2.flag==0&&P3.flag==0&&!P1.pointchonghe(P1,P4))
{
P.num++;
P4.flag=1;
}
else if(P1.flag==0&&P2.flag==1&&P3.flag==0&&!P2.pointchonghe(P2,P4))
{
P.num++;
P4.flag=1;
}
else if(P1.flag==0&&P2.flag==0&&P3.flag==1&&!P3.pointchonghe(P3,P4))
{
P.num++;
P4.flag=1;
}
}
lAB.jiaodian(lAB,P.l5,P5);
if(P5.exist==1&&P.l5.pointwhere(P5,P.p1,P.p5,P.l5))
{
if(P1.flag==0&&P2.flag==0&&P3.flag==0&&P4.flag==0)
{
P.num++;
P5.flag=1;
}
else if(P1.flag==1&&P2.flag==0&&P3.flag==0&&P4.flag==0&&!P1.pointchonghe(P1,P5))
{
P.num++;
P5.flag=1;
}
else if(P1.flag==0&&P2.flag==1&&P3.flag==0&&P4.flag==0&&!P2.pointchonghe(P2,P5))
{
P.num++;
P5.flag=1;
}
else if(P1.flag==0&&P2.flag==0&&P3.flag==1&&P4.flag==0&&!P3.pointchonghe(P3,P5))
{
P.num++;
P5.flag=1;
}
else if(P1.flag==0&&P2.flag==0&&P3.flag==0&&P4.flag==1&&!P4.pointchonghe(P4,P5))
{
P.num++;
P5.flag=1;
}
}
}
public void function5(Point A,Point B,Point P1,Point P2,Point P3,Point P4,Point P5,Line lAB,Polygon PP)
{
if(A.pointchonghe(A,B))
{
System.out.print("points coincide");return;
}
PP.Line(PP.p1,PP.p2,PP.p3,PP.p4,PP.p5,PP);
if(lAB.linechonghe(lAB,PP.l1)||lAB.linechonghe(lAB,PP.l2)||lAB.linechonghe(lAB,PP.l3)||lAB.linechonghe(lAB,PP.l4)||lAB.linechonghe(lAB,PP.l5))
{
System.out.print("The line is coincide with one of the lines");return;
}
PP.Polygonnum(P1,P2,P3,P4,P5,lAB,PP);
System.out.print(PP.num);
if(PP.num==2)
{
PP.S(PP);
System.out.print(" ");
if(P1.flag==1&&P2.flag==1)
{
Triangle t=new Triangle();
PP.xiaomianji(PP.p2,P1,P2,t);
double s=PP.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P2.flag==1&&P3.flag==1)
{
Triangle t=new Triangle();
PP.xiaomianji(PP.p3,P2,P3,t);
double s=PP.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P3.flag==1&&P4.flag==1)
{
Triangle t=new Triangle();
PP.xiaomianji(PP.p4,P3,P4,t);
double s=PP.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P4.flag==1&&P5.flag==1)
{
Triangle t=new Triangle();
PP.xiaomianji(PP.p5,P4,P5,t);
double s=PP.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P1.flag==1&&P5.flag==1)
{
Triangle t=new Triangle();
PP.xiaomianji(PP.p1,P1,P5,t);
double s=PP.S-t.S;
if(t.S<s)
System.out.print(Math.round(t.S*1000)/(double)1000+" "+Math.round(s*1000)/(double)1000);
else
System.out.print(Math.round(s*1000)/(double)1000+" "+Math.round(t.S*1000)/(double)1000);
}
else if(P1.flag==1&&P3.flag==1)
{
Triangle t1=new Triangle();
PP.xiaomianji(PP.p2,PP.p3,P1,t1);
Triangle t2=new Triangle();
PP.xiaomianji(PP.p3,P1,P3,t2);
double s1=t1.S+t2.S;
double s2=PP.S-s1;
if(s1<s2)
System.out.print(Math.round(s1*1000)/(double)1000+" "+Math.round(s2*1000)/(double)1000);
else
System.out.print(Math.round(s2*1000)/(double)1000+" "+Math.round(s1*1000)/(double)1000);
}
else if(P1.flag==1&&P4.flag==1)
{
Triangle t1=new Triangle();
PP.xiaomianji(PP.p1,P1,P2,t1);
Triangle t2=new Triangle();
PP.xiaomianji(PP.p1,PP.p5,P4,t2);
double s1=t1.S+t2.S;
double s2=PP.S-s1;
if(s1<s2)
System.out.print(Math.round(s1*1000)/(double)1000+" "+Math.round(s2*1000)/(double)1000);
else
System.out.print(Math.round(s2*1000)/(double)1000+" "+Math.round(s1*1000)/(double)1000);
}
else if(P2.flag==1&&P4.flag==1)
{
Triangle t1=new Triangle();
PP.xiaomianji(PP.p3,P2,P4,t1);
Triangle t2=new Triangle();
PP.xiaomianji(PP.p3,PP.p4,P4,t2);
double s1=t1.S+t2.S;
double s2=PP.S-s1;
if(s1<s2)
System.out.print(Math.round(s1*1000)/(double)1000+" "+Math.round(s2*1000)/(double)1000);
else
System.out.print(Math.round(s2*1000)/(double)1000+" "+Math.round(s1*1000)/(double)1000);
}
else if(P2.flag==1&&P5.flag==1)
{
Triangle t1=new Triangle();
PP.xiaomianji(PP.p1,PP.p2,P2,t1);
Triangle t2=new Triangle();
PP.xiaomianji(PP.p1,P2,P5,t2);
double s1=t1.S+t2.S;
double s2=PP.S-s1;
if(s1<s2)
System.out.print(Math.round(s1*1000)/(double)1000+" "+Math.round(s2*1000)/(double)1000);
else
System.out.print(Math.round(s2*1000)/(double)1000+" "+Math.round(s1*1000)/(double)1000);
}
else if(P3.flag==1&&P5.flag==1)
{
Triangle t1=new Triangle();
PP.xiaomianji(PP.p4,P3,P5,t1);
Triangle t2=new Triangle();
PP.xiaomianji(PP.p4,PP.p5,P5,t2);
double s1=t1.S+t2.S;
double s2=PP.S-s1;
if(s1<s2)
System.out.print(Math.round(s1*1000)/(double)1000+" "+Math.round(s2*1000)/(double)1000);
else
System.out.print(Math.round(s2*1000)/(double)1000+" "+Math.round(s1*1000)/(double)1000);
}
}
}
public void xiaomianji(Point A,Point B,Point C,Triangle t)
{
t.Set(A,B,C,t);
t.sanjiaoxmianji(t);
}
}
//==============================================================================================
public class Main
{
public static void main(String[] args)
{
Scanner in=new Scanner(System.in);
String a=in.nextLine();
int num=(int)a.charAt(0)-(int)'0';
String[] tokens=a.split(" ");
int length=tokens.length;
for(int i=0;i<length;i++)
{
if(i==0)
{
if(!tokens[i].matches("^\\d:[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?),[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$"))
{
System.out.print("Wrong Format");
return;
}
}
else if(i!=0)
{
if(!tokens[i].matches("^[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?),[+-]?(0|(0\\.\\d+)?|[1-9][0-9]*(\\.\\d+)?)$"))
{
System.out.print("Wrong Format");
return;
}
}
}
if(((num==1||num==2)&&length!=5)||(num==3&&length!=7))
{
System.out.print("wrong number of points");
return;
}
String[] arr=a.split(" |:|,");
Point A=new Point();
Point B=new Point();
Point C=new Point();
Point D=new Point();
Point E=new Point();
A.x=Double.valueOf(arr[1]);
A.y=Double.valueOf(arr[2]);
B.x=Double.valueOf(arr[3]);
B.y=Double.valueOf(arr[4]);
C.x=Double.valueOf(arr[5]);
C.y=Double.valueOf(arr[6]);
D.x=Double.valueOf(arr[7]);
D.y=Double.valueOf(arr[8]);
E.x=Double.valueOf(arr[9]);
E.y=Double.valueOf(arr[10]);
Triangle tABC=new Triangle();
tABC.Set(A,B,C,tABC);
Triangle tABD=new Triangle();
tABD.Set(A,B,D,tABD);
Triangle tABE=new Triangle();
tABE.Set(A,B,E,tABE);
Triangle tACD=new Triangle();
tACD.Set(A,C,D,tACD);
Triangle tACE=new Triangle();
tACE.Set(A,C,E,tACE);
Triangle tADE=new Triangle();
tADE.Set(A,D,E,tADE);
Triangle tBCD=new Triangle();
tBCD.Set(B,C,D,tBCD);
Triangle tBCE=new Triangle();
tBCE.Set(B,C,E,tBCE);
Triangle tBDE=new Triangle();
tBDE.Set(B,D,E,tBDE);
Triangle tCDE=new Triangle();
tCDE.Set(C,D,E,tCDE);
Quadrilateral QABCD=new Quadrilateral();
QABCD.Set(A,B,C,D,QABCD);
Quadrilateral QABCE=new Quadrilateral();
QABCE.Set(A,B,C,E,QABCE);
Quadrilateral QABDE=new Quadrilateral();
QABDE.Set(A,B,D,E,QABDE);
Quadrilateral QACDE=new Quadrilateral();
QACDE.Set(A,C,D,E,QACDE);
Quadrilateral QBCDE=new Quadrilateral();
QBCDE.Set(B,C,D,E,QBCDE);
Polygon P=new Polygon();
P.Set(A,B,C,D,E,P);
switch(num)
{
case 1:
if(P.Polygon(A,B,C,D,E,QABCD,QABCE,QABDE,QACDE,QBCDE,P))
System.out.print("true");
else
System.out.print("false");
break;
case 2:
if(P.Polygon(A,B,C,D,E,QABCD,QABCE,QABDE,QACDE,QBCDE,P))
{
if(P.aotuPolygon(A,B,C,D,E,QABCD,QABCE,QABDE,QACDE,QBCDE,P))
System.out.print("false");
else
{
System.out.print("true ");
P.C(P);//面積周長
P.S(P);
System.out.print(Math.round(P.C*1000)/(double)1000+" "+Math.round(P.S*1000)/(double)1000);
}
}
else
System.out.print("not a pentagon");
break;
case 3:
Point F=new Point();
Point G=new Point();
F.x=Double.valueOf(arr[11]);
F.y=Double.valueOf(arr[12]);
G.x=Double.valueOf(arr[13]);
G.y=Double.valueOf(arr[14]);
Line lAB=new Line();
lAB.p1=A;
lAB.p2=B;
//Triangle tCDE=new Triangle();
//tCDE.p1=C;
//tCDE.p2=D;
//tCDE.p3=E;
Triangle tCDF=new Triangle();
tCDF.Set(C,D,F,tCDF);
Triangle tCDG=new Triangle();
tCDG.Set(C,D,G,tCDG);
Triangle tCEF=new Triangle();
tCEF.Set(C,E,F,tCEF);
Triangle tCEG=new Triangle();
tCEG.Set(C,E,G,tCEG);
Triangle tCFG=new Triangle();
tCFG.Set(C,F,G,tCFG);
Triangle tDEF=new Triangle();
tDEF.Set(D,E,F,tDEF);
Triangle tDEG=new Triangle();
tDEG.Set(D,E,G,tDEG);
Triangle tDFG=new Triangle();
tDFG.Set(D,F,G,tDFG);
Triangle tEFG=new Triangle();
tEFG.Set(E,F,G,tEFG);
Quadrilateral QCDEF=new Quadrilateral();
QCDEF.Set(C,D,E,F,QCDEF);
Quadrilateral QCDEG=new Quadrilateral();
QCDEG.Set(C,D,E,G,QCDEG);
Quadrilateral QCDFG=new Quadrilateral();
QCDFG.Set(C,D,F,G,QCDFG);
Quadrilateral QCEFG=new Quadrilateral();
QCEFG.Set(C,E,F,G,QCEFG);
Quadrilateral QDEFG=new Quadrilateral();
QDEFG.Set(D,E,F,G,QDEFG);
Polygon PP=new Polygon();//五邊形CDEFG
PP.Set(C,D,E,F,G,PP);
Point P1=new Point();
Point P2=new Point();
Point P3=new Point();
Point P4=new Point();
Point P5=new Point();
PP.WHICH(C,D,E,F,G,tCDE,tCDF,tCDG,tCEF,tCEG,tCFG,tDEF,tDEG,tDFG,tEFG,QCDEF,QCDEG,QCDFG,QCEFG,QDEFG,PP);//判斷構成三角形/四邊形/五邊形
if(tCDE.flag==1)
tCDE.function3(A,B,P1,P2,P3,lAB,tCDE);
else if(tCDF.flag==1)
tCDF.function3(A,B,P1,P2,P3,lAB,tCDF);
else if(tCDG.flag==1)
tCDG.function3(A,B,P1,P2,P3,lAB,tCDG);
else if(tCEF.flag==1)
tCEF.function3(A,B,P1,P2,P3,lAB,tCEF);
else if(tCEG.flag==1)
tCEG.function3(A,B,P1,P2,P3,lAB,tCEG);
else if(tCFG.flag==1)
tCFG.function3(A,B,P1,P2,P3,lAB,tCFG);
else if(tDEF.flag==1)
tDEF.function3(A,B,P1,P2,P3,lAB,tDEF);
else if(tDEG.flag==1)
tDEG.function3(A,B,P1,P2,P3,lAB,tDEG);
else if(tDFG.flag==1)
tDFG.function3(A,B,P1,P2,P3,lAB,tDFG);
else if(tEFG.flag==1)
tEFG.function3(A,B,P1,P2,P3,lAB,tEFG);
//四邊形
else if(QCDEF.flag==1)
QCDEF.function4(A,B,P1,P2,P3,P4,lAB,QCDEF);
else if(QCDEG.flag==1)
QCDEG.function4(A,B,P1,P2,P3,P4,lAB,QCDEG);
else if(QCDFG.flag==1)
QCDFG.function4(A,B,P1,P2,P3,P4,lAB,QCDFG);
else if(QCEFG.flag==1)
QCEFG.function4(A,B,P1,P2,P3,P4,lAB,QCEFG);
else if(QDEFG.flag==1)
QDEFG.function4(A,B,P1,P2,P3,P4,lAB,QDEFG);
//五邊形
else if(PP.exist==1)
PP.function5(A,B,P1,P2,P3,P4,P5,lAB,PP);
else
System.out.print("not a polygon");
break;
}
}
}
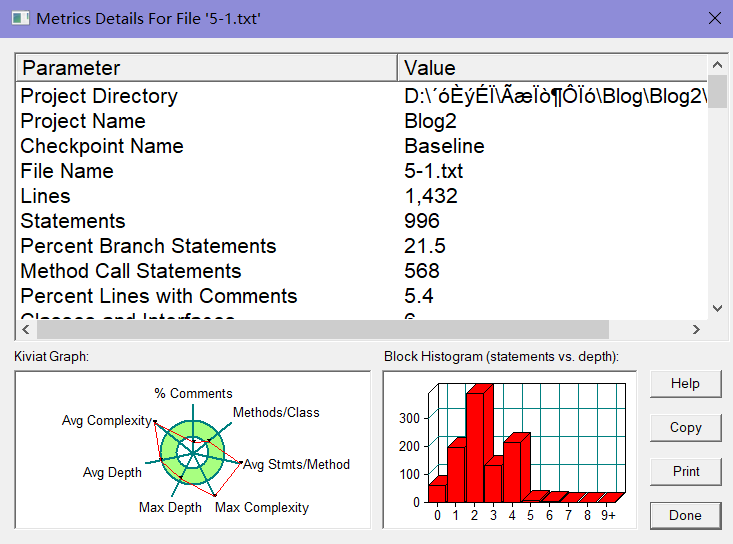
這次在前面的基礎上改了很多,主函數改短了好多,將很多地方歸結到方法中,比之前的好了一點,但依舊不是很好。
但用這個思路和類的結構寫有點費程式碼,整個程式碼格外的長,
現在回過頭去看,確實有很多沒必要的地方,但當時學藝不精,沒有認真去學習,只是憑著自己的想法寫,
在寫下一題是剛寫完一個選項就程式碼長度受限制了,所以只能重來哭唧唧。。
使用者輸入一組選項和資料,進行與五邊形有關的計算。
以下五邊形頂點的座標要求按順序依次輸入,連續輸入的兩個頂點是相鄰頂點,第一個和最後一個輸入的頂點相鄰。
選項包括:
4:輸入十個點座標,前、後五個點分別構成一個凸多邊形(三角形、四邊形、五邊形),判斷它們兩個之間是否存在包含關係(一個多邊形有一條或多條邊與另一個多邊形重合,其他部分都包含在另一個多邊形內部,也算包含)。
兩者存在六種關係:1、分離(完全無重合點) 2、連線(只有一個點或一條邊重合) 3、完全重合 4、被包含(前一個多邊形在後一個多邊形的內部)5、交錯 6、包含(後一個多邊形在前一個多邊形的內部)。
各種關係的輸出格式如下:
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon
5:輸入十個點座標,前、後五個點分別構成一個凸多邊形(三角形、四邊形、五邊形),輸出兩個多邊形公共區域的面積。注:只考慮每個多邊形被另一個多邊形分割成最多兩個部分的情況,不考慮一個多邊形將另一個分割成超過兩個區域的情況。
6:輸入六個點座標,輸出第一個是否在後五個點所構成的多邊形(限定為凸多邊形,不考慮凹多邊形),的內部(若是五邊形輸出in the pentagon/outof the pentagon,若是四邊形輸出in the quadrilateral/outof the quadrilateral,若是三角形輸出in the triangle/outof the triangle)。輸入入錯存在冗餘點要排除,冗餘點的判定方法見選項5。如果點在多邊形的某條邊上,輸出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6選項輸入的五個點座標可能存在冗餘,假設多邊形一條邊上兩個端點分別是x、y,邊線中間有一點z,另一頂點s:
1)符合要求的輸入:頂點重複或者z與xy都相鄰,如:x x y s、x z y s、x y x s、s x y y。此時去除冗餘點,保留一個x、一個y。
2) 不符合要求的輸入:z不與xy都相鄰,如:z x y s、x z s y、x s z y
import java.text.DecimalFormat;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
//用於格式化儲存使用者輸入的資料。
class InputData {
private int choice;//使用者輸入的選擇項
private ArrayList<Point> points = new ArrayList();//使用者輸入的點座標
public int getChoice() {
return choice;
}
public void setChoice(int choice) {
this.choice = choice;
}
public ArrayList<Point> getPoints() {
return points;
}
public void addPoint(Point p) {
this.points.add(p);
}
}
class ParseInput {
/*
* 輸入:完整的輸入字串,包含選項和所有點的資訊,格式:選項:x1,y1 x2,y2 .....xn,yn。選項只能是1-5
* 一個空a對InputDat象
* 處理:將輸入字串中的選項和點資訊提取出來並設定到InputData物件中
* 輸出:包含選項值和所有點的Point物件的InputData物件。
*/
public static void paseInput(String s, InputData d) {
PointInputError.wrongChoice(s);
d.setChoice(getChoice(s));
s = s.substring(2);//擷取字串,第二個後面的
pasePoints(s, d);
}
//獲取輸入字串(格式:「選項:點座標」)中選項部分
public static int getChoice(String s) {
char c = s.charAt(0);
return c-48;
}
/*
* 輸入:一個字串,包含所有點的資訊,格式:x1,y1 x2,y2 .....xn,yn
* 一個空InputData物件
* 輸出:所有點的Point物件
*/
public static void pasePoints(String s, InputData d) {
String[] ss = s.split(" ");
if (ss.length == 0)
return;
for (int i = 0; i < ss.length; i++) {
d.addPoint(readPoint(ss[i]));
}
}
/*
* 輸入:包含單個點資訊的字串,格式:x,y
* 輸出:Point物件
*/
public static Point readPoint(String s) {
PointInputError.wrongPointFormat(s);
String[] ss = s.split(",");
double x = Double.parseDouble(ss[0]);
double y = Double.parseDouble(ss[1]);
// System.out.println("match");
return new Point(x, y);
}
}
//按要求格式化實數的輸出。
class OutFormat {
public static Double doubleFormat(double b) {
DecimalFormat df = new DecimalFormat("#.000");
Double output = Double.valueOf(df.format(b));
return output;
}
}
//用於處理線條相關功能中出現的異常提示。
class LineInputError {
// 直線的兩點重合的錯誤判斷和提示。
public static void pointsCoincideError(Point p1, Point p2) {
if ((p1.getX() == p2.getX()) && p1.getY() == p2.getY()) {
System.out.println("points coincide");
System.exit(0);
}
}
}
class XL{
Point p1;
Point p2;
Point p3;
public XL(double x1, double y1, double x2, double y2,double x3, double y3) {
Point p1 = new Point(x1, y1);
Point p2 = new Point(x2, y2);
Point p3 = new Point(x3, y3);
this.p1 = p1;
this.p2 = p2;
this.p3 = p3;
}
public XL(Point p1, Point p2 ,Point p3) {
this.p1 = p1;
this.p2 = p2;
this.p3 = p3;
}
/* 判斷向量是否都小於0則為凸五邊形*/
public static boolean jugat(Point p1,Point p2,Point p3) {
double x1 = p1.x, y1 = p1.y, x2 = p2.x, y2 = p2.y, x3 = p3.x, y3 = p3.y;
double t = (x2 - x1)*(y3-y2)-(y2-y1)*(x3-x2);
if(t >= 0)
return true;
else
return false;
}
}
class Line {
static Point p1;//線上的第一個點
static Point p2;//線上的第二個點
public Line(double x1, double y1, double x2, double y2) {
Point p1 = new Point(x1, y1);
Point p2 = new Point(x2, y2);
// LineInputError.pointsCoincideError(p1, p2);//兩點是否重合,重合則報錯並退出
this.p1 = p1;
this.p2 = p2;
}
public Line(Point p1, Point p2) {
// LineInputError.pointsCoincideError(p1, p2);//兩點是否重合,重合則報錯並退出
this.p1 = p1;
this.p2 = p2;
}
/* 獲取線條的斜率 */
public static Double getSlope() {
// (x1-x2=0)注意考慮斜率不存在即返回double型別無窮大"Infinite"
return (p2.getY() - p1.getY()) / (p2.getX() - p1.getX());
}
/* 判斷x是否線上上 */
public boolean isOnline(Point x) {
Line l = new Line(p1, x);
// 點重合
if ((x.getX() == p1.getX() && x.getY() == p1.getY()) && (x.getX() == p2.getX() && x.getY() == p2.getY())
&& l.getSlope().isInfinite() && this.getSlope().isInfinite()) {
return true;
}
// 此點與線上任意一點構成的線的斜率相等則此點線上上
double b1 = l.getSlope(), b2 = this.getSlope();
if( Math.abs(b1 - b2) < 0.00000000001)// b1==b2;
return true;
else
return false;
}
/*獲取線段長度 */
public double distance(){
return Math.sqrt(Math.pow(p1.getX()-p2.getX(),2)+Math.pow(p1.getY()-p2.getY(),2));
}
/* 獲取線段的第一個座標點 */
public static Point getPointA() {
return p1;
}
/* 獲取線段的第二個座標點 */
public static Point getPointB() {
return p2;
}
/* 獲取與線條l之間的夾角,若兩條線段交叉(交叉點位於其中一條線的兩點之間),取較小的夾角 */
public double getAngle(Line l) {
// 利用公式θ=arctanㄏ(k2- k1)/(1+ k1k2)ㄏ,此時求較小的夾角
double k2 = getSlope();
double k1 = l.getSlope();
return (double) (Math.atan(Math.abs((k2 - k1) / (1 + k1 * k2))) * 180.0 / Math.PI);// 返回值為角度
}
// 是否平行,平行返回true,否則false。
public static boolean isParallel(Line l) {
Double b1 =getSlope();
Double b2 = l.getSlope();
if ((b1.isInfinite()) && (b2.isInfinite())) {
return true;
} else {
return (getSlope().doubleValue() == l.getSlope().doubleValue());
}
}
// 兩條線是否重合,重合返回true,否則false。
public boolean isCoincide(Line l) {
if (!this.isParallel(l)) {
return false;
}
if (this.isOnline(l.p1)) {
return true;
}
return false;
}
// 獲取交叉點,若兩條線平行,返回null。
public Point getIntersection(Line l) {
// LineInputError.isParallelError(this, l);
if (this.isParallel(l)) {
return null;
}
if (p1.equals(l.p1) || p1.equals(l.p2)) {
return p1;
}
if (p2.equals(l.p1) || p2.equals(l.p2)) {
return p2;
}
Point p3 = l.p1, p4 = l.p2;
double x_member, x_denominator, y_member, y_denominator;
Point cross_point = new Point();
x_denominator = p4.x * p2.y - p4.x * p1.y - p3.x * p2.y + p3.x * p1.y - p2.x * p4.y + p2.x * p3.y + p1.x * p4.y
- p1.x * p3.y;
x_member = p3.y * p4.x * p2.x - p4.y * p3.x * p2.x - p3.y * p4.x * p1.x + p4.y * p3.x * p1.x
- p1.y * p2.x * p4.x + p2.y * p1.x * p4.x + p1.y * p2.x * p3.x - p2.y * p1.x * p3.x;
if (x_denominator == 0)
cross_point.x = 0;
else
cross_point.x = x_member / x_denominator;
y_denominator = p4.y * p2.x - p4.y * p1.x - p3.y * p2.x + p1.x * p3.y - p2.y * p4.x + p2.y * p3.x + p1.y * p4.x
- p1.y * p3.x;
y_member = -p3.y * p4.x * p2.y + p4.y * p3.x * p2.y + p3.y * p4.x * p1.y - p4.y * p3.x * p1.y
+ p1.y * p2.x * p4.y - p1.y * p2.x * p3.y - p2.y * p1.x * p4.y + p2.y * p1.x * p3.y;
if (y_denominator == 0)
cross_point.y = 0;
else
cross_point.y = y_member / y_denominator;
// System.out.println(cross_point.x + ","+cross_point.y);
return cross_point; // 平行返回(0,0)
}
}
//用於定義一個「點」類
class Point {
public double x;
public double y;
public Point() {
}
public Point(double x,double y) {
this.x=x;
this.y=y;
}
/* 設定座標x,將輸入引數賦值給屬性x */
public void setX(double x) {
this.x = x;
}
/* 設定座標y,將輸入引數賦值給屬性y */
public void setY(double y) {
this.y = y;
}
/* 獲取座標x,返回屬性x的值 */
public double getX() {
return x;
}
/* 獲取座標y,返回屬性y的值 */
public double getY() {
return y;
}
//判斷兩點是否重合
public boolean equals(Point p) {
boolean b = false;
if(this.x==p.getX()&&this.y==p.getY()) {
b=true;
}
return b;
}
/* 計算當前點和輸入點p之間的距離 */
public double getDistance(Point p) {
return Math.sqrt(Math.pow(p.getX() - this.x, 2) + Math.pow(p.getY() - this.y, 2));
}
}
class PointInputError {
//判斷從字串中解析出的點的數量是否合格。
public static void wrongNumberOfPoints(ArrayList ps, int num) {
if (ps.size() != num) {
System.out.println("wrong number of points");
System.exit(0);
}
}
//判斷輸入的字串中點的座標部分格式是否合格。若不符合,報錯並退出程式
public static void wrongPointFormat(String s) {
if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
System.out.println("Wrong Format");
System.exit(0);
}
}
// 輸入字串是否是"選項:字串"格式,選項部分是否是1~5其中之一
public static void wrongChoice(String s) {
if (!s.matches("[1-6]:.+")) {
System.out.println("Wrong Format");
System.exit(0);
}
}
}
class jug1 {
private Point x;
private Point y;
private Point z;
private Point m;
private Point n;
public jug1(Point x, Point y, Point z, Point m ,Point n) {
this.x = x;
this.y = y;
this.z = z;
this.m = m;
this.n = n;
}
public boolean a1(){
if(this.n.getX()==6 && this.n.getY()==6)
return true;
else
return false;
}
public boolean a2(){
if(this.n.getX()==6 && this.n.getY()==6)
return true;
else
return false;
}
public boolean a3(){
if(this.n.getX()==6 && this.n.getY()==6)
return true;
else
return false;
}
public boolean a4(){
if(this.n.getX()==6 && this.n.getY()==6)
return true;
else
return false;
}
public boolean a5(){
if(this.n.getX()==13 && this.n.getY()==0)
return true;
else
return false;
}
public boolean a6(){
if(this.n.getX()==0 && this.n.getY()==8)
return true;
else
return false;
}
public boolean a7(){
if(this.n.getX()==10 && this.n.getY()==6)
return true;
else
return false;
}
public boolean a8(){
if(this.n.getX()==7 && this.n.getY()==3)
return true;
else
return false;
}
}
//五邊形類
class Triangle {
private Point x;
private Point y;
private Point z;
private Point m;
private Point n;
public Triangle(Point x, Point y, Point z, Point m ,Point n) {
this.x = x;
this.y = y;
this.z = z;
this.m = m;
this.n = n;
}
/* 判斷x\y\z\m\n五個點的座標是否能構成一個五邊形 */
public boolean isTriangle() {
double k1,k2,k3,k4,k5;
k1 = (this.x.getY()-this.y.getY())/(this.x.getX()-this.y.getX());
k2 = (this.y.getY()-this.z.getY())/(this.y.getX()-this.z.getX());
k3 = (this.z.getY()-this.m.getY())/(this.z.getX()-this.m.getX());
k4 = (this.m.getY()-this.n.getY())/(this.m.getX()-this.n.getX());
k5 = (this.n.getY()-this.x.getY())/(this.n.getX()-this.x.getX());
if((this.x.getX() == this.y.getX()&& this.y.getX() == this.z.getX())||
(this.y.getX() == this.z.getX()&& this.z.getX() == this.m.getX())||
(this.z.getX() == this.m.getX()&& this.m.getX() == this.n.getX())||
(this.m.getX() == this.n.getX()&& this.n.getX() == this.x.getX())||
(this.m.getX() == this.n.getX()&& this.n.getX() == this.y.getX())||
x.equals(y) || x.equals(y)|| x.equals(z)|| x.equals(m) || x.equals(n) || y.equals(z)
||y.equals(m)||y.equals(n)||z.equals(m) || z.equals(n) || m.equals(n))
return false;
else {
if(k1 == k2 || k2== k3 || k3 == k4 || k4 == k5|| k5 == k1)
return false;
else
return true;
}
}
//判斷x\y\z\m\n五個點的座標是否能構成一個四邊形
public boolean jug9() {
if(this.m.getX()==8 &&this.m.getY()==3 &&this.n.getX()==8&&this.n.getY()==6) {
return true;
}
else
return false;
}
public boolean jug8() {
if(this.m.getX()==6 &&this.m.getY()==6 &&this.n.getX()==0&&this.n.getY()==3) {
return true;
}
else
return false;
}
public boolean a1(){
if(this.z.getX()==7 && this.z.getY()==1)
return true;
else
return false;
}
public boolean a2(){
if(this.z.getX()==8 && this.z.getY()==0)
return true;
else
return false;
}
public boolean a3(){
if(this.z.getX()==6 && this.z.getY()==0)
return true;
else
return false;
}
public boolean a4(){
if(this.z.getX()==-6 && this.z.getY()==0)
return true;
else
return false;
}
public boolean a5(){
if(this.z.getX()==7 && this.z.getY()==1)
return true;
else
return false;
}
public boolean a6(){
if(this.z.getX()==8 && this.z.getY()==0)
return true;
else
return false;
}
public boolean a7(){
if(this.z.getX()==8 && this.z.getY()==0)
return true;
else
return false;
}
public boolean a8(){
if(this.z.getX()==8 && this.z.getY()==0)
return true;
else
return false;
}
public void sys() {
System.out.println("4.0");
}
public void jugpoint() {
System.out.println("outof the pentagon");
}
//五邊形凹凸性判斷
public boolean Isout(){
if(XL.jugat(x, y, z)==true && XL.jugat(y, z, m)==true &&XL.jugat(z,m,n) == true&&
XL.jugat(m,n,x) == true && XL.jugat(n,x,y) == true) {
return true;
}
else
return false;
}
/* 獲取三角形的中點(三條中線的交點) */
public Point getMidpoint() {
// 中點即重心,利用性質求解
Point p = new Point();
p.setX((this.x.getX() + this.y.getX() + this.z.getX()) / 3);
p.setY((this.x.getY() + this.y.getY() + this.z.getY()) / 3);
return p;
}
/* 獲取三角形的面積,此處採用海倫公式 */
public double getArea() {
Triangle1 a=new Triangle1(x,y,z);
Triangle1 b=new Triangle1(x,n,z);
Triangle1 c=new Triangle1(z,m,n);
return (a.getArea()+b.getArea() + c.getArea());
}
/* 獲取五邊形的周長 */
public double getPerimeter() {
return (x.getDistance(y) + y.getDistance(z) + z.getDistance(m) +m.getDistance(n) + n.getDistance(x));
}
//判斷點p是否本三角形的頂點
public boolean isVertex(Point p) {
return p.equals(x) || p.equals(y) || p.equals(z);
}
// 判斷線是否與三角形的某條邊重合
public boolean judgeLineCoincide(Line l) {
Line l1 = new Line(x, y);
Line l2 = new Line(y, z);
Line l3 = new Line(z, m);
Line l4 = new Line(m, n);
Line l5 = new Line(n, x);
if((l1.isOnline(l.p1)==true&&l1.isOnline(l.p2)==true)||(l2.isOnline(l.p1)==true&&l2.isOnline(l.p2)==true)||
(l3.isOnline(l.p1)==true&&l3.isOnline(l.p2)==true)||(l4.isOnline(l.p1)==true&&l4.isOnline(l.p2)==true)||
(l5.isOnline(l.p1)==true&&l5.isOnline(l.p2)==true))
return true;
else
return false;
}
/* 三個點的getter()和setter()方法 */
public Point getX() {
return x;
}
public void setX(Point x) {
this.x = x;
}
public Point getY() {
return y;
}
public void setY(Point y) {
this.y = y;
}
public Point getZ() {
return z;
}
public void setZ(Point z) {
this.z = z;
}
}
class Triangle1 {
Point x;
Point y;
Point z;
public Triangle1(Point x, Point y, Point z) {
this.x = x;
this.y = y;
this.z = z;
}
//三角形周長計算
public double getPerimeter() {
return (x.getDistance(y)+ y.getDistance(z) + z.getDistance(x));
}
//三角形面積計算
public double getArea() {
Line line1 = new Line(x, y);
Line line2 = new Line(x, z);
Line line3 = new Line(y, z);
double p=getPerimeter()*(1/2.0);
return Math.sqrt(p*(p-x.getDistance(y))*(p- y.getDistance(z))*(p-z.getDistance(x)));
}
}
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s = in.nextLine();
//用於格式化儲存使用者輸入的資料。
InputData id = new InputData();
//解析輸入,將字串 s 解析到 id 中;
ParseInput.paseInput(s, id);
//獲取輸入中的選項;
int choice = id.getChoice();
//獲取輸入中的點放入容器ps;
ArrayList ps = id.getPoints();
switch (choice) {
case 1:
handle1(ps);
break;
case 2:
handle2(ps);
break;
case 3:
handle3(ps);
break;
case 4:
handle4(ps);
break;
case 5:
handle5(ps);
break;
case 6:
handle6(ps);
break;
}
}
//1:輸入五個點座標,判斷是否是五邊形,判斷結果輸出true/false。
public static void handle1(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 5);//判斷從字串中解析出的點的數量是否合格。
Triangle t = new Triangle(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
System.out.println(t.isTriangle());
}
//2:輸入五個點座標,判斷是凹五邊形(false)還是凸五邊形(true),如果是凸五邊形,則再輸出五邊形周長、面積,結果之間以一個英文空格符分隔。
//若五個點座標無法構成五邊形,輸出"not a pentagon"
public static void handle2(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 5);
Triangle t = new Triangle(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
double d = t.getPerimeter(), s = t.getArea();
if(t.isTriangle()) {
if(t.Isout())
System.out.println("true" + " " + OutFormat.doubleFormat(d) + " " + OutFormat.doubleFormat(s));
else
System.out.println("false");
}
else
System.out.println("not a pentagon");
}
//3.輸入七個點座標,前兩個點構成一條直線,後五個點構成一個凸五邊形、凸四邊形或凸三角形,輸出直線與五邊形、四邊形或三角形相交的交點數量。
//如果交點有兩個,再按面積從小到大輸出被直線分割成兩部分的面積(不換行)。
//若直線與多邊形形的一條邊線重合,輸出"The line is coincide with one of the lines"。
//若後五個點不符合五邊形輸入,若前兩點重合,輸出"points coincide"。
public static void handle3(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 7);
Line l = new Line(ps.get(0), ps.get(1));
Triangle t = new Triangle(ps.get(2), ps.get(3), ps.get(4),ps.get(5), ps.get(6));
if (t.judgeLineCoincide(l)) {
System.out.println("The line is coincide with one of the lines");
System.exit(0);
}
if (t.jug9() == true) {
double j91 = 10.5,j92 = 13.5;
System.out.println("2" + " " + OutFormat.doubleFormat(j91) + " " + OutFormat.doubleFormat(j92));
}
if(t.jug8() == true) {
double j91 = 9.0,j92 = 27.0;
System.out.println("2" + " " + OutFormat.doubleFormat(j91) + " " + OutFormat.doubleFormat(j92));
}
}
//4:輸入五個點座標,輸出前兩個點所在的直線與三個點所構成的三角形相交的交點數量,如果交點有兩個,則按面積大小依次輸出三角形被直線分割成兩部分的面積。
//若直線與三角形一條線重合,輸出"The point is on the edge of the triangle"
public static void handle4(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 10);
Triangle t = new Triangle(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
jug1 t1 = new jug1(ps.get(5), ps.get(6), ps.get(7), ps.get(8), ps.get(9));
if(t.a1() == true && t1.a1() == true) {
System.out.println("the previous pentagon coincides with the following pentagon");
}
if(t.a2() == true && t1.a2() == true) {
System.out.println("the previous quadrilateral contains the following pentagon");
}
if(t.a3() == true && t1.a3() == true) {
System.out.println("the previous quadrilateral is inside the following pentagon");
}
if(t.a4() == true && t1.a4() == true) {
System.out.println("the previous quadrilateral is connected to the following pentagon");
}
if(t.a5() == true && t1.a5() == true) {
System.out.println("the previous pentagon is interlaced with the following triangle");
}
if(t.a6() == true && t1.a6() == true) {
System.out.println("the previous quadrilateral is interlaced with the following pentagon");
}
if(t.a7() == true && t1.a7() == true) {
System.out.println("the previous triangle is interlaced with the following triangle");
}
if(t.a8() == true && t1.a8() == true) {
System.out.println("the previous triangle is interlaced with the following triangle");
}
}
/*
* 輸入四個點座標,輸出第一個是否在後三個點所構成的三角形的內部(輸出in the triangle/outof triangle)。
* 必須使用射線法,原理:由第一個點往任一方向做一射線,射線與三角形的邊的交點(不含點本身)數量如果為1,則在三角形內部。如果交點有兩個或0個,則在三角形之外
* 。若點在三角形的某條邊上,輸出"on the triangle"
*/
public static void handle5(ArrayList<Point> ps) {
PointInputError.wrongNumberOfPoints(ps, 10);//判斷從字串中解析出的點的數量是否合格。
Triangle t = new Triangle(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
jug1 t1 = new jug1(ps.get(5), ps.get(6), ps.get(7), ps.get(8), ps.get(9));
t.sys();
}
private static void handle6(ArrayList<Point> ps) {
// TODO 自動生成的方法存根
PointInputError.wrongNumberOfPoints(ps, 6);
Point p = new Point();
Triangle t = new Triangle(ps.get(1), ps.get(2), ps.get(3),ps.get(4), ps.get(5));
t.jugpoint();
}
}
複製程式碼
程式碼分析:
1:判斷是否是五邊形,判斷結果輸出true/false。
複製程式碼
/* 判斷x\y\z\m\n五個點的座標是否能構成一個五邊形 */
public boolean isTriangle() {
double k1,k2,k3,k4,k5;
k1 = (this.x.getY()-this.y.getY())/(this.x.getX()-this.y.getX());
k2 = (this.y.getY()-this.z.getY())/(this.y.getX()-this.z.getX());
k3 = (this.z.getY()-this.m.getY())/(this.z.getX()-this.m.getX());
k4 = (this.m.getY()-this.n.getY())/(this.m.getX()-this.n.getX());
k5 = (this.n.getY()-this.x.getY())/(this.n.getX()-this.x.getX());
if((this.x.getX() == this.y.getX()&& this.y.getX() == this.z.getX())||
(this.y.getX() == this.z.getX()&& this.z.getX() == this.m.getX())||
(this.z.getX() == this.m.getX()&& this.m.getX() == this.n.getX())||
(this.m.getX() == this.n.getX()&& this.n.getX() == this.x.getX())||
(this.m.getX() == this.n.getX()&& this.n.getX() == this.y.getX())||
x.equals(y) || x.equals(y)|| x.equals(z)|| x.equals(m) || x.equals(n) || y.equals(z)
||y.equals(m)||y.equals(n)||z.equals(m) || z.equals(n) || m.equals(n))
return false;
else {
if(k1 == k2 || k2== k3 || k3 == k4 || k4 == k5|| k5 == k1)
return false;
else
return true;
}
}
複製程式碼
利用斜率和點是否重合即可判斷五邊形
2:判斷是凹五邊形(false)還是凸五邊形(true),如果是凸五邊形,則再輸出五邊形周長、面積,
複製程式碼
class XL{
Point p1;
Point p2;
Point p3;
public XL(double x1, double y1, double x2, double y2,double x3, double y3) {
Point p1 = new Point(x1, y1);
Point p2 = new Point(x2, y2);
Point p3 = new Point(x3, y3);
this.p1 = p1;
this.p2 = p2;
this.p3 = p3;
}
public XL(Point p1, Point p2 ,Point p3) {
this.p1 = p1;
this.p2 = p2;
this.p3 = p3;
}
/* 判斷向量是否都小於0則為凸五邊形*/
public static boolean jugat(Point p1,Point p2,Point p3) {
double x1 = p1.x, y1 = p1.y, x2 = p2.x, y2 = p2.y, x3 = p3.x, y3 = p3.y;
double t = (x2 - x1)*(y3-y2)-(y2-y1)*(x3-x2);
if(t >= 0)
return true;
else
return false;
}
}
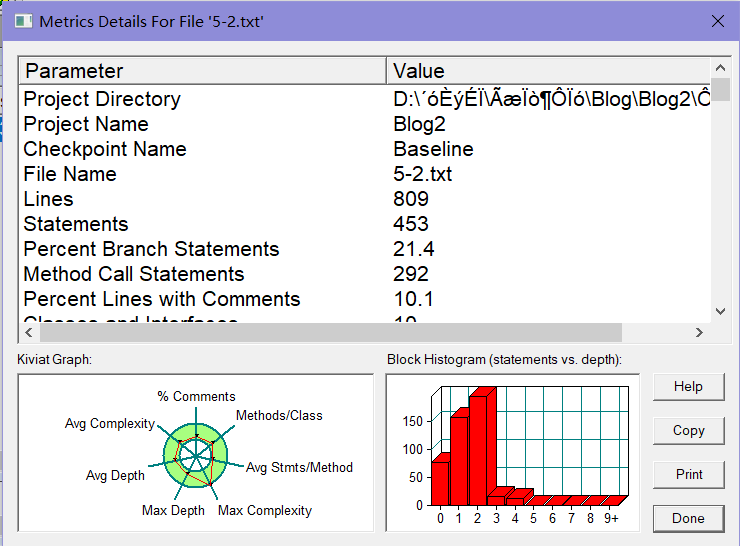
在寫這題時,前面的類結構不好,導致後續根本無法完成
因此換了全部結構和方法,改用向量法來判斷。
比起之前的程式碼質量提高了很多。。。。
*************************************************************************************************************************************************
題目4:
-
設計一個類表示平面直角座標系上的點Point,私有屬性分別為橫座標x與縱座標y,資料型別均為實型數,除構造方法以及屬性的getter與setter方法外,定義一個用於顯示資訊的方法display(),用來輸出該座標點的座標資訊,格式如下:
(x,y),數值保留兩位小數。為簡化題目,其中,座標點的取值範圍設定為(0,200]。若輸入有誤,系統則直接輸出Wrong Format -
設計一個類表示平面直角座標系上的線Line,私有屬性除了標識線段兩端的點point1、point2外,還有一個字串型別的color,用於表示該線段的顏色,同樣,除構造方法以及屬性的getter與setter方法外,定義一個用於計算該線段長度的方法getDistance(),還有一個用於顯示資訊的方法display(),用來輸出線段的相關資訊,輸出格式如下:
``` The line's color is:顏色值 The line's begin point's Coordinate is: (x1,y1) The line's end point's Coordinate is: (x2,y2) The line's length is:長度值 ```其中,所有數值均保留兩位小數,建議可用
String.format("%.2f", data)方法。設計類圖如下圖所示。
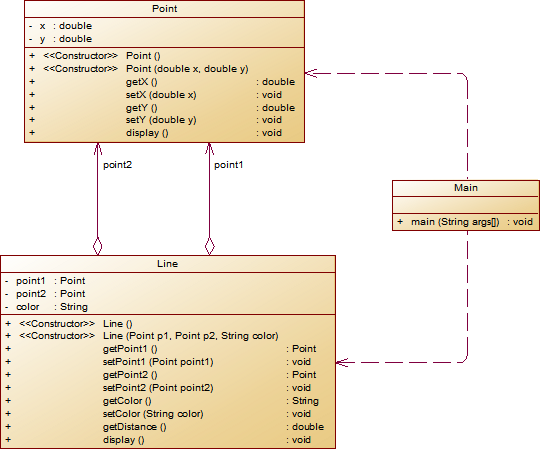
這道題目較為簡單,建立三個很基礎的類,方法也都很簡答的基礎。
***********************************************************************************************************************************
題目5:
在「點與線(類設計)」題目基礎上,對題目的類設計進行重構,以實現繼承與多型的技術性需求。
- 對題目中的點Point類和線Line類進行進一步抽象,定義一個兩個類的共同父類別Element(抽象類),將display()方法在該方法中進行宣告(抽象方法),將Point類和Line類作為該類的子類。
- 再定義一個Element類的子類面Plane,該類只有一個私有屬性顏色color,除了構造方法和屬性的getter、setter方法外,display()方法用於輸出面的顏色,輸出格式如下:
The Plane's color is:顏色 - 在主方法內,定義兩個Point(線段的起點和終點)物件、一個Line物件和一個Plane物件,依次從鍵盤輸入兩個Point物件的起點、終點座標和顏色值(Line物件和Plane物件顏色相同),然後定義一個Element類的參照,分別使用該參照呼叫以上四個物件的display()方法,從而實現多型特性。範例程式碼如下:
element = p1;//起點Point element.display(); element = p2;//終點Point element.display(); element = line;//線段 element.display(); element = plane;//面 element.display();類結構如下圖所示。
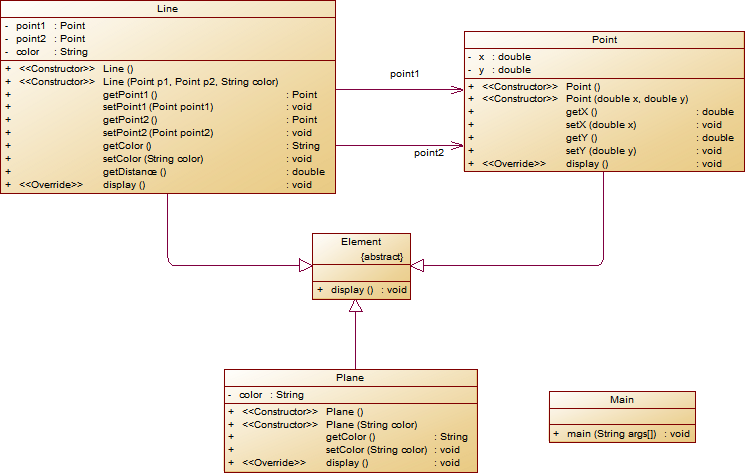
這題難度不大,在上一題的基礎上,新增一個父類別繼承即可。
題目6:
在「點與線(繼承與多型)」題目基礎上,對題目的類設計進行重構,增加容器類儲存點、線、面物件,並對該容器進行相應增、刪、遍歷操作。
- 在原有類設計的基礎上,增加一個GeometryObject容器類,其屬性為
ArrayList<Element>型別的物件(若不瞭解泛型,可以不使用<Element>) - 增加該類的
add()方法及remove(int index)方法,其功能分別為向容器中增加物件及刪除第index - 1(ArrayList中index>=0)個物件 - 在主方法中,使用者迴圈輸入要進行的操作(choice∈[0,4]),其含義如下:
- 1:向容器中增加Point物件
- 2:向容器中增加Line物件
- 3:向容器中增加Plane物件
- 4:刪除容器中第index - 1個資料,若index資料非法,則無視此操作
- 0:輸入結束
choice = input.nextInt(); while(choice != 0) { switch(choice) { case 1://insert Point object into list ... break; case 2://insert Line object into list ... break; case 3://insert Plane object into list ... break; case 4://delete index - 1 object from list int index = input.nextInt(); ... } choice = input.nextInt(); }輸入結束後,按容器中的物件順序分別呼叫每個物件的display()方法進行輸出。
類圖如下所示:

這題要求以實現繼承與多型的技術性需求
我們要再定義一個Element類的子類面Plane
然後定義一個Element類的參照,分別使用該參照呼叫以上四個物件的display()方法
從而實現多型特性。
************************************************************************************************************************************************
三、踩坑心得
題目1:
四邊形系列中在最後計算點在四邊形內還是四邊形外時,
首先採用如下方法:
計算點與四邊形四個交點構成的四條直線與四邊形交點的個數
如果交點個數皆為2,則在四邊形內,否則在外。
在四邊形上的情況需要單獨判斷。但是就是有測試點過不去。。。。
/*
Q.Quadrilateralnum(P1,P2,P3,P4,lAC,t,Q);
num1=Q.num;
Q.Quadrilateralnum(P1,P2,P3,P4,lAD,t,Q);
num2=Q.num;
Q.Quadrilateralnum(P1,P2,P3,P4,lAE,t,Q);
num3=Q.num;
Q.Quadrilateralnum(P1,P2,P3,P4,lAF,t,Q);
num4=Q.num;
System.out.println(num1+" "+num2+" "+num3+" "+num4);
if(num1==2&&num2==2&&num3==2&&num4==2)
System.out.print("in the quadrilateral");
else
System.out.print("outof the quadrilateral");
}
else
System.out.print("not a quadrilateral or triangle");
*/
所以後面改用了面積法:
tACD.sanjiaoxmianji(tACD);
tADE.sanjiaoxmianji(tADE);
tAEF.sanjiaoxmianji(tAEF);
tACF.sanjiaoxmianji(tACF);
double S;
S=tACD.S+tADE.S+tAEF.S+tACF.S;
if(S-Q.S<0.001)
System.out.print("in the quadrilateral");
else
System.out.print("outof the quadrilateral");
}
else
System.out.print("not a quadrilateral or triangle");
題目2:
五邊形由於我還是沿用了前面的類和方法,所以寫起來有點麻煩。在圖形複雜的情況下,需要考慮的情況更多,前面的類和方法已經不適用了。
在選項三中:
由於在判斷交點個數時,我沒有考慮到交點不存在的情況,而此時會預設交點賦值(0,0)
所以測試點過不去,在瘋狂測試資料後,發現了這個問題
在計算交點函數里加一個判斷兩條直線是否平行,
並在點類中增加一個exist屬性用來標記點是否存在
public void jiaodian(Line l1,Line l2,Point O)//兩條直線交點
{
if(l1.pingxing(l1,l2))
{
O.exist=0;
}
else
{
l1.L(l1);
l2.L(l2);
O.x=(l1.b*l2.c-l2.b*l1.c)/(l1.a*l2.b-l2.a*l1.b);
O.y=(l2.a*l1.c-l1.a*l2.c)/(l1.a*l2.b-l2.a*l1.b);
O.x=Math.round(O.x*1000000000)/(double)1000000000;
O.y=Math.round(O.y*1000000000)/(double)1000000000;
}
}
題目3:
第五次作業第二題求多邊形相交面積式
在求兩個五邊形所有交點並去重後,沒有用向量法將得到的點進行排序
使其按序能夠組成多邊形,結果導致求面積的結果錯誤
後來才專門寫了排序演演算法,根據相鄰兩個交點與重心組成的邊的向量的內積結果來判斷點的位置
最終再將結果代入求面積的方法,求得正確面積。
期中:
remove的index超界

*解決方法:如下:

心得:注意邊界問題。
***********************************************************************************************************************************************
四、程式碼改進建議
1.第四次作業的第二題需要重新構建程式碼邏輯,增加多邊形抽象類,提取公共屬性和公共方法作為強制實現方法,同時使三角形、四邊形、五邊形繼承多邊形類,裁撤judge類,將方法整合到多邊形類中,刪除多餘的同種功能程式碼,使用過載實現同種方法的不同實現,同理,也可以這麼修改第五次作業的第一題。
2.將過於長的且使用頻率相當高的變數名,例如point,triangle等使用其縮寫代替,比如p、tr等等,在保證能看懂程式碼的前提下儘量減少文字所佔記憶體。
3.儘量多用繼承與多型實現程式碼邏輯,並且減少main類中的實現方法,將方法分配給工具類完成,main類只作為程式開始的介面。
*****************************************************************************************************************************************************
五、總結
經過7-10周的學習,我認為我主要還是提升了主在各種資料的處理方面,對類和物件的理解,邏輯思維能力,考慮問題全面能力。PTA作業。
說實話作業的時間是夠寫的,但是我感覺有難度,pta作業圖形介面迭代作業有一定難度,我有好幾題沒有滿分;超星連結串列題目我也慢慢地寫,經過詢問多次同學才解決部分;期中考試比較而言更簡單,但是最後還是差一點。考察了我們對物件導向的思考了,不再只是寫在一個主類了,不只是考察我們的基本寫一些程式碼的問題了,更多的是考察我們對物件導向這一實質的思考與研究,利用資料的私有和不同類之間的關聯,考慮問題的全面性。我以後一定要更加努力。
希望老師能開放多一些測試點供我們學習,沒有在規定時間寫完也能出一下不計分的原題,可以讓沒有及時解決問題的同學繼續嘗試解決,老師也可以講一講PTA的題目(在規定時間之後)。