機器人到達指定位置的方法數問題

作者：Grey

原文地址：

題目描述

連結：https://www.nowcoder.com/questionTerminal/54679e44604f44d48d1bcadb1fe6eb61
來源：牛客網

假設有排成一行的N個位置，記為1~N，開始時機器人在M位置，機器人可以往左或者往右走，如果機器人在1位置，那麼下一步機器人只能走到2位置，如果機器人在N位置，那麼下一步機器人只能走到N-1位置。規定機器人只能走k步，最終能來到P位置的方法有多少種。由於方案數可能比較大，所以答案需要對1e9+7取模。

暴力解

定義遞迴函數

long ways(int len, int start, int step, int end)

遞迴含義表示：機器人從座標 start 開始，只能走 step 步，到達 end 的方法數是多少。

接下來是 base case，

if (step == 0) {
    if (start == end) {
        return 1L;
    }
    return 0L;
}

如果 step 只剩下 0 步，說明沒有步數可以走了，此時，如果 start == end ，表示正好就在目的地，返回一種方法數；

否則，返回 0 種方法數。

接下來是普遍情況，如果 start == 0，只能向右邊走，即: ways(len, start + 1, step - 1, end)；

如果 start == len - 1，只能向左邊走，即：ways(len, start - 1, step - 1, end)；

不在兩端位置，則既可以向左邊走，也可以向右邊走，即：(ways(len, start - 1, step - 1, end) + ways(len, start + 1, step - 1, end))。

暴力解法完整程式碼如下

    public static long ways(int len, int start, int step, int end) {
        if (step == 0) {
            if (start == end) {
                return 1L;
            }
            return 0L;
        }
        // step不止一步
        if (start == 0) {
            return ways(len, start + 1, step - 1, end);
        } else if (start == len - 1) {
            return ways(len, start - 1, step - 1, end);
        } else {
            return (ways(len, start - 1, step - 1, end) + ways(len, start + 1, step - 1, end));
        }
    }

超時

動態規劃-快取法（可 AC）

上述暴力遞迴過程，可變引數有兩個 start，step；可以設定一個二維陣列 dp，用於快取遞迴中間過程的解，

long[][] dp = new long[len][step + 1];

dp[i][j]表示ways(len,i,j,end)的值，dp陣列的值均初始化為 -1。

上述暴力遞迴過程增加這個 dp 引數，如果dp[i][j] != -1，則說明已經算過這個遞迴過程，直接返回dp[i][j]的值即可。

完整程式碼如下

    public static long ways(int len, int start, int step, int end) {
        long[][] dp = new long[len][step + 1];
        for (int i = 0; i < len; i++) {
            for (int j = 0; j <= step; j++) {
                dp[i][j] = -1L;
            }
        }
        dp(len, start, step, end, dp);
        return dp[start][step];
    }

    private static long dp(int len, int start, int step, int end, long[][] dp) {
        if (dp[start][step] != -1L) {
            return dp[start][step] % MOD;
        }
        if (step == 0) {
            dp[start][step] = start == end ? 1L : 0L;
            return dp[start][step];
        }
        long ans;
        // step不止一步
        if (start == 0) {
            ans = dp(len, start + 1, step - 1, end, dp);
        } else if (start == len - 1) {
            ans = dp(len, start - 1, step - 1, end, dp);
        } else {
            ans = (dp(len, start - 1, step - 1, end, dp) + dp(len, start + 1, step - 1, end, dp));
        }
        dp[start][step] = ans;
        return ans;
    }

動態規劃解-嚴格位置依賴（可 AC）

回到暴力遞迴解，虛擬碼如下

    public static long ways(int len, int start, int step, int end) {
        ……
        if (start == 0) {
            return ways(len, start + 1, step - 1, end);
        } else if (start == len - 1) {
            return ways(len, start - 1, step - 1, end);
        } else {
            return (ways(len, start - 1, step - 1, end) + ways(len, start + 1, step - 1, end));
        }
    }

根據快取法得知，該遞迴過程使用一個二維陣列 dp 即可存下所有結果，其中

dp[i][j]表示ways(len,i,j,end)的值，

通過觀察上述暴力遞迴過程，dp[i][j]依賴的位置是dp[i+1][j-1]，dp[i-1][j-1]，

所以，依據上述遞迴過程，可以改成嚴格位置的動態規劃版本，完整程式碼如下

    public static long ways(int len, int start, int step, int end) {
        long[][] dp = new long[len][step + 1];
        // 填好第0列
        dp[end][0] = 1L;
        for (int j = 1; j < step + 1; j++) {
            for (int i = 0; i < len; i++) {
                if (i == 0) {
                    dp[i][j] = dp[1][j - 1];
                } else if (i == len - 1) {
                    dp[i][j] = dp[len - 2][j - 1];
                } else {
                    dp[i][j] = dp[i - 1][j - 1] % MOD + dp[i + 1][j - 1] % MOD;
                }
            }
        }
        return dp[start][step];
    }

動態規劃解-空間壓縮版（可 AC）

通過上述嚴格位置的動態規劃版本可以得知，dp[i][j]位置，依賴的位置是dp[i+1][j-1]，dp[i-1][j-1],

範例圖如下

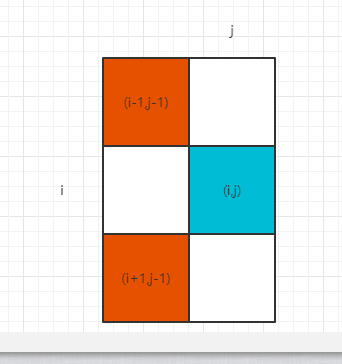
而且，通過上述動態規劃解，可以得知第 0 列中，除了dp[end][0] = 1L，其餘都是 0，所以 dp 的第0列可以直接填充

所以，只需要用一個一維陣列表示第 0 列，然後根據依賴關係，通過第 0 列推出第一列的值，一維陣列此時表示第一列的值，依次這樣遞推下去，一直到最後一列，得解，這種方法就可以將二維陣列壓縮成一維陣列，節省了空間複雜度。

完整程式碼如下

    public static long ways(int len, int start, int step, int end) {
        long[] dp = new long[len];
        dp[end] = 1L;
        long tmp = 0;
        for (int j = 1; j < step + 1; j++) {
            for (int i = 0; i < len; i++) {
                long ways = dp[i];
                if (i == 0) {
                    dp[i] = dp[1] % MOD;
                } else if (i == len - 1) {
                    dp[i] = tmp % MOD;
                } else {
                    dp[i] = tmp % MOD + dp[i + 1] % MOD;
                }
                tmp = ways;
            }
        }
        return dp[start];
    }

演演算法和資料結構筆記

機器人到達指定位置的方法數問題

機器人到達指定位置的方法數問題

題目描述

暴力解

動態規劃-快取法（可 AC）

動態規劃解-嚴格位置依賴（可 AC）

動態規劃解-空間壓縮版（可 AC）

更多