1 導引

我們在部落格《聯邦學習：聯邦場景下的多源知識圖譜嵌入》中介紹了聯邦場景下的知識圖譜嵌入，現在讓我們回顧一下其中關於資料部分的細節。在聯邦場景下，\(C\)個知識圖譜\(\left\{\mathcal{G}_c\right\}_{c=1}^C=\left\{\left\{\mathcal{E}_c, \mathcal{R}_c, \mathcal{T}_c\right\}\right\}_{c=1}^C\)位於不同的使用者端上。知識圖譜擁的實體集合\(\mathcal{E}_c\)之間可能會存在重疊，而其關係集合\(\mathcal{R}_c\)和元組集合\(\mathcal{T}_c\)之間則不會重疊^[1]。我們聯絡一下現實場景看這是合理的，比如在不同使用者端對應不同銀行的情況下，由於不同銀行都有著自己的業務流程，所以關係集合不重疊。

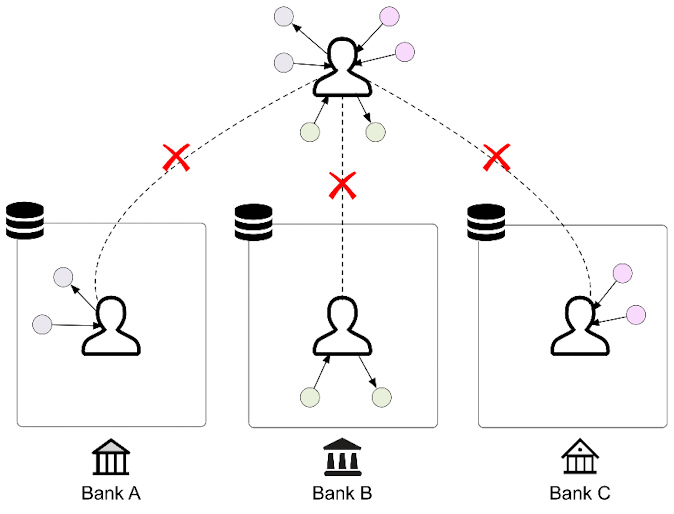
接下來我們來看具體在實驗環節怎麼去劃分聯邦異構知識圖譜資料。

2 聯邦異構知識圖譜劃分

我們在部落格《分散式機器學習：PageRank演演算法的並行化實現（PySpark）》中所說，分散式圖資料的劃分可分為點劃分和邊劃分兩種，邊劃分是對圖中某些邊進行分裂，這使得不同的worker的點不同，但可能存有相同的邊拷貝。而點劃分是對圖中某些點進行分裂，使得不同的worker的邊不同，可能存有相同的點拷貝。不過知識圖譜的情況要簡化得多，因為知識圖譜的圖資料本身就是按一條條的邊(元組)\((h,r,t)\)來儲存的，直接對元組進行劃分其實就等價於了點劃分的方式。

由於我們這裡的本地知識圖譜\(\{\mathcal{E}_c, \mathcal{R}_c, \mathcal{T}_c\}\)中每個知識圖譜的關係\(\mathcal{R}_c\)（即邊的種類）是不同的，我們在劃分元組之前我們需要先對關係進行劃分，然後針對關係劃分的結果來劃分元組。待元組劃分到本地後，還需要將原有的實體和關係的索引對映到本地索引。最後，再在本地進行訓練/驗證/測試集的拆分。整體資料劃分流程圖如下：

2.1 劃分關係

我們選擇隨機地將關係\(\mathcal{R}\)不重疊地劃分到不同的client上：

random.shuffle(triples)
# triples為元祖集合，大小為 (n_triples, 3)
# 每各元組按(h,t,r)順序儲存
triples = np.concatenate(triples) 

# 先根據邊的型別edge_type（即關係型別)將不同的edge_type對映到不同的client_id
edge_types = list(set(triples[:, 2]))
random.shuffle(edge_types)
edge_type_to_cid = {}
n_edge_types_per_client = len(edge_types)//n_clients
for id, edge_type in enumerate(edge_types):
    c_id = id // n_edge_types_per_client
    if c_id < n_clients - 1:
        edge_type_to_cid[edge_type] = c_id
    else:
        edge_type_to_cid[edge_type] = n_clients - 1

2.2 確定元組劃分

在關係的劃分確定之後，我們可以根據每個元組\((h,r,t)\)中\(r\)的劃分情況來決定該元組的劃分情況。程式碼如下：

# 然後根據edge_type到client_id的對映情況，來將元組triples劃分到不同的client
c_id_triples = [[] for i in range(n_clients)]    
for triple in triples:
    edge_type = triple[2]
    c_id = edge_type_to_cid[edge_type]
    c_id_triples[c_id].append(triple.reshape(1, -1))

2.3 索引對映

劃分好元組之後，子圖就確定了，接下來我們還需要將子圖的實體和關係的索引進行重新編號，如下圖所示：

對於具體的區域性索引如何安排，我們採用隨機選擇的方式。程式碼如下：

# mapping global indices to local indices
c_id_triples_ori = [[] for i in range(n_clients)]    
for c_id in range(n_clients):
    triples = np.concatenate(c_id_triples[c_id])
    c_id_triples_ori[c_id] = triples
            
    edge_index = triples[:, :2]
    edge_type = triples[:, 2]

    # map entity indices to local entity indices
    index_mapping = {}
    entities = list(set(edge_index.flatten()))
    random.shuffle(entities)
    for index, entity in enumerate(entities):
        index_mapping[entity] = index
    f = lambda x: index_mapping[x]
    f = np.vectorize(f)
    client_entity_local_index = f(edge_index)

    # map edge indices to local entity indices
    index_mapping = {}
    edges = copy.deepcopy(list(set((edge_type))))
    random.shuffle(edges)
    for index, edge in enumerate(edges):
        index_mapping[edge] = index
    f = lambda x: index_mapping[x]
    f = np.vectorize(f)
    client_edge_local_index = f(edge_type)

    c_id_triples[c_id] = np.concatenate([client_entity_local_index, \
        client_edge_local_index.reshape(-1, 1)], axis=1)

2.4 訓練/驗證/測試集拆分

最後，還需要在本地劃分訓練集、驗證集和測試集。如下面的程式碼展示了按照0.8/0.1/0.1對原生的元組進行拆分。資料集劃分完畢之後，則訓練/驗證/測試集對應的實體(edge_index)和關係型別(edge_type)就都確立了：

# split train, valid, test dataset
for c_id in range(n_clients):
    n_triples = c_id_triples[c_id].shape[0]
    n_train = int(n_triples * 0.8)
    n_val = int((n_triples - n_train) * 0.5)
    n_test = n_triples - n_train - n_val

    mod_to_slice = {"train": slice(0, n_train), \
        "valid": slice(n_train, n_train+n_val), "test": slice(-n_test, n_triples)}
    for mode in ["train", "valid", "test"]:
        client_data[c_id][mode]["edge_index_ori"] = c_id_triples_ori[c_id][mod_to_slice[mode], : 2].T
        client_data[c_id][mode]["edge_index"] = c_id_triples[c_id][mod_to_slice[mode], : 2].T
        
        client_data[c_id][mode]["edge_type_ori"] = c_id_triples_ori[c_id][mod_to_slice[mode], 2]
        client_data[c_id][mode]["edge_type"] = c_id_triples[c_id][mod_to_slice[mode], 2]

3 關於異構性的分析和解決

根據我們前面的定義，在聯邦場景下不同使用者端的知識圖譜滿足實體重疊，因此在進行聯邦訓練的過程中最簡單的方式就是對重疊實體的embeddings進行平均。但是我們知道，知識圖譜可能本身就具有一定的異構性，因為其中的某個實體可能會擁有著不同的關係路徑^[2]，如下圖所示：

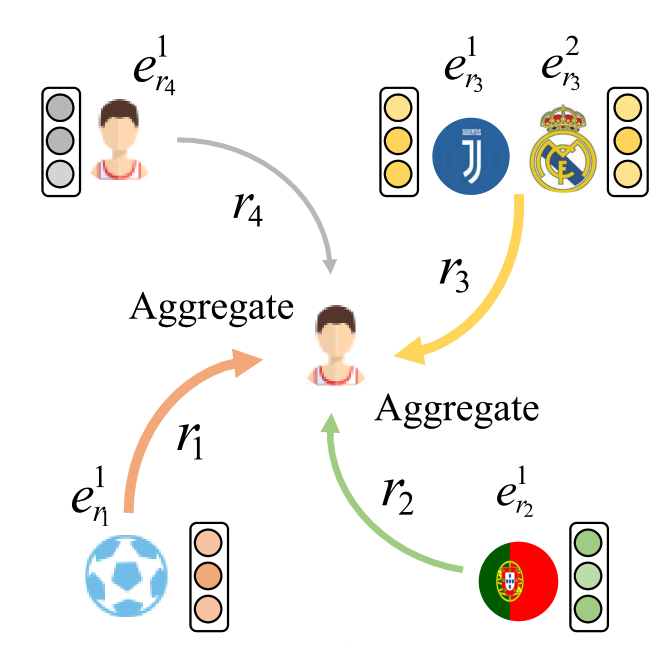
在聯邦場景下這種異構性則更加明顯，因為如我們前面所說，同一個實體在不同的client的關係路徑肯定不同，如果只採用本地嵌入的方法，那麼不同的client會對映到不同的嵌入空間。此時，如果對來自不同嵌入空間embeddings直接進行聚合，就會丟失掉許多有用的語意資訊。

如上圖所示^[3]，知識圖譜School中的元組表示Bob和Jack的學業資訊，Amazon.com知識圖譜中則表示他們的購物資訊。對於Bob和Jack實體而言，在不同的知識圖譜中他們擁有不同的關係，導致了他們的語意資訊在不同知識圖譜中的差異。

如何對聯邦場景下知識圖譜的異構性進行解決，成為一個必須要考慮的問題，目前文獻^[3]已採用對比學習對其進行了一定程度的解決，大家感興趣的可以去閱讀一下。

參考

[1] Chen M, Zhang W, Yuan Z, et al. Fede: Embedding knowledge graphs in federated setting[C]//The 10th International Joint Conference on Knowledge Graphs. 2021: 80-88.
[2] Li Z, Liu H, Zhang Z, et al. Learning knowledge graph embedding with heterogeneous relation attention networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021.
[3] Chen M, Zhang W, Yuan Z, et al. Federated knowledge graph completion via embedding-contrastive learning[J]. Knowledge-Based Systems, 2022, 252: 109459.

聯邦學習：聯邦異構知識圖譜資料劃分