演演算法 | 詳解斐波那契數列問題

本篇是學習了《趣學演演算法（第2版）》第一章之後總結的。

上一篇講到了等比數列求和問題，求$S_n = 1 + 2 + 2^2 + 2^3 + ... + 2^{63}= ？$，該函數屬於爆炸增量函數，如果採用常規運算，則要考慮演演算法的時間複雜度。

演演算法知識點

斐波那契數
動態規劃（拆分子問題；記住過往，減少重複計算）

演演算法題目

假設第1個月有1對初生的兔子，第2個月進入成熟期，第3個月開始生育兔子，而1對成熟的兔子每月會生
1對兔子，兔子永不死去..…那麼，由1對初生的兔子開始，12個月後會有多少對兔子呢？

做題思路

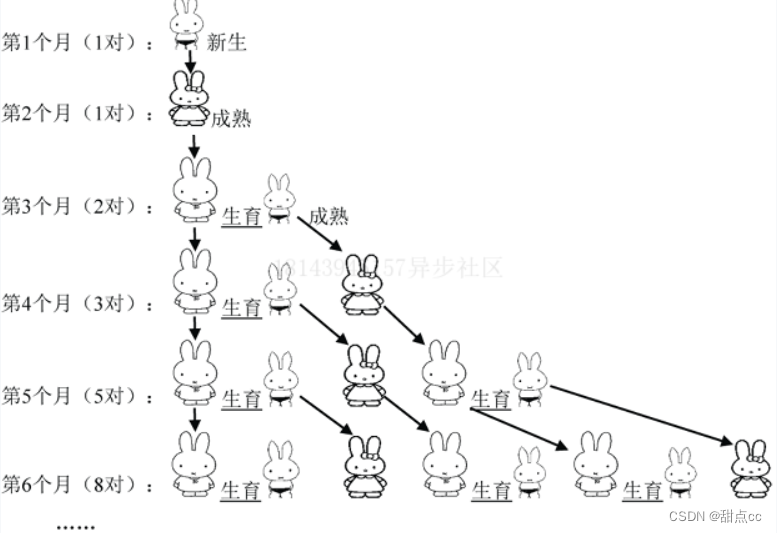
這個數列有如下十分明顯的特點：從第3個月開始，$當月的兔子數=上月兔子數+當月新生兔子數$，而$當月新生兔子數=上上月的兔子數$。因此，前面相鄰兩項之和便構成後一項，換言之：
$$當月的兔子數=上月兔子數+上上月的兔子數$$

斐波那契數如下：

1 ，1 ，2 ，3 ，5 ，8， 13 ，21 ，34 ......

遞迴表示式

$$F(n)=
\begin{cases}
1&， \text{n=1}\
1&， \text{n=2}\
F(n-1) + F(n-2)&， \text{n>2}
\end{cases}$$

根據遞迴表示式，初步的演演算法程式碼如下：

const fbn = (n) => {
  if (n == 1 || n == 2) {
		return 1
  } else {
		return fbn(n-2) + fbn(n-1)
	}
}

讓我們看一下上面演演算法的時間複雜度，也就是計算的總次數$T(n)$

時間複雜度

時間複雜度算的是最壞情況下的時間複雜度

n=1時，T(n)=1
n=2時，T(n)=1；
n=3時，T(n)=3; //呼叫Fib1(2)和Fib1(1)並執行一次加法運算(Fib1(2)+Fib1(1))

當n>2時需要分別呼叫fbn(n-1)和fbn(n-2)，並執行一次加法運算，換言之：
$$n\gt2時，T(n)=T(n-1)+T(n-2)+1;$$

所以，$T(n) >= F(n)$

問題來了，怎麼判斷T(n)屬於演演算法時間複雜度的哪種型別呢？

方法一：

畫出遞迴樹，每個節點表示計算一次

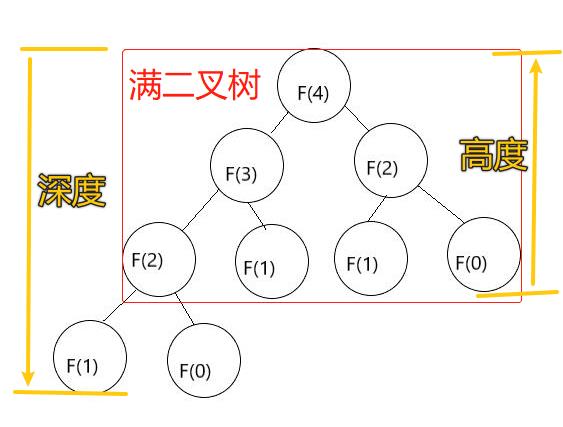
一棵滿二元樹，節點總數就和樹的高度呈指數關係

遞迴樹 F(n)裡面存在滿二元樹，所以時間複雜度是指數階的。

方法二：

使用公式進行遞推

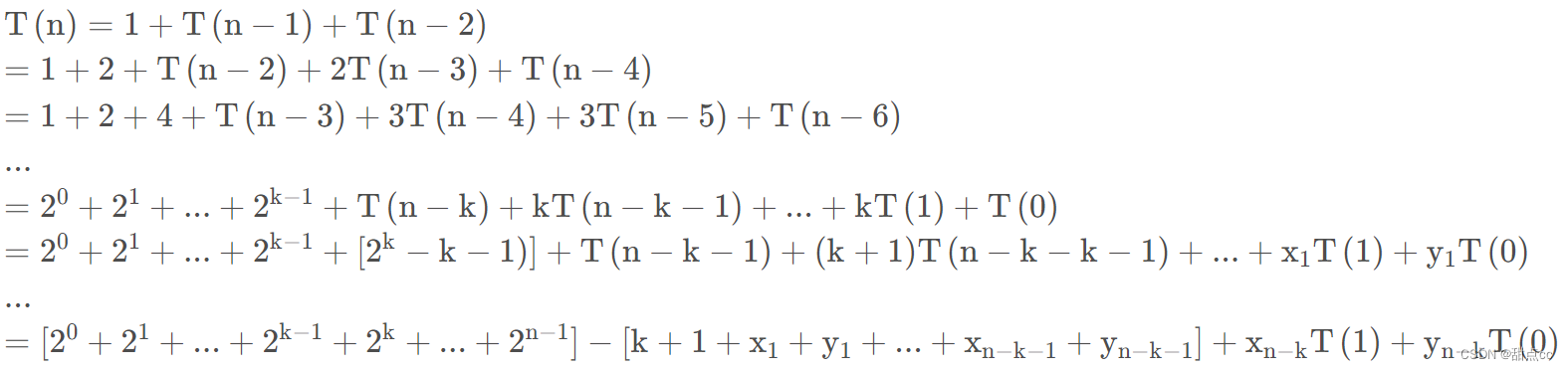
因為時間複雜度算的是最壞情況下的時間複雜度，所以計算第一個括號內的即可

即：$T(n) = O(2^n)$，時間複雜度是指數階的

演演算法改進

降低時間複雜度

不難發現：上面基於遞迴表示式的演演算法，存在大量的重複計算，增大了演演算法的時間複雜度，所以我們可以做出如下改進，以減少時間複雜度

// 利用陣列記錄過往的值，直接使用，避免重複計算
const fbn2 = (n) => {
  let arr = new Array(n + 1); // 定義 n + 1 長度的陣列
  arr[1] = 1;
  arr[2] = 1;
  for (let i = 3; i <= n; i++) {
    arr[i] = arr[i - 1] + arr[i - 2]
  }
  return arr[n]
}

很顯然上面演演算法的時間複雜度是$O(n)$，時間複雜度從指數階降到了多項式階。

由於上面演演算法使用陣列記錄了所有項的值，所以，演演算法的空間複雜度變成了$O(n)$，我們可以繼續改進演演算法，來降低演演算法的空間複雜度

降低空間複雜度

採用臨時變數，來迭代記錄上一步計算出來的值，程式碼如下：

const fbn3 = (n) => {
  if (n === 1 || n === 2) {
    return 1;
  }
  let pre1 = 1 // pre1，pre2記錄前面兩項
  let pre2 = 1
  let tmp = ''

  for (let i = 3; i <= n; i++) {
    tmp = pre1 + pre2 // 2
    pre1 = pre2 // 1
    pre2 = tmp // 2
  }
  return pre2
}

使用了三個輔助變數，時間複雜度還是$O(n)$，空間複雜度降為$O(1)$

測試演演算法計算時間

// 斐波那契數列
// 1 ，1 ，2 ，3 ，5 ，8， 13 ，21 ，34 ......

const fbn = (n) => {
  if (n == 1 || n == 2) {
		return 1
  } else {
		return fbn(n-2) + fbn(n-1)
	}
}
console.time('fbn')
console.log('fbn(40)=', fbn(40))
console.timeEnd('fbn')

// 利用陣列記錄過往的值，直接使用，避免重複計算
const fbn2 = (n) => {
  let arr = new Array(n + 1); // 定義 n + 1 長度的陣列
  arr[1] = 1;
  arr[2] = 1;
  for (let i = 3; i <= n; i++) {
    arr[i] = arr[i - 1] + arr[i - 2]
  }
  return arr[n]
}

console.time('fbn2')
console.log('fbn2(40)=', fbn2(40))
console.timeEnd('fbn2')

const fbn3 = (n) => {
  if (n === 1 || n === 2) {
    return 1;
  }
  let pre1 = 1 // pre1，pre2記錄前面兩項
  let pre2 = 1
  let tmp = ''

  for (let i = 3; i <= n; i++) {
    tmp = pre1 + pre2 // 2
    pre1 = pre2 // 1
    pre2 = tmp // 2
  }
  return pre2
}

console.time('fbn3')
console.log('fbn3(40)=', fbn3(40))
console.timeEnd('fbn3')

測試結果如下：

fbn(40)= 102334155
fbn: 667.76ms
fbn2(40)= 102334155
fbn2: 0.105ms
fbn3(40)= 102334155
fbn3: 0.072ms

小結

能不能繼續降階，使演演算法的時間複雜度更低呢？
實質上，斐波那契數列的時間複雜度還可以降到對數階$O(logn)$，好厲害!!!後面繼續探索吧

演演算法作為一門學問，有兩條几乎平行的線索：

資料結構（資料物件）：數、矩陣、集合、串、排列、圖、表示式、分佈等。
演演算法策略：貪心策略、分治策略、動態規劃策略、線性規劃策略、搜尋策略等。

這兩條線索是相互獨立的：

對於同一個資料物件上不同的問題（如單源最短路徑和多源最短路徑)，就會用到不同的演演算法策略（如貪心策略和動態規劃策略）；
對於完全不同的資料物件上的問題(如排序和整數乘法)，也許就會用到相同的演演算法策略（如分治策略）。

我是 甜點cc

熱愛前端，也喜歡專研各種跟本職工作關係不大的技術，技術、產品興趣廣泛且濃厚，等待著一個創業機會。本號主要致力於分享個人經驗總結，希望可以給一小部分人一些微小幫助。

希望能和大家一起努力營造一個良好的學習氛圍，為了個人和家庭、為了我國的網際網路物聯網技術、數位化轉型、數位經濟發展做一點點貢獻。數風流人物還看中國、看今朝、看你我。