論文資訊

論文標題：Label-invariant Augmentation for Semi-Supervised Graph Classification
論文作者：Han Yue, Chunhui Zhang, Chuxu Zhang, Hongfu Liu
論文來源：2022，NeurIPS
論文地址：download
論文程式碼：download

1 Introduction

　　我們提出了一種圖對比學習的標籤不變增強策略，該策略涉及到下游任務中的標籤來指導對比增強。值得注意的是，我們不生成任何圖形資料。相反，我們在訓練階段直接生成標籤一致的表示作為增廣圖。

2 Methodology

2.1 Motivation

　　資料增強在神經網路訓練中起著重要的作用。它不僅提高了學習表示的魯棒性，而且為訓練提供了豐富的資料。

　　例子：（使用 $50%$ 的標籤做監督資訊。資料增強：node dropping, edge perturbation, attribute masking, subgraph sampling）

　　顯然有些資料增強策略（或組合）對於模型訓練又負面影響。本文進一步使用 MUTAG 中的 $100%$ 標籤訓練模型，然後以每種資料增強抽樣概率 $0.2$ 選擇資料增強圖，發現 80% 的資料增強圖和原始圖示籤一致，約 $20%$ 的資料增強圖和原始圖示籤不一致。

2.2 Label-invariant Augmentation

　　整體框架：

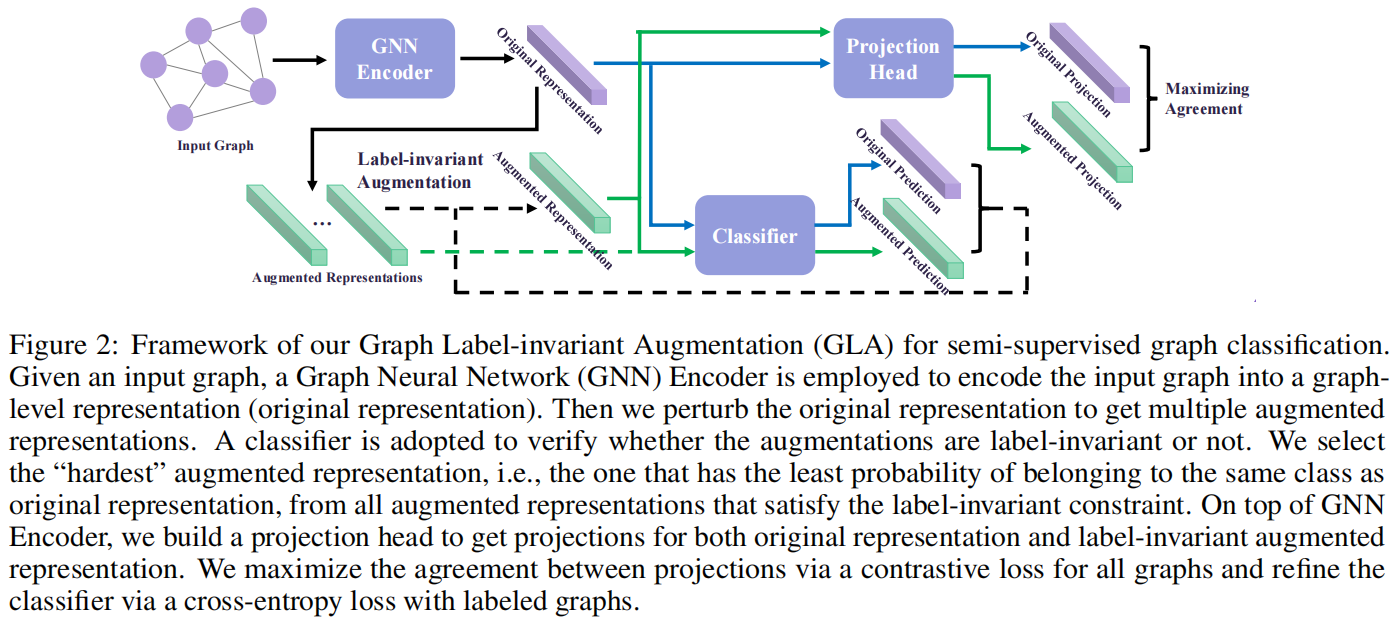
　　四個組成部分：

- Graph Neural Network Encoder
- Classifier
- Label-invariant Augmentation
- Projection Head

　　出發點：對於一個有標記的圖，我們期望由增強表示預測的標籤與地面真實標籤相同。

2.2.1 Graph Neural Network Encoder

　　GCN layer :

　　　　$G^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} G^{(l)} \theta_{G}^{(l)}\right)\quad\quad\quad\quad(1)$

　　其中：

- $G^{(l)}$ denotes the matrix in the l -th layer, and $G^{(0)}=X$
- $\sigma(\cdot)=\operatorname{ReLU}(\cdot)$

　　池化 (sum)：

　　　　$H=\operatorname{Pooling}(G)\quad\quad\quad\quad(2)$

2.2.2 Classifier

　　基於圖級表示，我們使用帶有引數 $\theta_{C}$ 的全連線層進行預測：

　　　　$C^{(l+1)}=\operatorname{Softmax}\left(\sigma\left(C^{(l)} \cdot \theta_{C}^{(l)}\right)\right)\quad\quad\quad\quad(3)$

　　其中，$C^{(l)}$ 表示第 $l$ 層的嵌入，輸入層 $C^{(0)}=H^{O}$ 或 $C^{(0)}=H^{A}$ 分別表示原始表示和增強圖表示。實驗中，採用了一個 2 層多層感知器，得到了對原始表示 $H^{O}$ 和增強表示 $H^{A}$ 的預測 $C^{O}$ 和 $C^{A}$。

2.2.3 Label-invariant Augmentation

　　不對圖級表示做資料增強，而是在原始圖級表示$H^{O}$上做微小擾動得到增強圖級表示。

　　在實驗中，首先計算所有圖的原始表示的質心，得到每個原始表示與質心之間的歐氏距離的平均值為 $d$，即：

　　　　$d=\frac{1}{N} \sum_{i=1}^{N}\left\|H_{i}^{O}-\frac{1}{N} \sum_{j=1}^{N} H_{j}^{O}\right\|\quad\quad\quad\quad(4)$

　　然後計算增強圖表示 $H^{A}$：

　　　　$H^{A}=H^{O}+\eta d \Delta\quad\quad\quad\quad(5)$

　　其中 $\eta$ 縮放擾動的大小，$\Delta$ 是一個隨機單位向量。

　　為實現標籤不變增強，每次，隨機生成多個擾動，並選擇符合標籤不變屬性的合格候選增強。在這些合格的候選物件中，選擇了最困難的一個，即最接近分類器的決策邊界的一個，以提高模型的泛化能力。

2.2.4 Projection Head

　　使用帶有引數 $\theta_{P}$ 的全連線層，從圖級表示中得到對比學習的投影，如下所示：

　　　　$P^{(l+1)}=\sigma\left(P^{(l)} \cdot \theta_{P}^{(l)}\right) \quad\quad\quad\quad(6)$

　　採用一個 2 層多層感知器，從原始表示 $H^{O}$ 和增廣表示 $H^{A}$ 中得到投影 $P^{O}$ 和 $P^{A}$。

2.2.5 Objective Function

　　目標函數包括對比損失和分類損失。對比損失採用 NT-Xent，但只保留正對部分如下：

　　　　$\mathcal{L}_{P}=\frac{-\left(P^{O}\right)^{\top} P^{A}}{\left\|P^{O}\right\|\left\|P^{A}\right\|} \quad\quad\quad\quad(7)$

　　對於分類損失，採用交叉熵，其定義為：

　　　　$\mathcal{L}_{C}=-\sum_{i=1}^{c}\left(Y_{i}^{O} \log P_{i}^{O}+Y_{i}^{O} \log P_{i}^{A}\right) \quad\quad\quad\quad(8)$

　　其中，$Y^{O}$ 是輸入圖的標籤，$c$ 是圖類別的數量。本文只計算帶標籤的圖的 $\mathcal{L}_{C}$。$\text{Classifier}$ 的改進將有助於標籤不變的增強，反過來有利於分類器的訓練。

　　結合等式 $\text{Eq.7}$ 和 $\text{Eq.8}$ ，總體目標函數可以寫成如下：

　　　　$\underset{\Theta}{\text{min}} \quad\mathcal{L}_{P}+\alpha \mathcal{L}_{C}\quad\quad\quad\quad(9)$

3 Experiments

3.1 Datasets

3.2 Semi-supervised graph classification results

3.3 Algorithmic Performance

3.4 In-depth Exploration

Negative Pairs

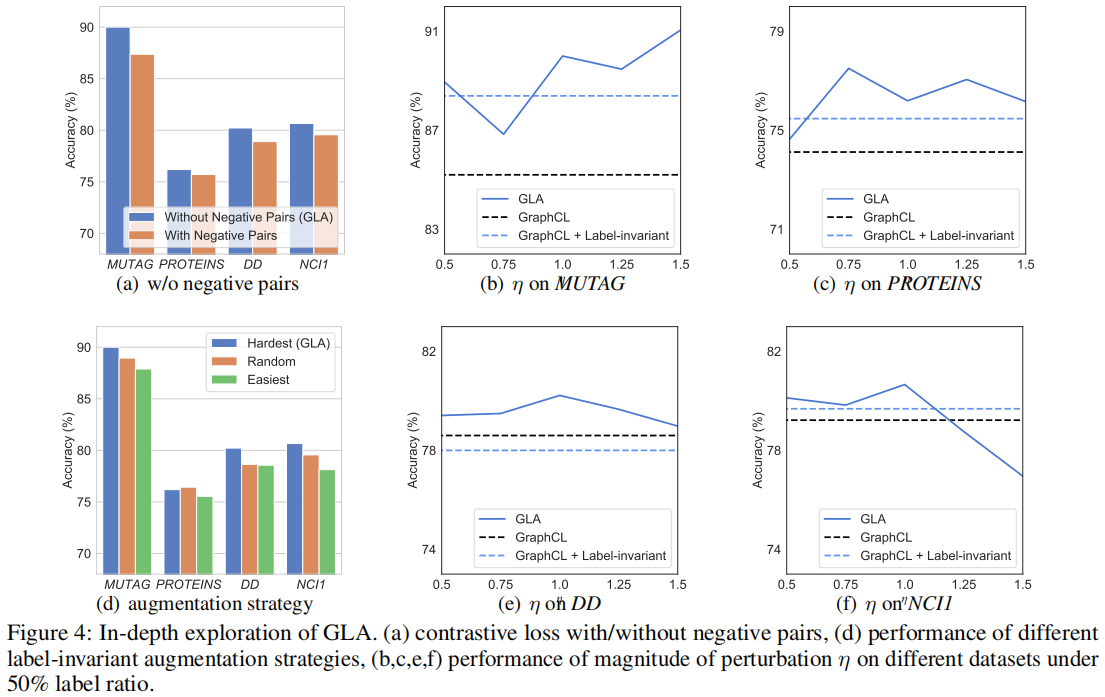
　　現有的圖對比學習方法將來自不同源樣本的增廣圖視為負對，並對這些負對採用範例級判別。由於這些方法分離了 pre-train 階段和 fine-tuning 階段，因此負對包含了來自不同源樣本的增強樣本，但在下游任務中具有相同的類別。

　　Figure 4(a) 顯示了我們在四個資料集上有負對和沒有負對的 GLA 的效能。可以看到，與沒有負對的預設設定相比，有負對的效能顯著下降，而負對在所有四個資料集上都表現一致。與現有的圖對比方法不同，GLA 整合了預訓練階段和微調階段，其中以自監督的方式設計的負對不利於下游任務。這一發現也與最近的[10,9]在視覺對比學習領域的研究結果相一致。

4 Conclusion

　　本文研究了圖的對比學習問題。從現有的方法和訓練前的方法不同，我們提出了一種新的圖示籤不變增強（GLA）演演算法，該演演算法整合了訓練前和微調階段，通過擾動在表示空間中進行標籤不變增強。具體來說，GLA首先檢查增廣表示是否服從標籤不變屬性，並從合格的樣本中選擇最困難的樣本。通過這種方法，GLA在不生成任何原始圖的情況下實現了對比增強，也增加了模型的泛化。在8個基準圖資料集上的半監督設定下的廣泛實驗證明了我們的GLA的有效性。此外，我們還提供了額外的實驗來驗證我們的動機，並深入探討了GLA在負對、增強空間和策略效應中的影響因素。

論文解讀（GLA）《Label-invariant Augmentation for Semi-Supervised Graph Classification》