珂朵莉樹學習筆記

0x00 前言
0x01 關於其命名
最開始出現在 Codeforces Round #449 (Div. 1) C題 上,這位珂學家在題解中用了一種玄學的資料結構解題,開始命名為 ODT樹(Old Driver Tree,老司機樹,以出題者的ID命名),後來普遍稱為珂朵莉樹。
0x02 能解決的問題
珂朵莉樹用於解決含有區間平推操作(即將區間上的數全部變為一個數)的問題時卓有成效,在資料隨機的情況下,用 set 實現複雜度為 \(O(N \ log \ log \ N)\),用連結串列實現複雜度為 \(O(N \ log \ N)\),比同類問題其他演演算法更優。時間複雜度證明請移步這篇文章。
0x03 前置知識
0x10 正文
本文使用 Codeforces Round #449 (Div. 1) C題 作為例題講解珂朵莉樹。
0x11 題意
-- 威廉...
-- 怎麼了?
-- 瑟尼歐里斯好像出了什麼問題...
-- 我會看看的...

瑟尼歐里斯是一把由特殊護符按特定順序排列組成的劍。
已經 \(500\) 年過去了,現在劍的狀態很差,所以威廉決定檢查一下。
瑟尼歐里斯由 \(n\) 片護符組成,威廉把它們排成一列,每個護符上有一個數位 \(a_i\)。
為了保養它,威廉需要進行 \(m\) 次操作。
這裡有四種操作:
- \(1 \ l \ r \ x\) : 將區間 \([l, r]\) 上的數加上 \(x\)。
- \(2 \ l \ r \ x\) : 將區間 \([l, r]\) 上的數全部變為 \(x\)。
- \(3 \ l \ r \ x\) : 查詢區間 \([l, r]\) 的第 \(x\) 大數。
- \(4 \ l \ r \ x \ y\) : 查詢區間 \([l, r]\) 上的數的 \(x\) 次方之和對 \(y\) 取模的值。
本題輸入較為特殊,輸入格式如下:
一行四個整數,分別為 \(n\),\(m\),\(seed\),\(vmax\),前兩個變數意義如題目所述,後兩個變數用於生成亂資料,資料生成虛擬碼如下
def rnd():
ret = seed
seed = (seed * 7 + 13) mod 1000000007
return ret
for i = 1 to n:
a[i] = (rnd() mod vmax) + 1
for i = 1 to m:
op = (rnd() mod 4) + 1
l = (rnd() mod n) + 1
r = (rnd() mod n) + 1
if (l > r):
swap(l, r)
if (op == 3):
x = (rnd() mod (r - l + 1)) + 1
else:
x = (rnd() mod vmax) + 1
if (op == 4):
y = (rnd() mod vmax) + 1
0x12 珂朵莉樹基本思路
由於資料隨機,所以在區間平推操作中區間長度普遍不會太短,所以區間總個數不會太多,於是我們就考慮維護每一個這樣連續的區間,區間中的數都相同。
0x13 結構體定義
用一個結構體來維護每一個區間的資訊。
struct node {
ll l, r; //區間左右端點
mutable ll v; //區間單個元素值
node(ll l, ll r, ll v) : l(l), r(r), v(v) {}
bool operator< (const node &a) const { return l < a.l; }
};
在上述定義中有下面一點需要注意:
- 因為元素值並不是固定的,所以一定要用 mutabel 讓元素值可變起來
0x14 初始化
#include<set>
set<node> tree;
這樣你就得到了一顆啥也沒有的珂朵莉樹。
0x15 spilt操作
因為一個區間上的數不一定自始至終都是一樣的,所以我們需要一個分割函數將區間分隔開,這就是 spilt 函數。
這個操作是珂朵莉樹的核心操作之一,此函數有一個引數,表示要分裂的位置,我們先看程式碼,再解釋它的運作過程。
auto spilt(ll pos) {
auto it = tree.lower_bound(node(pos, 0, 0));
if(it != tree.end( ) && it -> l == pos) return it;
it--;
ll l = it -> l, r = it -> r, v = it -> v;
tree.erase(it);
tree.insert(node(l, pos - 1, v));
return tree.insert(node(pos, r, v)).first;
}
首先,我們要找到一個左端點大於等於 \(pos\) 的區間,用一個迭代器指向它(注意,如果你使用的是c++11,auto 必須要換成 set<node>::iterator),如果當前區間的左端點等於 \(pos\) (並且這個區間要存在)那就說明當前區間不用分割,直接返回當前迭代器,否則就向前跳轉到前一個區間,並將其分割為 \([l, pos - 1]\) 和 \([pos, r]\) 兩個區間。
0x16 assgin操作
珂朵莉樹的核心操作之二,也就是區間平推操作。
有了 spilt 函數,我們的實現也簡單了很多,依舊是對著程式碼解釋。
void assgin(ll l, ll r, ll v) {
auto end = spilt(r + 1), start = spilt(l);
tree.erase(start, end);
tree.insert(node(l, r, v));
}
實現思路沒什麼好講的,無非就是斷開需要賦值的區間,全部刪除再加入一個新的區間,重點在 spilt 的順序上。
看上去貌似和順序沒什麼關係,如果單從邏輯上看確實如此,但是如果從實現上去看就會發現問題。
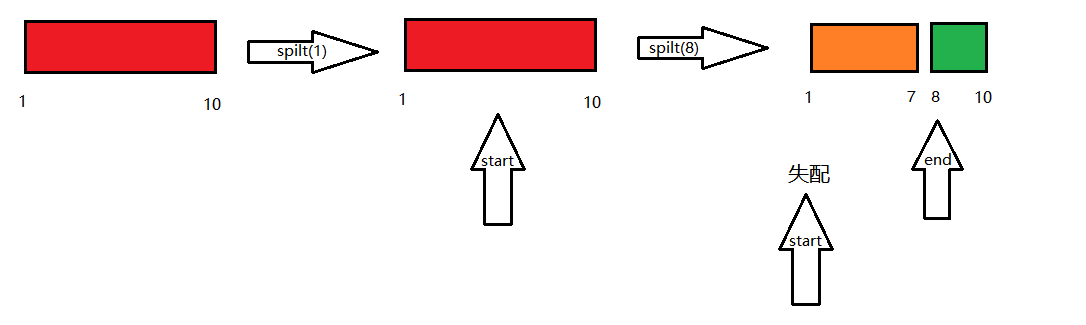
假設我們要從區間 \([1, 10]\) 裡擷取出 \([3, 7]\),我們先執行 spilt(1),現在 start 迭代器指向的是區間 \([3, 10]\),然後我們再執行 spilt(8),end 則指向了區間 \([8,10]\),此時我們發現 start 指向的迭代器被第二次 spilt 操作 erase 掉了,所以呼叫時可能會 RE。(之所以是可能,是因為這東西比較玄學,有可能一會 RE,一會 AC,為了避免這種麻煩,還是規範寫法較為穩妥)
如果還是不理解,就結合下圖再多看幾遍上一段。
0x17 其他程式碼實現
核心程式碼就上面兩個,剩下的亂搞就行。
void add(ll l, ll r, ll x) { //區間加操作
auto end = spilt(r + 1), start = spilt(l);
for(auto it = start; it != end; it++)
it -> v += x; //mulable的作用在此
}
struct Rank {
ll num, cnt; // 值與數量
Rank(ll num, ll cnt) : num(num), cnt(cnt) {}
bool operator< (const Rank &a) const { return num < a.num; }
};
ll get_rank(ll l, ll r, ll x) { //求區間第 x 大數
auto end = spilt(r + 1), start = spilt(l);
vector<Rank> vec;
for(auto it = start; it != end; it++) vec.push_back(Rank(it -> v, it -> r - it -> l + 1));
sort(vec.begin( ), vec.end( )); //將區間上的所有數排序,以便後續暴力查詢
int i;
for(i = 0; i < vec.size( ); i++) {
if(vec[i].cnt < x) x -= vec[i].cnt;
else break;
}
return vec[i].num;
}
ll get_power(ll l, ll r, ll x, ll y) { //求區間 x 次方和 mod y 的值
auto end = spilt(r + 1), start = spilt(l);
ll ans = 0;
for(auto it = start; it != end; it++) ans = (ans + power(it -> v, x, y) * (it -> r - it -> l + 1) % y) % y; //power 為快速冪函數
return ans;
}
0x17 完整程式碼
請在確保自己理解上述所有內容的情況下閱讀
#include<algorithm>
#include<iostream>
#include<vector>
#include<cstdio>
#include<set>
using namespace std;
typedef long long ll;
const int MOD = 1e9 + 7;
ll n, m, seed, vmax;
struct node {
ll l, r;
mutable ll v;
node(ll l, ll r, ll v) : l(l), r(r), v(v) {}
bool operator< (const node &a) const { return l < a.l; }
};
struct Rank {
ll num, cnt;
Rank(ll num, ll cnt) : num(num), cnt(cnt) {}
bool operator< (const Rank &a) const { return num < a.num; }
};
set<node> tree;
ll rnd( );
auto split(ll pos);
void add(ll l, ll r, ll x);
ll power(ll a, ll b, ll p);
void assgin(ll l, ll r, ll v);
ll get_rank(ll l, ll r, ll x);
ll get_power(ll l, ll r, ll x, ll y);
int main( ) {
cin >> n >> m >> seed >> vmax;
for(int i = 1; i <= n; i++) tree.insert(node(i, i, rnd( ) % vmax + 1));
for(int i = 1; i <= m; i++) {
ll op, l, r, x, y;
op = rnd( ) % 4 + 1;
l = rnd( ) % n + 1;
r = rnd( ) % n + 1;
if(l > r) swap(l, r);
if(op == 3) x = rnd( ) % (r - l + 1) + 1;
else x = rnd( ) % vmax + 1;
if(op == 4) y = rnd( ) % vmax + 1;
if(op == 1) add(l, r, x);
if(op == 2) assgin(l, r, x);
if(op == 3) cout << get_rank(l, r, x) << endl;
if(op == 4) cout << get_power(l, r, x, y) << endl;
}
return 0;
}
auto spilt(ll pos) {
auto it = tree.lower_bound(node(pos, 0, 0));
if(it != tree.end( ) && it -> l == pos) return it;
it--;
ll l = it -> l, r = it -> r, v = it -> v;
tree.erase(it);
tree.insert(node(l, pos - 1, v));
return tree.insert(node(pos, r, v)).first;
}
void assgin(ll l, ll r, ll v) {
auto end = spilt(r + 1), start = spilt(l);
tree.erase(start, end);
tree.insert(node(l, r, v));
}
void add(ll l, ll r, ll x) {
auto end = spilt(r + 1), start = spilt(l);
for(auto it = start; it != end; it++)
it -> v += x;
}
ll get_rank(ll l, ll r, ll x) {
auto end = spilt(r + 1), start = spilt(l);
vector<Rank> vec;
for(auto it = start; it != end; it++) vec.push_back(Rank(it -> v, it -> r - it -> l + 1));
sort(vec.begin( ), vec.end( ));
int i;
for(i = 0; i < vec.size( ); i++) {
if(vec[i].cnt < x) x -= vec[i].cnt;
else break;
}
return vec[i].num;
}
ll get_power(ll l, ll r, ll x, ll y) {
auto end = spilt(r + 1), start = spilt(l);
ll ans = 0;
for(auto it = start; it != end; it++) ans = (ans + power(it -> v, x, y) * (it -> r - it -> l + 1) % y) % y;
return ans;
}
ll power(ll a, ll b, ll p) {
ll res = 1, base = a % p;
while(b) {
if(b & 1) res = (res * base) % p;
base = (base * base) % p;
b >>= 1;
}
return res;
}
ll rnd( ) {
ll res = seed;
seed = (seed * 7 + 13) % MOD;
return res;
}
0x18 小結
珂朵莉樹的核心其實就二十行左右的程式碼,並不是什麼很難的演演算法,但是由於其對於資料的要求,很少有題將其作為正解,但是考場騙分還是很有用的。
0x19 習題
- CF915E Physical Education Lessons
- P4344 [SHOI2015]腦洞治療儀
- P3740 [HAOI2014]貼海報
- P4979 礦洞:坍塌
- CF343D Water Tree(涉及到樹鏈剖分)
0x20 後記
本文是本蒟蒻近期學習了珂朵莉樹,為了鞏固所以寫下了這篇學習筆記,如果有紕漏請指出。
另外感謝本文用到的所有資料的提供者。
還有,珂朵莉太可愛了~