AlphaTensor論文閱讀分析

目前只是大概瞭解了AlphaTensor的思路和效果，完善ing

deepmind部落格在 https://www.deepmind.com/blog/discovering-novel-algorithms-with-alphatensor

論文是 https://www.nature.com/articles/s41586-022-05172-4

解決"如何快速計算矩陣乘法"的問題

問題建模

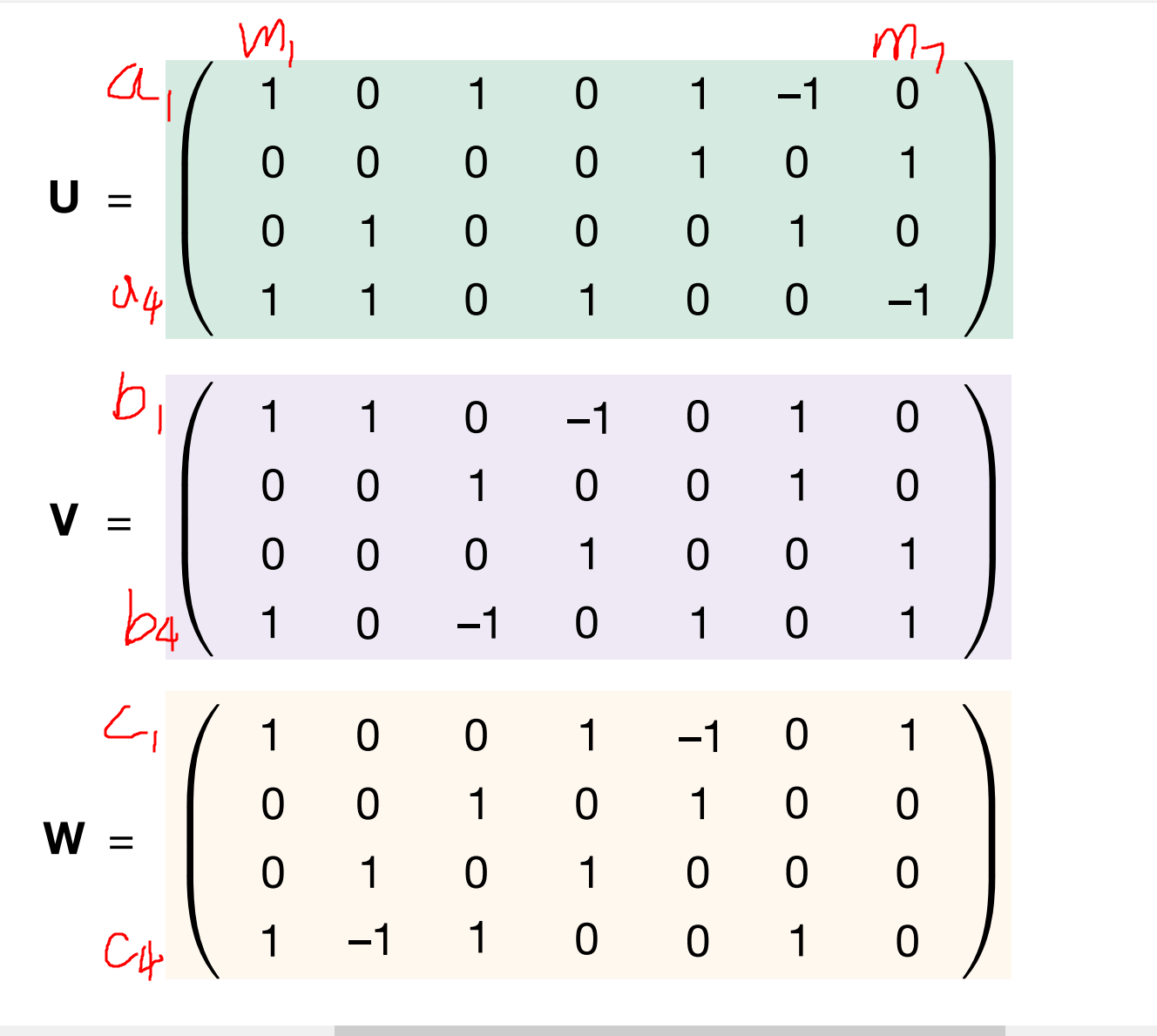
變成single-player game

\[\tau_n= \sum_{r=1}^R \textbf{u}^{(r)} \otimes \textbf{v}^{(r)} \otimes \textbf{w}^{(r)} \]

In $2*2*2$ case of Strassen, R is 7. (see the fig.c). The goal of DRL algorithm is to minimize R (i.e. total step)

the size of $\textbf{u}^{(r)} $ is $(n^2, R)$.

$ \textbf{u}^{(1)}$ is the first column of u: $(1,0,0,1)^T$

$ \textbf{v}^{(1)}$ is the first column of v: $(1,0,0,1)^T$

$\textbf{u}^{(1)} \otimes \textbf{v}^{(1)} = $

\[\begin{bmatrix} 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\1 & 0 & 0 & 1 \end{bmatrix}\quad \]

上面矩陣的第一行代表a1，第四行代表a4，第一列代表b1... (1,1)位置出現一個1，表示當前矩陣代表的式子裡面有個$a_1b_1$ ，上面這個矩陣對應的是m1=(a1+a4)(b1+b4)

$\textbf{u}^{(1)} \otimes \textbf{v}^{(1)} \otimes \textbf{w}^{(1)} $ 就是再結合上ci，哪些ci中包括m1這一項。最終三者外積得到的是$n*n*n$的張量，ci對應的$n*n$矩陣內記錄的就是ci需要哪些ab的乘積項來組合出來。當然，最終需要R個這樣的三維張量才能達到正確的矩陣乘法。

(第一步是選擇mi如何由ai bi組成，這對應上面那個$n*n$的矩陣。第二步是選擇ci如何由mi組成，這對應著$\textbf{w}$那個$(n^2, R)$的矩陣。兩步合在一起得到R個$n*n*n$的三維張量，R個三維張量加起來得到$\tau_n$，$\tau_n$中挑出ci那一維，對應的矩陣就是ci如何由ai bi組成)。

按照樸素矩陣乘法，$c_1=a_1*b_1+a_2*b_3$ ，因此，無論採用什麼路徑，合計出來的三維張量$\tau_n$，在c1這個維度上都必須是

\[\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \end{bmatrix}\quad \]

因此，可以用樸素矩陣乘法算出最終的目標，即$\tau_n$ 。

step

在step 0, $S_0=\tau_n$. (target)

在遊戲的step t, player選擇一個三元組 $(u^{(t)}, v^{(t)}, w^{(t)})$ : $S_t \leftarrow S_{t-1} - \textbf{u}^{(t)} \otimes \textbf{v}^{(t)} \otimes \textbf{w}^{(t)} $

目標是用最少的步數達到zero tensor $S_t=\vec 0$

所以 action space 是 $\{0,1\}^{n^2} \times \{0,1\}^{n^2} \times \{0,1\}^{n^2}$

為了避免遊戲被拉得太長: $R \le R_{limit}$ ( $R_{limit}$ 步之後終止)

reward:

每一個step: -1 reward （為了找到最短路）

如果在non-zero tensor終止: $-\gamma(S_{R_{limit}})$ reward
($\gamma(S_{R_{limit}})$ 是terminal tensor的rank的上界)

constrain $\{u^{(t)}, v^{(t)}, w^{(t)}\}$ in a user-specified discrete set of coeffients F

AlphaTensor

有些類似於 AlphaZero

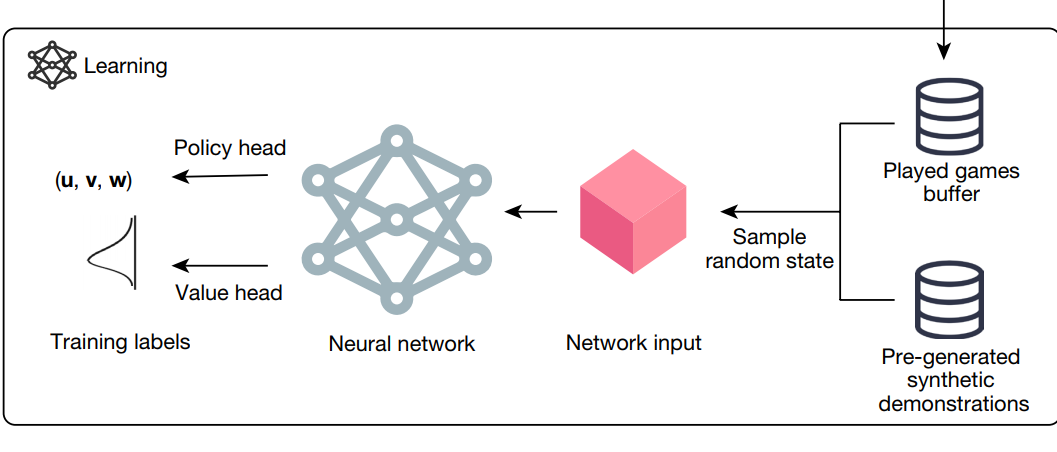
一個deep nn 去指導 MCTS.
state作為輸入, policy (action上的一個概率分佈) 和 value作為輸出

算出最優策略下每一步的action: $\{(u^{(r)}, v^{(r)}, w^{(r)})\}^R_{r=1}$ 之後，就可以拿uvw用於矩陣乘法了

效果

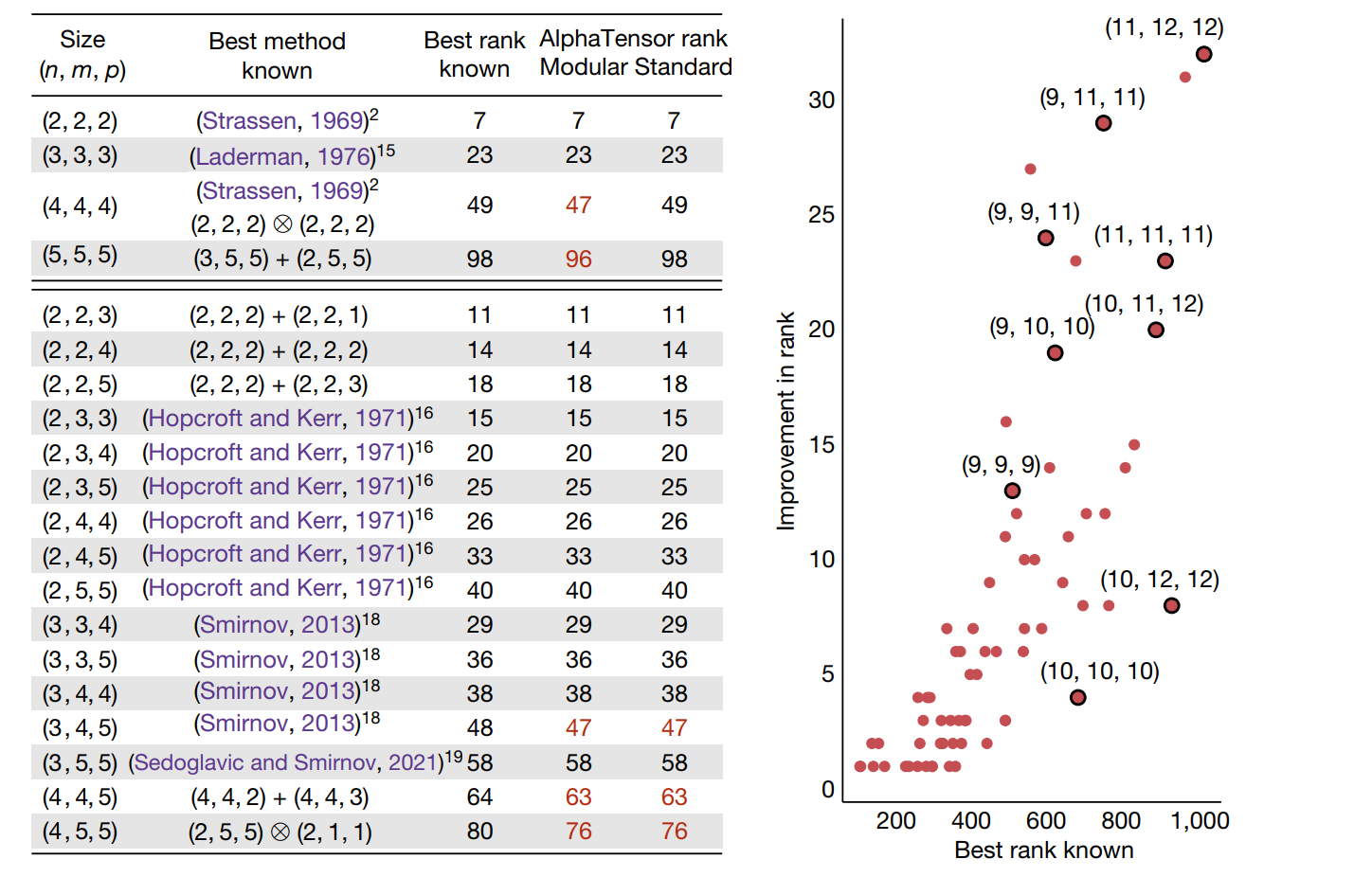
可以看到，AlphaTensor搜尋出來的計算方法，在部分矩陣規模上達到了更優的結果，即乘法次數更少。

在第四行，(5,5,5)情形下的矩陣乘法，AlphaTensor計算出來的方法可以在部落格里面看到，非常複雜，為了減少兩次乘法，卻耗費了數幾十次加法。因此AlphaTensor只能做到漸進時間複雜度更優，在大矩陣情形下達到更快的速度。

值得關注的是，他們在$8192*8192$的方陣乘法上進行了測試，採用$4*4$分塊的方式（這樣每個子矩陣的大小就是$2048*2048$規模的了），AlphaTensor方法比Strassen的方法減少了兩次矩陣乘法，因此加速比從1.043提升至1.085。這說明這一方法相比coppersmith-winograd方法($O(n^{2.37})$)那種銀河演演算法更加實用，常數更低，在8192規模的矩陣就能生效了。而且，計算矩陣乘法的Algorithm 1也方便在GPU和TPU上並行。