論人類下一代語言的可能—4.2算術後的發展

算術是數學中最古老的部分之一。在最初的算術、幾何之後，數學發展出了更多的分支內容：代數、分析、拓撲、概率……本節的講述涉及其中代數、分析的初等部分的內容。其中會講到的一個問題是數學構建的虛擬性質。

算術之後，數學的發展首先是體現在「數」概念的擴充套件上。

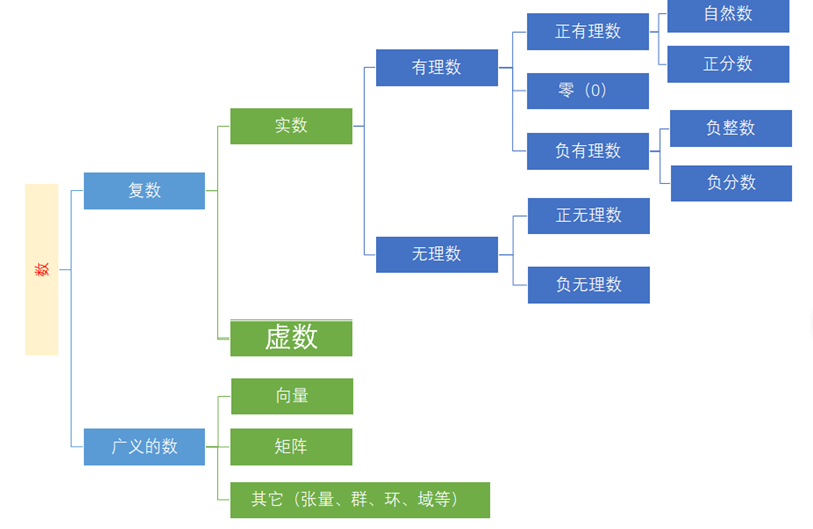
（圖4-2：數系）

其次，數學的發展也體現在計算型別的擴充套件，從四則運算，到平方、開方、指數、對數的運算，微分、積分的運算……不同型別的數與不同型別的計算組成不同的計算系統，數學就是研究各種型別計算系統的性質與規律，並進一步抽象得到更一般的結構與關係。

就像在算術裡一樣，符號的恰當選擇，表示上的進步，對數學各分支的發展也至關重要。字母符號的採用，使數學從算術進入到代數。早期的代數都是一個一個具體的問題，問題的求解也是各自獨立的方法，問題描述與解題過程的說明都是文字的敘述，這時的代數也稱為修辭代數。古希臘亞歷山大港的數學家丟番圖（Diophantus，246-330）開始自覺地使用從文字縮寫或簡寫得到的符號來代表數，並使用字母來代表未知數，他開創的代數也稱為縮寫代數。現代意義上的符號代數，以字母來代表已知數、未知數，應用特定的運運算元號以及等號的代數是文藝復興時期產生的。早期重要的倡導者是法國數學家韋達（法語François Viète，1540－1603），他被稱為現代符號代數之父。符號上的變化帶來研究上的變化，以前一個一個的具體問題可以歸為不同的方程，可以針對每類方程尋求統一的解題方法，運算規律可以以一般形式表達。歷史上萊布尼茨與牛頓幾乎同時發明了微積分，相較牛頓微積分，萊布尼茨對微積分符號的設計與選用有著更多考慮。他引入了微分符號dx、dy，將字母S（Summa）拉長得到「∫」作為積分符號。從效果來說，萊布尼茨的符號系統讓微積分的概念與運算更加清晰，今天所用的微積分符號就是源自萊布尼茨的工作。萊布尼茨說到：「要發明，就要挑選恰當的符號，要做到這一點，就要用含義簡明的少量符號來表達和比較忠實地描繪事物的內在本質，從而最大限度地減少人的思維勞動」。

數學各分支早期階段的發展，多是由實際問題推動。為測量土地發展出了最初的幾何學；為進行貿易、分配財產發展出了算術；為了贏得賭博發展出了概率論……數學最初以實用的工具出現。數學進一步的發展則表現出虛擬的性質。比如數系的擴充套件，除了實踐中會遇到不同型別數的問題外，更多是為了讓算術運算、代數運算及其他的運算能夠閉合，使計算規則具有普遍性而不斷構造出的。為了減法運算始終可以施行構造了負數；為了除法運算始終可以施行構造了分數；為了開方運算始終可以施行構造了無理數、虛數，其中虛數是求負數的平方根時引入的……我們從一些實際問題裡建立了一元一次方程：ax+b=0，對此類方程的求解進行了研究。之後不一定需要實際問題的輸入，也不用天才的大腦，從一元一次方程的形式我們容易想到一元二次方程、一元三次方程、二元一次方程、二元二次方程等，然後我們可以去研究不同型別方程的解法。顯然，一元一次方程簡單清晰的表示，是後續擴充套件的良好基礎。

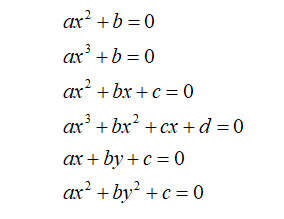
（圖4-3：不同的方程）

在上一節我們把算術看作實物計數計算遷移到符號上形成的結果，其中的關鍵是實物計數的動作，以及由此衍生出的動作系統。從自然數擴充套件到的實數，增加了一類動作系統——進行測量的動作系統。操作代表量度單位的實物來比較被測量的實物，用於形成對連續量的表徵。測量的心理想象是對物件的分割，這種分割可以一直進行下去。如果是測量某一實物的長度，實際的物質可找到更小的構成：分子、原子、質子與中子、電子、更基本的粒子……它們組成的實物並不一定呈均質可無限劃分的情形，這裡分割動作只是心智上有用的假設，或者說，人創造的尺度。目前我們發展出的此類動作系統就只有這二類，可以合稱為計量。

分割的心理想象涉及「無限」的問題，這也是數學裡的一個核心問題。無限的問題在算術裡就已出現。現實中我們能遇到的一個自然數只能是特定大小的數，位置記數法規則可表示任意大的自然數，這意味著它總能生成下一個更大的數，或者能生成無限多的自然數。符號的機制與心理想象上都沒有什麼阻止我們無限操作下去。這次是最早在古希臘所提出的「阿喀琉斯永遠追不上烏龜」悖論所提示的問題。測量的分割動作可以無限地進行下去，每一步都得到一個實數，無限分割下去的結果就是得到緻密的實數，但存在那些實數則是說不清的，像超越數這樣的實數，甚至是不能用構造的方法給出表示。實數是微積分的基礎，在微積分的計算中，計算過程也是同樣的性質，計算可以一直進行，不是操作到某一步就得到結果，也不是沒有結果，結果作為一種極限存在，可以在無盡的操作中無限逼近這一結果，但不會真正達到這一結果。分析上，我們採用大於、小於這些概念描述逼近極限的過程，這邏輯上沒有問題，但這裡存在的非構造性一直是理解上的一個困難。

隨著數學的發展，基於視覺符號的數學本身與計算工具的關係也發生了改變。各種新型的數與計算首先是在數學裡發展起來，如對數、指數的計算，三角函數的計算，微分、積分的計算……就算有紙筆媒介系統的輔助，這些計算對人而言也是困難、枯燥的。發明計算工具來快速、可靠地完成各型別的計算，是各個時代科研與生產上的需要。各種計算工具也應運而生：算盤、計算尺、帕斯卡加法器、萊布尼茨乘法器、巴貝奇的差分機……從木製的工具，到機械的工具，再到機電的工具。這些都是各時代心靈手巧的天才們的創造。

包含虛擬性構造的數學，最終可得到實際應用，這是一個不可思議的地方。同樣的數學內容可為不同的領域規律或事實提供描述，並通過計算解釋各種現象或解決各類問題。最先出現於牛頓物理學裡的微積分，在經濟學領域也被用來進行邊際與彈性的分析，求解各種經濟問題中最佳效益值。這符合前面對符號方式的描述，或者說可將數學視為一門語言。數學的廣泛應用，要求數學本身是可靠的。當數學已發展為枝繁葉茂的大樹，其基礎的可信與內部的無矛盾已不是那麼顯而易見。對此所進行的研究是推動數學發展的另一動力。由希爾伯特倡導，人們嘗試將數學各分支進行公理化、形式化的整理，並採用集合論、一階謂詞邏輯等作為通用的描述形式，以此保障各數學分支的可靠性。其成果包括了前述的皮亞諾算術公理系統。不幸的是集合論中發現了悖論，引發了第三次數學危機，危機激發更多的研究，帶來現代數學中那些基礎且抽象的分支，特別重要一個成果是哥德爾不完備定理，這我們後面還會講到。