哈夫曼編碼解碼(資料結構實驗)
哈夫曼樹
定義
- 定義:帶權路徑長度WPL最小的二元樹稱作哈夫曼樹,又叫最優二元樹
- 節點的帶權路徑長度為:從該節點到樹根之間的路徑長度與節點上的權的乘積
- 樹的帶權路徑長度為:所有葉子節點的帶權路徑長度之和
構造方式
大話資料結構:
根據給定的n個權值{ w1,w2,w3,···,wn }構成n棵二元樹的集合F = { T1,T2,T3,···,Tn },其中每棵二元樹Ti中只有一個帶權為wi的根節點,其左右子樹均為空。(其實就是一個節點)
在F中選取兩棵根節點的權值最小的樹作為左右子樹構造一棵新的二元樹,且置新的二元樹的根節點的權值為其左右子樹上根節點的權值之和。
在F中刪除這兩棵樹,同時將新得到的二元樹加入F中。
重複步驟2和3,直到F只含一棵樹為止,這棵樹便是哈夫曼樹。(這個節點便是哈夫曼樹的根節點)
舉個例子:

現在有五個字元ABCDE,權值分別為5, 15, 40, 30, 10
先取出權值最小的兩個字元,分別為 A, E
將它們作為左右子樹構造一棵新的二元樹:

再將A, E從集合F中刪除,將新的得到的N1加入到F中:
N1的權值即為A, E的權值之和:5 + 10 = 15

重複上述步驟,將權值最小的N1和B作為左右子樹構建一棵新的二元樹:
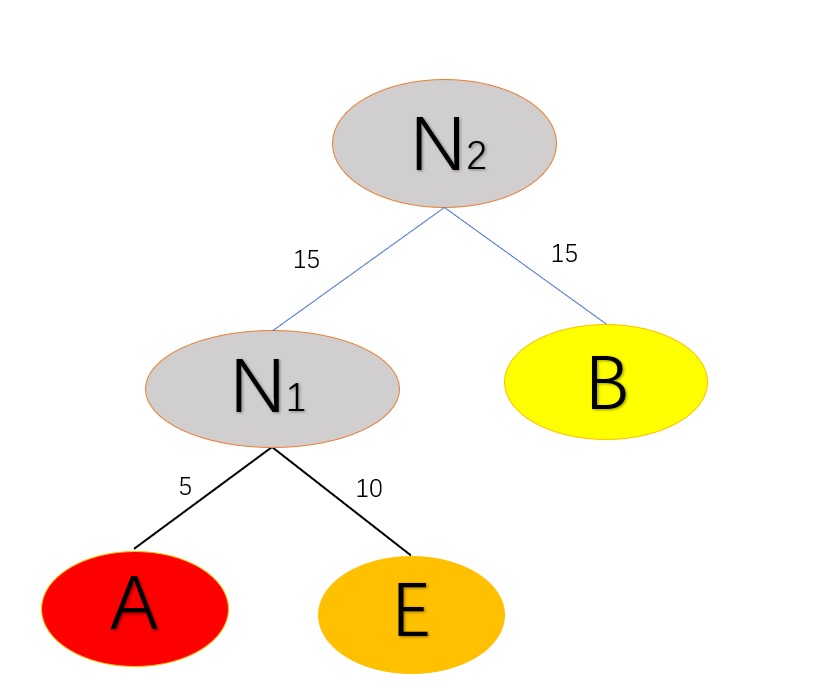
重複上述步驟,將N2加入到集合F中,將N1和B從集合F中刪除,選取F中權值最小的兩個節點分別為N2, D構建新的二元樹:

刪除N2, D,新增N3,選取最小的兩個節點,C和N3作為左右子樹構建二元樹:

這樣,就完成了哈夫曼樹的構造,可以算得:
\(WPL = 5 * 3 + 15 * 3 + 40 * 2 + 30 * 2 + 10 * 2 = 220\)
哈夫曼編碼
將字元的頻率作為權值來構建好的哈夫曼樹,規定左分支為 0,右分支為 1,則從根節點到葉子節點所經過的路徑分支組成的 01序列便為該節點對應字元的編碼,這就是哈夫曼編碼
將上述的哈夫曼樹作為例子,設我們要傳輸的資訊就只有ABCDE這五個字元。
設字元A的頻率為5%,B為15%,C為40%,D為30%,E為10%。
假設我們不用哈夫曼編碼,很自然的想到,我們用二進位制來表示這5個字元:

現在有一段文字內容:CADECDDBACE
二進位制表示:010000011100010011011001000010100
哈夫曼編碼:01000111001000101100001001
很明顯,用哈夫曼編碼傳送資料,節約了儲存。
若編碼為長短不等,那麼必須任一字元的編碼都不是另一個字元的編碼的字首,這種編碼叫字首編碼。
仔細觀察就會發現,哈夫曼編碼不會出現混淆的情況,這是因為每個字元都是在樹上的葉子節點上。
實驗
實驗簡介
實驗專案: 樹形結構及其應用
實驗題目: 哈夫曼編碼與譯碼方法
實驗內容:
哈夫曼編碼是一種以哈夫曼樹(最優二元樹,帶權路徑長度最小的二元樹)為基礎變長編碼方法。其基本思想是:將使用次數多的程式碼轉換成長度較短的編碼,而使用次數少的採用較長的編碼,並且保持編碼的唯一可解性。在計算機資訊處理中,經常應用於資料壓縮。是一種一致性編碼法(又稱"熵編碼法"),用於資料的無失真壓縮。要求實現一個完整的哈夫曼編碼與譯碼系統。
實驗要求:
- 從檔案中讀入任意一篇英文文字檔案,分別統計英文文字檔案中各字元(包括標點符號和空格)的使用頻率;
- 根據已統計的字元使用頻率構造哈夫曼編碼樹,並給出每個字元的哈夫曼編碼(字元集的哈夫曼編碼表);
- 將文字檔案利用哈夫曼樹進行編碼,儲存成壓縮檔案(哈夫曼編碼檔案);
- 計算哈夫曼編碼檔案的壓縮率;
- 將哈夫曼編碼檔案譯碼為文字檔案, 並與原檔案進行比較。
測試結果
test.txt 英文文字測試檔案 test_Copy.txt 英文文字解碼檔案
code.txt 哈夫曼編碼檔案 huffman.txt 哈夫曼樹的結構檔案
一開始,只需要test.txt,內容如下
Hello,I am Az1r!
I come from China.
Now I am a student,and I major in Computer Science.
編碼,譯碼,列印出哈夫曼編碼表:


程式碼
點選檢視程式碼
/*
Author: Az1r
Date: 2022/10/14
*/
#include <iostream>
#include <cstring>
#include <cstdio>
#include <limits>
#include <queue>
#include <map>
#include <fstream>
#include <iomanip>
#define MAX_LENTH 100
using namespace std;
// 哈夫曼樹
struct TreeNode{
int weight;
char ch;
TreeNode* left;
TreeNode* right;
};
typedef TreeNode* Huff;
// 小根堆
struct HeapNode{
Huff* data;
int size;// 堆的大小
int cap; //容量
};
typedef HeapNode* Heap;
Huff T = NULL;
//編碼表
const int N = 128;
int cnt[N];
map<int, string> mp;
Huff CreateNode(char ch, int weight); //建立一個哈夫曼樹的節點
Heap CreateHeap(); //建立一個小根堆
void InitHeap(Heap H); //初始化堆
void SetHeap(Heap H, int p); //向下調整堆
bool IsFull(Heap H); //判滿
bool IsEmpty(Heap H); //判空
bool InsertHeap(Heap H,Huff tree); //向堆中插入插入
Huff Pop(Heap H); //彈出堆中根節點
void LoadTreeByInput(); //通過輸入初始化哈夫曼樹
Huff BuildHuffmanTree(Heap H); //建立哈夫曼樹
void PrintTree(Huff tree); //列印哈夫曼樹
void Menu(); //列印選單
void CreateDict(Huff tree, string temp);//建立哈夫曼編碼表
void PrintCode(); //列印編碼表
void LoadTreeByFile(); //檔案輸入哈夫曼樹
void CodeFile(); //編碼文字檔案
void Caulcute(); //計算壓縮率
void DecodeFile(Huff tree); //解碼文字檔案
/*
test.txt 英文文字測試檔案
test_Copy.txt 英文文字解碼檔案
code.txt 哈夫曼編碼檔案
huffman.txt 哈夫曼樹的結構檔案
*/
int main()
{
int select = -1;
while(select)
{
system("pause");
system("cls");
Menu();
printf("input your choose: ");
scanf("%d", &select);
switch(select)
{
case 1:
{
PrintTree(T);
break;
}
case 2:
{
DecodeFile(T);
break;
}
case 3:
{
CodeFile();
break;
}
case 4:
{
PrintCode();
}
case 5:
{
Caulcute();
break;
}
case 0:
{
break;
}
default:
{
break;
}
}
}
return 0;
}
void Menu()
{
printf("---- Menu ----"); printf("\n");
printf("---- 1.PrintTree ----"); printf("\n");
printf("---- 2.Decode ----"); printf("\n");
printf("---- 3.Code ----"); printf("\n");
printf("---- 4.PrintDictCode ----"); printf("\n");
printf("---- 5.Caulcute ----"); printf("\n");
printf("---- 0.Exit ----"); printf("\n");
}
void Caulcute()
{
int chTotal = 0;
int hfmTotal = 0;
for(int i = 0; i < N; i ++ )
{
chTotal += cnt[i];
hfmTotal += cnt[i] * mp[i].length();
}
double rate = hfmTotal * 1.0 / ( 8 * chTotal ) * 100; //1個字元佔8位元
cout << "Code rate: " << rate << "%" << "\n";
}
void DecodeFile(Huff tree)
{
ifstream infile;
infile.open("code.txt");
ofstream outfile;
outfile.open("test_Copy.txt");
if(infile == NULL || outfile == NULL)
{
printf("File open error!\n");
return;
}
char temp;
Huff x = tree;
while(!infile.eof())
{
infile >> temp;
if(infile.fail())//防止讀到最後一個字元
{
break;
}
if(temp == '0') // 左為 0,右為 1
{
x = x->left;
}else
{
x = x->right;
}
if(x->left == NULL && x->right == NULL) // 左右兒子都無,那就是葉子節點,即儲存字元的節點
{
outfile << x->ch;
x = tree;
}
}
infile.close();
outfile.close();
printf("Succeeful decode file!");
}
void CodeFile()
{
for(int i = 0; i < N; i ++ )
{
cnt[i] = 0;
}
ifstream infile;
infile.open("test.txt");
infile >> noskipws; // 控制符,可以讀取空格回車
char ch;
while(!infile.eof())
{
infile >> ch;
if(infile.fail())//防止讀到最後一個字元
{
break;
}
cnt[(int)ch] ++;
}
infile.close();
ofstream outfile;
outfile.open("huffman.txt");
for(int i = 0; i < N; i ++ )
{
if(cnt[i])
{
ch = i;
outfile << ch << cnt[i] << "\n"; //輸出到哈夫曼樹結構檔案中
}
}
outfile.close();
LoadTreeByFile();
CreateDict(T, "");
infile.open("test.txt");
infile >> noskipws;
outfile.open("code.txt");
while(!infile.eof())
{
infile >> ch;
if(infile.fail())//防止讀到最後一個字元
{
break;
}
outfile << mp[(int)ch];
}
infile.close();
outfile.close();
printf("Succeeful code file!");
}
void PrintCode()
{
int total = 0;
for(int i = 0; i < N; i ++ )
{
total += cnt[i];
}
for(int i = 0; i < N; i ++ ) // 輸出字元,頻率,編碼
{
if(cnt[i])
{
float f = cnt[i] * 1.0 / total;
if(i == 10)
{
cout << setw(3) << i << "---- " << "\\n" << " ---- " << fixed << setprecision(3) << f << " " << mp[i] << "\n" ;
}else if (i == 32)
{
cout << setw(3) << i << "---- " << "<space>" << " ---- " << fixed << setprecision(3) << f << " " << mp[i] << "\n" ;
}else
{
cout << setw(3) << i << "---- " << (char)i << " ---- " << fixed << setprecision(3) << f << " " << mp[i] << "\n" ;
}
}
}
}
void CreateDict(Huff tree, string temp)
{
if(tree)
{
if(tree->left == NULL && tree->right == NULL)
{
int idx = tree->ch;
mp[idx] = temp;
}else
{
CreateDict(tree->left, temp + "0");//左 0
CreateDict(tree->right, temp + "1");//右 1
}
}
}
Huff CreateNode(char ch, int weight)
{
Huff Node = (Huff)malloc(sizeof (TreeNode));
Node->ch = ch;
Node->weight = weight;
Node->left = Node->right = NULL;
return Node;
}
// 堆的構建
Heap CreateHeap()
{
Heap Node = (Heap)malloc(sizeof (HeapNode));
Node->data = (Huff *)malloc((MAX_LENTH + 1) * sizeof (Huff));
Node->size = 0;
Node->cap = MAX_LENTH;
Node->data[0] = CreateNode('\0',INT_MIN);
return Node;
}
// 堆的向下調整
void SetHeap(Heap H, int p)
{
int parent, child;
int lenth = H->size;
Huff root = H->data[p];
for(parent = p; parent * 2 <= lenth; parent = child)
{
// 將Child指向Parent的左右子節點中最小者
child = parent * 2;
if((child < lenth) && H->data[child]->weight > H->data[child + 1]->weight){
child++;
}
// 如果child的權重不再小於parent,調整完畢,否則繼續進行調整
if(root->weight <= H->data[child]->weight)
{
break;
}else
{
H->data[parent] = H->data[child];
}
}
H->data[parent] = root;
}
// 初始化最小堆
void InitHeap(Heap H)
{
// 從最後一個節點的父節點開始,一直到根節點1 (0是哨兵節點)
for(int i = H->size / 2; i > 0; i --)
{
SetHeap(H,i);
}
}
// 判空,判滿
bool IsFull(Heap H)
{
return (H->size == H->cap);
}
bool IsEmpty(Heap H)
{
return (H->size == 0);
}
// 插入堆的操作
bool InsertHeap(Heap H,Huff tree)
{
if(IsFull(H))
{
printf("Full Heap!\n");
return false;
}
H->size ++;
int i= H->size;
// i為最後一個位置,然後一層一層向上過濾
for(; H->data[i / 2]->weight > tree->weight; i /= 2)
{
H->data[i] = H->data[i / 2];
}
H->data[i] = tree;
return true;
}
// 從堆中取出最小元素的實現
Huff Pop(Heap H)
{
if(IsEmpty(H))
{
printf("Empty Heap!\n");
return NULL;
}
int parent,child;
int lenth = H->size;
// 取出根節點
Huff rootTree = H->data[1];
// xTree為最後一個元素,同時size-1(因為取出了根節點)
Huff xTree = H->data[H->size --];
// 從根節點下面找出最小的替換上來
for(parent = 1;parent * 2 <= lenth; parent = child)
{
child = parent * 2;
if((child < lenth) && (H->data[child]->weight > H->data[child+1]->weight))
{
child ++;
}
if(xTree->weight <= H->data[child]->weight)
{
break;
}else
{
H->data[parent] = H->data[child];
}
}
H->data[parent] = xTree;
return rootTree;
}
// 哈夫曼樹的構造
Huff BuildHuffmanTree(Heap H)
{
// 假設已經無序的將節點儲存在堆的data中,
// 首先要將堆調整為最小堆
Huff tree;
InitHeap(H);
int size = H->size;
for(int i = 1;i < size; i ++)
{
tree = (Huff)malloc(sizeof (TreeNode));
// 取出兩個最小節點,作為這個節點的左右分支
tree->ch = '\0';
tree->left = Pop(H);
tree->right = Pop(H);
// 計算新的權值
tree->weight = tree->left->weight + tree->right->weight;
// 將這個節點再插入最小堆
InsertHeap(H,tree);
/* test
*/
}
// 取出哈夫曼樹根節點(也就是堆頂節點)
tree = Pop(H);
return tree;
}
// 先序遍歷哈夫曼樹
void PrintTree(Huff tree)
{
if(tree)
{
if((tree->left == NULL) && (tree->right == NULL))
{
char ch = tree->ch;
if(ch == '\n')
{
cout << "Leaf " << setw(3) << tree->weight << " ---- " << "\\n" << "\n" ;
}else if(ch == ' ')
{
cout << "Leaf " << setw(3) << tree->weight << " ---- " << "<space>" << "\n" ;
}else
{
cout << "Leaf " << setw(3) << tree->weight << " ---- " << ch << "\n" ;
}
}else
{
cout << "Node " << setw(3) << tree->weight << "\n" ;
}
PrintTree(tree->left);
PrintTree(tree->right);
}
}
void LoadTreeByFile()
{
ifstream infile;
infile.open("huffman.txt");
if(infile == NULL)
{
printf("load file error!\n");
return;
}
int weight;
char ch;
char temp[20];
Heap heap = CreateHeap();
infile >> noskipws; // 控制符,可以讀取空格回車
while(!infile.eof())
{
infile >> ch;
infile.getline(temp, 20);
weight = atoi(temp);
heap->data[++ heap->size] = CreateNode(ch, weight);
}
infile.close();
T = BuildHuffmanTree(heap);
}
// 哈夫曼樹從使用者輸入
void LoadTreeByInput()
{
printf("please input your haffman:\n");
int weight,count;
char ch;
char temp[10];
Heap heap = CreateHeap();
printf("input data num :");
scanf("%d", &count);
cout << "( data+weight ):" <<endl;
for(int i = 1;i <= count; i ++)
{
scanf("%s", temp);
ch = temp[0];
weight = atoi(temp + 1);
cnt[(int)ch] = weight;
heap->data[i] = CreateNode(ch, weight);
heap->size ++;
}
T = BuildHuffmanTree(heap);
}
一些相關的問題
- 我們現在是將哈夫曼編碼同樣作為文字檔案儲存在.txt檔案中,如何將這些01序列直接儲存到二進位制檔案或者是壓縮檔案呢?1個字元在文字檔案中是佔1個位元組,佔8位元,我們現在將1個字元轉為多個字元(都是01)表示,事實上,是擴大了儲存空間。
- 程式碼中的堆,是手寫的小根堆,也可以使用STL中優先佇列priority_queue來實現。
- 上述 1-5 的編碼和譯碼是基於字元的壓縮,如何考慮基於單詞的壓縮,完成上述工作。
- 上述 1-5 的編碼是二進位制的編碼,如何採用 K 叉的哈夫曼樹完成上述工作,實現「K 進位制」的編碼和譯碼 。
參考資料
-
程傑. 大話資料結構:溢彩加強版[M]. 北京: 清華大學出版社, 2020.
本文來自部落格園,作者:江水為竭,轉載請註明原文連結:https://www.cnblogs.com/Az1r/p/16794068.html