資料統計與視覺化課程總結

大數定理與蒙特卡洛

大數定律的客觀背景

大量隨機試驗中

事件發生的頻率穩定於某一常數
測量值的算術平均值具有穩定性

比如：

大量拋擲硬幣字母使用頻率
正面出現頻率

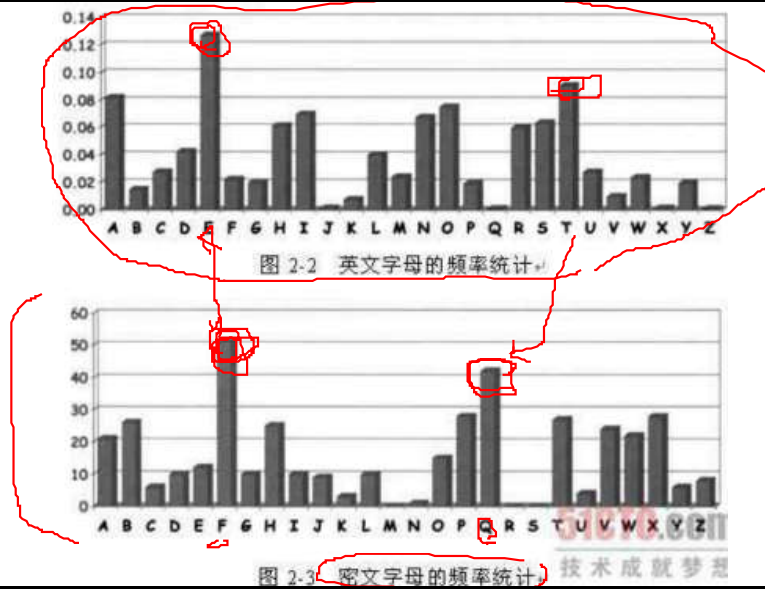
本福特定律

也叫紐科姆-本福德定律，反常數定律，或第一位數定律，是關於許多現實生活中的數位資料中前幾位數位的頻率分佈的觀察。

十進位制中，首位數位出現的概率為：
d，1，2，3，4，5，6，7，8，9
p，30.1%，17.6%，12.5%，9.7%，7.9%，6.7%，5.8%，5.1%，4.6%

中心極限定理（CLT）

中心極限定理是概率論中最著名的結果之一，它不僅提供了計算獨立隨機變數之和的近似概率的簡單方法，而且有助於解釋為什麼很多自然群體的經驗頻率呈現出鐘形曲線這一值得注意的事實。

中心極限定理使得很多引數檢驗成為可能，只要樣本數量足夠多（通常要求>30）即可，底層分布如何沒有關係。因此，t檢驗對正態偏離的魯棒性高。

貝葉斯定理

貝葉斯公式：

\[\begin{eqnarray} P(B \mid A) & = & \frac{P(A \mid B) P(B)}{P(A)} \\ {\text {Posterior}} & = & \frac{\text { likelihood } \times \text { prior }}{\text { evidence }} \end{eqnarray} \]

似然(likelihood)：

\[L(\theta \mid x)=P(X=x \mid \theta) \]

極大似然估計(MLE):

Maximum Likelihood Estimate(MLE):找出引數θ,使得從中抽樣所得的觀測資料的概率最大

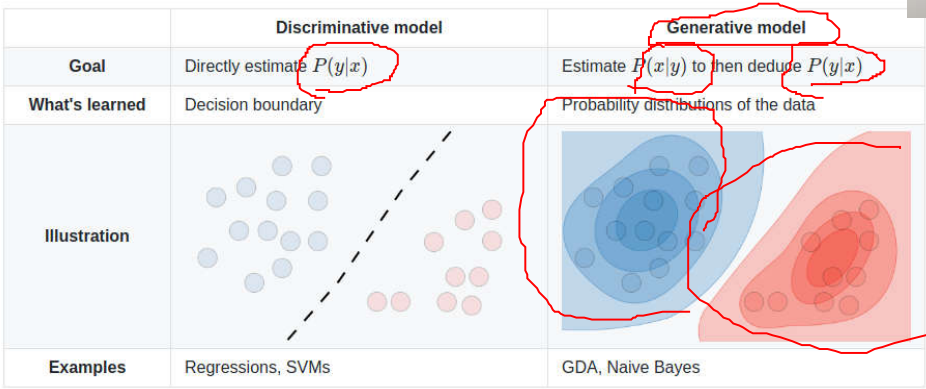
\[L(\theta)=L\left(x_{1}, x_{2}, \ldots, x_{n} ; \theta\right)=\prod_{i=1}^{n} p\left(x_{i} ; \theta\right) \]

判別模型 vs 生成模型

生成模型對資料的生成方式進行建模。它提出一個問題：根據我的生成方式假設，哪個類別$y$最有可能產生當前的特徵$X$？需要對$P(X|Y)$進行建模。判別模型不關心資料是如何生成的，它只是對給定的特徵進行判別/分類。直接對$P(Y|X)$進行建模。

貝葉斯定理應用：

\[p \text { (類別|特徵) }=\frac{p(\text { 特徵|類別 }) p \text { (類別})}{p(\text {特徵) }}\\ p \text { (病因|症狀) }=\frac{p(\text { 症狀|病因 }) p \text { (病因})}{p(\text {症狀) }} \]

概率統計基礎知識

隨機變數

在實際問題中，隨機試驗的結果可以用數量來表示，由此就產生了隨機變數的概念。
隨機變數通常用大寫字母 X,Y,Z,W,N 等表示。
而表示隨機變數所取的值時, 一般採用小寫字母 x, y, z, w, n等。
有了隨機變數, 隨機試驗中的各種事件，就可以通過隨機變數的關係式表達出來。

隨機變數概念的產生是概率論發展史上的重大事件. 引入隨機變數後，對隨機現象統計規律的研究，就由對事件及事件概率的研究擴大為對隨機變數及其取值規律的研究。

我們將研究兩類隨機變數：離散型隨機變數、連續型隨機變數。

離散型隨機變數表示方法（1）公式法（2）列表法。

離散型隨機變數三種常見分佈：

1、（0-1）分佈：（也稱兩點分佈或伯努利分佈）隨機變數X只可能取0與1兩個值，其分佈律為：

\[P\{X=k\}=p^{k}(1-p)^{1-k}, \quad k=0,1 \quad(0<p<1) \]

或：

\[X \sim\left|\begin{array}{cc} 0 & 1 \\ 1-p & p \end{array}\right| \]

2、二項分佈：將伯努利試驗E獨立地重複地進行n次 , 則稱這一串重複的獨立試驗為n重伯努利試驗。

「重複」是指這n次試驗中PA)=p保持不變
「獨立」是指各次試驗的結果互不影響

3、泊松分佈

設隨機變數X所有可能取的值為0 , 1 , 2 , … , 且概率分佈為：$P(X=k)=\frac{\lambda^{k}}{k !} e^{-\lambda}, \quad k=0,1,2, \cdots \cdots,$其中 >0 是常數,則稱 X 服從引數為的$\lambda$泊松分佈,記作X ~ π($\lambda$ )

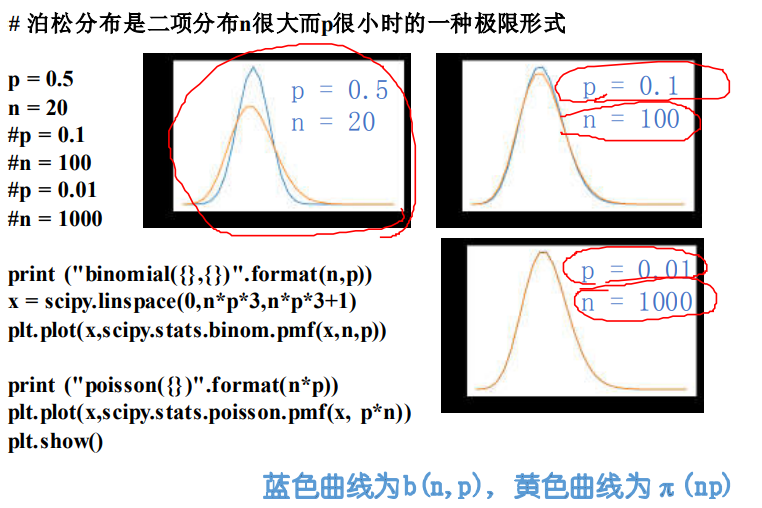
泊松分佈是二項分佈n很大而p很小時的一種極限形式

二項分佈是說，已知某件事情發生的概率是p，那麼做n次試驗，事情發生的次數就服從於二項分佈。

泊松分佈是指某段連續的時間內某件事情發生的次數，而且「某件事情」發生所用的時間是可以忽略的。例如，在五分鐘內，電子元件遭受脈衝的次數，就服從於泊松分佈。（其它例子：一天內，110接到報警的數量；一天內，醫院來掛號的病人數）

假如你把「連續的時間」分割成無數小份，那麼每個小份之間都是相互獨立的。在每個很小的時間區間內，電子元件都有可能「遭受到脈衝」或者「沒有遭受到脈衝」，這就可以被認為是一個p很小的二項分佈。而因為「連續的時間」被分割成無窮多份，因此n(試驗次數)很大。所以，泊松分佈可以認為是二項分佈的一種極限形式。

因為二項分佈其實就是一個最最簡單的「發生」與「不發生」的分佈，它可以描述非常多的隨機的自然界現象，因此其極限形式泊松分佈自然也是非常有用的。

連續型隨機變數三種常見分佈

1.均勻分佈

若r .v X的概率密度為：

\[f(x)=\left\{\begin{aligned} \frac{1}{b-a}, & a<x<b \\ 0, & \text { 其它 } \end{aligned}\right. \]

則稱X在區間( a, b)上服從均勻分佈(uniform)，記作$X$~$U(a, b)$

若$X$~$U(a, b)$:

(1) 對於長度$l$為的區間$(c, c+l), a \leq c<c+l \leq b \text {, }$, 有

\[P\{c<X \leq c+l\}=\int_{c}^{c+l} \frac{1}{b-a} d x=\frac{l}{b-a} \]

(2) $X$的分佈函數為：

\[F(x)=P\{X \leq x\}=\left\{\begin{array}{ll} 0, & x<a \\ \frac{x-a}{b-a}, & a \leq x<b \\ 1 & x \geq b \end{array}\right. \]

2.指數分佈

若r .v X具有概率密度：

\[f(x)=\left\{\begin{array}{ll} \frac{1}{\theta} e^{-\frac{x}{\theta}}, x>0 \\ 0, \qquad \text {其它} \end{array}\right. \]

其中$\theta$> 0為常數, 則稱 X服從引數為$\theta$的指數分佈$X$~$Expo(\theta)$.

指數分佈常用於可靠性統計研究中，如元件的壽命.

若X服從引數為$\theta$的指數分佈, 則其分佈函數為

\[F(x)=P\{X \leq x\}=\left\{\begin{array}{ll} 1-e^{-x / \theta}, & x>0 \\ 0, & \text { 其它 } \end{array}\right. \]

指數分佈常用於可靠性統計研究中，如元件的壽命.

指數分佈具有無記憶性。

\[\begin{array}{c} P\{X>s+t \mid X>s\}=P\{X>t\} . \end{array} \]

3.正態分佈

若連續型r .v X 的概率密度為

\[f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}, \quad-\infty<x<\infty \]

其中μ和σ( σ>0 )都是常數, 則稱$X$服從引數為μ和σ的正態分佈或高斯分佈。記作$X$~$N(\mu, \sigma^2)$

標準正態分佈

μ = 0, σ = 1 的正態分佈稱為標準正態分佈.
其密度函數和分佈函數常用φ($x$) 和Φ($x$) 表示：

\[\begin{array}{l} \varphi(x)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^{2}}{2}},-\infty<x<\infty \\ \Phi(x)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} e^{-\frac{t^{2}}{2}} d t,-\infty<x<\infty \end{array} \]

定理1 若 $X$~$N(\mu, \sigma^2)$ 則 $Z=\frac{X-\mu}{\sigma} \sim N(0,1)$

標準正態分佈的重要性在於，任何一個一般的正態分佈都可以通過線性變換轉化為標準正態分佈.

3$\sigma$ 準則

由標準正態分佈的查表計算可以求得，當$X$~$N(0, 1)$ 時

\[\begin{array}{l} P(|X| \leq 1)=2\Phi(1)-1=0.6826 \\ P(|X| \leq 2)=2\Phi(2)-1=0.9544 \\ P(|X| \leq 3)=2\Phi(3)-1=0.9974 \end{array} \]

這說明，X的取值幾乎全部集中在[-3,3]區間內，超出這個範圍的可能性僅佔不到0.3%.

六西格瑪(six sigma)是一種改善企業質量流程管理的技術，以「零缺陷」的完美商業追求，帶動質量成本的大幅度降低，最終實現財務成效的提升與企業競爭力的突破。

矩(moment)

一階中心距是平均值，二階中心距是方差，三階中心矩是偏度，四階中心距（經過歸一化和轉移）是峰度。

協方差矩陣

類似定義n 維隨機變數$(X_1, X_2, …, X_n) $的協方差矩陣.

若:

\[\begin{aligned} c_{i j}=& \operatorname{Cov}\left(X_{i}, X_{j}\right) \\ =& E\left\{\left[X_{i}-E\left(X_{i}\right)\right]\left[X_{j}-E\left(X_{j}\right)\right]\right\} \\ &(\boldsymbol{i}, j=\mathbf{1}, 2, \ldots, n) \end{aligned} \]

都存在，稱

矩陣 C為$(X_1, X_2, …, X_n)$ 的協方差矩陣

\[C=\left ( \begin{array}{cccc} c_{11} & c_{12} & \cdots & c_{1 n} \\ c_{21} & c_{22} & \cdots & c_{2 n} \\ \vdots & \vdots & \cdots & \vdots \\ c_{n 1} & c_{n 2} & \cdots & c_{n n} \end{array}\right ) \]

數理統計

統計：給出你手中的資訊（樣本），桶（總體）裡有什麼？

概率：給出桶中的資訊，你手裡有什麼？

數理統計可以分為描述性統計和統計推斷，前者側重於總結和說明被觀測資料集合（樣本）的特徵。樣本
是從總體中抽取的，表示與我們實驗相關的相似個體或事件的總集合。與描述性統計相反，統計推斷從給定的樣本中進一步推匯出總體的特徵。

描述性統計：呈現、組織和彙總資料
統計推斷：根據樣本中觀測到的資料得出關於總體的結論

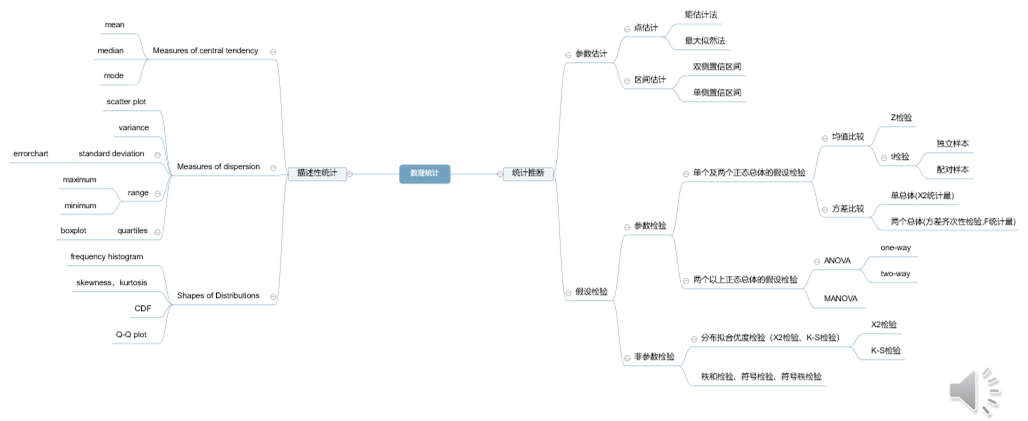
描述性統計是用於資料分析的術語，它有助於以有意義的方式描述、顯示或總結資料，比如資料可能出現的模式。但是，描述性統計並不允許我們在所分析的資料之外得出結論，或者就我們可能做出的任何假設得出結論。它只是描述資料的一種方式。

總體和樣本

總體

一個統計問題總有它明確的研究物件.研究物件的全體稱為總體，總體中每個成員稱為個體，總體中所包含的個體的個數稱為總體的容量.

總體分為有限總體和無限總體.研究某批燈泡的質量

定義：設$X$是具有分佈函數$F$的隨機變數，若$X_1,X_2,...,X_n$是具有同一分佈函數$F$的、相互獨立的隨機變數，則稱$X_1,X_2,...,X_n$為從分佈函數$F$（或總體、或總體）得到的容量$n$為的簡單隨機樣本，簡稱樣本，它們的觀察值$X_1,X_2,...,X_n$稱為樣本值，又稱為$X$的$n$個獨立的觀察值.

樣本及抽樣分佈

統計量

由樣本值去推斷總體情況，需要對樣本值進行「加工」，這就要構造一些樣本的函數，它把樣本中所含的（某一方面）的資訊集中起來.

幾個常見統計量：

樣本平均值、樣本方差、樣本標準差、

樣本k階原點矩：$A_{k}=\frac{1}{n} \sum_{i=1}^{n} X_{i}^{k},k=1,2,...$

樣本k階中心矩：$B_{k}=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{k}$

請注意:

若總體$X$ 的$k$階矩$E\left(X^{{k}\right)=\mu}{k} $ 存在, 則當$n\rightarrow\infty$ 時, $A_{k}=\frac{1}{n} \sum_{i=1}^{n} X_{i}^{k} \stackrel{p}{\longrightarrow} \mu^{k} \quad k=1,2, \cdots $

事實上由$X_1,X_2,...,X_n$獨立且與$X$同分布，有$X_1^k,X_2^k,...,X_n^k$獨立且與$X^k$同分布,$E(X_i^k)=\mu^k$,$k=1,2,...,n$再由辛欽大數定律可得上述結論.

再由依概率收斂性質知，可將上述性質推廣為

\[g\left(A_{1}, A_{2}, \cdots, A_{k}\right) \stackrel{p}{\longrightarrow} g\left(\mu_{1}, \mu_{2}, \cdots, \mu_{k}\right) \]

其中g為連續函數.

這就是矩估計法的理論根據.

統計量（樣本） vs 引數（總體）

樣本的屬性如平均值或者標準差，不稱為引數而是被稱作統計量。推斷統計是使我們能夠利用樣本對樣
本所來自的總體進行概括/推斷的技術。

使用統計量評估引數.

統計三大抽樣分佈

抽樣分佈

如果總體(Population)滿足特定的分佈，那麼其樣本(Sample)（統計量）滿足怎樣的分佈規律？

關於樣本均值的抽樣分佈，如$t$

關於樣本方差的抽樣分佈，如$\chi^2$ 、$F$

1、$\chi^2$ 分佈

$\chi^2$分佈是由正態分佈派生出來的一種分佈.

定義: 設$X_1,X_2,...,X_n$相互獨立, 都服從標準正態分佈$N(0,1)$, 則稱隨機變數：

\[\chi^{2}=X_{1}{ }^{2}+X_{2}{ }^{2}+\cdots+X_{n}{ }^{2} \]

所服從的分佈為自由度為n 的$\chi^2$分佈.

自由度（degree of freedom）記為$\chi^{2} \sim \chi^{2}(n)$

卡方分佈-不同自由度下的PDF曲線(概率密度函數)：

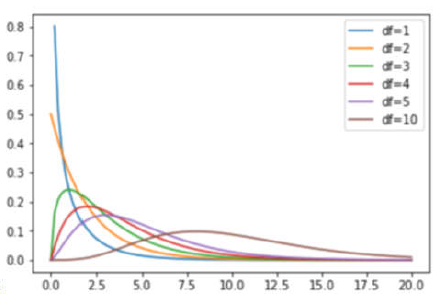
2、$t$ 分佈(學生分佈）

定義: 設$X～N(0,1)$ , $Y～\chi^2$, 且$X$與$Y$相互獨立，則稱變數$t=\frac{X}{\sqrt{Y / n}}$所服從的分佈為自由度為n 的t 分佈.

記為$t\sim t(n)$.

分佈的性質：

具有自由度為$n$的$t$分佈$t\sim t(n)$, 其數學期望與方差為：E(t)=0, D(t)=n /(n-2)(n>2)
即當$n$足夠大時，$t \stackrel{\text { 近似 }}{\sim} N(0,1)$.

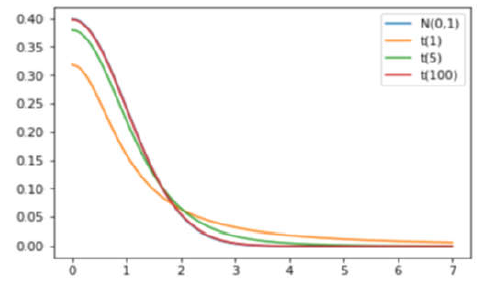
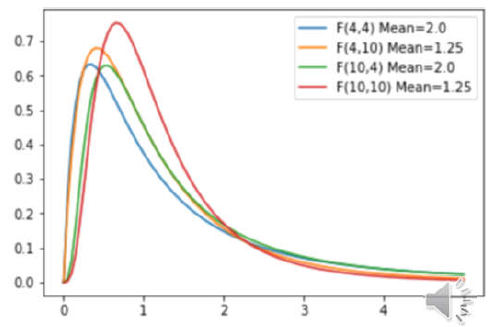
3、F分佈

定義: 設$U \sim \chi^{2}\left(n_{1}\right), V \sim \chi^{2}\left(n_{2}\right)$

$U$與$V$相互獨立，則稱隨機變數$F=\frac{U / n_{1}}{V / n_{2}}$

服從自由度為$n_1$及$n_2$ 的F分佈，$n_1$稱為第一自由度，$n_2$稱為第二自由度，記作$F\sim F(n1,n2)$

由定義可見:

\[\frac{1}{F}=\frac{V / n_{2}}{U / n_{1}} \sim \boldsymbol{F}\left(\boldsymbol{n}_{\mathbf{2}}, \boldsymbol{n}_{\mathbf{1}}\right) \]

F分佈的數學期望為:

\[E(F)=\frac{n_{2}}{n_{2}-2} \quad \text { 若 } \boldsymbol{n}_{\mathbf{2}}>\mathbf{2} \]

即它的數學期望並不依賴於第一自由度$n_1$.