知識圖譜實體對齊2：基於GNN嵌入的方法

1 導引

我們在上一篇部落格《知識圖譜實體對齊1：基於平移(translation)嵌入的方法》中介紹瞭如何對基於平移嵌入+對齊損失來完成知識圖譜中的實體對齊。這些方法都是通過兩個平移嵌入模型來將知識圖譜\(\mathcal{G}_1\)和\(\mathcal{G}_2\)的重疊實體分別進行嵌入，並加上一個對齊損失來完成對齊。不過，除了基於平移的嵌入模型之外，是否還有其它方式呢？

答案是肯定的。目前已經提出了許多基於GNN的實體對齊方法^[1]，這些方法不僅採用GNN捕捉更多的實體結構化資訊，還通過諸如引數共用、引數交換等方式在embedding模組中就使實體的embeddings儘可能統一到一個向量空間。

基於GNN的方法可以被分為基於GCN(graph convolutional network)的和基於GAT(graph attention network)兩類，它們常常使用實體的鄰居知識來對知識圖譜的結構進行編碼，大多數鄰居及被做為嵌入模組的輸入特徵。因為這裡存在一個假定，即對齊的實體將有相似的鄰居。大多數基於GNN的方法在訓練中只使用實體來做為對齊種子，而不是關係來做為對齊種子。

2 基於GNN的方法

2.1 GCN-Align

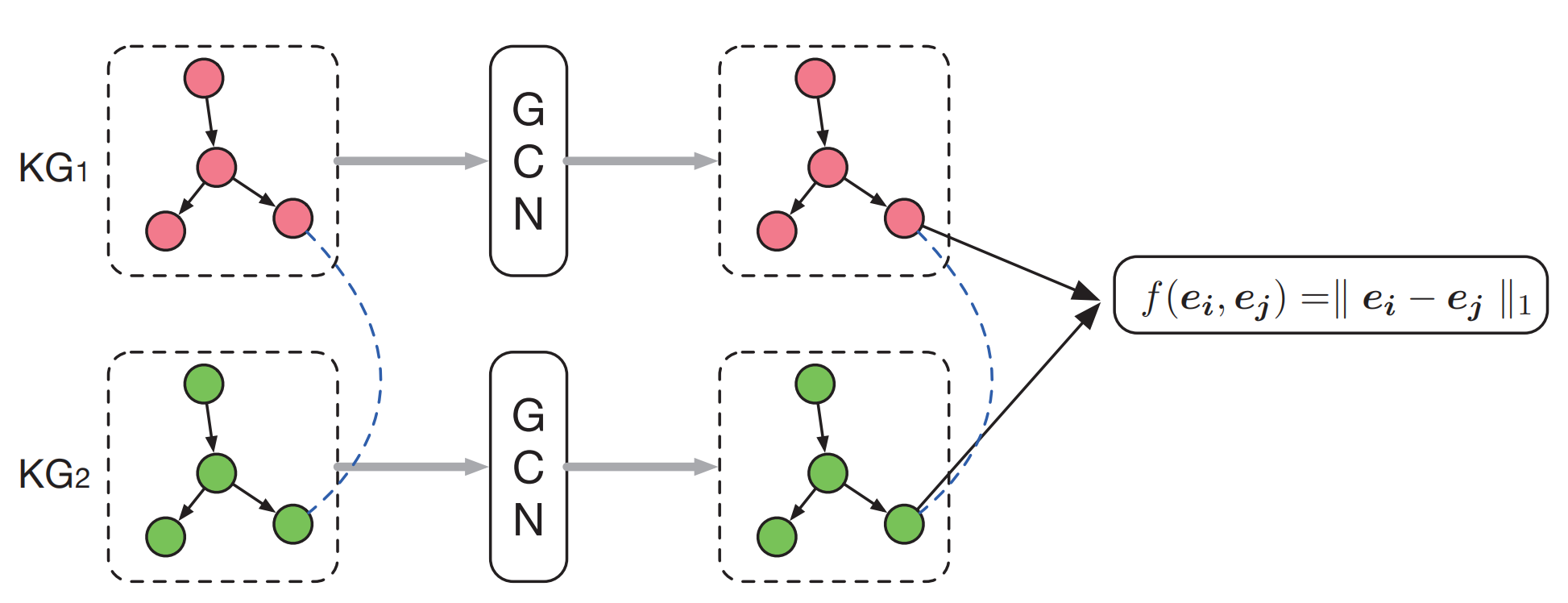
本文是第一篇採用GNN來進行實體對齊的工作^[2]。GCN-Align使用兩個GCN來將\(\mathcal{G}_1\)和\(\mathcal{G}_2\)的實體嵌入到一個統一的向量空間中（這兩個GCN使用共用權重矩陣）。

\[\boldsymbol{H}^{(l+1)}=\sigma\left(\hat{\boldsymbol{D}}^{-\frac{1}{2}} \hat{\boldsymbol{A}} \hat{\boldsymbol{D}}^{-\frac{1}{2}}\boldsymbol{H}^{(l)} \boldsymbol{W}^{(l)}\right) \]

（注：原論文除了實體embeddings，還還有個屬性embedings，我們這裡從簡省略）
這裡\(\boldsymbol{H}^{(l+1)}\)是實體的embeddings，\(\boldsymbol{W}^{(l)}\)是其對應的權重，\(\hat{\boldsymbol{A}}=\boldsymbol{A}+\boldsymbol{I}\)意為帶自環的權重矩陣，\(\hat{\boldsymbol{D}}\)意為\(\hat{\boldsymbol{A}}\)的節點度矩陣（用於歸一化使用）。

不過GCN-Align和GCN有所不同，GCN-Align在計算\(a\in \mathbb{A}\)時還考慮了不同的關係謂詞。新的鄰接矩陣計算如下：

\[a_{i j} \in \boldsymbol{A}=\sum_{\left(e_i, r, e_j\right) \in \mathcal{T}} g_h(r)+\sum_{\left(e_j, r, e_i\right) \in \mathcal{T}} g_t(r) \]

這裡函數\(g_h(r)\)和\(g_t(r)\)計算了由關係\(r\)連線的頭實體和尾實體的數目再除以含有關係\(r\)的實體數量。\(\mathcal{T}\)為知識圖譜中所有元組的集合。\((e_j, r, e_i)\)和\((e_i, r, e_j)\)都是KG中的元組。函數\(g_h(r)\)和\(g_t(r)\)分別計算關係\(r\)所連線的頭實體和尾實體數量。這樣，鄰接矩陣\(\boldsymbol{A}\)就有助於對embedding資訊如何在實體間傳遞進行建模。

然後，GCN-Align的訓練也是由最小化間隔損失（參見我們上一篇部落格《知識圖譜實體對齊1：基於平移(translation)的方法》）來完成，其alignment score function定義為：

\[\begin{aligned} f_{\text {align }}\left(e_1, e_2\right)=& \frac{1}{d}\left.\| \boldsymbol{h}\left(e_1\right)-\boldsymbol{h}\left(e_2\right)\right) \|_{L_1} \end{aligned} \]

這裡\(h(\cdot)\)表示維度為\(d\)的實體嵌入。

整個網路的架構如下：

2.2 HGCN

HGCN^[3]在實體嵌入的過程中隱式地利用關係的表示來改善對齊過程。為了包含關係資訊，HGCN同時學習實體和關係謂詞的embeddings，

其整個包含embedding和align模組的框架如下：

本文提出的框架可分為以下的三個階段：

Stage 1

使用GCN的變種Highway-GCN來將實體嵌入到統一的向量空間。這裡直接將\(\mathcal{G}_1\)和\(\mathcal{G}_2\)視作一個圖\(G_a\)，然後使用一個統一的GCN來獲得\(G_a\)的實體嵌入：

\[\boldsymbol{H}^{(l+1)}=\operatorname{ReLU}\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} \boldsymbol{X}^{(l)} \boldsymbol{W}^{(l)}\right) \]

我們這裡採用逐層的highway gates（高速門）來建立Highway-GCN(HGCN)模型。逐層的highway gates用於控制GCN網路中的前向傳播，寫為以下的函數\(T\)的形式：

\[T\left(\boldsymbol{H}^{(l)}\right)=\sigma\left(\boldsymbol{H}^{(l)} \boldsymbol{W}^{(l)}+\boldsymbol{b}^{(l)}\right)\\ \boldsymbol{H}^{(l+1)}=T\left(\boldsymbol{H}^{(l)}\right) \odot \boldsymbol{H}^{(l+1)}+\left(\mathbf{1}-T\left(\boldsymbol{H}^{(l)}\right)\right) \odot \boldsymbol{H}^{(l)} \]

這裡\(\boldsymbol{H}^{(l)}\)是\(l^{th}\)層的輸出，\((l+1)^{th}\)層的輸入。\(\odot\)是逐元素乘。

這樣，HGCN分別計算兩個KG的embeddings，並在訓練中仍然使用上面所提到過的的alignment score function \(f_{\text{align}}(e_1, e_2)\)+間隔損失函數。

Stage 2

基於關係謂詞的頭實體和尾實體的表徵來獲得其embeddings。該階段先分別計算所有連線關係謂詞的頭實體和尾實體的平均embeddings，接著這兩個均值embeddings會在一個線性變換之後拼接起來做為關係的embeddings，這樣就可以對跨知識圖譜的關係進行對齊。

Stage 3

再次使用Highway-GCN（其輸入為Stage 1中得到的embeddings和與該實體有關的關係謂詞embeddings之和的拼接）做為共同的實體embeddings，然後alignment模組再次使用alignment score function + 間隔損失將兩個知識圖譜在Highway-GCN的輸出對映到統一的向量空間。

2.3 GMNN

GMNN^[4]將實體對齊問題形式化了為兩個圖之間做匹配的問題。傳統的圖匹配問題會通過對單語言知識圖譜的事實進行編碼，將每個知識圖譜的實體投影到低維子空間。然而，對於跨語言問題，一些實體在不同的語言中可能存在不同的知識圖譜事實，這可能導致其在在跨語言的實體embeddings中編碼的資訊具有差異性，從而使得這類方法難以對實體進行匹配。

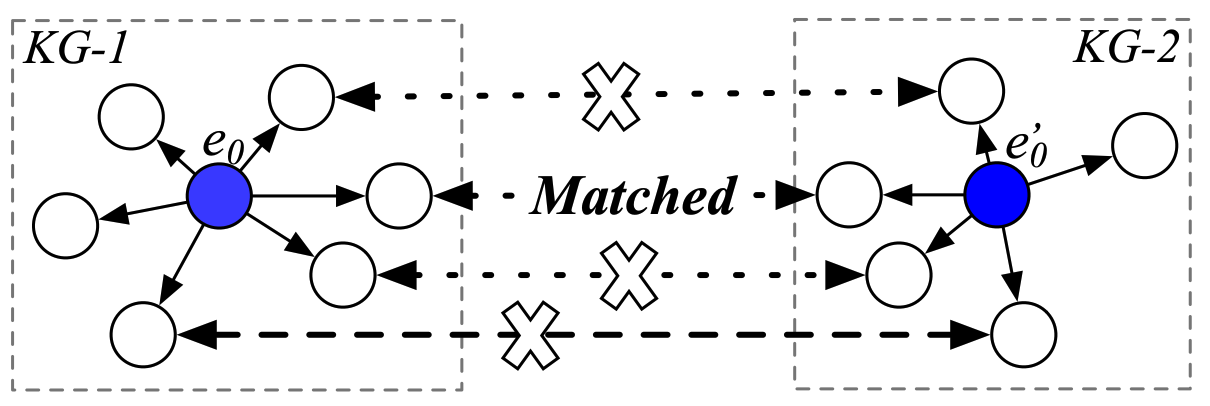
如上圖展示了我們對\(e_0\)和\(e_0'\)進行對齊的範例。但是在它們周圍的鄰居中只有一個對齊的鄰居。這種方法得匹配只有很少的鄰居的實體非常困難，因為缺乏足夠的結構化資訊。

為了解決這個缺點，作者提出了topic entity graph（主題實體圖）來表徵知識圖譜中實體的上下文資訊。不同於之前的方法使用實體embeddings來匹配實體，作者將這個任務建模為在topic entity graph之間進行圖匹配。每個實體都對應一個topic entity graph（由相隔一跳的鄰居和對應的關係謂片語成），這樣的一個圖能夠表徵實體的區域性上下文資訊。

該論文提出的由四層組成，包括輸入表示層、node-level匹配層，graph-level匹配層和預測層。如下圖所示：

輸入表示層使用GCN將兩個topic graph進行編碼並獲得實體的embeddings。

node-level匹配層計算來自兩個topic graph的實體對之間的餘弦相似度。之後，這一層會計算實體embeddings的注意力加權和(attentive sum)：

\[\overline{\boldsymbol{e}}_i=\frac{\sum_{j=1}^{\left|\mathcal{E}_2\right|} \alpha_{i, j} \cdot \boldsymbol{e}_j}{\sum_{j=1}^{\left|\mathcal{E}_2\right|} \alpha_{i, j}}\]

這裡\(\alpha_{i,j}\)是某個topic graph中的實體\(i\)和另一個topic graph中的實體\(j\)之間的餘弦相似度。接著，我們使用multi-perspective sine matching function\(f_m\)來計算\(\mathcal{G}_1\)和\(\mathcal{G}_2\)所有實體的匹配向量，如下式所示：

\[\begin{aligned} &\boldsymbol{m}_i^{\text {att }}=f_m\left(\boldsymbol{e}_i^1, \overline{\boldsymbol{e}}_i^1\right) \\ &\boldsymbol{m}_j^{\text {att }}=f_m\left(\boldsymbol{e}_j^2, \overline{\boldsymbol{e}}_j^2\right) \end{aligned} \]

這裡\(\bm{m} =f_m(\bm{v}_1, \bm{v}_2; \bm{W})\)，其中\(\bm{m}_k \in \bm{m}\)是來自\(k\)個perspective的matching value，它根據兩個向量線性變換後的餘弦相似度進行計算：

\[m_k=\operatorname{cosine}\left(W_k \circ \boldsymbol{v}_1, W_k \circ \boldsymbol{v}_2\right) \]

之後，這個計算好的匹配向量會做為graph-level匹配層GCN的輸入。graph-level匹配層的GCN會進一步傳播區域性的資訊，而其輸出embeddings會經過逐元素最大和平均池化方法被送入一個全連線神經網路來獲得圖的匹配表徵。最後預測層將圖的匹配表徵作為softmax迴歸函數的輸入來預測對齊實體。

2.4 MuGNN

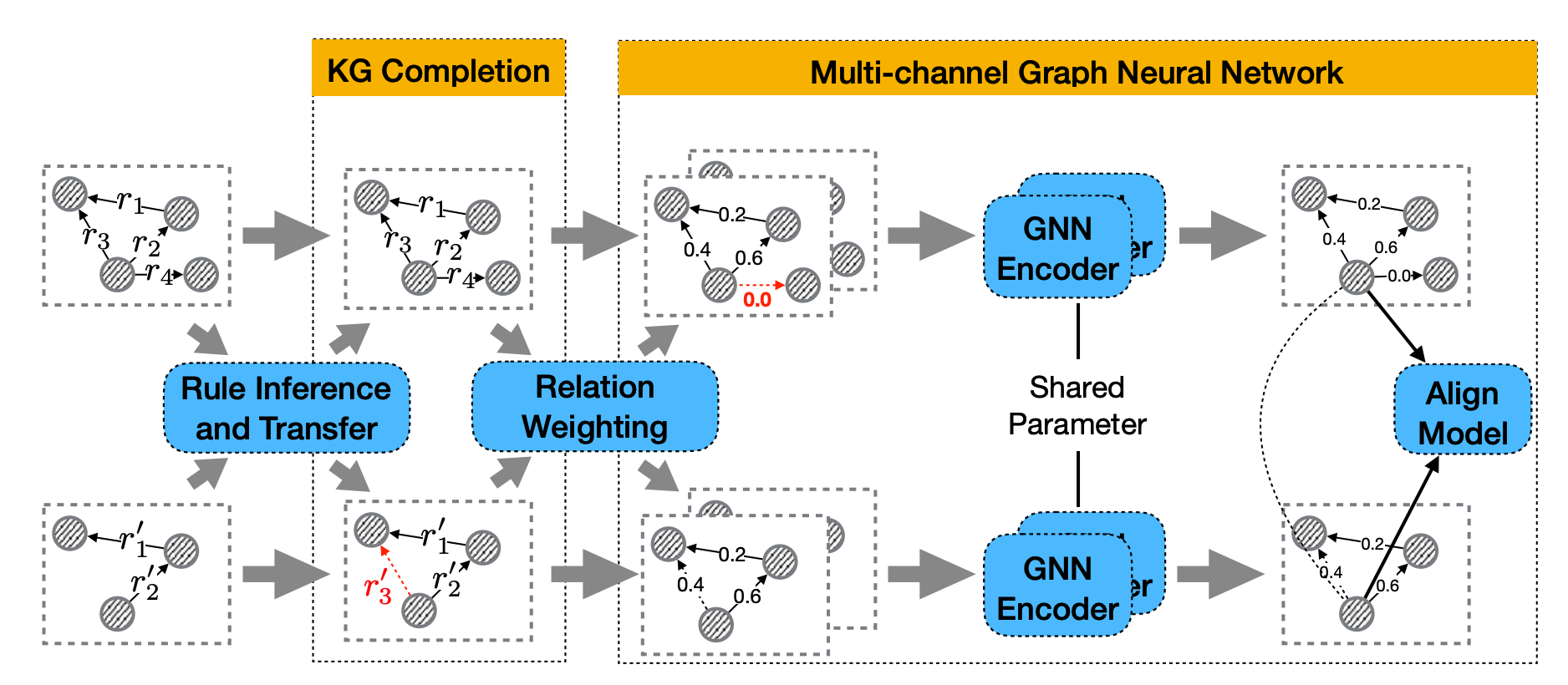
MuGNN^[5]強呼叫於對齊的不同知識圖譜之間的結構異質性，因為這種結構異質性會導致需要對齊實體embeddings之間的不相似性。為了調和\(\mathcal{G}_1\)和\(\mathcal{G}_2\)之間的結構異質性，MuGNN在嵌入模組中使用多通道GNN以編碼多通道圖。形式化地，多通道GNN如下圖所示，假定這裡為雙連結MuGNN：

\[\begin{aligned} &\operatorname{MuLTIGNN}\left(\boldsymbol{H}^l ; \boldsymbol{A}_1, \boldsymbol{A}_2\right)=\operatorname{POOLING}\left(\boldsymbol{H}_1^{l+1}, \boldsymbol{H}_2^{l+1}\right) \\ & \boldsymbol{H}_i^{l+1}=\operatorname{GCN}\left(\boldsymbol{A}_i, \boldsymbol{H}^l, \boldsymbol{W}_i\right), i=1,2 \end{aligned} \]

這裡\(\boldsymbol{A}_1\)由self-attention決定，\(a_{ij}\)是從\(e_i\)到\(e_j\)的連線權值，如下所示：

\[a_{i j}=\operatorname{softmax}\left(c_{i j}\right)=\frac{\exp \left(c_{i j}\right)}{\sum_{e_k \in N_{e_i} \cup\left\{e_i\right\}} \exp \left(c_{i k}\right)} \]

\(N_{e_i}\)是\(e_i\)的鄰居，\(c_{ij}\)是attention係數。

而\(\bm{A}_2\)通過降低互斥（exclusive）實體之間的連線權值來對互斥實體進行修剪。

\[a_{i j} \in \boldsymbol{A}_2=\max _{r_1 \in \mathcal{R}_1, r_2 \in \mathcal{R}_2} \mathbf{1}\left(\left(e_i, r_1, e_j\right) \in \mathcal{T}_1\right) \operatorname{sim}\left(r_1, r_2\right) \]

這裡\(\mathcal{R}_1\)和\(\mathcal{R}_2\)分別是\(\mathcal{G}_1\)和\(\mathcal{G}_2\)關係謂詞的集合。當\(\left(e_i, r_1, e_j\right) \in \mathcal{T}_1\)時函數\(\mathbf{1}(\cdot)=1\)，否則為0。函數\(\operatorname{sim}\left(r_1, r_2\right)\)為關係謂詞\(r_1\)和\(r_2\)之間的內積相似度。

之後MuGNN的alignment模組採用了普通alignment score function的變種將來自多通道GNN的\(\mathcal{G}_1\)和\(\mathcal{G}_2\)的embeddings統一到相同的向量空間，該變種採用了種子實體對齊損失和種子關係謂詞對齊損失的加權和。

改論文的框架整體架構如下：

2.5 NMN

NMN^[6]也旨在解決不同知識圖譜間的結構異質性。為了解決這個問題，該論文采用的方法同時學習了知識圖譜的結構資訊和鄰居的差異，這樣不同實體間的相似性就能夠在結構異質性的情況下被捕捉。

為了學習知識圖譜的結構資訊，NMN的嵌入模組使用我們前面提到過的帶有highway gates的GCN來對知識圖譜的結構資訊進行建模，其中將待對齊的\(\mathcal{G}_1\)和\(\mathcal{G}_2\)做為輸入。這個模型使用種子對齊實體+基於間隔的損失函數進行預訓練。之後，再使用跨圖匹配來捕捉鄰居的差異。之後，NMN將實體embeddings和鄰居表示進行拼接以獲得最終用於對齊的embeddings，其對齊操作是通過度量兩個實體embeddings之間的歐幾里得距離來完成。

該論文所提出方法的框架示意圖如下所示：

2.6 CEA

CEA^[7]考慮實體之間對齊決策的依賴性。比如一個實體如果已經被對齊到某個實體，那麼它就不太可能再被做為對齊目標使用。該網路使用結構化、語意和字串訊號來捕捉源知識圖譜和目標知識圖譜實體之間在不同方面的相似度，而這由三個不同的相似度矩陣來表徵。特別地，這裡的結構化相似度矩陣會經由GCN並使用使用餘弦相似度來計算，語意相似度矩陣由單詞的embeddings來計算，字串相似度矩陣由實體名稱之間的Levenshtein距離計算。這三個矩陣之後會融合為一個矩陣。CEA之後會將實體嵌入形式化為一個在融合矩陣上的經典穩定匹配問題來捕捉相互依賴的EA決策。

3 參考文獻

[1] Zhang R, Trisedya B D, Li M, et al. A benchmark and comprehensive survey on knowledge graph entity alignment via representation learning[J]. The VLDB Journal, 2022: 1-26

[2] Wang Z, Lv Q, Lan X, et al. Cross-lingual knowledge graph alignment via graph convolutional networks[C]//Proceedings of the 2018 conference on empirical methods in natural language processing. 2018: 349-357.

[3] Wu Y, Liu X, Feng Y, Wang Z, Zhao D (2019b) Jointly learning entity and relation representations for entity alignment. In: EMNLP 2019

[4] Cross-lingual knowledge graph alignment via graph matching neural network. In: ACL 2019

[5] Cao Y, Liu Z, Li C, Liu Z, Li J, Chua TS (2019) Multi-channel graph neural network for entity alignment. In: ACL 2019

[6] Wu Y, Liu X, Feng Y, Wang Z, Zhao D (2020) Neigh-borhood matching network for entity alignment. In: ACL 2020

[7] Zeng W, Zhao X, Tang J, Lin X (2020) Collective entity alignment via adaptive features. In: ICDE 2020