BLS簽名演演算法
前言
[失蹤人口迴歸 (*/ω\*)] 真的好久好久沒有更新了,因為自己也還在找方向,但還是把新學的知識記錄在部落格里。今天要介紹的是BLS簽名演演算法。
一、BLS簽名演演算法簡介
BLS簽名演演算法[1]是由斯坦福大學的 Dan Boneh、Ben Lynn 和 Hovav Shacham一同提出的。
一般將 ECDSA簽名演演算法、Schnorr簽名演演算法和BLS進行對比。
ECDSA簽名演演算法侷限性:
無法進行簽名聚合和金鑰聚合。換句話說,當我們驗證多重簽名交易的時候,我們只能逐個對簽名進行驗證,顯然這會耗費大量的區塊空間和交易費。因此並不適用於多重簽名場景。
Schnorr簽名演演算法:
可以將一筆交易中的所有簽名和公鑰合併成單個簽名和公鑰,其過程是不可見的(即無法判斷該簽名或公鑰是否通過合併得到的)。這樣就可以實現只需要一次就可以對合並後的簽名做驗證,加快了區塊驗證的速度。
但其仍然存在著侷限性:
- 多重簽名需要多次(簽名者之間的)通訊,這對冷錢包來說過於麻煩;
- 聚合簽名演演算法依賴亂數生成器,而不像 ECDSA 那樣可以使用指定的隨機點(R);
- m-n 多重簽名機制比較取巧,需要構建公鑰的默克爾樹。當 m 和 n 較大時,樹所佔空間會相當大;
- 無法把一個區塊中的所有簽名聚合成一個簽名。
與這兩個簽名演演算法作比較,BLS有如下優點:
(1)不需要亂數生成器,可以將區塊中的所有簽名聚合成一個;
(2)容易實現 m-n 多重簽名,也可以避免簽名者之間的多餘通訊;
(3)簽名的長度更短(簽名為橢圓曲線上的一個點而非兩個),是 Schnorr 或 ECDSA 的 2 分之一。
二、基礎知識
在對BLS演演算法進行闡述之前,首先了解一下曲線雜湊和曲線配對。
2.1 曲線雜湊
Hashing to the curve 一般可以翻譯為曲線雜湊或者是雜湊成曲線上的點。沒了解之前聽到曲線雜湊可能會不知道是啥,但聽到雜湊成曲線上的點就大概知道意思了。
在一般的雜湊計算中,常常是對於不定長的輸入最終輸出一個定長的數值。但曲線雜湊就不一樣,其輸出結果會對應到橢圓曲線上的一個點。
具體做法如下:
雜湊函數保持不變,將得到的雜湊值作為點的 x 值尋找橢圓曲線上的對應點。
通常來說(比如位元幣所用的曲線),橢圓曲線有 2256 個點,而 SHA-256 雜湊演演算法的值是 256 位。不過,一個有效的 x 座標,會對應一正一負兩個 y 座標(因為(x, y)和(x, -y)都是曲線y²=x³+ax+b上的點)。換句話說,新的雜湊演演算法大約有 50% 的概率在曲線上找到 2 個對應點,另 50% 的概率則一個點也找不到。因此,在應用過程中會出現需要嘗試多次才能找到對應點的情況。
· 有兩個對應點怎麼解決呢?
選擇y座標較小的作為結果即可。
· 那出現找不到對應點的情況怎麼辦呢?
可以在訊息體後面附加一個數。當找不到對應點的時候,將該數加一再重新計算直到找到對應的點。
下面給出一個例子。
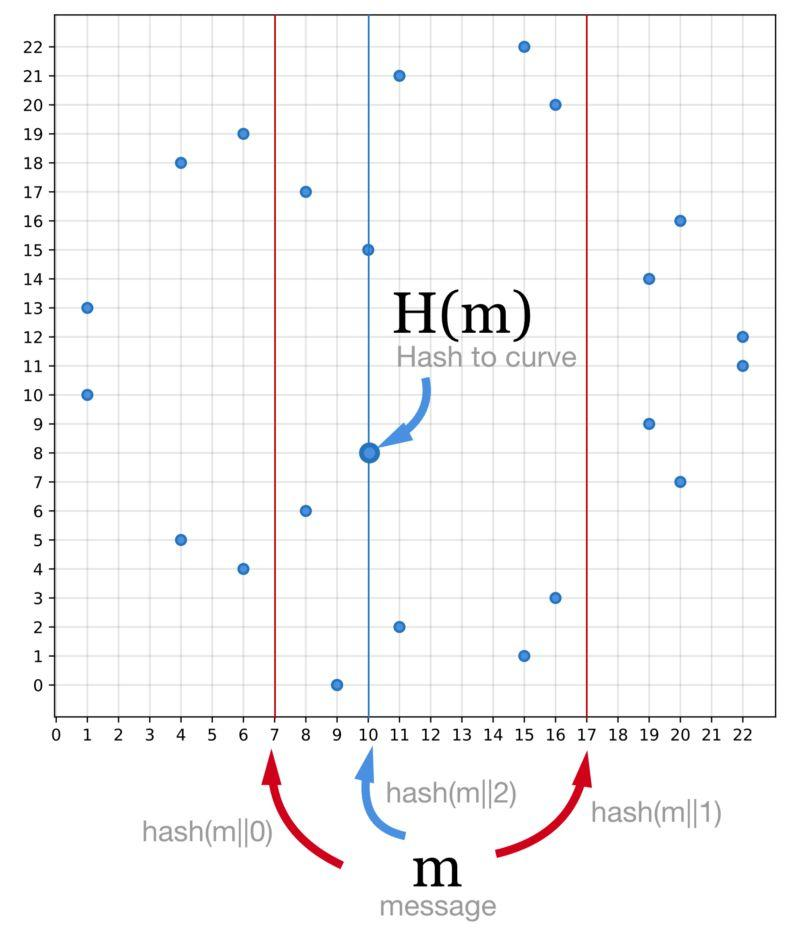
以在模為 23 的有限域上定義的橢圓曲線 y²=x³+7為例。只有一半的 x 座標在曲線上能找到對應點。
① 計算 hash(m||0),沒有對應的點。
② 計算 hash(m||1),沒有對應的點。
③ 計算 hash(m||2),發現對應的點。對應的點有兩個,選擇y座標較小的作為結果。
和 Schnorr 一樣,我們也需要杜絕偽造金鑰攻擊。一種方法是要求每個簽名參與者證明它擁有公鑰對應的私鑰(用私鑰給公鑰簽名)。另一種方法是加入非線性係數,使得攻擊無法實施。要做到這一點,聚合不再是簡單的將多個金鑰和簽名相加,而是將它們分別乘以某個係數後再相加:
S = a1 × S1 + a2 × S2 + a3 × S3
P = a1 × P1 + a2 × P2 + a3 × P3
公式中籤名和金鑰的係數,可以通過簽名者以及其它所有人的公鑰計算得出,公式如下:
ai = hash (Pi, {P1, P2, P3})
舉個例子,可以簡單的將簽名者的公鑰和所有人公鑰拼接在一起算出係數:
ai = hash (Pi || P1|| P2 || P3)
此時,上面的驗證公式依然成立。雖然多了係數ai,但計算邏輯未變。
該方案的好處是,無需在裝置間進行多輪通訊,只需知曉其它簽名者的相應資訊即可。它可比 Schnorr 演演算法(需要 3 輪通訊)的多重簽名方案簡單多了。這個方案也不依賴隨機性,是一種具有完全確定性的簽名演演算法。
4.2 m-n多重簽名
上面對n-n多重簽名進行了介紹,但實際中其實並不是很常見,更常用的是m-n多重簽名。
Schnorr 簽名演演算法中,我們用公鑰組成的默克爾樹來實現金鑰聚合,這種方式效率不高,但是將將堪用。不幸地是,當 m 和 n 的值變大時,默克爾樹的大小會呈指數增長。
BLS 使用了另一種方法,不過略複雜。我們需要一個普通雜湊函數hash(x)(結果為一個數)和一個曲線雜湊函數H(x)。開始多重簽名時,還需要一個初始化過程,這之後,簽名者之間就不再需要通訊了,只需提供交易簽名即可。
下面舉個例子,我們要建立一個 2-3 多重簽名,3 個簽名儲存在不同的裝置上(這個例子可以擴充套件為任意的 m-n 多重簽名)。
(1)生成成員金鑰
用 i = 1,2,3 來表示集合中相應位置的裝置,用pki表示私鑰,用Pi = pki×G表示公鑰。我們用前面說的方法來聚合公鑰:
P = a1 × P1 + a2 × P2 + a3 × P3
其中,ai = hash (Pi, {P1, P2, P3}) .
現在,每個裝置都需要對每個i簽名,以證明該i是聚合公鑰中的一員。將簽名聚合後,儲存在對應的裝置中:
MKi = (a1 × pk1) × H( P , i ) + (a2 × pk2) × H( P , i ) + (a3 × pk3) × H( P , i )
這個簽名被稱作「成員金鑰」,稍後簽名時我們會用到。每個成員金鑰都是對訊息體H( P , i ) 的 n-n 多重簽名,即:
e (G, MKi) = e (P, H(P , i) )
證明如下:

記住這個等式,稍後還會用到。它用來證明某個裝置是多重簽名中的合法參與者。
(2)簽名
假設現在用pk1和 pk3對交易進行簽名,會生成兩個簽名S1和S3:
S1 = pk1 × H(P,m) + MK1
S3 = pk3 × H(P,m) + MK3
將它們加起來,聚合成單一的簽名和公鑰:
(S', P') = (S1+S3, P1+P3)
用P'和S', 是為了強調它們只是由部分簽名者參與計算的(公鑰和簽名),而不像 P 那樣是由所有簽名者參與計算的(公鑰)。為了驗證 2-3 多重簽名,需證明如下等式成立:
e(G,S') = e(P',H(P,m)) × e(P,H(P,1)+H(P,3))
上面說過,成員金鑰 MK1 和 MK3 是對訊息 H(P,1) 和 H(P,3)(訊息本身由聚合公鑰P簽名)的簽名,所以有:
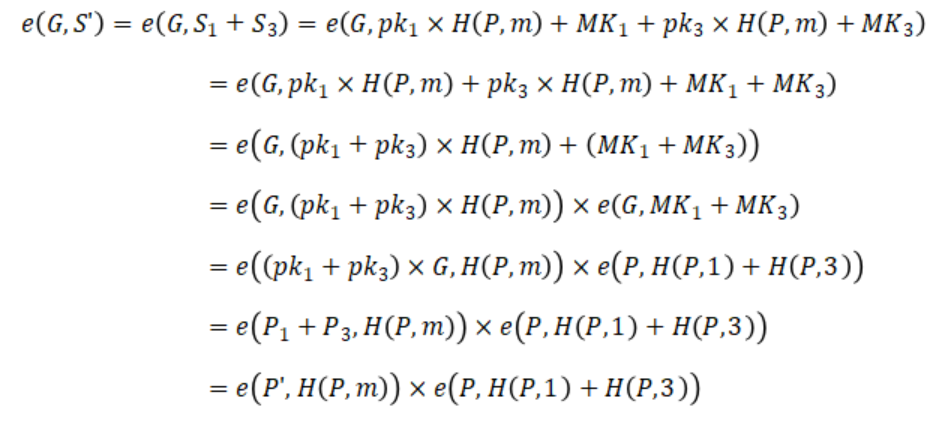
證明完畢。比 n-n 多重簽名複雜一些,但仍然可以理解。
五、缺點
① 配對函數並不是十分高效
② 存在一種針對橢圓曲線加密體系的攻擊-MOV攻擊。該攻擊能夠利用配對函數來危害系統安全。所以對配對函數的使用要十分謹慎。
參考文獻
[1] Boneh D , Lynn B , Shacham H . Short Signatures from the Weil Pairing[J]. Springer, Berlin, Heidelberg, 2001.
[2] 理解 BLS 簽名演演算法