C++ 棧和迷宮問題

1. 前言

棧是一種受限的資料結構，要求在儲存資料時遵循先進後出（Last In First Out）的原則。可以把棧看成只有一個口子的桶子，進和出都是走的這個口子（也稱為棧頂），封閉的另一端稱為棧底。

什麼時候會用到棧？

現實世界裡，類似於棧的儲存現象很普通。

當我們需要同時儲存經常和不經常使用的物品時，我們總是把不經常使用的物品先放到箱子的最裡層，把經常使用的物品放到箱子的最外層。這是典型的棧儲存思想。

在程式設計的世界裡，可把稍後要用的資料儲存在棧底，把當前需要用的資料儲存在棧頂。或者說，如果資料A依賴資料B，也就是必須先處理完B後才能處理A。可以把資料B儲存在棧頂，資料A儲存在棧底。

棧的抽象資料型別：

棧最基本的操作是入棧、出棧，除此之外，還有檢視棧頂、檢查棧是為空、檢查棧已滿……操作。

棧有 2 種實現方案：

順序儲存。
鏈式儲存。

2. 順序儲存

順序儲存指使用陣列模擬棧實現。

2.1 初始化棧

陣列是開放式的資料儲存結構，為了保證向陣列中儲存資料時，遵循棧的儲存理念，棧類需要做 2 點準備：

對外隱藏陣列(私有化)。
棧內部確定儲存位置。入口（棧頂）位置可以從陣列的首地址開始，也可以從陣列的尾地址開始。

template <typename T>
class Stack {
	private:
		//陣列地址（這裡使用動態建立陣列）
		int *items;
		//用來控制陣列中的有效儲存位置（位置控制指標）
		int *index;
		//棧的實際資料的大小
		int size=0;
	public:
		//建構函式
		Stack(int stackSize) {
			this->items=new T[stackSize];
			this->size=stackSize;
             //從陣列的首地址開始儲存
             this->index=this->items;
		}
		//入棧
		void push(T data);
		//出棧
		T pop();
		//檢視棧頂資料
		T getTop();
		//是否為空
		bool isEmpty();
		//是否滿了
		bool isFill();
};

2.2 棧的狀態

棧有 2 種狀態：

可用：入棧時，棧中有空位置，出棧時，棧中有資料，此時棧為可用狀態。
不可用：出棧時，如果棧為空，或入棧時，棧已滿，此時棧為不可用狀態。

為了保證入棧和出棧能正常工作，先要實現狀態檢查函數。

2.2.1 是否為空

這個演演算法很簡單，只需要檢查位置控制指標是不是為構建棧時的最初狀態。

//是否為空
bool isEmpty() {
    return this->items==this->index;
}

2.2.2 是否已滿

只需要檢查棧的大小是否和陣列的實際儲存大小相等。或者檢查位置控制指標是否已經到達陣列尾部。

//是否滿了
bool isFill(){
    return this->index-this->items==this->size;
}

2.3 入棧和出棧

2.3.1 入棧

入棧操作需要檢查棧是否有空位置。如果有，儲存在位置控制指標所指向位置，然後讓位置控制指標指向下一個可用位置。

//入棧
bool push(T data) {
    if(this->isFill()) {
        //棧滿了，不能儲存
        return 0;
    }
    //儲存至位置控制指標所指位置 
    *(this->index)=data;
    //移動 
    this->index++;
    this->size++;
    return 1;
}

2.3.2 出棧

出棧時需要檢查棧是否為空，為空時，出棧失敗。不為空時，把位置控制指標向後移動到資料所在位置，然後得出資料。

//出棧
T pop() {
    if(this->isEmpty()) {
        //棧為空
        return NULL;
    }
    this->index--;
    this->size--;
    return *(this->index);
}

2.3.3 其它函數

返回棧中實際資料的函數。

//得到棧中的實際資料大小
int getSize(){
    return this->index-this->items;
}

僅查詢棧頂資料，不從棧中刪除資料。

//檢視棧頂資料
T getTop() {
    if(this->isEmpty()) {
        return NULL;
    }
    return *(this->index-1);
}

2.3.4 測試入棧出棧

棧儲存會導致存入的順序和輸出的順序是相反的。

int main(int argc, char** argv) {
    Stack<int> myStack(10);
    //向棧中壓入資料
    for(int i=0; i<15; i++) {
        myStack.push(i);
    }
    int top=myStack.getTop();
    cout<<"棧頂資料："<<top<<endl;
    int size=myStack.getSize();
    cout<<"棧中資料的大小:"<<size<<endl;
    cout<<"輸出棧中所有資料："<<endl;
    for(int i=0; i<15; i++) {
        cout<<myStack.pop()<<endl;
    }
    return 0;
}

輸出結果：

向棧中新增了 15 次資料，因棧的容量只有 10，最終輸出只有 10 個有效資料。最後的 5 個 0 表示出棧失敗。

2.4 小結

因順序棧基於陣列，實現過程相對而言較簡單，但受限於陣列的物理特性，在壓入的資料多於棧內部大小時，會出現資料溢位問題。雖然可以採用擴容演演算法，但同時增加了程式碼的維護量。

3. 鏈式儲存

鏈式儲存是基於結點的儲存方式，資料在物理結構上是不連續的。連結串列儲存的優點是可以自行動態擴容，不需要演演算法層面的支援。

鏈式儲存的流程：

3.1 結點型別

結點型別和單連結串列相同，只需要資料域和儲存下一個結點的指標域。

template <typename T>
class Node {
	public:
		T data;
		Node *next;
		Node(T data) {
			this->data=data;
			this->next=NULL;
		}
};

3.2 初始化

建立連結串列時，通常會增加一個空白頭結點作為標誌結點，在構建連結串列棧時是不需要的。

template <typename T>
class Stack {
	private:
		//頭結點指標
		Node *head; 
		//棧中實際資料的大小
		int size;
	public:
		//建構函式
		Stack() {
            //不需要空白頭結點
			this->head=NULL;
             this->size=0;
		}
		//入棧
		bool push(T data)  ;
		//出棧
		T pop() ;
		//檢視棧頂資料
		T getTop() ;
		//得到棧中的實際資料大小
		int getSize(){
            return this->size;
        }
};

3.3 入棧、出棧

連結串列的資料插入方案有頭部插入和尾部插入兩種方案。在模擬棧時須保證資料的維護只能在一端進行，可以有 2 種方案：

資料的插入和刪除在頭部進行。
資料的插入和刪除在尾部進行。

本文以頭部插入實現入棧和出棧演演算法。

3.3.1 入棧

鏈式棧不需要考慮棧是已經滿的問題。入棧實現流程：

建立一個新結點物件。
原來的頭結點成為新結點的後驅結點。
新結點成為頭結點。

//入棧
bool push(T data) {
    //建立新結點
    Node<T> *newNode=new Node<T>(data);
    if(newNode){
        //原來的頭結點成為新結點的後驅
        newNode->next=this->head;
        //新結點成為頭結點
        this->head=newNode; 
        this->size++;
        return 1;
    }else{
        return 0;
    }
}

3.3.2 出棧

鏈式棧的出棧操作需要判斷棧是否為空。如果不為空剛取出頭結點資料，並把結點從連結串列中刪除。實現流程：

//出棧
T pop() {
    Node<T> * node=NULL; 
    T data; 
    if(this->head){
        //獲取頭結點
        node=this->head;
        //得到資料
        data=node->data;
        //原來頭結點的後驅成為新頭結點 
        this->head=this->head->next; 
        //刪除結點
        delete node;
        this->size--;
        return data; 
    }else{
        //連結串列為空 
        return NULL;
    }
}

為了方便查詢棧頂資料，需要提供一個查詢棧頂資料的操作。

//檢視棧頂資料
T getTop() {
    if(this->head) {
        return this->head->data;
    } else {
        return NULL;
    }
}

3.3.3 測試鏈式棧

int main(int argc, char** argv) {
	Stack<int> stack ;
	//入棧
	for(int i=0; i<10; i++) {
		stack.push(i);
	}
	cout<<"棧中實際資料大小："<<stack.getSize()<<endl;
	cout<<"查詢棧頂資料:"<<stack.getTop()<<endl;
	//出棧
	for(int i=0; i<10; i++) {
		cout<<stack.pop()<<endl;
	}
	return 0;
}

執行結果：

4. STL 中的棧

實際應用時，可以使用STL的stack容器。除了上述的基本操作外，stack容器還提供比較操作，這些操作可以被用於棧與棧之間的比較，相等指棧有相同的元素並有著相同的順序。

#include <iostream>
#include <stack>
using namespace std;
int main(int argc, char** argv) {
	stack<int> myStack;
	//入棧 
	for(int i=0;i<5;i++){
		myStack.push(i);
	}
	cout<<"棧中資料大小:"<<myStack.size()<<endl;
	 
	//出棧 
	for(int i=0;i<4;i++) {
		cout<<"棧頂資料："<<myStack.top()<<endl;
		myStack.pop();
	}
	
	cout<<"棧頂資料："<<myStack.top()<<endl;
	stack<int> myStack_;
	myStack_.push(0);
	bool res= myStack_==myStack;
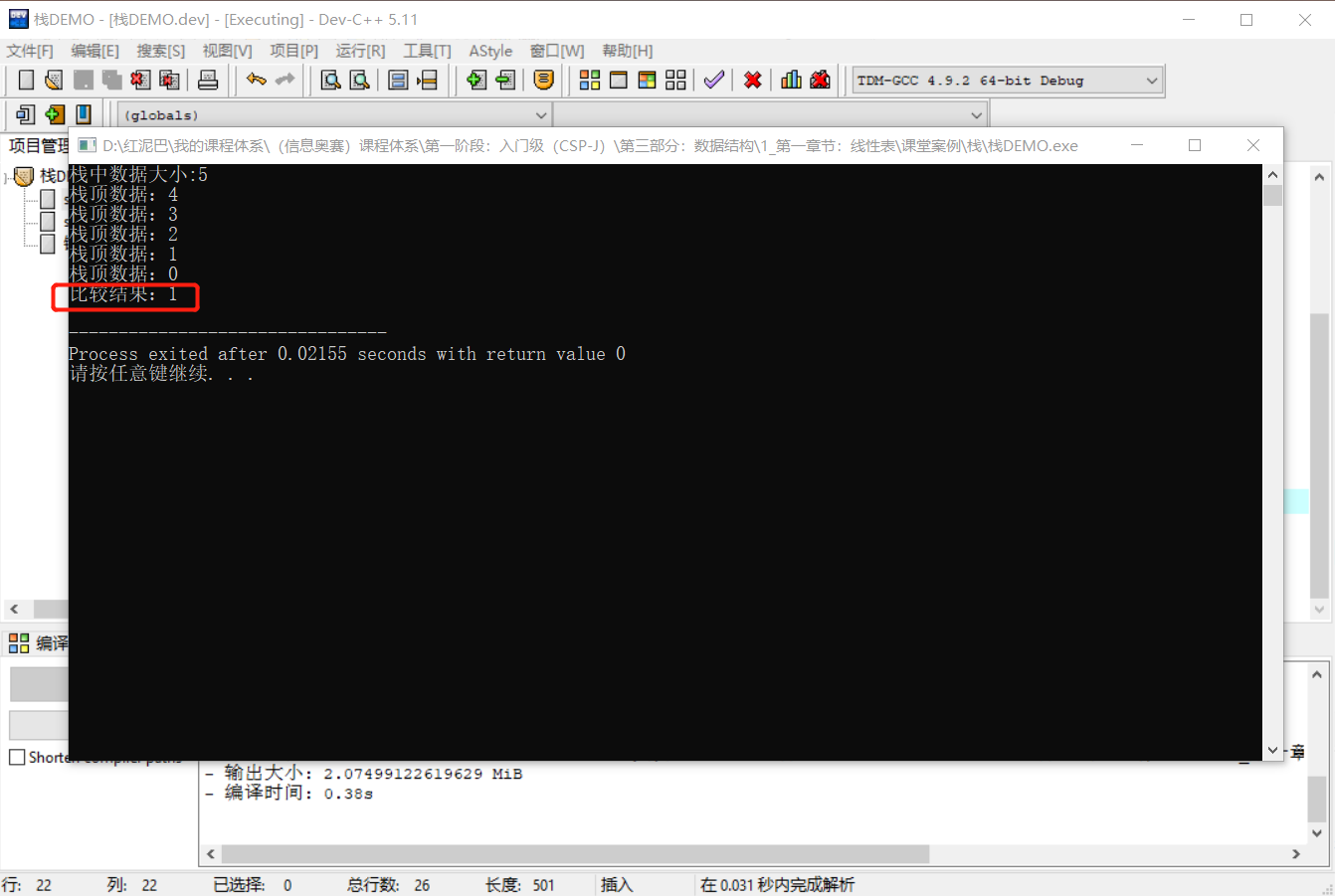
	cout<<"比較結果："<<res<<endl; 
	return 0;
}

輸出結果：

5. 棧的應用

總是在想，如果沒有棧，程式設計將如何進行，可想而知，棧的重要性。函數呼叫、遞迴演演算法……無處不有棧的身影。下面將通過一個典型的案例加深對棧的理解。

5.1 迷宮問題

迷宮問題描述：在一個錯綜複雜的迷宮世界，有一個入口，有一個出口。在入口位置有一隻小老鼠，出口位置有一塊乳酪。要求通過編碼的方式幫助小老鼠在入口到出口之間找到一個可行的路徑。

迷宮問題是一類典型問題，解決此類問題的關鍵思想包括：

試探過程：每到達一個當前位置（第一個當前位置為入口），記錄此當前位置四周可嘗試的其它位置，然後選擇其中一個位置作為當前位置嘗試著繼續前進。

如下表格，設值為0的單元格為可通行，1為不可通行。值標識為紅色的單元格表示當前位置，在繼續前進時，記錄其左、右、下三個可行位置。並選擇右邊位置為新的當前位置。

回溯過程：當在前進時被阻礙後，退到記錄表中下一個可行位置再試。重複試探再回溯至到找到出口。

如上圖所示後繼續選擇右行，則發現被阻礙。

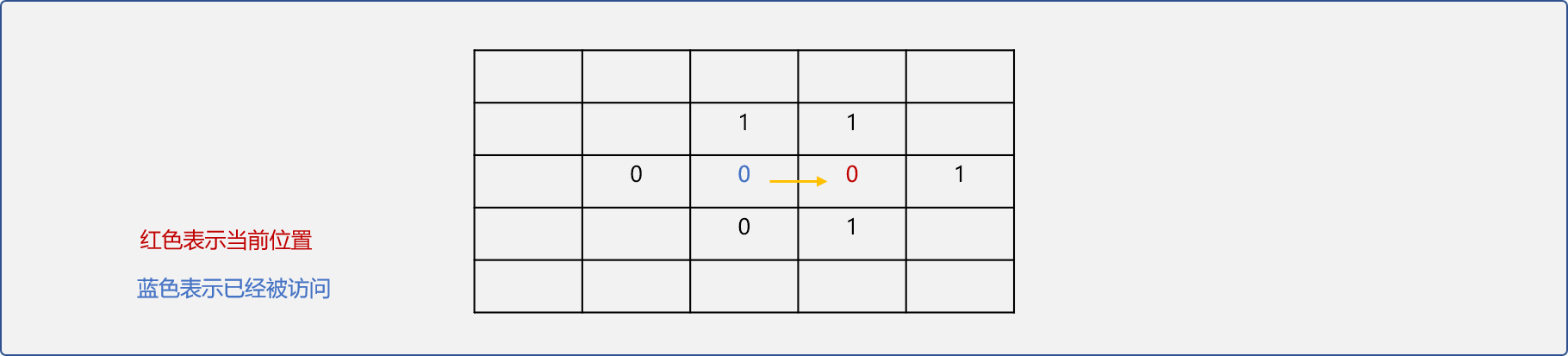
這時就需要在已經儲存的可行位置選擇一個，這步操作稱為回溯。

很明顯，每次記錄的可嘗試位置是在回溯後使用的，符合先進後出的儲存理念。棧在迷宮問題中用來儲存可試探的位置。

實現流程：

使用二維陣列模擬迷宮。在二維陣列中用 0 表示可通行，1 表示不可通行。

#include <iostream>
#include <stack>
#include <vector>
//全域性宣告
int nums[10][10];

初始化迷宮。為了簡化問題，會把二維陣列的第一行和最後一行，第一列和最一列中的所有單元格賦值 1，表示牆面。

如下圖，設定入口位置(1,1)、出口位置為(8,8)。

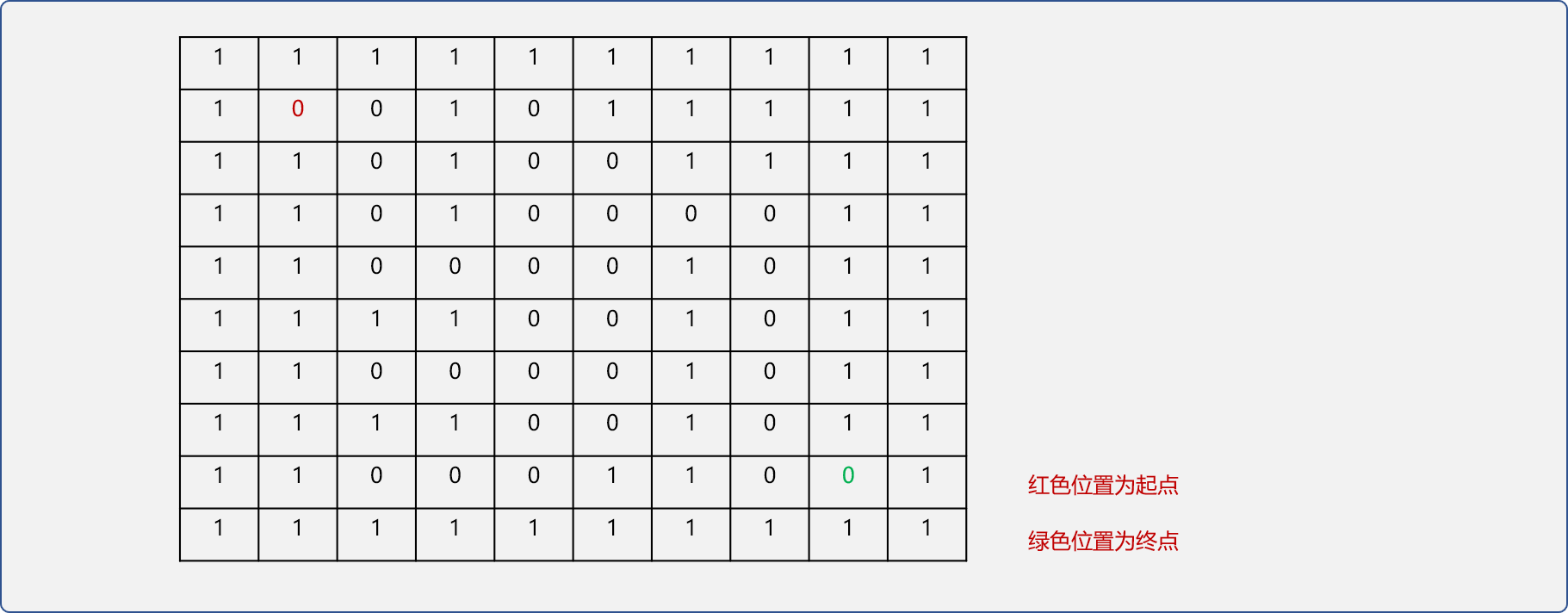
//全域性宣告
int nums[10][10]= {
		{1,1,1,1,1,1,1,1,1,1},
		{1,0,0,1,0,1,1,1,1,1},
		{1,1,0,1,0,0,1,1,1,1},
		{1,1,0,1,0,0,0,0,1,1},
		{1,1,0,0,0,0,1,0,1,1},
		{1,1,1,1,0,0,1,0,1,1},
		{1,1,0,0,0,0,1,0,1,1},
		{1,1,1,1,0,0,1,0,1,1},
		{1,1,0,0,0,1,1,0,0,1},
		{1,1,1,1,1,1,1,1,1,1},
	};

對於二維陣列中的任一位置有左、下、右、上 4 個方向，當前位置的座標與 4個方位的座標關係如下圖所示：

這裡定義一個方向結構體，用來儲存 4 個方位的增量資訊，便於計算。

//方向
struct Direction{
	//x 方向增量 
	int xOffset;
	//y 方向增量
	int yOffset;	
};

並且建立 Direction型別陣列，用於儲存 4 個方向的增量資訊。

//全域性宣告
Direction dirs[4]={ {0,1},{1,0},{0,-1},{-1,0} };

方向資訊，為快速找到當前位置周邊的座標提供了便利。為了儲存座標，這裡需要一個座標結構體：

struct Position {
	//x座標
	int x;
	//y座標
	int y;
    //無參構造
	Position() {

	}
    //有參構造
	Position(int x,int y) {
		this->x=x;
		this->y=y;
	}
    //判斷 2 個座標是不是同一個位置
	bool equals(Position pos) {
		return this->x==pos.x && this->y==pos.y;
	}
    //自我顯示
	void desc() {
		cout<<"x:"<<x<<"y:"<<y<<endl;
	}
};

建立棧。

用來儲存當前位置周邊所有可以通行的位置。

這裡使用 STL提供的stack容器。別忘記包含<stack>標頭檔案。

//全域性宣告
stack<Position> myStack;

核心搜尋演演算法。

所有核心程式碼直接編寫在 main 函數中，下面程式碼中使用到了 vector，儲存已經搜尋到的位置。還有一點要注意，當某個位置被壓入棧中後，要標識為被壓入，這裡把此位置值設定為 -1。

int main(int argc, char** argv) {
	//起點位置
	Position startPos(1,1);
	//終點位置
	Position  endPos(8,8);
	//儲存走過的位置
	vector<Position> paths;
	//向棧中壓入起始位置
	mazeStack.push(startPos);
	//設定起始位置為已經存取過
	maze[startPos.x][startPos.y]=-1;
	//臨時儲存棧頂位置
	Position tmp;

	while(!mazeStack.empty()) {
		//取出棧頂位置
		tmp=mazeStack.top();
		//刪除棧頂資料
		mazeStack.pop();
        //當前搜尋位置儲存在 vector 中
		paths.push_back(tmp);

		//判斷是否已經到了終點
		if (tmp.equals(endPos)) {
			//到達終點，結束
			break;
		} else {
			for(int i=0; i<4; i++) {
				//查詢當前位置 4 個方向有無可通行位置,並壓入棧中
				Position nextPos(tmp.x+dirs[i].xOffset,tmp.y+dirs[i].yOffset);
				if(maze[nextPos.x][nextPos.y]==0) {
					mazeStack.push(nextPos);
                     //標識為已經被壓入，避免重複壓入
					maze[nextPos.x][nextPos.y]=-1;
				}
			}
		}
	}
	
	//顯示搜尋路徑 
	for(int i=0;i<paths.size();i++){
		tmp=paths[i];
		tmp.desc();		
	}
	return 0;
}

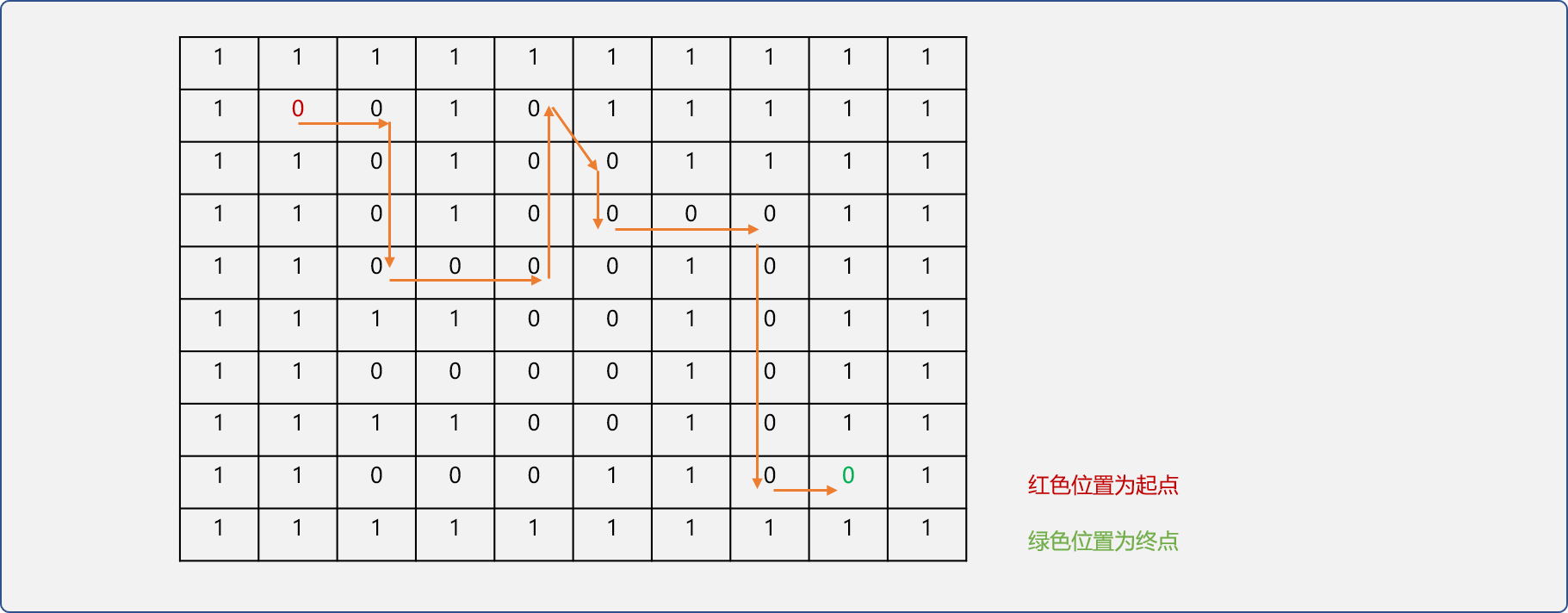
執行結果：

在演示圖中標註出搜尋路徑，可驗證搜尋到的路徑是可行的。

6. 總結

本文編碼實現了順序棧和鏈式棧，簡要介紹了STL中的stack容品，並使用它解決了典型的迷宮問題。

C++ 棧和典型迷宮問題