從零開始學Graph Database:什麼是圖
摘要:本文從零開始引導與大家一起學習圖知識。希望大家可以通過本教學學習如何使用圖資料庫與圖計算引擎。本篇將以華為雲圖引擎服務來輔助大家學習如何使用圖資料庫與圖計算引擎。
本文分享自華為雲社群《從零開始學Graph Database(1)》,作者:弓乙 。
基礎概念
什麼是圖?
首先,我們需要明確圖 Graph的概念。
這裡的圖,是graph, 是graphical,而不是graphic。即圖處理的是關係問題,而不是圖片。我們解決是關係問題,而非視覺cv問題。

在離散資料中,有專門研究圖的圖論。包含子圖相關,染色,路徑,網路流量等問題。
在電腦科學中,我們將圖抽象為一種資料結構,即由點,邊構成的集合。我們可以將現實世界的任意一種包含關係的實體用圖來抽象概括。
我們通常把圖的問題定義為G=(V,E,φ):
V:是節點的集合 E:是邊的集合 φ: E->{(x,y) | (x,y)∈ V^2 ∪ x≠y }是一個關聯函數,它每條邊對映到一個有頂點組成的有序對上。
下圖是一個使用圖來描述的社群網路。點代表了人,邊代表了人和人之間為朋友關係。在構建了這樣一個社群網路以後,我們可以通過使用圖查詢和演演算法使得圖資料產生價值。如利用k跳查詢,共同鄰居,node2vec等來為社群網路中的使用者進行好友推薦。
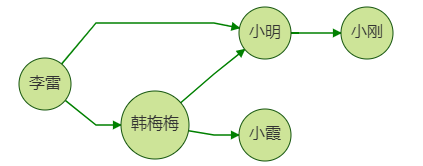
// 好友推薦邏輯 試想我們為李雷推薦好友,思路是:向他推薦其好友的好友。但是需要過濾掉本身李雷的好友。 如上圖,小明即是李雷的好友,也是李雷好友的好友。所以在這種情況中,我們不需要再向李雷推薦小明瞭。 而是推薦 小霞和小剛。 這種稍微有點複雜的推薦思路,可以使用查詢語言進行。 以gremlin為例: g.V("李雷").repeat(out("friend").simplePath().where(without('1hop')).store('1hop')). times(2).path().by("name").limit(100)
可以使用圖做什麼?
傳統上我們使用圖來解決一些數學問題。比如圖論起源於著名的柯尼斯堡七橋問題, 該問題被尤拉推廣為:怎樣判斷是否存在著一個恰好包含了所有邊,且沒有重複的路徑。即一筆畫問題。

尤拉證明了以下定理,並解決了一筆畫問題:
連通的無向圖G有尤拉路徑(一筆畫)的充要條件是:G中的奇點的數目等於0或2。
(奇點:連線邊數為奇數的頂點。)
我們可以用一筆畫問題來解決七橋問題,從模型可以看出來,七橋問題中的奇點數目為4個,顯然不滿足一筆畫的充要條件。故七橋無法在所有橋都只能走一遍的前提下,把這個地方所有的橋都走遍。
當然了,圖並非只能解決這類圖論經典問題(如 四色問題,馬的遍歷問題,郵遞員問題, 網路流問題 ),只要能夠將研究物件表示為圖結構,就能利用圖的特點來解決問題,甚至大部分情況下,並不需要使用到多麼高深的演演算法。
查詢與演演算法
圖查詢
這裡的查詢一般指代使用原生圖查詢語言進行的圖上物件的查詢操作。如neo4j的Cypher,tinkerpop的Gremlin等。Cypher與Gremlin也是業界使用較多的查詢語言,Cypher是側重於pattern matching的宣告式語言,而Gremlin則是基於groovy的函數語言程式設計語言,強調graph traversal的重要性。

如:
1、gremlin
g.V("李雷").outE('friend').has('age',gt(30)).otherV().where(out('friend').(hasId('李雷'))).limit(100)
2、cypher
match (a)-[r1:friend]->(b)-[r2:friend]->(c) where a.mid='李雷' and r1.age>30 and a=c return id(b) limit 100
以上兩種寫法等價,只是使用的圖查詢語言有區別。
圖演演算法
除了明確規則的查詢外,我們也可以利用圖演演算法對圖進行分析。畢竟圖中蘊含的資訊量遠比表面看上去多,這個時候我們希望通過圖演演算法揭示圖中更多的資訊,如發現節點之間隱含關係,分析節點重要性,對業務場景進行行為預測等。
下表列出了目前不同型別具有代表性的圖演演算法:
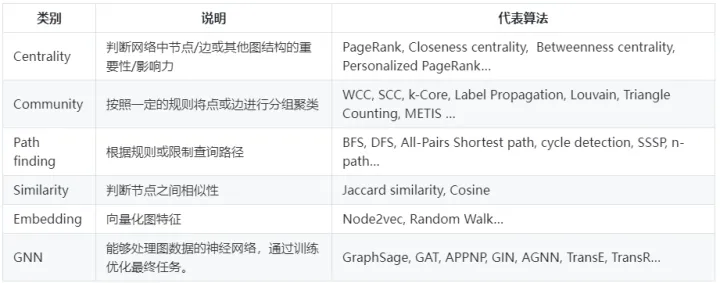
實際的場景中,我們需要同時兼顧演演算法的效果和執行成本。這也是很多使用場景所面臨的trade-off問題。正如我們前面所說,大部分情況下不需要用到非常高深的圖演演算法,特別是在線上任務中,我們更看重時延和效率。

亦或者說,線上場景中,重查詢輕演演算法;而在離線場景中,重演演算法而輕查詢。
事實上,圖查詢與圖演演算法的邊界並沒有那麼涇渭分明。或者說,圖演演算法算是某種程度上的特殊圖查詢。我們普遍認為演演算法較查詢需要更多的計算資源,會佔用更多的CPU與記憶體。

比如上圖的多跳查詢和BFS algorithm,本質上是同一個查詢。灰色模組顯示的是gremlin與cypher的查詢方法,藍色模組顯示的是不同圖資料庫中BFS演演算法的執行方式。但他們的結果都是一致的,均為點Tom的三度鄰居。也就是在業界,N跳查詢即可以作為廣度/深度優先演演算法/khop演演算法單列出來,也可以作為圖遍歷/圖查詢中一種常用模式存在。

除此以外,subgraph matching也是一個圖查詢與圖演演算法同時存在的研究課題。如上圖,我們輸入目標子圖q,在圖G中尋找其同構圖,這其實是一個NP-Hard問題。
當然了,即使子圖查詢是一個非常困難的問題,大部分圖查詢語言還是提供了相應的match語法用於基於模式匹配的搜尋功能,如neo4j使用的Cypher,或者支援指令式和宣告式查詢的Gremlin。而在圖演演算法領域,subgraph matching則是一個極重要,極複雜的研究課題。下表中列出來一部分具有代表性的子圖匹配演演算法的分類。(來源於paper[In-Memory Subgraph Matching: An In-depth Study])。
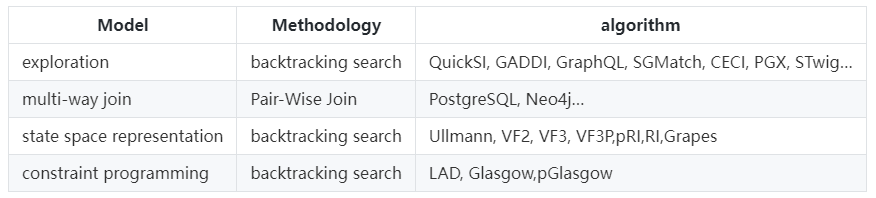
圖的應用
下面讓我們從一個具體的例子中體會一下圖在場景中的使用。
假設我們需要在社交關係中為使用者推薦好友,在不同的場景中,可以使用不同類別的查詢和演演算法。如果用於線上推薦,我們可以將二度鄰居作為其推薦結果,即2跳查詢,這在大部分的圖資料庫中是一個代價非常小的查詢,大多可在100ms以內完成,甚至可以在10ms內返回;如果用於離線推薦,則會傾向於使用推薦效果更優秀的圖演演算法。例如,利用社團演演算法louvain, labelPropagation, Strongly Connected, k-Core獲得每個點的社團分類,並將分類結果作為點上embedding的vector參與後續downstream task計算;或者直接使用圖上Node embedding演演算法(Node2vec, FastRP, Weisfeiler-Lehman等)得到一個完整的點上Embedding的結果用於後續訓練;當然,也可以直接使用圖相似性演演算法(Cosine, Jaccard等)直接得到針對某個點的推薦結果。
gremlin: g.V('李雷').out().out() cypher: match (n)--(m)--(l) where id(n)='李雷' return l louvain: [GES API] POST /ges/v1.0/{project_id}/graphs/{graph_name}/action?action_id=execute-algorithm { "algorithmName": "louvain", "parameters": { "max_iterations": "100", "convergence": "0.01", "weight":"score" } }
大部分的工業使用場景中,圖更多地扮演著資料庫的角色,用來管理某個領域內的關係資料。使用者大多看中圖對於多跳關聯分析能力,以及資料間脈絡的整理歸集,分析和視覺化。
特別的,在某些垂直領域,由於其天生的關係結構,圖資料庫/圖計算已經成為其不可或缺的工具了。如,在金融機構使用圖來進行風控管理,通過對使用者聯絡人交易等資料分析,識別欺詐借貸行為,規避惡意借貸風險,識別黑產群體等;或作為知識圖譜的底層,提供快速關聯查詢,路徑識別推薦,融合各種異構異質資料等。
為了更真實地體驗圖在各個行業的應用,也可以使用以下開箱即用的demo進行動手實踐:
以上案例提供了包括資料來源,資料建模(schema),雲上創圖,查詢或分析演示等功能。