支配樹🌴學習筆記
支配樹:在 \(O(n\log n)\) 時間內求出一張有向圖中能切斷一個點到起點的所有路徑的點
具體地,先定義一個起點 \(S\)(要求它能到達所有點),對於圖中一個點 \(u\),存在一些點 \(v\),使得刪去某個 \(v\) 後 \(S\) 無法走到 \(u\),這些點 \(v\) 所組成的集合就是支配樹上 \(u\) 到根的路徑。特別地,\(u\) 的父親就是離它最近的支配點。
一個很重要的性質:對於任意點 \(u\),如果 \(x\) 支配 \(u\) 且 \(y\) 支配 \(u\),則 \(x\) 與 \(y\) 之間存在支配關係。
證明顯然。由此不難推出支配關係形成一棵樹。
求支配樹的方法:
1. DAG 上求支配樹
按照拓撲序列舉所有點,對於一個點 \(u\),所有能到達它的點的支配樹已經求出, 於是我們列舉 \(u\) 的入點 \(v\),找出它們在已求出的支配樹上的 LCA,即為 \(u\) 的支配點(證明感性理解),然後將 \(u\) 加入支配樹。
注意我們需要「動態」求這個 LCA,這問題不大,我們只需要每找到一個 \(u\) 的父親時就立即更新它的倍增陣列 fa[u][i] 即可。時間複雜度就 \(O(n\log n)\)。
2. 一般圖上求支配樹
我們發現在 DAG 上很好做,考慮將一般圖鼓搗成一個 DAG 且支配關係不變。
用著名的 Tarjan 思想,我們先搜出一棵 dfs 樹再說。立即發現一個點 \(u\) 的支配點一定在它的dfs樹的祖先中。
接下來,引入一個大家初學 Tarjan 就熟知的定理:對於有向圖的 dfs 樹而言,只存在前向邊與反向邊,不存在橫叉邊。
即只有祖先向孫子連邊或孫子向祖先連邊。
同樣 DAG 部分,這次我們按dfs序逆序對每個點 \(u\) 考慮它的所有入點 \(v\),維護一個「半支配點」\(semi_u\)。
分兩種情況:
- \(v\) 為 \(u\) 的祖先。
此時 \(v\) 能一步走到 \(u\),所以從 \(v\) 到 \(u\) 的路徑上所有其它點都不可能成為 \(u\) 的支配點(否則壓根切不斷),所以 \(u\) 的真實支配點應該在 \(v\) 上方,故用 \(v\) 更新 \(u\) 的半支配點。(這裡的更新指取 dfs 序最小的作為答案) - \(v\) 為 \(u\) 的子孫。
此時我們考慮 \(u\) 到 \(v\) 的路徑上所有點 \(w\) 以及它們的半支配點 \(semi_w\),發現如果我們割的點在任意一個 \(semi_w\) 下方,那麼從根就可以走路徑 \(S\rightarrow semi_w\rightarrow w\rightarrow v\rightarrow u\) 到達 \(u\),矛盾。因此用所有 \(w\) 的半支配點 \(semi_w\) 更新 \(u\) 的半支配點 \(semi_u\)。
畫個圖理解一下:
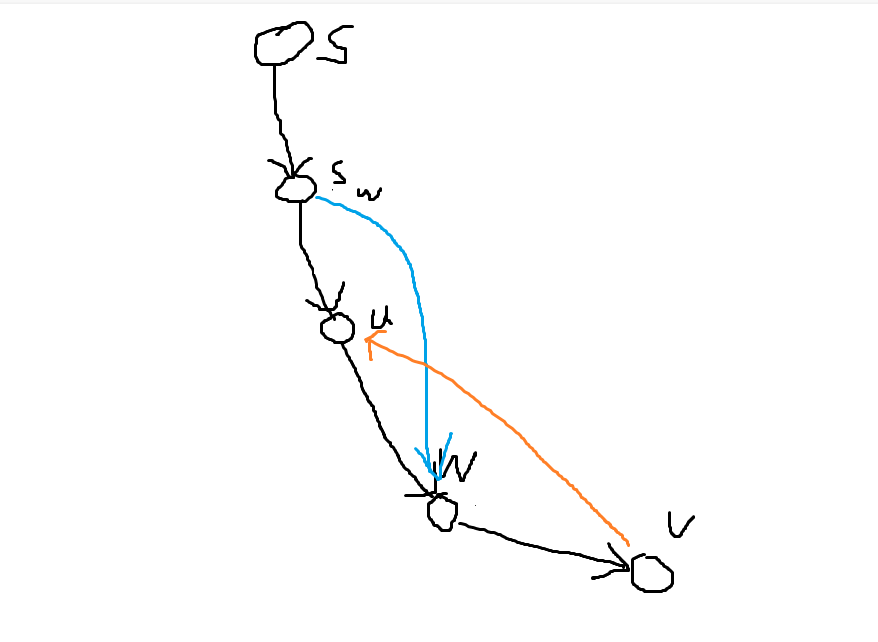
更新完畢後,我們就得到了每個點 \(u\) 的「半支配點」。「半支配點」的本質意義在於,\(u\) 的真實支配點一定在它的半支配點到根的路徑上。因此只保留 dfs 樹上的邊以及新加入的 \(semi_u\rightarrow u\) 的邊,整張圖的支配關係不變。
於是我們只保留原 dfs 樹中的邊,將其它邊統統刪掉,然後對於每個 \(u\) 加入邊 \(semi_u\rightarrow u\),在這個新的只有 \(2(n-1)\) 條邊的 DAG 上跑做法 1 即可。
現在只剩下怎麼快速對一個點 \(v\) 找出 \(u\) 到 \(v\) 的路徑上所有 \(w\) 的 \(semi_w\) 的 dfs 序最小值的問題了。
考慮維護每個點 \(v\) 已存取的祖先中 \(semi\) 的最小值 \(mn_v\),查詢時恰好就是查詢 \(v\) 的 \(mn_v\)(因為 \(v\) 的祖先中第一個未存取的點就是 \(u\))。用並查集維護,每次存取完一個節點 \(u\) 就被其父親 \(fa_u\) 合併即可。時間複雜度 \(O(n\alpha(n))\) 或 \(O(n\log n)\)(我們都懶得寫按秩合併對吧)。
總時間複雜度 \(O(n\log n)\)。
上一個封裝好的程式碼:(注意程式碼中 \(mn_u\) 直接寫成了 semi[u],所以必須在存取完一個 \(u\) 之後立即將其加入新圖中)
#include <bits/stdc++.h>
#define For(i,a,b) for(int i=a;i<=b;i++)
#define Rev(i,a,b) for(int i=a;i>=b;i--)
#define Fin(file) freopen(file,"r",stdin)
#define Fout(file) freopen(file,"w",stdout)
using namespace std;
const int N=2e5+5; typedef long long ll;
class DominatorTree{
int n,dfn[N],raw[N],dfscnt,semi[N],fa[N],pa[N],ffa[N][18],dep[N],in[N];
vector<int> to[N],from[N],cp[N],cv[N];
void dfs(int u){
raw[dfn[u]=++dfscnt]=u; for(int v:to[u]) if(!dfn[v]) { cp[u].push_back(v); pa[v]=u; dfs(v); }
}
int getfa(int x){
if(x!=fa[x]) { int t=getfa(fa[x]); semi[x]=min(semi[x],semi[fa[x]]); fa[x]=t; } return fa[x];
}
int lca(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
Rev(i,17,0) if(dep[ffa[x][i]]>=dep[y]) x=ffa[x][i];
if(x==y) return x;
Rev(i,17,0) if(ffa[x][i]!=ffa[y][i]) { x=ffa[x][i]; y=ffa[y][i]; }
return ffa[x][0];
}
public:
void init(int _n) { n=_n; }
void add_edge(int x,int y) { to[x].push_back(y); from[y].push_back(x); }
void solve(int* ans){
dfs(1); assert(dfscnt==n);
For(i,1,n) { fa[i]=i; semi[i]=dfn[i]; }
Rev(i,n,2){
int u=raw[i]; for(int w:from[u]) { getfa(w); semi[u]=min(semi[u],semi[w]); }
fa[u]=pa[u]; cp[raw[semi[u]]].push_back(u); // Must do it right now!
}
For(u,1,n) for(int v:cp[u]) { cv[v].push_back(u); in[v]++; }
static int q[N],h,t; h=t=0; q[t++]=1;
while(h<t){
int u=q[h++]; ans[u]=0;
for(int v:cv[u]) if(ans[u]==0) ans[u]=v; else ans[u]=lca(ans[u],v);
dep[u]=dep[ffa[u][0]=ans[u]]+1; For(i,1,17) ffa[u][i]=ffa[ffa[u][i-1]][i-1];
for(int v:cp[u]) if((--in[v])==0) q[t++]=v;
}
}
}T;
int n,m,ans[N],siz[N]; vector<int> son[N];
void dfs(int u) { siz[u]=1; for(int v:son[u]) { dfs(v); siz[u]+=siz[v]; } }
signed main(){
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin>>n>>m; T.init(n); For(i,1,m) { int x,y; cin>>x>>y; T.add_edge(x,y); } T.solve(ans);
// For(i,1,n) cerr<<ans[i]<<' '; cerr<<endl;
For(i,2,n) son[ans[i]].push_back(i);
dfs(1); For(i,1,n) cout<<siz[i]<<' '; cout<<endl;
cerr<<"Time = "<<clock()<<" ms\n";
return 0;
}
// START TYPING IF YOU DON'T KNOW WHAT TO DO