一文搞懂Vue Diff演演算法

本篇文章給大家帶來了關於的相關知識，其中主要介紹了關於diff演演算法的相關問題，diff演演算法的作用就是找出兩組vdom節點之間的差異，並儘可能的複用dom節點，使得能用最小的效能消耗完成更新操作，下面一起來看一下，希望對大家有幫助。

前端（vue）入門到精通課程：進入學習
API 檔案、設計、偵錯、自動化測試一體化共同作業工具：

【相關推薦：、】

為什麼需要diff演演算法？

對於一個容器（比如我們常用的#app）而言，它的內容一般有三種情況：

字串型別，即是文字。
子節點陣列，即含有一個或者多個子節點
null，即沒有子節點

在vue中，會將dom元素當作vdom進行處理，我們的HTML Attributes、事件繫結都會現在vdom上進行操作處理，最終渲染成真實dom。

Virtual Dom：用於描述真實dom節點的JavaScript物件。

使用vdom的原因在於，如果每次操作都是直接對真實dom進行操作，那麼會造成很大的開銷。使用vdom時就能將效能消耗從真實dom操作的級別降低至JavaScript層面，相對而言更加優秀。一個簡單的vdom如下：

const vdom = {
    type:"div",
    props:{
        class: "class",
        onClick: () => { console.log("click") }
    },
    children: [] // 簡單理解這就是上述三種內容
}
登入後複製

對於vue節點的更新而言，是採用的vdom進行比較。

diff演演算法便是用於容器內容的第二種情況。當更新前的容器中的內容是一組子節點時，且更新後的內容仍是一組節點。如果不採用diff演演算法，那麼最簡單的操作就是將之前的dom全部解除安裝，再將當前的新節點全部掛載。

但是直接操作dom物件是非常耗費效能的，所以diff演演算法的作用就是找出兩組vdom節點之間的差異，並儘可能的複用dom節點，使得能用最小的效能消耗完成更新操作。

接下來說三個diff演演算法，從簡單到複雜循序漸進。

簡單的Diff演演算法

為什麼需要key？

接下來通過兩種情況進行說明為什麼需要key？

如果存在如下兩組新舊節點陣列：

const oldChildren = [
    {type: 'p'},
    {type: 'span'},
    {type: 'div'},
]
const newChildren = [
    {type: 'div'},
    {type: 'p'},
    {type: 'span'},
    {type: 'footer'},
]
登入後複製

如果我們是進行正常的比較，步驟應該是這樣：

找到相對而言較短的一組進行迴圈對比

第一個p標籤與div標籤不符，需要先將p標籤解除安裝，再將div標籤掛載。
第一個spam標籤與p標籤不符，需要先將span標籤解除安裝，再將p標籤掛載。
第一個div標籤與span標籤不符，需要先將div標籤解除安裝，再將span標籤掛載。
最後多餘一個標籤footer存在在新節點陣列中，將其掛載即可。

那麼我們發現其中進行了7次dom操作，但是命名前三個都是可以複用的，只是位置發生了變化。如果進行復用節點我們需要判斷兩個節點是相等的，但是現在的已有條件還不能滿足。

所以我們需要引入key，它相當於是虛擬節點的身份證號，只要兩個虛擬節點的type和key都相同，我們便認為他們是相等的，可以進行dom的複用。

這時我們便可以找到複用的元素進行dom的移動，相對而言會比不斷的執行節點的掛載解除安裝要好。

但是，dom的複用不意味不需要更新：

const oldVNode = {type: 'p', children: 'old', key: 1}
const newVNode = {type: 'p', children: 'new', key: 2}
登入後複製

上述節點擁有相同的type和key，我們可以複用，此時進行子節點的更新即可。

簡單的diff演演算法步驟

先用一個例子說明整個流程，再敘述其方法

const oldChildren = [
    {type: 'p', children: 'p', key: 1},
    {type: 'span', children: 'span', key: 2},
    {type: 'div', children: 'div', key: 3},
    {type: 'section', children: 'section', key : 4},
]
const newChildren = [
    {type: 'div', children: 'new div', key: 3},
    {type: 'p', children: 'p', key: 1},
    {type: 'span', children: 'span', key: 2},
    {type: 'footer', children: 'footer', key: 5},
]
登入後複製

為了敘述簡單，這裡使用不同的標籤。整個流程如下：

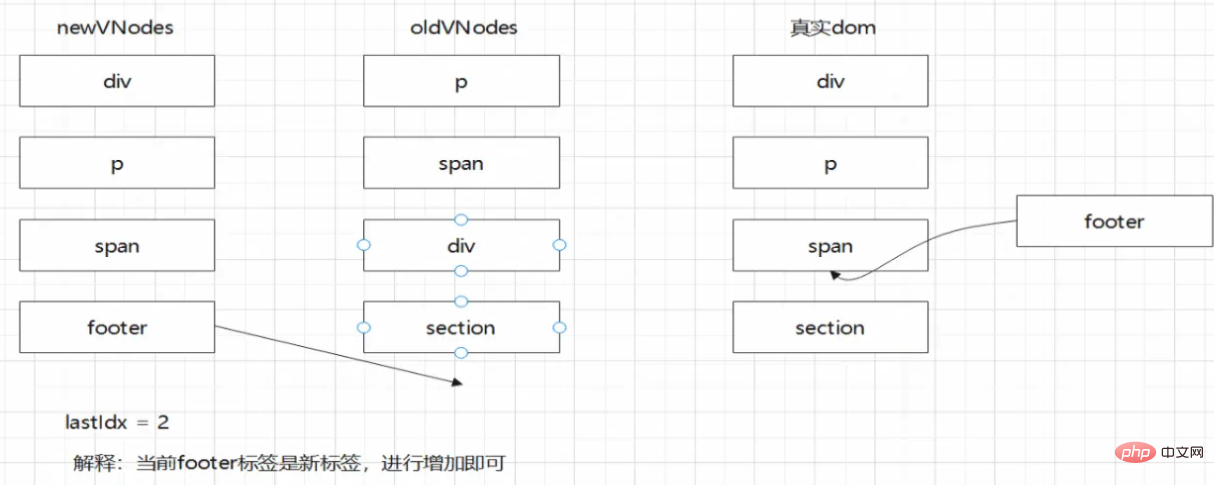
從新節點陣列開始遍歷
第一個是div標籤，當前的下標是0，之前的下標是2。相對位置並未改變，不需要移動，只需要就行更新節點內容即可。
第二個是p標籤，當前的下標是1，之前的下標是0。就相對位置而言，p相對於div標籤有變化，需要進行移動。移動的位置就是在div標籤之後。
第三個是span標籤，當前的下標是2，之前的下標是1。就相對位置而言，p相對於div標籤有變化，需要進行移動。移動的位置就是在p標籤之後。
第四個標籤是footer，遍歷舊節點陣列發現並無匹配的元素。代表當前的元素是新節點，將其插入，插入的位置是span標籤之後。
最後一步，遍歷舊節點陣列，並去新節點陣列中查詢是否有對應的節點，沒有則解除安裝當前的元素。

如何找到需要移動的元素？

上述宣告了一個lastIdx變數，其初始值為0。作用是儲存在新節點陣列中，對於已經遍歷了的新節點在舊節點陣列的最大的下標。那麼對於後續的新節點來說，只要它在舊節點陣列中的下標的值小於當前的lastIdx，代表當前的節點相對位置發生了改變，則需要移動，

舉個例子：div在舊節點陣列中的位置為2，大於當前的lastIdx，更新其值為2。對於span標籤，它的舊節點陣列位置為1，其值更小。又因為當前在新節點陣列中處於div標籤之後，就是相對位置發生了變化，便需要移動。

當然，lastIdx需要動態維護。

總結

簡單diff演演算法便是拿新節點陣列中的節點去舊節點陣列中查詢，通過key來判斷是否可以複用。並記錄當前的lastIdx，以此來判斷節點間的相對位置是否發生變化，如果變化，需要進行移動。

雙端diff演演算法

簡單diff演演算法並不是最優秀的，它是通過雙重回圈來遍歷找到相同key的節點。舉個例子：

const oldChildren = [
    {type: 'p', children: 'p', key: 1},
    {type: 'span', children: 'span', key: 2},
    {type: 'div', children: 'div', key: 3},
]
const newChildren = [
    {type: 'div', children: 'new div', key: 3},
    {type: 'p', children: 'p', key: 1},
    {type: 'span', children: 'span', key: 2},
]
登入後複製

其實不難發現，我們只需要將div標籤節點移動即可，即進行一次移動。不需要重複移動前兩個標籤也就是p、span標籤。而簡單diff演演算法的比較策略即是從頭至尾的迴圈比較策略，具有一定的缺陷。

顧名思義，雙端diff演演算法是一種同時對新舊兩組子節點的兩個端點進行比較的演演算法

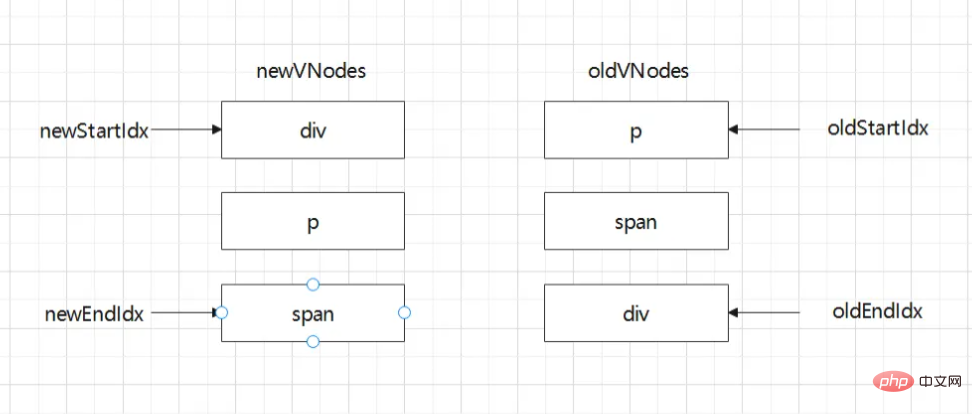
那麼雙端diff演演算法開始的步驟如下：

比較 oldStartIdx節點與 newStartIdx 節點，相同則複用並更新，否則
比較 oldEndIdx節點與 newEndIdx 節點，相同則複用並更新，否則
比較 oldStartIdx節點與 newEndIdx 節點，相同則複用並更新，否則
比較 oldEndIdx節點與 newStartIdx 節點，相同則複用並更新，否則

簡單概括：

舊頭 === 新頭？複用，不需移動
舊尾 === 新尾？複用，不需移動
舊頭 === 新尾？複用，需要移動
舊尾 === 新頭？複用，需要移動

對於上述例子而言，比較步驟如下：

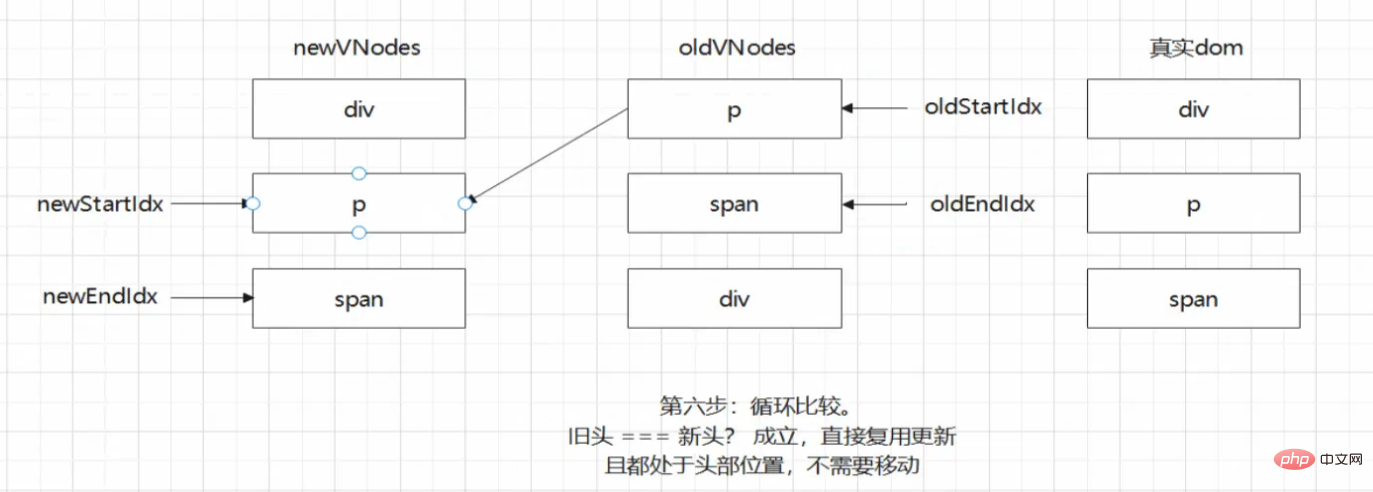
上述的情況是一種非常理想的情況，我們可以根據現有的diff演演算法完全的處理兩組節點，因為每一輪的雙端比較都會命中其中一種情況使得其可以完成處理。

但往往會有其他的情況，比如下面這個例子：

const oldChildren = [
    {type: 'p', children: 'p', key: 1},
    {type: 'span', children: 'span', key: 2},
    {type: 'div', children: 'div', key: 3},
    {type: 'ul', children: 'ul', key: 4},
]
const newChildren = [
    {type: 'div', children: 'new div', key: 3},
    {type: 'p', children: 'p', key: 1},
    {type: 'ul', children: 'ul', key: 4},
    {type: 'span', children: 'span', key: 2},
]
登入後複製

此時我們會發現，上述的四個步驟都會無法命中任意一步。所以需要額外的步驟進行處理。即是：在四步比較失敗後，找到新頭節點在舊節點中的位置，並進行移動即可。動圖示意如下：

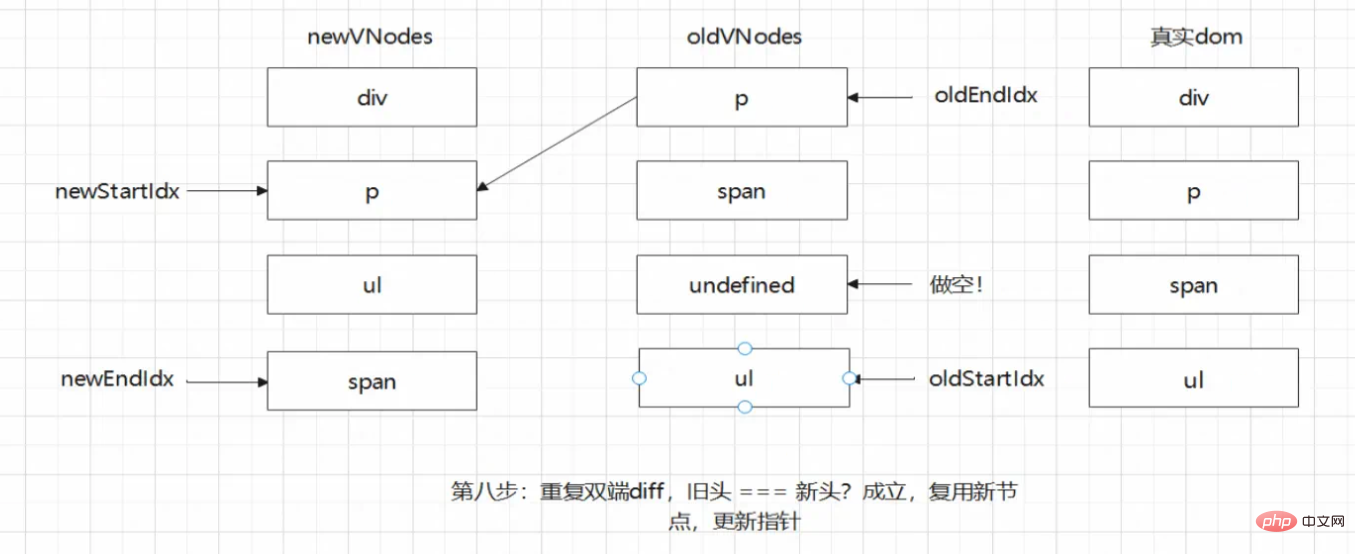
當然還有刪除、增加等均不滿足上述例子的操作，但操作核心一致，這裡便不再贅述。

總結

雙端diff演演算法的優勢在於對於一些比較特殊的情況能更快的對節點進行處理，也更貼合實際開發。而雙端的含義便在於通過兩組子節點的頭尾分別進行比較並更新。

快速diff演演算法

首先，快速diff演演算法包含了預處理步驟。它借鑑了純文字diff的思路，這時它為何快的原因之一。

比如：

const text1 = '我是快速diff演演算法'
const text2 =  '我是雙端diff演演算法'
登入後複製

那麼就會先從頭比較並去除可用元素，其次會重後比較相同元素並複用，那麼結果就會如下：

const text1 = '快速'
const text2 = '雙端'
登入後複製

此時再進行一些其他的比較和處理便會簡單很多。

其次，快速diff演演算法還使用了一種演演算法來儘可能的複用dom節點，這個便是最長遞增子序列演演算法。為什麼要用呢？先舉個例子：

// oldVNodes
const vnodes1 = [
    {type:'p', children: 'p1', key: 1},
    {type:'div', children: 'div', key: 2},
    {type:'span', children: 'span', key: 3},
    {type:'input', children: 'input', key: 4},
    {type:'a', children: 'a', key: 6}
    {type:'p', children: 'p2', key: 5},
]
// newVNodes 
const vnodes2 = [
    {type:'p', children: 'p1', key: 1},
    {type:'span', children: 'span', key: 3},
    {type:'div', children: 'div', key: 2},
    {type:'input', children: 'input', key: 4},
    {type:'p', children: 'p2', key: 5},
]
登入後複製

經過預處理步驟之後得到的節點如下：

// oldVNodes
const vnodes1 = [
    {type:'div', children: 'div', key: 2},
    {type:'span', children: 'span', key: 3},
    {type:'input', children: 'input', key: 4},
    {type:'a', children: 'a', key: 6},
]
// newVNodes 
const vnodes2 = [
    {type:'span', children: 'span', key: 3},
    {type:'div', children: 'div', key: 2},
    {type:'input', children: 'input', key: 4},
]
登入後複製

此時我們需要獲得newVNodes節點相對應oldVNodes節點中的下標位置，我們可以採用一個source陣列，先回圈遍歷一次newVNodes，得到他們的key，再回圈遍歷一次oldVNodes，獲取對應的下標關係，如下：

const source = new Array(restArr.length).fill(-1)
// 處理後
source = [1, 2, 0, -1]
登入後複製

注意！這裡的下標並不是完全正確！因為這是預處理後的下標，並不是剛開始的對應的下標值。此處僅是方便講解。其次，source陣列的長度是剩餘的newVNodes的長度，若在處理完之後它的值仍然是-1則說明當前的key對應的節點在舊節點陣列中沒有，即是新增的節點。

此時我們便可以通過source求得最長的遞增子序列的值為 [1, 2] 。對於index為1，2的兩個節點來說，他們的相對位置在原oldVNodes中是沒有變化的，那麼便不需要移動他們，只需要移動其餘的元素。這樣便能達到最大複用dom的效果。

步驟

以上述例子來說：

首先進行預處理

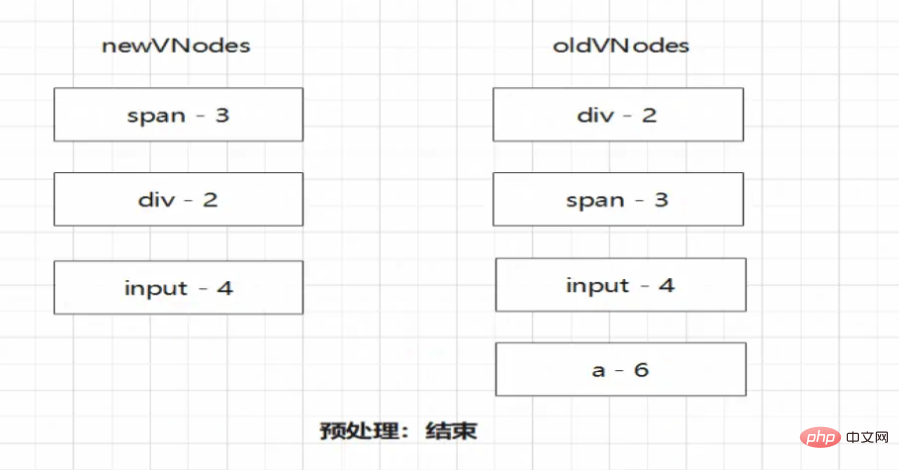
注意！預處理過的節點雖然複用，但仍然需要進行更新。

進行source填充

當然這裡遞增子序列 [1, 2] 和 [0, 1]都是可以的。

進行節點移動

用索引i指向新節點陣列中的最後一個元素

用索引s指向最長遞增子序列中的最後一個元素

然後迴圈進行以下步驟比較：

source[i] === -1？等於代表新節點，掛載即可。隨後移動i

i === 遞增陣列[s]? 等於代表當前的節點存在在遞增子序列中，是複用的節點，當前的節點無需移動。

上述均不成立代表需要移動節點。

節點更新，結束。

總結

核心思路便是進行了類似文字預處理的步驟去除頭尾重複的節點。其次便是採用了最長遞增子序列來複用相對位置沒有發生變化的節點，這些節點是不需要移動的，便能最快的複用和更新。

最後

其實不論是哪一種diff演演算法，它都需要遵循同樣的處理規則：

判斷哪些節點需要移動，以及如何移動。

找出那些需要被新增的或者被移除的節點。

【相關推薦：、】

以上就是一文搞懂Vue Diff演演算法的詳細內容，更多請關注TW511.COM其它相關文章！