技術文章 » 條件期望：Conditional Expectation 舉例詳解之入門之入門之草履蟲都說聽懂了

條件期望：Conditional Expectation 舉例詳解之入門之入門之草履蟲都說聽懂了

2022-10-06 21:00:33

我知道有很多人理解不了 「條件期望」 (Conditional Expectation) 這個東西，有的時候沒看清把隨機變數看成事件，把 \(\sigma\)-algebra 看成隨機變數從而思路全錯的時候，我也會覺得莫名奇妙。所以在這裡用一個極其簡單的例子解釋一下，只要你是一隻上過高中的草履蟲那就能聽懂。

\[\]

我們來丟一枚質地均勻的硬幣（意味著得到正面與反面的概率各為 \(\frac{1}{2}\)），連丟兩次並記錄兩次結果。那麼很容易可以寫出全集 \(\Omega = \left\{ HH, HT, TH, TT \right\}\) ，\(H\) 和 \(T\) 分別代表正面和反面。現在是第一個需要稍加思考的地方，令 \(\mathcal{G}\) 為一個 \(\sigma\)-algebra，其中包括了第一次丟硬幣結果的資訊，請問 \(\mathcal{G}\) 是什麼？



稍加思考，不難得出 \(\mathcal{G} = \left\{\Omega, ~ \emptyset, ~ \left\{ HH, HT \right\}, ~ \left\{ TT, TH \right\} \right\}\)，這裡也做出一個解釋。首先要明確的是，\(\Omega\) 中的元素 (例如 \(HH\)) 和 \(\mathcal{G}\) 中的元素 (例如 \(\left\{ HH, HT \right\}\)) 之間的區別：前者是結果 (outcome)，後者是事件 (event)。我們對於一次 「抽樣」，只能得到一種結果，例如 \(HH\)，代表丟兩次硬幣後得到兩個正面的結果。但不同的結果由於共用某些特性，可以被劃分在同一個事件當中，例如，丟兩次硬幣產生相同的結果應有兩種，即同時為正面或同時為背面 (i.e. \(HH\) 或 \(TT\))，它們歸屬於 「丟兩次硬幣產生相同的結果」 的事件：\(\left\{ HH, TT \right\}\)。回到問題，現在我們已知了第一次丟硬幣後結果的資訊，也就是 "第一次丟硬幣是正面還是背面"，那麼我們自然可以得出 \(\mathcal{G}\) 是由集類：\(\left\{ \left\{ HH, HT \right\}, ~ \left\{TT, TH \right\} \right\}\) 生成的 \(\sigma\)-algebra。這是因為第一次扔硬幣的結果已經被確定——無論它是正面還是背面：如果是正面，那麼結果無非兩種：兩次都正面或第一次正面第二次背面；如果是背面，結果也無非兩種：兩次都背面或第一次背面第二次正面。結合以下樹結構，在得知第一次扔硬幣結果的資訊後，相當於從根 \(XX\) 來到了第一層 \(HX\) 或 \(TX\) （\(X\) 代表未知資訊）。





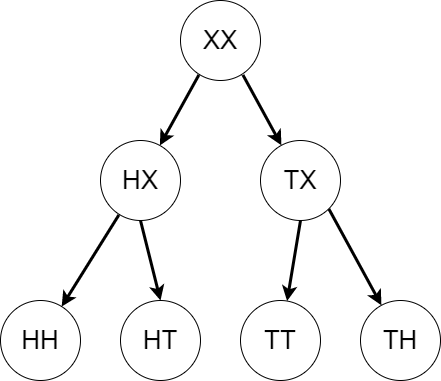
同時，這也從另一個角度說明為什麼概率論最終需要引入 「測度」 的定義——為了描述一種資訊變化的過程。當我們並不知道第一次扔硬幣的結果時，在全空間 \(\Omega\) 上定義的測度空間為 \((\Omega, \mathcal{F}, P)\)，其中：

\[\mathcal{F}:= \left\{ \Omega, ~ \emptyset, ~ \left\{ HH \right\}, ~ \left\{ HT \right\}, ~ \left\{ TH \right\}, ~ \left\{ TT \right\}, ~ \left\{ HH, HT \right\}, \ldots \right\} \]

where \(\mathcal{F}\) 的 cardinality: \(|\mathcal{F}| = 2^{4} = 16\)。

\[\]

而當已知第一次的資訊後，\(\sigma\)-algebra 隨即收縮為：

\[\mathcal{G}:= \left\{ \Omega, ~ \emptyset, ~ \left\{ HH, HT \right\}, ~ \left\{ TH, TT \right\} \right\} \]

\[\]

現在考慮條件期望： \(\mathbb{E}\left[ X ~ | ~ \mathcal{G} \right]\)。其中，\(\mathcal{G}\) 如上記作第一次丟完硬幣後結果的全部資訊，對於 \(\forall w \in \Omega:\) 隨機變數 \(X\) 定義為：

\[X(w) = \begin{cases} a \qquad \mbox{if } ~ w = HH\\ b \qquad \mbox{if } ~ w = HT\\ c \qquad \mbox{if } ~ w = TH\\ d \qquad \mbox{if } ~ w = TT\\ \end{cases} \]

其中 \(a, b, c, d \geq 0\)。



Definition. (Conditional Expectation)

令 \(X\) 為一個定義在 \((\Omega, \mathcal{F}, P)\) 上的非負隨機變數。令 \(G_{1}, G_{2}, \ldots\) 為一個兩兩不相交的事件序列，且對於 \(\forall n \in \mathbb{N}^{+}: ~ P(G_{n}) > 0\)，並且 \(\bigcup\limits_{n\in\mathbb{N}^{+}} G_{n} = \Omega\)。令 \(\mathcal{G}\) 為包含 \(\left\{ G_{1}, G_{2}, \ldots \right\}\) 的最小 \(\sigma\)-algebra，即，任意 \(\mathcal{G}\) 的元素都可以寫作 \(\bigcup\limits_{n \in I} G_{n}\) 的形式，其中 \(I \subset \mathbb{N}^{+}\) (\(I\) 為 \(\mathbb{N}^{+}\) 的某些子集)。那麼：

\[\mathbb{E}\left[ X ~ | ~ \mathcal{G} \right](w) = \mathbb{E}\left[ X ~ | ~ G_{n} \right] = \frac{\mathbb{E}\left[ X \cdot \mathbb{I}_{G_{n}} \right]}{P(G_{n})} \qquad \qquad \mbox{if } w \in G_{n} \]

首先，\(\mathbb{I}_{G_{n}}\)是一個隨機變數，或者說函數：

\[\mathbb{I}_{G_{n}}: \Omega \longrightarrow \left\{ 0, 1 \right\}, \quad x \longrightarrow \mathbb{I}_{G_{n}}(x) = \begin{cases} 1 \qquad \mbox{if } x \in G_{n}\\ 0 \qquad \mbox{otherwise} \end{cases} \]

因此則可以判定，Conditional Expectation \(\mathbb{E}\left[ X ~ | ~ \mathcal{G} \right]\) 算出來也是一個隨機變數，而並非常數。最後，我們可以發現一旦假設 \(w \in G_{n}\)，那麼一定意味著 \(w \notin G_{k}, ~ \forall k \in \mathbb{N}^{+}\setminus\left\{n\right\}\)。



回到扔硬幣的例子。這裡顯然我們有：\(G_{1} = \left\{ HH, HT \right\}, ~ G_{2} = \left\{ TT, TH \right\}\)，且 \(G_{1} \cup G_{2} = \Omega\)。那麼。我們現在只需要依次假設 \(w \in G_{n}\)， 並求 \(\frac{\mathbb{E}\left[ X \cdot \mathbb{I}_{G_{n}} \right]}{P(G_{n})}\)，最後分類討論逐點列出即可。

\[\]

  • 假設 \(w \in G_{1} = \left\{ HH, HT \right\}\)，

\[ \begin{align*} \mathbb{E}\left[ X ~ | ~ \mathcal{G} \right](w) &= \frac{\mathbb{E}\left[ X \cdot \mathbb{I}_{G_{1}}, ~ w \in G_{1} \right]}{P(G_{1})}\\ &= \frac{\sum\limits_{w \in G_{1}}\mathbb{E}\left[ X \cdot \mathbb{I}_{G_{1}} ~ | ~ w \in G_{1} \right] \cdot P\big(\left\{ w \right\}\big)}{P(G_{1})}\\ &= \frac{\sum\limits_{w \in G_{1}} X(w) \cdot P\big(\left\{ w \right\}\big)}{P(G_{1})}\\ & = \frac{X(HH) \cdot P\big( \left\{ HH \right\} \big) + X(HT) \cdot P\big( \left\{ HT \right\} \big)}{P\big( \left\{ HH, HT \right\} \big)}\\ & = \frac{\frac{1}{4} \cdot a + \frac{1}{4} \cdot b}{\frac{1}{2}}\\ & = \frac{a + b}{2} \end{align*} \]

  • 假設 \(w \in G_{2} = \left\{ TT, TH \right\}\)，

\[ \begin{align*} \mathbb{E}\left[ X ~ | ~ \mathcal{G} \right](w) &= \frac{\mathbb{E}\left[ X \cdot \mathbb{I}_{G_{2}}, ~ w \in G_{2} \right]}{P(G_{2})}\\ &= \frac{\sum\limits_{w \in G_{2}}\mathbb{E}\left[ X \cdot \mathbb{I}_{G_{2}} ~ | ~ w \in G_{2} \right] \cdot P\big(\left\{ w \right\}\big)}{P(G_{2})}\\ &= \frac{\sum\limits_{w \in G_{2}} X(w) \cdot P\big(\left\{ w \right\}\big)}{P(G_{2})}\\ & = \frac{X(TT) \cdot P\big( \left\{ TT \right\} \big) + X(TH) \cdot P\big( \left\{ TH \right\} \big)}{P\big( \left\{ TT, TH \right\} \big)}\\ & = \frac{\frac{1}{4} \cdot c + \frac{1}{4} \cdot d}{\frac{1}{2}}\\ & = \frac{c + d}{2} \end{align*} \]

綜上所述：

\[\mathbb{E}\left[ X ~ | ~ \mathcal{G} \right](w) = \begin{cases} \frac{a + b}{2} \qquad \mbox{if } ~ w \in \left\{ HH, HT \right\}\\ \frac{c + d}{2} \qquad \mbox{if } ~ w \in \left\{ TT, TH \right\}\\ 0 \qquad \quad \mbox{otherwise}\\ \end{cases} \]