摘要：學習玩遊戲一直是當今AI研究的熱門話題之一。使用博弈論/搜尋演演算法來解決這些問題需要特別地進行周密的特性定義，使得其擴充套件性不強。使用深度學習演演算法訓練的折積神經網路模型（CNN）自提出以來在影象處理領域的多個大規模識別任務上取得了令人矚目的成績。本文是要開發一個一般的框架來學習特定遊戲的特性並解決這個問題，其應用的專案是受歡迎的手機遊戲Flappy Bird，控制遊戲中的小鳥穿過一堆障礙物。本文目標是開發一個折積神經網路模型，從遊戲畫面幀中學習特性，並訓練模型在每一個遊戲範例中採取正確的操作。本文綜述了基於深度學習的折積神經網路模型在圖形識別（影象識別）中的應用，主要從典型的網路結構的構建、訓練方法和效能表現3個方面進行介紹。

1. 前言

作為深度強化學習的一個很好的入門學習教學，用深度強化學習玩FlappyBird這個範例一直是個很火的程式碼，網上也有不少的文章介紹。不過其大多從程式碼角度介紹，如果需要輸入瞭解其理論與原理我們則需要更多論文資料。這裡我翻譯整理了相關論文並加入些自己的理解寫在這篇博文中，詳細可參考論文Deep Reinforcement Learning for Flappy Bird，具體關於深度強化學習的程式碼介紹將在後面的博文中介紹。

2. 簡介及問題定義

FlappyBird是一款遊戲，玩家控制的物件是遊戲中的「小鳥」，在遊戲執行瞬間有兩個可以採取的動作：按下「上升」鍵，使得小鳥向上跳躍，而未按下任何按鍵時小鳥則以恆定速率下降。

如今，深度學習通過組合低層特徵形成更加抽象的高層表示屬性類別或特徵，以發現資料的分散式特徵表示，使得機器學習模型可以直接學習概念，如直接從原始影象資料進行物體類別分類。深層折積神經網路採用平鋪分層折積濾波器層來模擬視野接受域的影響，在處理計算機視覺問題上，如分類和檢測問題，獲得了很大成功。本文目的是開發一個深層神經網路模型，具體地，是利用影象中的不同物件訓練折積神經網路，進行基於遊戲畫面場景狀態分析進行影象識別分類。從原始畫素中學習遊戲的特性，並決定採取相應行動，本質上是一個對遊戲場景中特定狀態的圖形識別過程，在此設計了一個強化學習系統，通過自主學習來玩這款遊戲。

當通過很少預定的行為進行程式設計不能充分解決問題時，可採用強化學習方式，這是一種通過進行場景訓練，使演演算法在輸入未知和多維資料（如彩色圖片）時做出正確的決策方式。通過這種方式，可以進行線上學習，而且演演算法可以學會自動對影象進行特徵提取，對於訓練中未出現的場景和狀態也同樣可以進行分類和預測。

圖1.FlappyBird遊戲

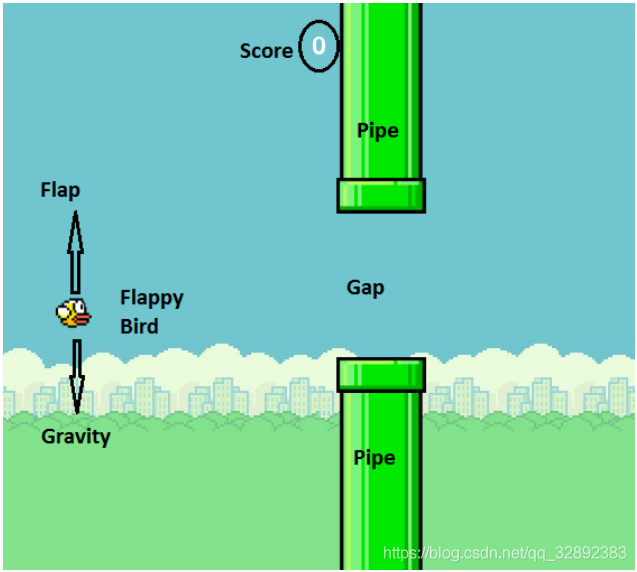
3. 相關工作與實現方法

3.1 相關工作

谷歌DeepMind利用深度學習技術玩遊戲的影響，為從一個完全不同的視角去看待人工智慧問題鋪平了道路。其最新成果人工智慧AlphaGo，在其與圍棋大師的激烈競爭中向人們展示了深度學習的巨大潛力。DeepMind以前僅僅根據遊戲原始圖片就能學習和玩2600種雅達利遊戲。Mnih等人，使用強化學習成功訓練玩這些遊戲的模型，在多種遊戲[1]，[2]中超過了人類專家級別。他們提出了一種新的模型，即結合了深層神經網路的強化學習的深度Q網路（DQN）模型，以深層神經網路作為近似函數代表Q學習中的Q值（動作值）。他們還論述了一些提高訓練效率和穩定性的技術，使用以前經驗的「經驗回放」，從中隨機抽取小批次來更新網路，以便將模型得到的經驗和延遲更新聯絡起來，從而獲得目標值（稍後詳細介紹）以提高穩定性。該通道的另一個優點是完全無需標記的資料，該模型通過與遊戲模擬器的互動，並隨著時間的推移學會做出很好的決策。正是這種簡單的學習模型以及在玩Atari遊戲時的驚人結果，啟發我們採用一個類似的演演算法來完成本文所涉及的專案。

3.2 實現方法

本文是通過訓練一個深度折積神經網路模型（深度Q學習網路）進行特定遊戲狀態下影象的識別與分類。深度Q學習網路是一個經改進過的Q學習演演算法訓練得到的折積神經網路，其輸入是原始的遊戲畫面，輸出是一個評價未來獎勵的價值函數。人工智慧系統的任務是提取遊戲執行的影象，並輸出從可採取的操作集合中提取的必要執行動作。這相當於一個分類問題，不過與常見的分類問題不同，這裡沒有帶標記的資料來訓練模型。可以採用強化學習，根據執行遊戲並基於所觀察到的獎勵來評價一個給定狀態下的動作，以此來進行模型訓練。

3.3 構建模型

遊戲中小鳥可以採取的動作是煽動翅膀向上飛（$a＝1$）或不做任何動作（$a＝0$）。當前狀態（框架）是由經預處理的當前幀原始影象（$X_t$）與有限數量的先前幀影象（$X_{t-1}$, $X_{t-2}$,…）構成。這樣，每一個狀態都將唯一地對應小鳥運動到某一位置所遵循的運動軌跡，從而向模型提供實時資訊，先前儲存的幀數成為超引數。理想情況下，$S_t$是從$t＝1$開始的所有幀的函數，不過為了減少狀態空間，只使用有限的數量幀。如前所述，當鳥撞到管道或螢幕邊緣時，可以給其一個負面獎勵，如果通過了間隙，可得到一個正面的獎勵。這樣可以像人類玩家一樣，儘量避免死亡並儘可能多得分。因此，有兩個獎勵，分別是rewardPass和rewardDie。折扣係數（$\gamma$）為0.9，用於從未來動作貼現的獎勵。

4. Q學習演演算法

強化學習的目標是使總回報（獎勵）最大化。在Q學習中，它是非策略的，迭代更新使用的是貝爾曼方程$$Q_{i+1}(s,a)=r+ \gamma \underset{{a}'}{max}{Q_{i}({s}',{a}') }$$ 其中${s}'$和${a}'$分別是下一幀的狀態和動作，$r$是獎勵，$γ$是折扣因子。$Q_i (s,a)$是為$(s,a)$矩陣在第i次迭代的Q值。這種更新迭代將收斂得到一個最佳的Q函數。為了防止學習僵化，這個動作值函數可以用一個函數（這裡為深度學習網路）近似，以便能更好概括不可預見的狀態。學習演演算法的輸入點由$s_t$, $a_t$, $r_t$, $s_{t+1}$,的列表構成，函數能夠通過這些輸入點來構建一個能最大限度提高整體回報並以此預測動作的模型。將這裡的函數構建為一個折積神經網路，並使用上述方程中的更新規則更新其引數。以下兩個方程為使用損失函數及其梯度來模擬這個函數。

\[L=\sum_{s,a,r,{s}'}(Q(s,a;\theta )-(r+\gamma \underset{{a}'}{max}Q({s}',{a}';\theta^{-})))^{2} \]

\[\Delta_{\theta} L=\sum_{s,a,r,{s}'}-2(Q(s,a;\theta )-(r+\gamma \underset{{a}'}{max}Q({s}',{a}';\theta^{-})))\Delta_{\theta}Q(s,a;\theta) \]

其中，$\theta$是訓練後的DQN引數， $\theta^{-}$（在後面的章節中解釋）是Q值函數的非更新引數。因此，可以簡單地使用上述損失函數的隨機梯度下降法和反向傳播演演算法更新神經網路權重（$\theta$）。演演算法1是為訓練而設計的演演算法，是一種加強探索的$\varepsilon$貪婪演演算法。當訓練進行時，有$\varepsilon$的概率會隨機選擇動作或選擇最優動作$a_{opt}=arg max_{{a}'} Q(s,{a}';θ)$,其中$\varepsilon$隨著更新次數的增加逐漸減小到0。

4.1 預處理

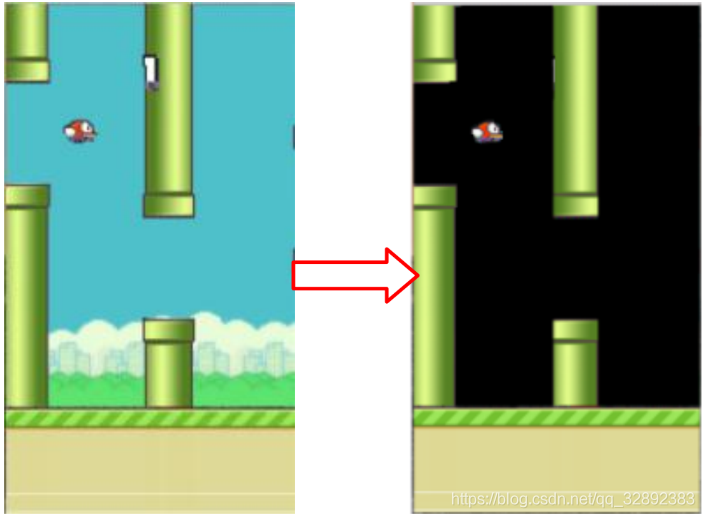
Flappy Bird遊戲直接輸出的畫素是284×512的，但為了節省記憶體將其縮小為84×84大小的影象，每幀影象色階都是0-255。此外，為了提高折積神經網路的精度，在這一步去除背景層並用純黑色背景代替，以去除噪聲，如圖2所示。依次對所得遊戲影象進行縮放、灰度化以及調整亮度處理。在當前幀進入一個狀態之前，處理幾幀影象疊加組合的多維影象資料（如在模型構建部分提到的），當前幀與先前幀重疊時，灰度稍有降低，當我們遠離最新幀時強度降低。因此，這樣輸入的影象將提供關於小鳥當前所在軌跡的良好資訊，其處理過程如圖3所示。

圖2.去除遊戲背景

圖3. 影象處理流程圖（其中紅色塊代表折積層，綠色塊代表最大池化層，藍色部分代表全連線層）

4.2 DQN結構

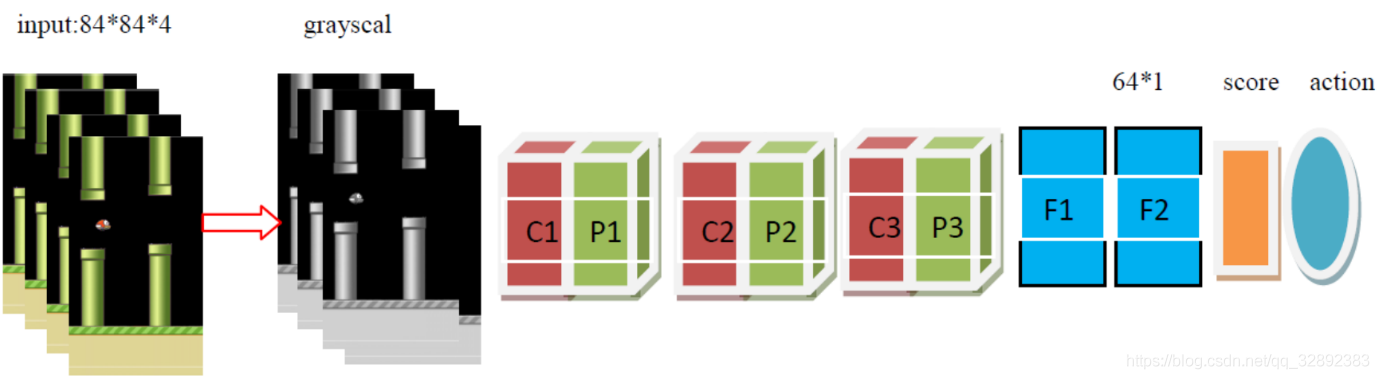
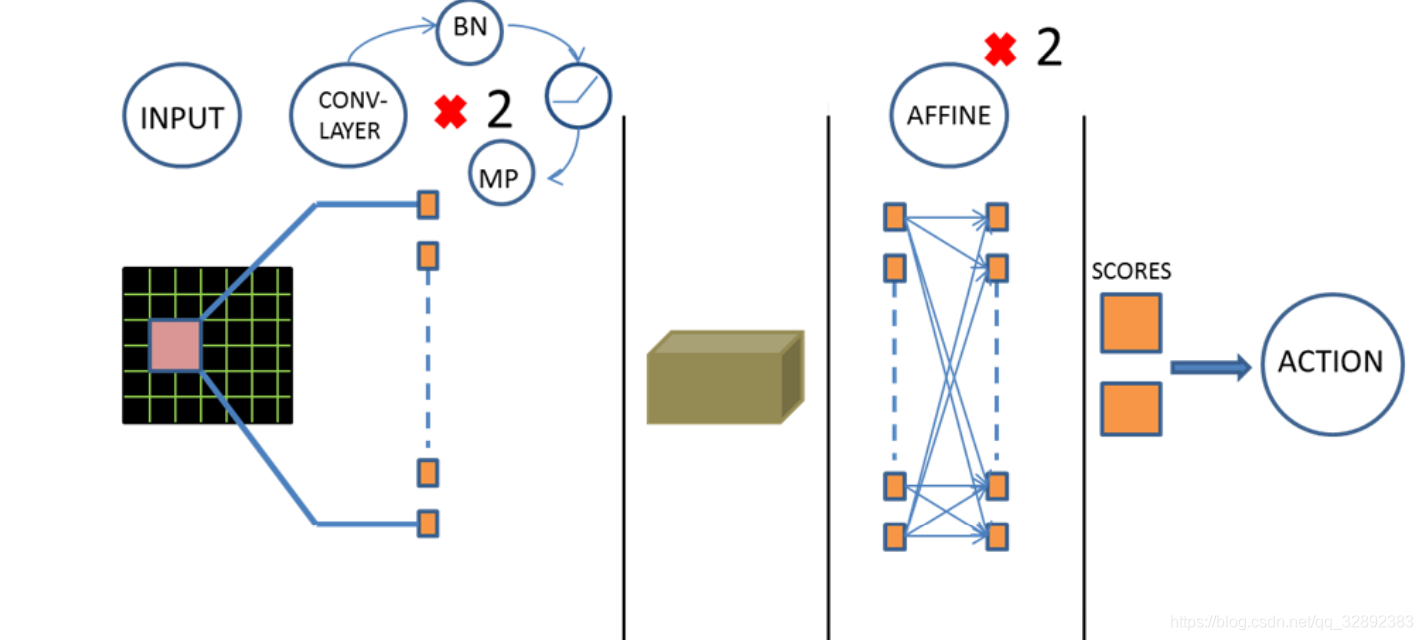
如圖4所示，在當前模型結構中，有3個隱藏層。首先有兩個折積層，然後是兩個完全連線層，最終完全連線層的輸出是兩個動作的得分，結果由損失函數得出。改進的損失函數自動進行Q學習引數設定。遵循空間批次規範，在每個折積層後都新增ReLu和最大池化層。此外，在第一個仿射層（該批規範輸出反饋到最終的仿射層）後是一個ReLu啟用函數和批次處理標準層。折積層採用32個大小為3，步長為1，帶有2×2最大池化核的濾波器。輸入影象的大小84×84，每個時刻有兩種可能的輸出操作，每次動作將會獲得一個得分值，以此決定最佳動作。

表1. 各層引數變化情況

Layer	Input	Filter size	Stride	Num filters	Activation	Output
conv1	84×84×4	8×8	4	32	ReLU	20×20×32
pooling1	20×20×32					10×10×32
conv2	10×10×32	3×3	1	64	ReLU	8×8×64
pooling2	8×8×64					4×4×64
conv3	4×4×64	3×3	1	64	ReLU	2×2×64
pooling3	2×2×64					1×1×64
Fc1	1×1×4					64×1
Fc2	1×64					2×1

考慮到模型處理的精度，可以適當提高模型的複雜度，這裡將折積層的數目改進為3個，同時有3個池化層，兩個全連線層，開始時疊加連續4幀預處理後的影象作為輸入，表1詳細列出了後的模型在每個步驟上的資料尺寸變化及各層引數。

圖4. 折積神經網路結構圖

4.3 經驗回放與穩定性

在Q學習中，以連續方式記錄的經驗資料是高度相關的。若使用相同的順序更新DQN引數，訓練過程就會受到干擾。與從一個標記的資料集中取樣小批次訓練分類模型類似，這裡同樣應該在抽取出的獲得更新的DQN經驗中引入一定的隨機性。為此設定一個經驗回放記憶體，用來儲存每幀遊戲畫面的經驗資料($s_t$,$a_t$,$r_t$,$s_{t+1}$),直到達到其最大儲存容量。重現的經驗資料填充到一定的數量，隨機抽取小批經驗並用於進行DQN引數上的梯度下降。以固定的時間間隔更新DQN引數。由於小批次選擇結果的隨機性，用於更新DQN引數的資料是去相關的。
為了提高損失函數收斂的穩定性，使用方程2中提到的帶引數$\theta ^{-}$的貝爾曼更新方程重現DQN模型。引數$\theta ^{-}$是每次DQN的C值更新之後$\theta$的更新值，用來計算演演算法1中$y_j$的值。

4.4 訓練設計

整個DQN訓練流程如演演算法1所示。如本節前面部分提到的，經驗資料都儲存在回放記憶體中，每隔一段時間，從記憶體隨機取樣出一小批樣本，用於對DQN引數進行梯度下降運算。同網路引數$\theta ^{-}$一樣，必要時需要適當更新探索的概率。

遊戲輸出的得分作為唯一的評價指標，為了使結果具有健壯性，取幾次遊戲的平均得分而不是一次的得分。設定一個衰減值，使$\varepsilon$因子在測試和訓練中逐漸減小為零。這是在更多的訓練和學習時，進行模型決策的保證。

5. 實驗與結果

5.1 訓練引數

模型引數：Flappy Bird遊戲每秒播放10幀，最近的4幀影象處理後進行組合，生成一個狀態；貼現因子$\gamma$設定為0.9；獎勵設定：rewardPass = + 1.0, rewardDie=-1.0。

DQN引數：探索概率$\varepsilon$在600000更新中從0.6線性下降到0。回放記憶體的大小設定為20000，每有500次經驗，就對記憶體資料進行一次小批次取樣。每次C更新到100時，目標模型$\theta ^{-}$的引數更新一次。小批次的32次經驗資料中，隨機抽取每5幀更新DQN引數。

訓練引數：來更新DQN引數的梯度下降更新法是學習率為$1e-6$，$β_1=0.9$，$β_2=0.95$的Adam優化器。在試錯基礎上選擇這些引數，用來觀察損失值的收斂性。折積權重初始化為均值為0，方差為$1e-2$的正態分佈。

5.2 結果與分析

訓練結束後，用模型測試了一些遊戲狀態，以檢測是否能得出合理的結果。圖5示出了一些遊戲場景及其相應的預測分數，其結果顯示模型準確地對狀態進行了分類。

圖5. 範例遊戲場景及其相應的分數。（5a是一個鳥必須跳起來的場景，5b是一個鳥兒必須往下走的場景）

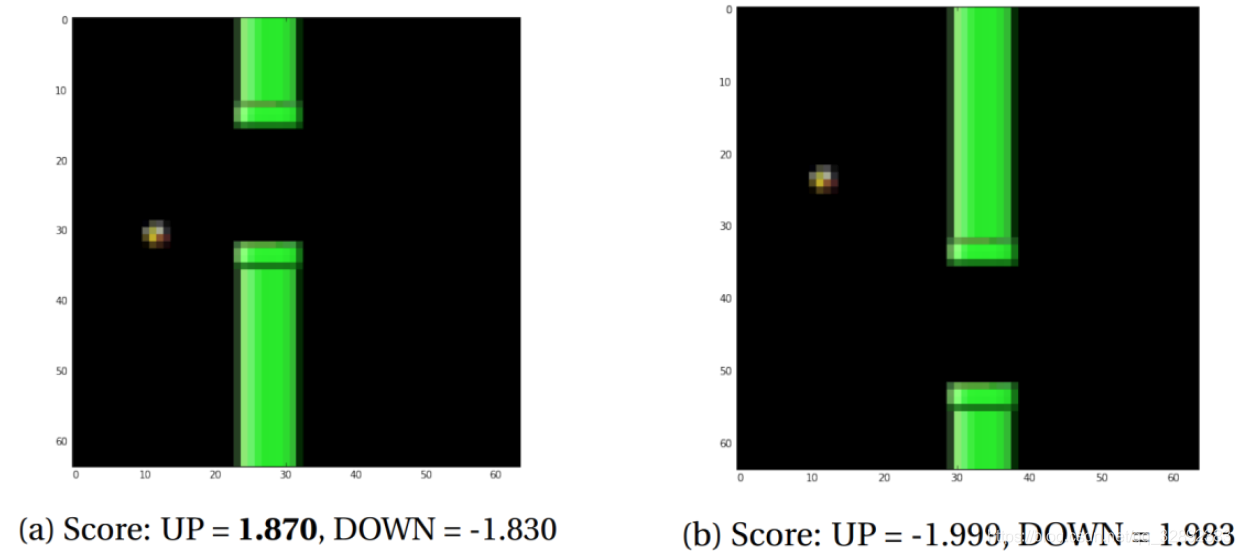
為了更好地理解經過訓練的折積神經網路模型的工作原理，輸出影象5b在經過折積層後的影象，以實現視覺化。可以看出，大多數啟用顯示出空隙和鳥的邊緣處清晰的斑塊（圖6）。可以明顯地推斷，神經網路在學習尋找小鳥與空隙的相對位置。

圖6. 折積層啟用

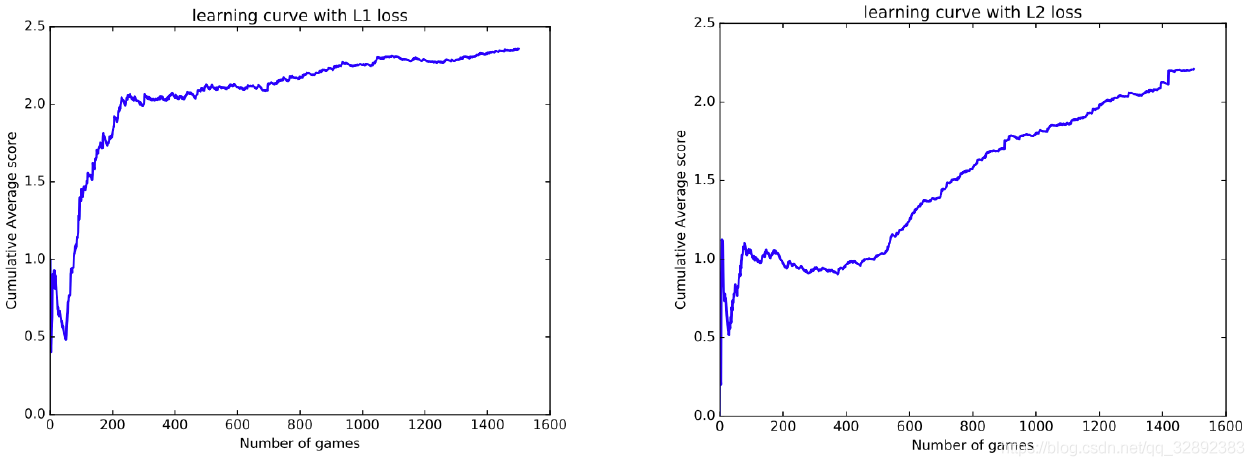
在大多數的在雅達利遊戲上所做得實驗[3]，採用L2的損失函數。這裡嘗試了L1的損失函數（下式）來引入一些正則化。這使得學習率的影象一開始就非常陡峭，如圖7所示。通過這兩種情況可以看出，平均得分穩步上升，表明該模型正在穩步學習。

\[L=\sum_{s,a,r,{s}'}\left |Q(s,a;\theta )-(r+\gamma \underset{{a}'}{max}Q({s}',{a}';\theta^{-}) \right | \]

圖7. 兩種不同損失函數的學習曲線

從表2中可以看出，訓練出的DQN模型取得了遠超人類水平的良好成績，在這樣一個角色扮演的動畫遊戲中，可以看到，儘管有時鳥兒會死亡，但它總是力圖通過水管間的空隙，最可能撞毀的是在間隙的邊緣處。對此可以做的是提高模型的能力，可行的解決方案是使用不同的獎勵方案，讓小鳥走一條遠離管道頂部和底部的路徑。而人類玩家在玩遊戲時也是盡力使小鳥保持在水管間隙中心位置，這同樣可以通過一個精心設計的獎勵方案實現。

表2. 兩種損失函數下模型測試結果

	Human	DQN with L1	DQN with L2
Avg score	4.25	65	72
Max score	21	215	309

5.3 訓練時間

表3. 一定學習率時DQN的平均分

Training iterations	Score
99000	43.6
199000	101.8
299000	35.7
399000	201.3

訓練迭代的次數指的是DQN更新的次數，結果如表3所示，可以看出，更多的訓練次數並不意味著一定能提高模型預測結果的準確性（這裡是對瞬時遊戲狀態下，最佳執行動作的判斷分類）。實際上，更多次的訓練存在許多不穩定性以及結果振盪情況，過多次數的訓練，模型會出現過擬合情況。這些情況需要在進一步的研究中加以解決，一個可能採取的解決方法是訓練時減小學習率或者構建複雜度神經網路模型。

6. 結束語

本文能夠成功地運用深度的強化學習模型來玩遊戲FlappyBird，和傳統的分類任務不同，這裡進行影象識別任務採用的加強學習有個重要優點，即不需要帶標記的資料，完成前面敘述的工作後即可儲存訓練好的模型。模型實現了特定遊戲狀態（模式）下，遊戲執行的最佳動作預測，成功將一個遊戲決策問題轉換成對瞬時多維影象的分類識別問題並運用折積神經網路加以解決。總的來說，結果顯示了深度神經網路在處理影象資訊上的能力，這為許多潛在的應用開闢了道路。

除了強化學習的方式，完成FlappyBird遊戲也可以採用其他方法，如論文Exploring Game Space Using Survival Analysis的通過生存分析的方法，有興趣的可以查閱原文。由於博主能力有限，博文中提及的方法與程式碼即使經過測試，也難免會有疏漏之處。希望您能熱心指出其中的錯誤，以便下次修改時能以一個更完美更嚴謹的樣子，呈現在大家面前。同時如果有更好的實現方法也請您不吝賜教。

參考文獻：
[1] C. Clark and A. Storkey. Teaching deep convolutional neural networks to play go. arXiv preprint arXiv:1412.3409, 2014. 1, 2
[2] V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wierstra, and M. Riedmiller. Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602, 2013. 1, 2
[3] V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness, M. G. Bellemare, A. Graves, M. Riedmiller, A. K. Fidjeland, G. Ostrovski, et al. Human-level control through deep reinforcement learning. Nature, 518(7540):529–533, 2015. 3, 5
[4] D. Silver, A. Huang, C. J. Maddison, A. Guez, L. Sifre, G. van den Driessche, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, M. Lanctot, et al. Mastering the game of go with deep neural networks and tree search. Nature, 529(7587):484–489, 2016. 1

用深度強化學習玩FlappyBird