技術文章 » 詳解機器學習中的資料處理（二）——特徵歸一化

詳解機器學習中的資料處理（二）——特徵歸一化

2022-10-06 12:01:43
功能演示動圖

摘要：在機器學習中，我們的資料集往往存在各種各樣的問題，如果不對資料進行預處理，模型的訓練和預測就難以進行。這一系列博文將介紹一下機器學習中的資料預處理問題，以\(\color{#4285f4}{U}\color{#ea4335}{C}\color{#fbbc05}{I}\)資料集為例詳細介紹缺失值處理、連續特徵離散化，特徵歸一化及離散特徵的編碼等問題，同時會附上處理的\(\color{#4285f4}{M}\color{#ea4335}{a}\color{#fbbc05}{t}\color{#4285f4}{l}\color{#34a853}{a}\color{#ea4335}{b}\)程式程式碼，這篇博文先介紹下特徵歸一化，其要點可見本文目錄。

目錄

\(\color{#4285f4}{點}\color{#ea4335}{擊}\color{#fbbc05}{跳}\color{#4285f4}{轉}\color{#34a853}{至}\color{#ea4335}{博}\color{#4285f4}{文}\color{#ea4335}{涉}\color{#fbbc05}{及}\color{#4285f4}{的}\color{#34a853}{全}\color{#ea4335}{部}\color{#fbbc05}{文}\color{#4285f4}{件}\color{#34a853}{下}\color{#ea4335}{載}\color{#fbbc05}{頁}\)

前言

  這篇博文我會以機器學習中經常使用的\(\color{#4285f4}{U}\color{#ea4335}{C}\color{#fbbc05}{I}\)資料集為例進行介紹。關於\(\color{#4285f4}{U}\color{#ea4335}{C}\color{#fbbc05}{I}\)資料集的介紹和整理，在我前面的兩篇博文：UCI資料集詳解及其資料處理（附148個資料集及處理程式碼）、UCI資料集整理（附論文常用資料集）都有詳細介紹，有興趣的讀者可以點過去了解一下。

  俗話說，「巧婦難為無米之炊」。在機器學習中，資料和特徵便是「米」，模型和演演算法則是「巧婦」。沒有充足的資料、合適的特徵，再強大的模型結構也無法得到滿意的輸出。正如一句業界經典的話所說，「Garbage in，garbage out」。對於一個機器學習問題，資料和特徵往往決定了結果的上限，而模型、演演算法的選擇及優化則是在逐步接近這個上限。

1. 特徵歸一化

  特徵工程，顧名思義，是對原始資料進行一系列工程處理，將其提煉為特徵，作為輸入供演演算法和模型使用。從本質上來講，特徵工程是一個表示和展現資料的過程。在實際工作中，特徵工程旨在去除原始資料中的雜質和冗餘，設計更高效的特徵以刻畫求解的問題與預測模型之間的關係。

  歸一化和標準化都可以使特徵無量綱化，歸一化使得資料放縮在[0, 1]之間並且使得特徵之間的權值相同，改變了原資料的分佈；而標準化將不同特徵維度的伸縮變換使得不同度量之間的特徵具有可比性，同時不改變原始資料的分佈。下面一個小節的方法部分引自諸葛越、葫蘆娃的《百面機器學習》關於特值歸一化的介紹。

特徵歸一化方法

  為了消除資料特徵之間的量綱影響，我們需要對特徵進行歸一化處理，使得不同指標之間具有可比性。例如，分析一個人的身高和體重對健康的影響，如果使用米（m）和千克（kg）作為單位，那麼身高特徵會在1.6～1.8m的數值範圍內，體重特徵會在50～100kg的範圍內，分析出來的結果顯然會傾向於數值差別比較大的體重特徵。想要得到更為準確的結果，就需要進行特徵歸一化（Normalization）處理，使各指標處於同一數值量級，以便進行分析。

  對數值型別的特徵做歸一化可以將所有的特徵都統一到一個大致相同的數值區間內。最常用的方法主要有以下兩種。

  （1）線性函數歸一化（Min-Max Scaling）：它對原始資料進行線性變換，使結果對映到[0, 1]的範圍，實現對原始資料的等比縮放。歸一化公式如下：

\[X_{norm}=\frac{X-X_{min}}{X_{max}-X_{min}}\tag{1.1} \]

其中\(X\)為原始資料，\(X_{max}\)、\(X_{min}\)分別為資料最大值和最小值。

  （2）零均值歸一化（Z-Score Normalization）：它會將原始資料對映到均值為0、標準差為1的分佈上。具體來說，假設原始特徵的均值為\(\mu\)、標準差為\(\sigma\)，那麼歸一化公式定義為：

\[z=\frac{x-\mu }{\sigma }\tag{1.2} \]

  為什麼需要對數值型特徵做歸一化呢？我們不妨藉助隨機梯度下降的範例來說明歸一化的重要性。假設有兩種數值型特徵，\(x_{1}\)的取值範圍為[0, 10]，\(x_{2}\)的取值範圍為[0, 3]，於是可以構造一個目標函數符合圖1.1 (a)中的等值圖。在學習速率相同的情況下，\(x_{1}\)的更新速度會大於\(x_{2}\)，需要較多的迭代才能找到最優解。如果將\(x_{1}\)和\(x_{2}\)歸一化到相同的數值區間後，優化目標的等值圖會變成圖1.1 (b)中的圓形，\(x_{1}\)和\(x_{2}\)的更新速度變得更為一致，容易更快地通過梯度下降找到最優解。

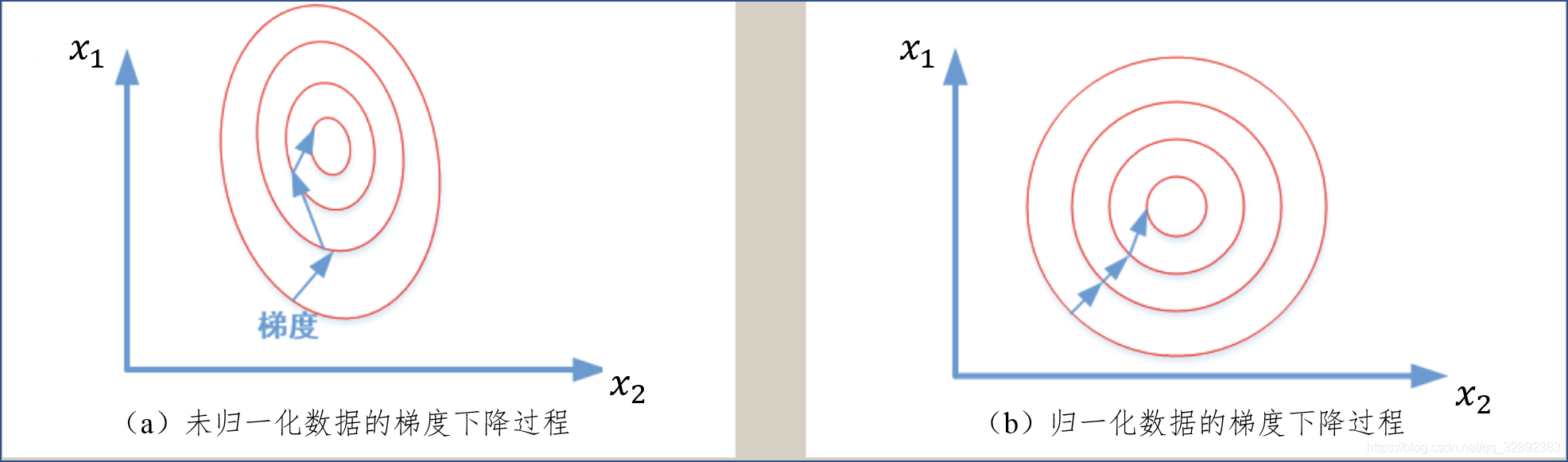
功能演示動圖
圖1.1 資料歸一化對梯度下降收斂速度產生的影響

  在實際應用中，通過梯度下降法求解的模型通常是需要歸一化的，包括線性迴歸、邏輯迴歸、支援向量機、神經網路等模型。當然，資料歸一化並不是萬能的，這一方法對於決策樹模型並不適用。

Matlab程式碼實現

  這裡我給大家介紹下如何用程式碼實現。在\(\color{#4285f4}{M}\color{#ea4335}{a}\color{#fbbc05}{t}\color{#4285f4}{l}\color{#34a853}{a}\color{#ea4335}{b}\)中對於上面提到的兩種歸一化方法均有自帶的處理常式，為避免二次開發我們使用其自帶的函數，它們分別是最大最小值對映：mapminmax( )和z值標準化：zscore( )。這裡我們分別介紹以下這兩個函數，mapminmax( )函數官方檔案介紹如下：

mapminmax
通過將行的最小值和最大值對映到[ -1 1] 來處理矩陣
語法
[Y,PS] = mapminmax(X,YMIN,YMAX)
[Y,PS] = mapminmax(X,FP)
Y = mapminmax('apply',X,PS)
說明
[Y,PS] = mapminmax(X,YMIN,YMAX) 通過將每行的最小值和最大值歸一化為[ YMIN，YMAX] 來處理矩陣。
[Y,PS] = mapminmax(X,FP) 使用結構體作為引數： FP.ymin，FP.ymax。
Y = mapminmax('apply',X,PS) 給定 X和設定PS，返回Y。

——MATLAB官方檔案

  mapminmax( )函數是按行進行歸一化處理的，我們可以通過在命令列鍵入指令進行測試，由於資料集中的資料屬性是按列的所以在計算時需要對矩陣進行轉置，測試指令和執行結果如下：

>> x1 = [1 2 4; 1 1 1; 3 2 2; 0 0 0]

x1 =

     1     2     4
     1     1     1
     3     2     2
     0     0     0

>> [y1,PS] = mapminmax(x1');
>> y1'

ans =

   -0.3333    1.0000    1.0000
   -0.3333         0   -0.5000
    1.0000    1.0000         0
   -1.0000   -1.0000   -1.0000

  zscore( )的使用檔案介紹如下，該函數按列將每個元素歸一化為均值到0，標準差為1的分佈上，詳情可參考zscore( )函數官方檔案。

zscore
z值標準化
語法
Z = zscore(X)
Z = zscore(X,flag)
Z = zscore(X,flag,'all')
說明
Z = zscore(X) 為X的每個元素返回Z值，將X每列資料對映到均值為0、標準差為1的分佈上。Z與的大小相同X。
Z = zscore(X,flag) 使用由flag表示的標準偏差來縮放X。
Z = zscore(X,flag,'all') 使用X中的所有值的平均值和標準偏差來歸一化X。

——MATLAB官方檔案

  zscore( )函數是按列的均值和標準差進行歸一化處理的，我們可以通過在命令列鍵入指令進行測試，測試指令和執行結果如下：

>> x2 = [1 2 4; 1 1 1; 3 2 2; 0 0 0]

x2 =

     1     2     4
     1     1     1
     3     2     2
     0     0     0

>> y2 = zscore(x2);
>> y2

y2 =

   -0.1987    0.7833    1.3175
   -0.1987   -0.2611   -0.4392
    1.3908    0.7833    0.1464
   -0.9934   -1.3056   -1.0247

  對此我們以UCI資料集中的wine( )資料集為例對其資料進行線性函數歸一化及零均值歸一化，首先在官網下載頁下載並儲存檔案「wine.data」儲存在自定義資料夾下，用\(\color{#4285f4}{M}\color{#ea4335}{a}\color{#fbbc05}{t}\color{#4285f4}{l}\color{#34a853}{a}\color{#ea4335}{b}\)開啟檔案部分資料截圖如下圖所示：

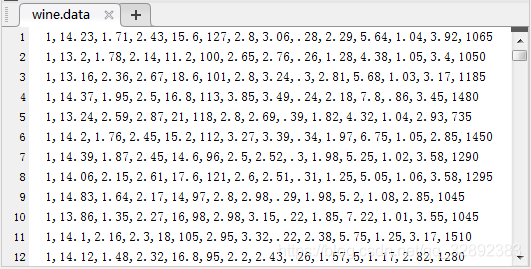
功能演示動圖

  在該目錄下新建\(\color{#4285f4}{M}\color{#ea4335}{a}\color{#fbbc05}{t}\color{#4285f4}{l}\color{#34a853}{a}\color{#ea4335}{b}\)檔案「data_normal.m」並在編輯器中鍵入如下程式碼：

% Normalization
% author:sixu wuxian, website:https://wuxian.blog.csdn.net

clear;
clc;

% 讀取資料
wine_data = load('wine.data'); % 讀取資料集資料
data = wine_data(:,2:end);     % 讀取屬性
label = wine_data(:, 1);       % 讀取標籤

% y =（ymax-ymin）*（x-xmin）/（xmax-xmin）+ ymin;
xmin = -1;
xmax = 1;
[y1, PS] = mapminmax(data', xmin, xmax); % 最大最小值對映歸一化
mapminmax_data = y1'; 
save('wine_mapminmax.mat', 'mapminmax_data', 'label'); % 儲存歸一化資料

% y = (x-mean)/std
zscore_data = zscore(data);  % 零均值歸一化
save('wine_zscore.mat', 'zscore_data', 'label');% 儲存歸一化資料

  以上程式碼執行後將結果分別儲存在檔案「wine_mapminmax.mat」和「wine_zscore.mat」中，通過工作區的變數顯示情況可以看出資料已歸一化到較理想情況，如下圖所示：

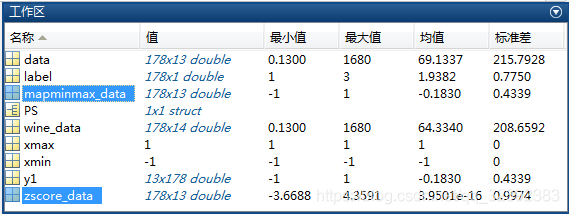
功能演示動圖

2. 程式碼資源獲取

  這裡對博文中涉及的資料及程式碼檔案做一個整理，本文涉及的程式碼檔案如下圖所示。所有程式碼均在\(\color{#4285f4}{M}\color{#ea4335}{a}\color{#fbbc05}{t}\color{#4285f4}{l}\color{#34a853}{a}\color{#ea4335}{b}\) \(\color{#4285f4}{R}\color{#ea4335}{2}\color{#fbbc05}{0}\color{#4285f4}{1}\color{#34a853}{6}\color{#ea4335}{b}\)中偵錯通過，點選即可執行。

功能演示動圖

後續博文會繼續分享資料處理系列的程式碼，敬請關注博主的機器學習資料處理分類專欄。

【資源獲取】

  若您想獲得博文中介紹的填充缺失資料涉及的完整程式檔案（包含資料集的原始檔案、歸一化程式碼檔案及整理好的檔案），可點選下方卡片關注公眾號「AI技術研究與分享」，後臺回覆「NM20200301」，後續系列的程式碼也會陸續分享打包在裡面。

  更多的UCI資料及處理方式已打包至博主麵包多網頁，裡面有大量的UCI資料集整理和資料處理程式碼，可搜尋思緒無限查詢。

結束語

  由於博主能力有限，博文中提及的方法即使經過試驗，也難免會有疏漏之處。希望您能熱心指出其中的錯誤，以便下次修改時能以一個更完美更嚴謹的樣子，呈現在大家面前。同時如果有更好的實現方法也請您不吝賜教。

【參考文獻】

[1] https://ww2.mathworks.cn/help/deeplearning/ref/mapminmax.html
[2] https://ww2.mathworks.cn/help/stats/zscore.html