一、前言

有一定數學基礎的同學們都知道，如果兩個正整數相除之後得到的結果，要麼能除盡，要麼就是一個迴圈小數。
假如結果是迴圈小數，那麼小數的每一位取值是0-9，且存在迴圈節點。如果我們用小數的每一位進行畫圖，每位小數用固定的線段表示，而每位小數的大小則用角度(1代表36度，2代表72度，以此類推)表示，這樣的話我們就可以看到畫圖板上有一條線段在行走一樣。
範例：
1/7=0.142857142857142857…
第1位小數是1，則畫一條長度固定，角度為72°的線段，接著第2位小數是4，在原線段基礎上畫一條長度固定，角度為144°的線段，依次類推，就會形成如下圖案：

只要是迴圈小數，最後都會形成一個對稱的圖形。如上圖，感覺還是挺好看的。或許這就是數學之美吧~

二、準備

2.1 用到的庫

decimal：高精度庫，可以用來計算更高精度的小數。
turtle：大名鼎鼎的海龜畫相簿，用來畫圖。

2.2 原理介紹

1、使用高精度庫計算2個數位相除之後的結果，最好精確到200位以上。
2、編寫一個函數，用來求第一步結果的小數部分並做處理，求到這個小數的固定部分及迴圈位數。例如：1/12=0.08333333，那麼固定部分就是：08，迴圈部分就是：3。
3、為了能用盡量少的畫筆畫成最終的圖形(形成對稱)，我們需要用固定部分+迴圈部分*10的小數位來進行畫圖。

三、範例

3.1 完整程式碼

# Encoding: utf-8
# Author: 思必得
# Date: 2021-09-29 14:21
# Project name: FrbPythonFiles
# IDE: PyCharm
# File name: walknumber

# 模組說明：
"""
"""
# 更新紀錄檔：
"""
1、2021-09-29：
    a、完成初版
"""
# 待修改：
"""
"""


def 求兩個數相除之後的小數部分的迴圈小數(p_dividend: int, p_divisor: int, p_prec: int = 500):
    """
    求兩個整數相除之後的小數部分的迴圈小數，包括4部分：固定部分 + 迴圈部分 + 固定部分的長度 + 迴圈部分的長度
    比如1/7=0.142857142857142857142857142857，那麼最後返回：('', '142857', 0, 6)
    @param p_dividend: 被除數
    @param p_divisor: 除數
    @param p_prec: 小數的精確度(精確到多少位)
    @return: {tuple：固定部分 + 迴圈部分 + 固定部分的長度 + 迴圈部分的長度}
    @author: 思必得
    @note：呼叫範例:
    (1, 95)     ('0', '105263157894736842', 1, 18)
    (1, 97)     ('', '010309278350515463917525773195876288659793814432989690721649484536082474226804123711340206185567', 0, 96)
    (1, 193)    迴圈部分的長度：192位
(1, 479)    迴圈部分的長度：239位
(1, 384)    固定部分的長度：7位
    """
    from decimal import getcontext, Decimal
    getcontext().prec = p_prec  # 設定精度

    if p_dividend % p_divisor == 0:  # 整除的情況
        return None
    _shang_str = str(Decimal(p_dividend) / Decimal(p_divisor))
    _index = _shang_str.find('.')
    _str_digits = _shang_str[_index + 1:]
    _len_digits = len(_str_digits)
    if len(_shang_str) - 1 < p_prec:  # 非迴圈小數
        return None

    _half = _len_digits // 2
    for i in range(_half):
        for j in range(1, _half - i):
            _ratio = (_len_digits - i) // j
            _lt = _str_digits[slice(i)] + _str_digits[slice(i, i + j)] * _ratio
            _lt = _lt + _str_digits[slice(i, i + j)][slice(_len_digits - len(_lt))]
            if _lt[:-1] == _str_digits[:-1]:
                _fix = _str_digits[slice(0, i)]
                _loop = _str_digits[slice(i, i + j)]
                return _fix, _loop, len(_fix), len(_loop)


if __name__ == '__main__':
    import turtle as tt

    if s := 求兩個數相除之後的小數部分的迴圈小數(1, 13):
        ss = s[0] + s[1] * 10
        print(s)
        print(ss, len(ss))
        tt.setup(width=1.0, height=1.0)
        pen = tt.Pen()
        for i in ss:
            pen.left(int(i) * 36)
            pen.forward(100)
        tt.exitonclick()
    else:
        print('無法作圖，結果不是迴圈小數')

3.2 一些結果

3.2.1 1/11

('', '09', 0, 2)

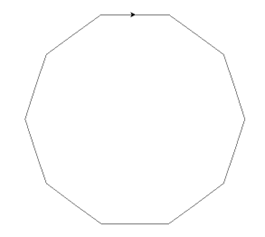
3.2.2 1/13

('', '076923', 0, 6)

3.2.3 1/17

('', '0588235294117647', 0, 16)

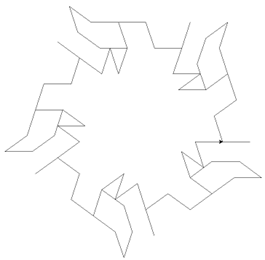
3.2.4 1/19

('', '052631578947368421', 0, 18)

行走的數位