技術文章 » 【近似最近鄰搜尋】在茫茫點集中，怎麼找到你的鄰居

【近似最近鄰搜尋】在茫茫點集中，怎麼找到你的鄰居

2022-10-05 18:00:26

轉載請註明出處

一、背景

我們從最最最簡單的場景開始，假設在一個二維平面上，現有N個點，如下圖所示

現在給你一個點，求K個最近的點（歐式距離），如下圖所示

肉眼很容易可以看出，以query點為中心畫個圓，慢慢往外擴充套件，直到包含K個點，然後這K個點就是最近的點。
看起來很容易，但這得給演演算法實現個眼睛啊！

二、暴力解法

這裡需要遍歷所有的N個點跟query點分別求個距離，然後找出K個最相近的點。
咱們專注於這個演演算法本身，假設距離計算的複雜度為1，那麼暴力解法的複雜度為：N + NlogK

假設N很大，在沒有考慮距離計算的複雜度前提下，其實這複雜度已經很高了。那如果是單機，估計實現不了線上實時計算了，有沒有辦法解決呢？

三、分散式解法

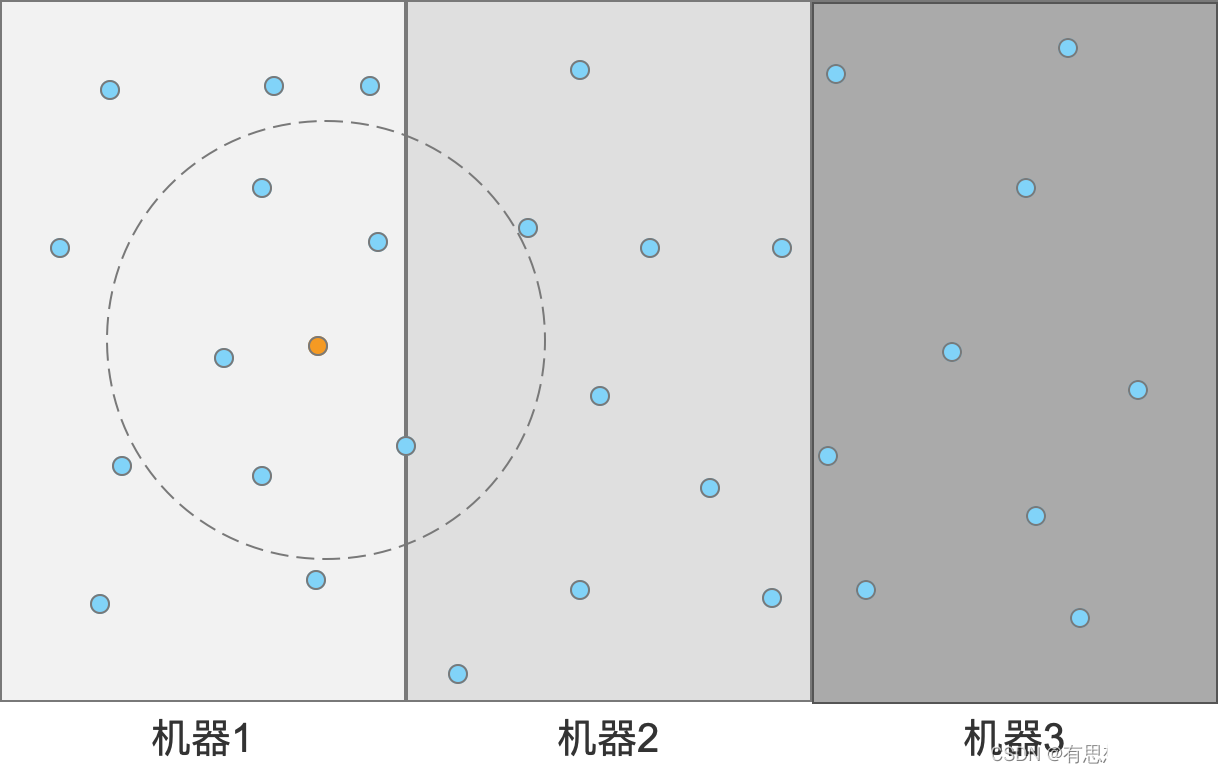
把點隨機分佈到不同機器上，然後求解的時候每臺機器都算個top K出來，再合併。如下圖所示：

其實這樣整體複雜度並沒有變化，只是利用機器資源換取時間，理論上只要機器夠多，耗時還是能降低很多的。

如果沒有很多機器資源，可以考慮下更優的解法。

四、分散式解法優化——IVF

既然都已經把N個點劃分成A(3)個區域了，劃分方法能否考慮下距離？比如最簡單的按距離劃分，如圖所示：

這時我們在檢索的時候，只需要在最近的B(>A=3)個區域暴力檢索就行了。
如果A=3，B=1，那麼複雜度就是： (N+NlogK)/3，這個複雜度是有很大的降低的，但是會有一個缺點，精度有所降低。如果上圖所示，劃分後的結果，會導致一個點出錯～

實際構建區域步驟

  1. 對所有點集合抽樣一份小的集合。
  2. 利用聚類演演算法（一般是Kmean）得出A個聚類中心點。
  3. 把所有點都按距離分配到每個聚類中心，得到A個點集合。

實際檢索步驟

  1. 在A個聚類中心點中，暴力找出B個最近的聚類中心點
  2. 只在B個聚類中心點所屬點集中，暴力檢索最近的top K個點

實際複雜度

(N + NlogK)B/A + A
A為聚類中心個數，B為檢索查詢的聚類中心數

雖然這種方法已經大大降低了複雜度，但還有更有的方式嗎？

五、圖論演演算法——NSW

其實就是把N個點按一定規則連邊，構成一個有向圖，如下圖所示：

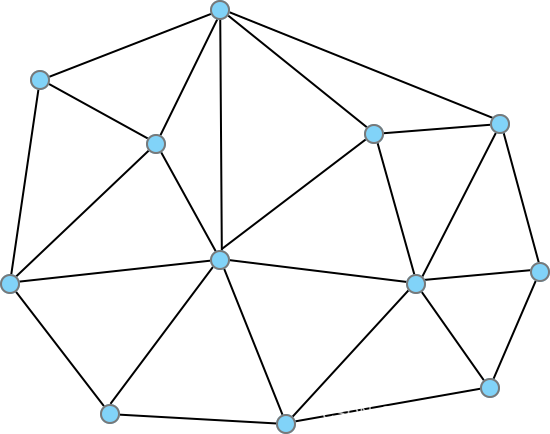
藍色點為點集，黑色邊為有向邊，具體如何構造這個有向邊後邊再說，先說下檢索流程

檢索流程

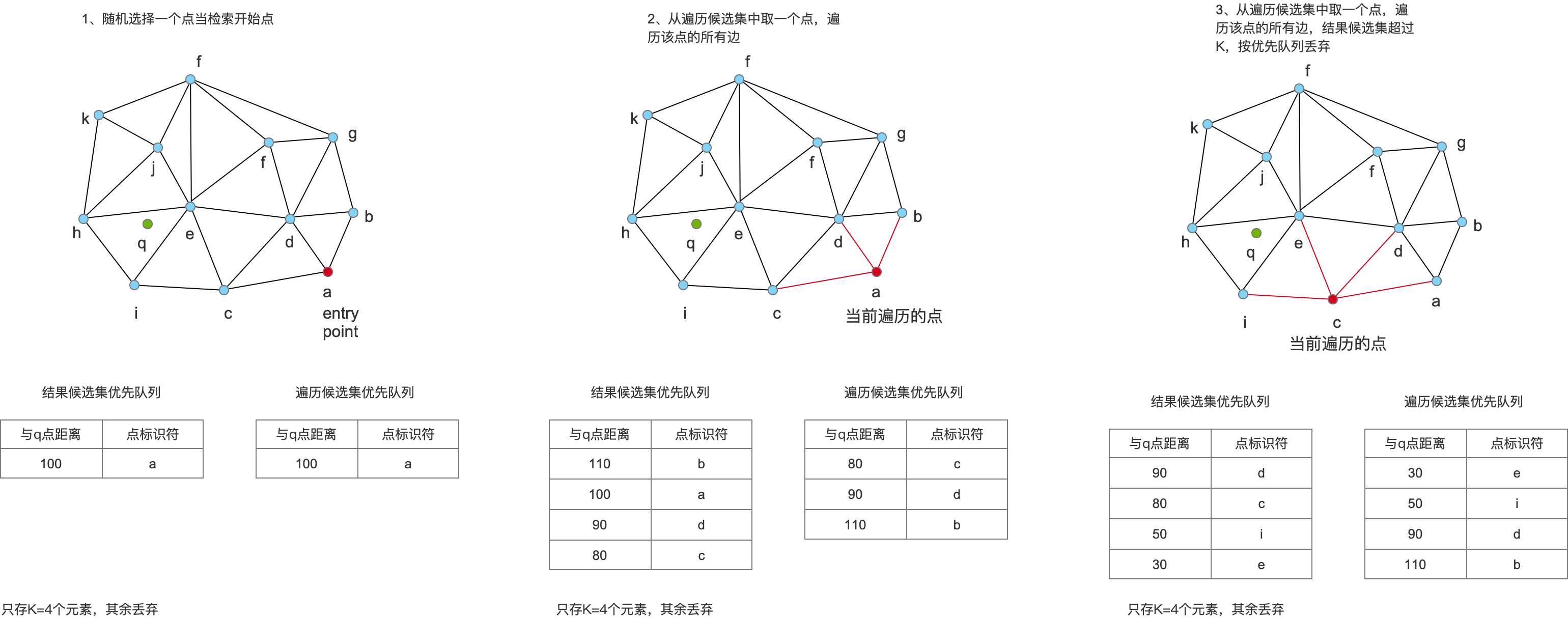
如下圖所示：

  1. 給出一個query點，如上圖 紅色點

  2. 初始化一個點集存取記錄儲存

  3. 初始化兩個優先佇列，一個儲存結果候選集，只存K個元素，一個儲存遍歷候選集

  4. 隨機找一個點，當作進場開始點（如上圖右下角紅點，entry point）

  5. entry point 加入遍歷候選集，如果它並不是標記為刪除的，把它放入結果候選集；

  6. 從遍歷候選集中取出距離query點最近的點，遍歷與它所有關聯的點，檢查是否已經存取過

    • 如果它已經存取過，直接跳過
    • 如果沒有存取過加入遍歷候選集，如果關聯點並不是標記為刪除的，把它放入結果候選集。

  7. 重複第6步驟，直到遍歷候選集中距離query最近的點，都比結果候選集距離query最遠的點距離query大，並且結果候選集已經足夠K個點就結束。

新增構建步驟

  1. 給出一個待新增的點 A
  2. 在圖中檢索出top k個點，k = ef_construction
  3. 從點A 連線其中M_個點，這M_個點從 top k裡面選擇，後面簡稱M_個點裡面當前遍歷的點為點B
  4. 遍歷每條新增連邊，檢查是否有相應的反向連邊，也就是從點B到點A的連邊
    • 如果有就跳過
    • 如果沒有就給反向邊連上
      • 如果點B的連邊沒有超過M_， 直接連上就行
      • 如果點B的連邊超過了M_， 需要重新選擇M_個點，保證點B只有外出M_條邊

簡單的說，其實就是找出top k近鄰，然後連邊。重點問題在於，如果 K > M_，怎麼選擇更加合適的鄰居呢？

最簡單的方式：按距離排序，選擇跟新增點最近的那些。這樣有可能形成孤島，導致整個圖並不是連通圖，有沒有更好的方式呢？

優質鄰居選擇方式

如下圖所示：

  1. 給出一個query點（黃色），top K結果候選集（紅色）

  2. 初始化一個結果候選集的優先佇列，一個優質鄰居列表

  3. 從結果候選集取出一個點，判斷該點與query的距離，是不是比該點與優質鄰居的距離都大

    • 如果是，加入優質鄰居列表
    • 如果不是，丟棄

其實就是把連邊的點儘量分散。

更新點構建步驟

  1. 初始化兩個set 集合A、B
  2. 集合A存更新點的所有鄰居，集合B存更新點的 所有鄰居 & 所有鄰居的鄰居
  3. 給集合A裡面的所有點，從集合B裡面重新選擇合適的鄰居
  4. 重新跑一遍新增點的流程，見上面的新增

六、圖論演演算法優化——HNSW

其實它就是 Skip list + NSW，我們先回顧下跳錶的結構吧。

跳錶


這是一種很常見的資料結構，這裡就不詳細描述了。

真正的HNSW結構


如上圖所示，其實HNSW 就是 Skip List + NSW。
跳錶也是分層的，但是真正的跳錶每一層是一條有序列表。
然而在HNSW中，也是跟跳錶一樣分層，這裡每一層就是一個NSW有向圖。

加上跳錶思想後，nsw的操作只有一個不同的點。檢索進場點是上一層的得到的最近的點，當然最上面一層還是隨機點進場。

這種演演算法複雜度理論上是logN的，當然也只是理論上哈，而且又一定的精度損失～

實際場景

實際場景上

  • 如果記憶體夠大能撐住NSW所需的記憶體，可以考慮直接上HNSW
  • 如果記憶體不夠，可以考慮IVF + HNSW 或者 直接隨機分佈 + HNSW