初等數論學習筆記 III：數論函數與篩法

• 初等數論學習筆記 I：同餘相關。
• 初等數論學習筆記 II：分解質因數。

1. 數論函數

本篇筆記所有內容均與數論函數相關。因此充分了解各種數論函數的名稱，定義，符號和性質是必要的。

1.1 相關定義

• 數論函數：定義域為正整數的函數稱為 數論函數。因其在所有正整數處均有定義，故可視作數列。OI 中常見的數論函數的陪域（即可能的取值範圍）為整數。
• 加性函數：若對於任意 \(a, b\in \mathbb{N}_+\) 且 \(a\perp b\) 均有 \(f(ab) = f(a) + f(b)\)，則稱 \(f\) 為 加性函數。注意區分代數中的加性函數。
• 積性函數：若對於任意 \(a, b\in \mathbb{N}_+\) 且 \(a\perp b\) 均有 \(f(ab) = f(a)f(b)\)，則稱 \(f\) 為 積性函數。易知 \(f(1) = 1\) 是必要條件。
• 完全積性函數：若對於任意 \(a, b\in \mathbb{N}_{+}\) 均有 \(f(ab) = f(a)f(b)\)，則稱 \(f\) 為 完全積性函數。完全積性函數一定是積性函數。
• 數論函數的 加法：對於數論函數 \(f, g\)，\(f + g\) 表示 \(f\) 和 \(g\) 對應位置相加，即 \((f + g)(x) = f(x) + g(x)\)。
• 數論函數的 數乘：對於數 \(c\) 和數論函數 \(f\)，\(c\cdot f\) 表示 \(f\) 的各個位置乘 \(c\)，即 \((c\cdot f)(x) = c \cdot f(x)\)。一般簡記作 \(cf\)。
• 數論函數的 點乘：對於數論函數 \(f, g\)，\(f \cdot g\) 表示 \(f\) 和 \(g\) 對應位置相乘，即 \((f \cdot g)(x) = f(x)g(x)\)。為與狄利克雷折積符號 \(*\) 作區分，點乘符號通常不省略。

1.2 常見數論函數

設 \(n\) 的唯一分解為 \(\prod\limits_{i = 1} ^ m p_i ^ {c_i}\)，以下是一些常見數論函數：

• 單位函數：\(\epsilon(n) = [n = 1]\)。當 \(n = 1\) 時取值為 \(1\)，否則取值為 \(0\)。它是完全積性函數。
• 常數函數：\(1(n) = 1\)。它是完全積性函數。
• 恆等函數：\(\mathrm{id}_k(n) = n ^ k\)。\(\mathrm{id}_1(n)\) 記作 \(\mathrm {id}(n)\)。它是完全積性函數。
• 除數函數：\(\sigma_k(n) = \sum\limits_{d\mid n}d ^ k\)。\(\sigma_0(n)\) 表示 \(n\) 的約數個數，記作 \(\tau(n)\) 或 \(d(n)\)。\(\sigma_1(n)\) 表示 \(n\) 的約數和，記作 \(\sigma(n)\)。\(\sigma_k(n)\) 有計算式 \(\begin{cases} \prod\limits_{i = 1} ^ m (c_i + 1) & k = 0 \\ \sum\limits_{i = 1} ^ m \frac{p_i ^ {(c_i + 1)k} - 1}{p_i - 1} & k > 0\end{cases}\)：根據乘法分配律，\(n\) 的所有約數的 \(k\) 次方之和可寫作 \(\prod\limits_{i = 1} ^ m\sum\limits_{j = 0} ^ {c_i} p_i ^ {jk}\)，等比數列求和後即得。
• 尤拉函數：\(\varphi(n) = \sum\limits_{i = 1} ^ n[i\perp n]\)，表示 \(n\) 以內與 \(n\) 互質的數的個數。關於尤拉函數的性質，詳見筆記 I.
• 本質不同質因子個數函數：\(\omega(n) = \sum\limits_{p \in \mathbb{P}} [p\mid n]\)，表示 \(n\) 的本質不同質因子個數。
• 莫比烏斯函數：\(\mu(n) = \begin{cases} 1 & n = 1 \\ 0 & \exists d > 1, d ^ 2\mid n \\ (-1) ^ {\omega(n)} & \mathrm{otherwise} \end{cases}\)。

以上所有函數除 \(\omega\) 是加性函數以外，其餘均為積性函數。根據計算式及積性函數的定義易證。

2. 素數篩法

素數篩法是數論體系中最基本的知識點，幾乎所有數論題目都需要篩出 \(1\sim n\) 的所有素數。

2.1 埃氏篩素數

埃氏篩用所有已經篩出的素數的倍數標記合數：從 \(2\) 到 \(n\) 列舉所有數 \(i\)，若 \(i\) 未被標記，則 \(i\) 是質數，將 \(i\) 除 \(i\) 以外的倍數標記為合數。

for(int i = 2; i < N; i++)
  if(!vis[i]) {
    pr[++cnt] = i;
    for(int j = 2 * i; j < N; j += i) vis[j] = 1;
  }

常數優化：根據合數 \(i\) 的最小質因子 \(\leq \sqrt i\)，可以從 \(i ^ 2\) 開始標記。

for(int i = 2; i < N; i++)
  if(!vis[i]) {
    pr[++cnt] = i;
    if(1ll * i * i < N) // 防止 i * i 溢位導致 RE
      for(int j = i * i; j < N; j += i) vis[j] = 1;
  }

埃氏篩的精髓在於其複雜度證明：不超過 \(n\) 的質數的倒數之和為 \(\mathcal{O}(\ln \ln n)\) 級別。

這說明埃氏篩的複雜度為 \(\mathcal{O}(n\ln \ln n)\)。

證明來自戴江齊學長：

因為每個數只會被其素因子篩到，所以 \(\sum\limits_{p\in \mathbb{P}, p\leq n} \dfrac 1 p = \sum\limits_{i = 1} ^ n \omega(i)\)。

根據 \(d(i)\) 的計算式，\(\sum\limits_{i = 1} ^ n 2 ^ {\omega(i)} \leq \sum\limits_{i = 1} ^ n d(i) = \mathcal{O}(n\ln n)\)。

根據 \(2 ^ x\) 的凸性和琴生不等式得 \(\sum\limits_{i = 1} ^ n 2 ^ {\omega(i)} \geq n 2 ^ {\frac{\sum_{i = 1} ^ n \omega(i)} n}\)，所以 \(2 ^ {\frac{\sum_{i = 1} ^ n \omega(i)} n} \leq \mathcal{O}(\ln n)\)。

兩邊同時取對數，\(\dfrac {\sum_{i = 1} ^ n \omega(i)} n \leq \mathcal{O}(\ln \ln n)\)，因此 \(\sum\limits_{i = 1} ^ n \omega(i)\leq \mathcal{O}(n\ln\ln n)\)。證畢。

2.2 線性篩素數

線性篩也稱尤拉篩，它和埃氏篩的思想類似。

埃氏篩的優秀之處在於僅用質數的倍數篩去合數，但合數會被多個質因子篩到。讓每個合數僅被篩一次就能做到線性。

考慮用每個合數的 最小質因子 篩去它：從 \(2\) 到 \(n\) 列舉所有數 \(i\)。對於每個 \(i\)，令其最小質因子為 \(p\)，則對於不大於 \(p\) 的質數 \(q\)，\(iq\) 的最小質因子為 \(q\)。將所有 \(iq\) 標記為合數，則每個合數 \(c\) 僅在 \(i = \dfrac c m\) 時以 \(im\) 的形式刪去，其中 \(m\) 是 \(c\) 的最小質因子。

綜上，有如下步驟：

• 從小到大遍歷當前篩出的所有素數 \(pr_j\)，將 \(i\times pr_j\) 標記為合數。
• 若 \(pr_j\mid i\)，退出迴圈。因為 \(pr_j\mid i\times pr_k(k > j)\)，所以 \(i\times pr_k\) 的最小質因子為 \(pr_j\) 不是 \(pr_k\)，再篩就重複了。

時間複雜度線性。模板題 P3383 程式碼如下：

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 1e8 + 5;
bool vis[N];
int n, q, pr[N / 16], cnt;
int main() {
  cin >> n;
  for(int i = 2; i <= n; i++) {
    if(!vis[i]) pr[++cnt] = i;
    for(int j = 1; j <= cnt && i * pr[j] <= n; j++) {
      vis[i * pr[j]] = 1;
      if(i % pr[j] == 0) break;
    }
  }
  cin >> q;
  while(q--) {
    int x;
    scanf("%d", &x);
    printf("%d\n", pr[x]);
  }
  return 0;
}

2.3 線性篩積性函數

線性篩提供了線上性時間內篩出具有特殊性質的積性函數在 \(1\sim n\) 處所有取值的基本框架。

只要積性函數 \(f\) 可在 \(\mathcal{O}(1)\) 時間內計算任意質數冪處的取值 \(f(p ^ k)\)，就適用線性篩。

• 注意，這只是 \(f\) 可線性篩的 充分但不必要 條件。存在更弱的條件使得 \(f\) 可線性篩但並不常見，如 \(\mathcal{O}(k)\) 計算 \(f(p ^ k)\)，這將在第三章介紹。

根據積性函數的性質，只要預先求出 \(low_i\) 表示 \(i\) 的最小質因子 \(p\) 的最高次冪 \(p ^ {v_p(i)}\)，對於 \(i\neq p ^ k\)，即可使用 \(f(low_i)f\left(\dfrac i {low_i}\right)\) 計算 \(f(i)\)。關於符號 \(v_p(n)\) 詳見筆記 I 基本定義與記號。

for(int i = 2; i < N; i++) {
  if(!vis[i]) pr[++pcnt] = i, f[i] = ..., low[i] = i; // 單獨算 f(p)
  for(int j = 1; j <= pcnt && i * pr[j] < N; j++) {
    vis[i * pr[j]] = 1;
    if(i % pr[j] == 0) { // i 與 p 不互質
      low[i * pr[j]] = low[i] * pr[j];
      if(i == low[i]) f[i * pr[j]] = ...; // i = p ^ k，單獨算 f(p ^ {k + 1})
      else f[i * pr[j]] = f[i / low[i]] * f[low[i * pr[j]]];
      break;
    }
   	low[i * pr[j]] = pr[j];
    f[i * pr[j]] = f[i] * f[pr[j]]; // i 與 p 互質，f(ip) = f(i)f(p) 
  }
}

3. 狄利克雷折積

狄利克雷（Dirichlet）折積是數論函數的基本運算，其重要程度相當於代數中的四則運算。

3.1 定義與性質

為數列定義折積，自然想到加法折積 \(c_k = \sum\limits_{i + j = k} a_ib_j\)，但加法折積不能保留積性。讓我們發散想象力，如果將加法換成乘法，結果如何？這引出了 狄利克雷折積：

上式簡記為 \(h = f * g\)。按照定義式計算狄利克雷折積，複雜度為調和級數的 \(\mathcal{O}(n\ln n)\)。

接下來證明一些狄利克雷折積的性質。

性質 1：狄利克雷折積具有 交換律，結合律，分配律。

交換律：

其中 \(d' = \dfrac n d\)。因此 \(f * g = g * f\)。

結合律：

其中 \(k = \dfrac d i\)。因此 \((f * g) * h = f * (g * h)\)。

分配律：

因此 \((f + g) * h = f * h + g * h\)。證畢。

性質 2：\(\epsilon * f = f\)。

證明：\((\epsilon * f)(n) = \sum\limits_{d \mid n}[d = 1]f\left(\dfrac n d\right) = f(n)\)。證畢。

因此單位函數 \(\epsilon\) 為狄利克雷折積的 單位元。

既然存在單位元，就可以據此定義數論函數 \(f\) 的逆元 \(f ^ {-1}\)，滿足 \(f * f ^ {-1} = \epsilon\)。

性質 3：\(f\) 可逆當且僅當 \(f(1)\neq 0\)。

證明：設 \(g = f ^ {-1}\)。當 \(f(1) = 0\) 時，\(f(1)g(1) = 0\) 且 \(f(1) g(1) = \epsilon(1) = 1\)，矛盾。當 \(f(1) \neq 0\) 時，\(g(1) = \dfrac 1 {f(1)}\)，對 \(n > 1\) 的 \(g(x)\) 通

過 \(\sum\limits_{d\mid x} g(d)f\left(\dfrac n d\right) = 0\) 得到遞推式 \(g(n) = -\dfrac{\sum\limits_{d \mid n, d \neq n} g(d)f\left(\dfrac n d\right)} {f(1)}\)。這同時說明 逆元唯一。證畢。

性質 4：\(f = g\) 的充要條件是 \(f * h = g * h\)，其中 \(h(1) \neq 0\)。

證明：\(f * h = g * h\Rightarrow f * h * h ^ {-1} = g * h * h ^ {-1} \Rightarrow f = g\)，充分性得證。必要性顯然。證畢。

性質 5：積性函數的狄利克雷折積是積性函數。

證明：考慮積性函數 \(f\) 和 \(g\) 的狄利克雷折積 \(h\)。若 \(a\perp b\)，則

其中 \(d = d_1d_2\)。第二步依賴於 \(f\) 和 \(g\) 的積性：\(f(d_1) f(d_2) = f(d_1d_2) = f(d)\)。證畢。

性質 6：積性函數的逆元是積性函數。

證明：設 \(g = f ^ {-1}\)。根據 \(f\) 的積性可知 \(g(1) = \dfrac 1 {f(1)} = 1\)，所以 \(g(n) = g(1) g(n)\)。

考慮歸納法。對於 \(n, m > 1\) 且 \(n\perp m\)，假設對於任意 \(xy < nm\) 且 \(x\perp y\) 均有 \(g(xy) = g(x)g(y)\)。因 \(n = 1\) 或 \(m = 1\) 時命題成立，只需證明 \(g(nm) = g(n)g(m)\)。

因為 \(n, m > 1\)，所以 \(\epsilon(n) = \epsilon(m) = 0\)，所以 \(g(nm) = g(n)g(m)\)。證畢。

綜合性質 5 和性質 6，兩個積性函數的積與商都是積性函數。注意，積性函數的和與差不是積性函數。

3.2 線性篩 Dirichlet 折積

根據積性函數的狄利克雷折積是積性函數這一結論，我們嘗試線上性時間內篩出 \(h = f * g\)。

寫出 \(h\) 的表示式，有

對於第一和第三種情況，線性篩時可以總代價 \(\mathcal{O}(n)\) 求出。關鍵在於 Case 2，若 \(f\) 和 \(g\) 在質數冪處的取值已經求出，則需要 \(\mathcal{O}(k)\) 的時間計算。

• 特別的，當 \(f\) 為完全積性函數時，\(h(p ^ k)\) 可以寫作 \(f(p)h(p ^ {k - 1}) + g(p ^ k)\)，可以 \(\mathcal{O}(1)\) 方便地計算。對於 \(g\) 同理。

嘗試估計第二部分的複雜度。考慮到所有小於 \(\leq \sqrt[k]n\) 的質數會對複雜度產生 \(\mathcal{O}(k)\) 的貢獻，因此

感性理解，\(x ^ 2 \sqrt[x]{n}\) 隨著 \(n\) 增大，\(x\) 增大時 \(x ^ 2\) 一項增大的速度遠小於 \(\sqrt[x]{n}\) 衰減的速度。從這一點入手，考慮證明 \(x ^ 2 \sqrt[x] n \leq \mathcal{O}(n)\)。

當 \(x = 1\) 時顯然成立，否則考慮 \(x\in [2, \log_2 n]\) 時 \(x ^ 2\) 的最大值 \(\log_2 ^ 2 n\) 與 \(\sqrt[x] n\) 的最大值 \(\sqrt n\) 之積，因為當 \(x\to +\infty\) 時 \(\log_2 x\) 是 \(\sqrt x\) 的高階無窮小，所以 \(\mathcal{O}(\sqrt n\log ^ 2 n) \leq \mathcal{O}(n)\)。

因此，\(T(n) \leq \dfrac 1 {\ln n} \sum\limits_{i = 1} ^ {\log_2 n} \mathcal{O}(n) = \mathcal{O}(n)\)。

綜上，使用線性篩求出兩個在質數冪處取值已知的積性函數的狄利克雷折積在 \(1\sim n\) 處的取值的時間複雜度為 \(\mathcal{O}(n)\)。

我們得到了積性函數可線性篩的更弱的條件：可以 \(\mathcal{O}(k)\) 時間計算質數冪處的取值。

3.3 狄利克雷字首和

前置知識：高維字首和。

任意數論函數 \(f\) 卷常數函數 \(1\) 等價於對 \(f\) 做 狄利克雷字首和：令 \(g = f * 1\)，則 \(g(n) = \sum\limits_{d\mid n} f(d)\)。

對每個 \(n\) 計算給定數論函數在其所有因數處的取值之和有很好的實際含義，因此狄利克雷字首和是比較重要的演演算法。

將每個數 \(n\) 寫成無窮序列 \(a_n = \{c_1, c_2, \cdots, c_i, \cdots\}\) 表示 \(n = \prod p_i ^ {c_i}\)，其中 \(p_i\) 表示第 \(i\) 個質數。因為 \(x\mid y\) 的充要條件為 \(a_x(c_i) \leq a_y(c_i)\)，所以 \(f * 1\) 可以看成對下標做關於其無窮序列的高維字首和，即 \(g(n) = \sum\limits_{\forall i, a_d(c_i) \leq a_n(c_i)} f(d)\)。

根據高維字首和的求法，列舉每一維並將所有下標關於該維做字首和，可得狄利克雷字首和的實現方法：初始令 \(x_i = f(i)\)。從小到大列舉每個質數 \(p_i\)，列舉 \(k\)，將 \(x_{p_ik}\) 加上 \(x_k\)，相當於 \(k\) 貢獻到給 \(a_k(i)\) 加上 \(1\) 之後的下標。最終得到的 \(x\) 即為 \(g\)。

根據小於 \(n\) 的素數倒數之和為 \(\ln\ln n\) 這一結論，狄利克雷字首和的時間複雜度為 \(\mathcal{O}(n\ln\ln n)\)。

模板題 P5495 程式碼。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e7 + 5;
int n;
unsigned ans, a[N], seed;
inline unsigned rd() {
  seed ^= seed << 13, seed ^= seed >> 17, seed ^= seed << 5;
  return seed;
}
bool vis[N];
int cnt, pr[N >> 3];
void sieve() {
  for(int i = 2; i <= n; i++) {
    if(!vis[i]) pr[++cnt] = i;
    for(int j = 1; j <= cnt && i * pr[j] <= n; j++) {
      vis[i * pr[j]] = 1;
      if(i % pr[j] == 0) break;
    }
  }
}
int main() {
  cin >> n >> seed, sieve();
  for(int i = 1; i <= n; i++) a[i] = rd();
  for(int i = 1; i <= cnt; i++)
    for(int j = 1; j * pr[i] <= n; j++)
      a[j * pr[i]] += a[j];
  for(int i = 1; i <= n; i++) ans ^= a[i];
  cout << ans << endl;
  return 0;
}

4. 數論分塊

數論分塊又稱整除分塊，因其解決的問題與整除密切相關而得名。數論分塊用於求解形如

的和式。前提為 \(f\) 的字首和可快速計算。

感性認知：使得 \(\left\lfloor\dfrac n x\right\rfloor = k\) 的正整數 \(x\) 的範圍為 \(\left(\left\lfloor \dfrac n {k + 1}\right\rfloor, \left\lfloor \dfrac n k\right\rfloor \right]\)。

4.1 演演算法介紹

如果 \(\left\lfloor\dfrac n i\right\rfloor\) 的數量不多，可以考慮轉換貢獻形式，將原式寫成若干 \(g\left(\left\lfloor\dfrac n i\right\rfloor\right)\) 乘以一段 \(f\) 的和。接下來分析不同 \(\left\lfloor\dfrac n i\right\rfloor\) 的數量的上界。

當 \(i\) 較大時，\(\left\lfloor \dfrac {n} {i} \right\rfloor\) 被限制在較小範圍內，很多 \(\left\lfloor \dfrac {n} {i}\right\rfloor\) 均相同。結合 \(\min\left(i, \dfrac n i\right) \le \sqrt n\)，可以想到根號分治。

結論 1：對於任意 \(i\in [1, n], n\in \mathbb N_+\)，不同的 \(\left\lfloor \dfrac {n} {i}\right\rfloor\) 至多 \(2\sqrt n\) 個。

證明：\(i \leq \sqrt n\) 時，\(\left\lfloor \dfrac {n} {i}\right\rfloor\) 只有 \(\sqrt n\) 個；\(i > \sqrt n\) 時，\(\left\lfloor \dfrac {n} {i}\right\rfloor \leq \sqrt n\)，只有 \(\sqrt n\) 個。證畢。

根據結論 1，列舉 \(\mathcal{O}(\sqrt n)\) 種整除值 \(d\)，求出最小和最大的 \(i\) 使得 \(\left\lfloor\dfrac n i\right\rfloor = d\)，分別記作 \(l, r\)，則原式可寫為 \(\sum\limits_{d} g(d)\sum\limits_{i = l} ^ r f(i)\)。因此，只要 \(f\) 的字首和可以快速計算，\(g\) 在某處的取值可以快速得到，即可在 \(\mathcal{O}(\sqrt n)\) 的時間內解決原問題。

這樣，問題轉化為求使得 \(\left\lfloor\dfrac n i\right\rfloor = d\) 的最小和最大的 \(i\)。

\(\left\lfloor\dfrac n i\right\rfloor = d\) 對 \(i\) 有兩條限制，分別為 \(i(d + 1) > n\) 和 \(id \leq n\)。因為使得 \(id\leq n\) 的最大的 \(i\) 就是 \(\left\lfloor\dfrac n d\right\rfloor\)，同理使得 \(i(d + 1) \leq n\) 的最大的 \(i\) 為 \(\left\lfloor\dfrac n {d + 1}\right\rfloor\)，所以 \(l = \left\lfloor\dfrac n {d + 1}\right\rfloor + 1\)，\(r = \left\lfloor\dfrac n d\right\rfloor\)。

如何不重不漏地列舉所有整除值？沒有必要。我們只需依次列舉每個 \(i\)，並藉助上述工具跳過 \(\left\lfloor\dfrac n i\right\rfloor\) 相同的極長連續段即可。

具體地，令當前列舉到的 \(i\) 為 \(l\)，此時整除值為 \(d = \left\lfloor\dfrac n i\right\rfloor\)。因為使得 \(\left\lfloor\dfrac n i\right\rfloor = d\) 的最大的 \(i\) 等於 \(\left\lfloor\dfrac n d\right\rfloor\)，所以令 \(r = \left\lfloor\dfrac n {\left\lfloor\frac n l\right\rfloor}\right\rfloor\)，將 \(g(d)(s(r) - s(l - 1))\) 累和入答案，並令 \(l \gets r + 1\) 表示跳過 \(l + 1\sim r\) 這一段 \(i\)，若 \(l > n\) 則退出。其中 \(s\) 是 \(f\) 的字首和。

每個整除值僅會被遍歷一次，時間複雜度 \(\mathcal{O}(\sqrt n)\)。

• 注意，當 \(i\) 的上界不等於 \(n\) 時，設其為 \(m\)，則 \(r\) 應與 \(m\) 取較小值（處理 \(n > m\) 的情況），且當 \(\left\lfloor\dfrac n i\right\rfloor = 0\) 時需要特判，直接令 \(r\) 等於 \(m\)（處理 \(n < m\) 的情況）。

4.2 擴充套件

4.2.1 向上取整

嘗試將向下取整變為向上取整。

對於左邊界 \(l\)，求出使得 \(\left\lceil\dfrac n l \right\rceil = \left\lceil\dfrac n r \right\rceil\) 的最大的 \(r\)。不妨設 \(k = \left\lceil\dfrac n l\right\rceil\)，則

第三步轉換是因為 \(n, k\) 均為正整數。因此，只需令 \(r\gets \left\lfloor\dfrac{n - 1}{\left\lceil\frac n l\right\rceil - 1}\right\rfloor\) 即可。

注意特判 \(\left\lceil\dfrac n l\right\rceil=1\)，此時 \(r\) 的上界為無窮大，需要取實際上界。

4.2.2 高維數論分塊

當和式中出現若干下取整，形如

時，只需稍作修改，令 \(r = \min\limits_{j = 1} ^ c\left(\left\lfloor \dfrac {n_j} {\left\lfloor \frac {n_j} l\right\rfloor}\right\rfloor\right)\) 即可。不要忘記對 \(n\) 取 \(\min\)。

時間複雜度為 \(\sum \sqrt {n_j}\)。將使得存在 \(n_j\) 滿足 \(\left\lfloor \dfrac {n_j} {i}\right\rfloor \neq \left\lfloor \dfrac {n_j} {i + 1}\right\rfloor\) 的位置 \(i\) 視作斷點，則總斷點數量為每個下取整式的端點數量相加而非相乘。我們只會在每相鄰兩個斷點形成的區間處遍歷一次，故有該時間複雜度。

4.3 例題

I. [模擬賽] 你還沒有解除安裝嗎

給定 \(A_1, B_1, A_2, B_2, N\)，求有多少 \(x\in [1, N]\) 使得 \(B_1 + \left\lfloor\dfrac{A_1}{x}\right\rfloor = B_2 + \left\lfloor\dfrac{A_2}{x}\right\rfloor\)。\(T\leq 2\times 10 ^ 3\)，其他所有數 \(\in [1, 10 ^ 8]\)。時限 1s。

考慮數論分塊 \([l, r]\) 固定 \(\dfrac{A_1} x\)，解出 \(d = \dfrac{A_2}{x}\)，反推出合法的 \(x\) 的範圍：\([l, r] \cap \left[\dfrac{A_2}{d + 1} + 1, \dfrac{A_2}{d}\right]\)。時間複雜度 \(\mathcal{O}(T\sqrt V)\)。

另一種方法是直接二維數論分塊。細節更少，且時間複雜度相同。

#include <bits/stdc++.h>
using namespace std;
int T, a1, b1, a2, b2, n;
int main() {
	cin >> T;
	while(T--) {
		int ans = 0;
		cin >> a1 >> b1 >> a2 >> b2 >> n;
		for(int l = 1, r = 1; l <= n; l = r + 1) {
			r = min(n, min(a1 / l ? a1 / (a1 / l) : n, a2 / l ? a2 / (a2 / l) : n));
			if(b1 + a1 / l == b2 + a2 / l) ans += r - l + 1;
		}
		cout << ans << endl;
	}
	return 0;
}

*II. CF1603C Extreme Extension

數論分塊優化 DP。

一個數如何分裂由後面分裂出來的數的最小值決定，顯然貪心使分出來的數儘量均勻，例如若 \(9\) 要裂成若干個比 \(4\) 小的數，那麼 \(3, 3, 3\) 比 \(2, 3, 4\) 更優。

從後往前考慮，對於每個數 \(a_i\) 和值 \(j\in [1, a_i]\)，求出有多少以 \(a_i\) 開頭的子串根據上述貪心策略分裂出的最小值為 \(j\)，\(j\) 由 \(a_i\) 分裂零次或若干次得到，記為 \(f_{i, j}\)。

首先明確兩點：

• \(a_i\) 分裂成若干 \(\leq v\) 的數，最少分裂次數為 \(\left\lceil \dfrac {a_i} v \right\rceil - 1\)，分裂成 \(\left\lceil \dfrac {a_i} v \right\rceil\) 個數。
• \(a_i\) 分裂成 \(v\) 個數，這些數最小值的最大值為 \(\left\lfloor \dfrac {a_i} v \right\rfloor\)。

考慮轉移。

注意到對於固定的分裂次數，分裂出的值也是確定的。考慮列舉使得分裂次數相同的區間 \([l, r]\)，即 \(a_i\) 整除 \([l, r]\) 內所有數向上取整的結果相同，可以通過向上取整的數論分塊實現。

令 \(c = \left\lceil \dfrac {a_i} l \right\rceil\) 表示分裂出的數的個數，則分裂出的數的最小值為 \(v = \left\lfloor \dfrac {a_i} c \right\rfloor\)。因此，\(\sum\limits_{j = l} ^ r f_{i + 1, j}\) 轉移到 \(f_{i, v}\)。

考慮在每個位置處統計該位置在所有子段中總分裂次數之和，則答案加上 \(i\times (c - 1) \times f_{i , v}\)。其含義為，共有 \(f_{i, v}\) 個子段使得 \(a_i\) 要分裂出 \(c\) 個數，即分裂 \(c - 1\) 次。同時，若子段 \([i, k]\) 在 \(i\) 處分裂 \(c - 1\) 次，則對於任意子段 \([x, k]\) 滿足 \(1\leq x\leq i\)，\(a_i\) 分裂的次數都是 \(c - 1\)，因為 \(a_i\) 的分裂不受前面的數的影響。

注意，當 \(c = 1\) 時，\(f_{i, v}\) 即 \(f_{i, a_i}\) 需要加上 \(1\)，表示新增以 \(a_i\) 結尾的子段。

用 vector 儲存所有 \(f_i\) 並轉移，時間複雜度 \(\mathcal{O}(n\sqrt {a_i})\)。捲動陣列優化後空間複雜度 \(\mathcal{O}(n)\)。程式碼。

III. P2260 [清華集訓2012] 模積和

求 \(\sum\limits_{i = 1} ^ n n \bmod i\) 是經典問題：拆成 \(\sum\limits_{i = 1} ^ n \left(n - \left\lfloor\dfrac n i\right\rfloor i\right)\) 後數論分塊，時間複雜度 \(\mathcal{O}(\sqrt n)\)。

原式可寫作

全部使用數論分塊解決。可能需要的公式：\(\sum\limits_{i = 1} ^ ni ^ 2 = \dfrac{n(n + 1)(2n + 1)} 6\)。

時間複雜度 \(\mathcal{O}(\sqrt n)\)，程式碼。

*IV. P3579 [POI2014] PAN-Solar Panels

非常不錯的題目。

當 \(\lfloor\frac {a - 1} k\rfloor < \lfloor\frac b k\rfloor\) 且 \(\lfloor\frac{c - 1} k\rfloor < \lfloor\frac d k\rfloor\) 時，\([a, b]\) 和 \([c, d]\) 均含有 \(k\) 的倍數。答案為所有這樣的 \(k\) 的最大值。

我們當然可以四維數論分塊，但注意到在使得 \(\lfloor\frac b k \rfloor\) 相同且 \(\lfloor \frac d k\rfloor\) 相同的 \(k\) 的區間 \([l, r]\) 當中，選擇 \(k = r\) 可以使 \(\lfloor \frac{a - 1} k\rfloor\) 和 \(\lfloor \frac {c - 1} k\rfloor\) 儘可能小，更有機會滿足要求。也就是說，若 \(k = r\) 都不滿足條件，則 \(l\leq k \leq r\) 均不滿足條件。因此二維數論分塊即可。

時間複雜度 \(\mathcal{O}(T\sqrt V)\)，程式碼。

5. 莫比烏斯函數

前置知識：容斥原理。

到達數論最高城，莫比烏斯反演！太好用啦莫反，哎呀這不 GCD 麼，還是列舉倍數吧家人們。

5.1 引入

觀察 \(\mu(n)\) 的定義式 \(\begin{cases} 1 & n = 1 \\ 0 & \exists d > 1, d ^ 2\mid n \\ (-1) ^ {\omega(n)} & \mathrm{otherwise} \end{cases}\)，讀者也許會好奇數學家為什麼要定義如此奇怪的函數。這背後必然隱藏著其某種神祕而重要的性質。

\(g(n) = \sum\limits_{d\mid n} f(d)\) 的狄利克雷字首和形式相當常見，因此根據 \(g\) 求原函數 \(f\) 也很重要。因為 \(g = f * 1\)，所以 \(f = g * 1 ^ {-1}\)。

設 \(h = 1 ^ {-1}\)，根據逆元遞推式推導 \(h\) 的一般形式。先將遞推式寫出，\(h(n) = -\sum\limits_{d\mid n, d\neq n} h(d)\)。

由於積性函數的逆元具有積性，所以 \(h\) 具有積性。只需觀察 \(h\) 在質數冪 \(p ^ k\) 處的取值即可得到一般化的結論。

• \(h(p) = -h(1) = -1\)。
• \(h(p ^ 2) = -(h(1) + h(p)) = 0\)。
• \(h(p ^ 3) = -(h(1) + h(p) + h(p ^ 2)) = 0\)。

據此，可歸納證明 \(h(p ^ k)\) 當 \(k = 0\) 時等於 \(1\)，\(k = 1\) 時等於 \(-1\)，\(k \geq 2\) 時等於 \(0\)。

考慮 \(n = \prod\limits_{i = 1} ^ m p_i ^ {c_i}\)。根據 \(h\) 的積性，若存在 \(c_i\geq 2\) 則 \(h(n) = 0\)，否則 \(h(n)\) 等於 \((-1) ^ m\)。容易發現這與莫比烏斯函數的定義式相符。因此 \(1 ^ {-1} = \mu\)，即

驗證：令 \(S(n) = \sum\limits_{d\mid n} \mu(d)\)。考慮 \(n\) 的所有質因子 \(p_1 \sim p_m\)。對於任意 \(k\) 個質因子的乘積 \(P\)，它產生 \(\mu(P) = (-1) ^ k\) 的貢獻。因此，\(S(n)\) 可寫作 \(\sum\limits_{i = 0} ^ m (-1) ^ i\dbinom m i = (1 - 1) ^ m\)。當 \(m = 0\) 時，\(n = 1\)，\(S(n)\) 顯然為 \(1\)。否則 \(S(n) = 0 ^ m = 0\)。這從另一個角度說明了 \(\mu * 1 = \epsilon\)。

也可以從容斥係數的角度理解莫比烏斯函數。設 \(g(n) = \sum\limits_{n\mid d} f(d)\)，即 \(g(n)\) 是 \(f\) 在所有 \(n\) 的倍數處的取值和。現在已知 \(g\)，要求 \(f(1)\)。則 \(f(1)\) 等於 \(f\) 在 \(1\) 的倍數處的取值和，減去在質數處的取值和，但是多減去了在兩個不同質數乘積處的取值和，因此要加上這些值，但是多加上了在三個不同質數乘積處的取值和，以此類推。因此，若 \(n\) 為 \(k\) 個不同質數的乘積，則 \(f(1)\) 會受到 \(g(n)\) 係數為 \((-1) ^ k\) 的貢獻，如下圖，圖源。

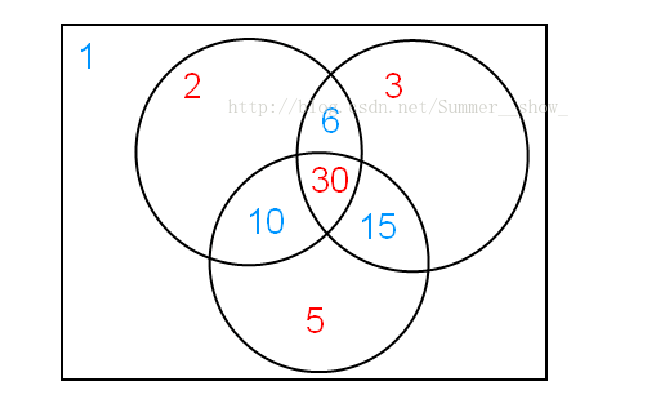
換言之，對 \(\pmb {\mathbb N}\) 做容斥原理，得到貢獻係數 \(\boldsymbol \mu\)。

5.2 篩

據定義，線性篩莫比烏斯反演是容易的。

int vis[N], cnt, pr[N], mu[N];
void sieve() {
  mu[1] = 1;
  for(int i = 2; i < N; i++) {
    if(!vis[i]) pr[++cnt] = i, mu[i] = -1;
    for(int j = 1; j <= cnt && i * pr[j] < N; j++) {
      vis[i * pr[j]] = 1;
      if(i % pr[j] == 0) break; // 此時 i * pr[j] 含至少兩個 pr[j]，mu = 0
      mu[i * pr[j]] = -mu[i]; // mu[i * pr[j]] = mu[i] * mu[pr[j]] = -mu[i]
    }
  }
}

當時間複雜度可接受時，根據 \(\mu\) 的狄利克雷折積求逆式 \(\mathcal{O}(n\log n)\) 遞推更方便。

int mu[N];
void sieve() {
  mu[1] = 1;
  for(int i = 1; i < N; i++)
    for(int j = i + i; j < N; j += i)
      mu[j] -= mu[i];
}

5.3 莫比烏斯反演

\(\mu * 1 = \epsilon\) 引出了 \(\mu\) 的關鍵性質：\([n = 1] = \epsilon(n) = \sum\limits_{d\mid n} \mu(d)\)。這使得我們可以用 \(\mu\) 的和式代替形如 \([n = 1]\) 的艾佛森括號，體現出其核心 「反演」。

• 用和式代替判斷式往往重要但不直觀，所以初學者難以理解 OI 常見反演技巧。例如，對於奇質數 \(p\) 有 \(\sum\limits_{x = 1} ^ {p - 1} [x ^ 2 = a] = \left(\dfrac a p\right) + 1 = (a ^ {\frac{p - 1} 2} \bmod p) + 1\)；單位根反演 \([n\mid a] = \dfrac 1 n\sum\limits_{i = 0} ^ {n - 1} \omega_n ^ {ia}\)。從判斷式到和式的過程形成套路，深入瞭解其背後的邏輯有助於讀者掌握並熟練運用這種套路。

莫比烏斯反演的結論：

• 若 \(g(n) = \sum\limits_{d\mid n} f(d)\)，則 \(f(n) = \sum\limits_{d\mid n} \mu(d) f\left(\dfrac n d\right)\)。即若 \(g = f * 1\)，則 \(f = g * \mu\)。
• 若 \(g(n) = \sum\limits_{n\mid d} f(d)\)，則 \(f(n) = \sum\limits_{n\mid d} \mu\left(\dfrac d n\right) g(d)\)。這其實就是上一節末尾提到的 \(\mu\) 作為容斥係數。驗證：\(\sum\limits_{n\mid d} \mu\left(\dfrac d n\right) \sum\limits_{d\mid k} f(k) = \sum\limits_{n\mid k} f(k) \sum\limits_{d\mid \frac k n} \mu(d) = f(n)\)。
• 因為 \(\varphi * 1 = \mathrm{id}\)，所以 \(\mathrm{id} * \mu = \varphi\)，即 \(\sum\limits_{d \mid n} \dfrac n d \mu(d) = \varphi(n)\)。變式為 \(\sum\limits_{d\mid n} \dfrac{\mu(d)} d = \dfrac {\varphi(n)} n\)。

莫比烏斯反演的常見應用：

別看它只是將 \(\gcd(i, j)\) 帶入 \(n\)，但這一步將 「\(i, j\) 互質」 這個條件轉化為列舉 \(\gcd(i, j)\) 的約數 \(d\)，然後對 \(\mu(d)\) 求和。在 \(i, j\) 同樣需要列舉的時候，可以先列舉 \(d\) 並計算合法的 \((i, j)\) 對數，這樣 \(i, j\) 合法當且僅當 \(d\mid i\) 且 \(d\mid j\)，就把 \(i, j\) 獨立開了。

5.4 常見技巧

相當於對 「最大公約數為 \(d\) 的倍數」 中的 \(d\) 做容斥：加上最大約數為 \(1\) 的倍數的對數，減去最大公約數為 \(p_i\) 的倍數的對數，加上最大公約數為 \(p_ip_j(i \neq j)\) 的倍數的對數，以此類推，得到每個 \(d\) 的貢獻係數即莫比烏斯函數。

考慮單個質因子 \(p\)，再用中國剩餘定理合併。設 \(a = v_p(i)\) 即 \(i\) 含質因子 \(p\) 的數量，\(b = v_p(j)\)，則 \(v_p(ij) = a + b\)。對於 \(ij\) 的約數 \(d\)，若 \(v_p(d) \leq a\)，則令其對應 \(v_p(x) = v_p(d)\)，\(v_p(y) = 0\)；若 \(v_p(d) > a\)，則令其對應 \(v_p(x) = 0\)，\(v_p(y) = v_p(d) - a\)。容易發現互質對 \((x, y)\) 和 \(d\) 之間形成雙射，因此對 \(d\) 計數相當於對 \([x\perp y]\) 計數。例 XII.

5.5 例題

讓我們在例題中感受莫比烏斯反演的廣泛應用。除特殊說明，以下所有分式均向下取整。

I. P2522 [HAOI2011] Problem b

二維差分將和式下界化為 \(1\)，然後推式子：

只有 \(k\) 的倍數有用，將和式縮放 \(k\) 倍，得

莫比烏斯反演，得

列舉約數 \(d\)，記 \(c = \min\left(\dfrac n k, \dfrac m k\right)\)，

由於 \(1\sim x\) 中 \(y\) 的倍數有 \(\dfrac x y\) 個，故原式簡化為

整除分塊即可，時間複雜度 \(\mathcal{O}(n + T\sqrt n)\)，注意非必要不開 long long。程式碼。

II. SP5971 LCMSUM - LCM Sum

設 \(F(n)\) 表示 \(n\) 以內所有與 \(n\) 互質的數的和。當 \(n \geq 2\) 時，因為若 \(x\perp n\) 則 \(n - x\perp n\)，所以與 \(n\) 互質的數成對出現且和為 \(n\)。也就是說，每個與 \(n\) 互質的數對 \(F(n)\) 的平均貢獻是 \(\dfrac n 2\)。因此 \(F(n) = \dfrac{n\varphi(n)} 2\)。

當 \(n = 1\) 時，\(F(1)\) 顯然為 \(1\)。

另一種推導 \(F\) 的方式是莫比烏斯反演：

最後一步是因為 \(\mu * \mathrm{id} = \varphi\)，\(\mu * 1 = \epsilon\)。

答案為 \(n\sum\limits_{d\mid n} F(d)\)，化簡為 \(\dfrac n 2 \left(1 + \sum\limits_{d\mid n} d \varphi(d)\right)\)。線性篩出 \(1 * (\mathrm{id} \times \varphi)\) 即可做到 \(\mathcal{O}(T + n)\)。程式碼。

III. P4318 完全平方數

設 \(f(n)\) 表示 \([1, n]\) 當中非完全平方數倍數的數的個數。二分答案，找到最小的 \(r\) 使得 \(f(r) \geq K\)，則 \(r\) 即為所求。

首先去掉 \(4, 9, \cdots, p ^ 2\) 的倍數，但同時是其中兩個數的倍數的數會被算兩次，所以加上 \((p_1p_2) ^ 2\) 的倍數，依次類推。相當於對 \(\mathbb N\) 做容斥，自然想到莫比烏斯函數。因此

直接計算，時間複雜度 \(\mathcal{O}(\sqrt n \log n)\)。程式碼。

IV. P2257 YY 的 GCD

注意到分母上的 \(pd \) 與兩個變數相關，很麻煩。不妨設 \(T = pd\)，得

這一步調整了計算順序使得可通過乘法分配律提出向下取整的式子。

另一種推導方式：考慮對 \([\gcd(i, j) = p]\) 容斥，然後對所有質數 \(p\) 求和，可知貢獻係數 \(f\) 為所有容斥係數之和，即 \(f = \sum\limits_{p\in \mathbb P} \mu * \epsilon_p(n)\)。換句話說，\(f\) 等於將 \(\mu\) 的 下標 擴大質數倍後求和。我們發現 \(f(T) = \sum\limits_{p \mid T\land p\in \mathbb P} \mu\left(\dfrac T p\right)\)，與上式等價。

\(f\) 可以類似埃氏篩 \(n\log\log n\) 求出，因為每個位置僅與其所有質因子有關。將 \(f\) 字首和後整除分塊即可。時間複雜度 \(\mathcal{O}(T\sqrt n + n \log\log n)\)。

儘管 \(f\) 不是積性函數，但 \(f(T)\) 可以線性篩。具體方式留給讀者自行推導，時間複雜度 \(\mathcal{O}(T\sqrt n+n)\)。程式碼。

V. P3455 [POI2007] ZAP-Queries

P2522 的子問題，程式碼。

VI. P2568 GCD

P2257 的子問題。

VII. P1829 [國家集訓隊] Crash 的數位表格

設 \(c = \min(n, m)\)。

根據 \(ij = \gcd(i, j) \times \mathrm{lcm}(i, j)\) 列舉 \(d = \gcd(i, j)\)，得

莫比烏斯反演，得

注意到後面兩個和式不太好化簡，我們設 \(S(T) = \sum\limits_{i = 1} ^ {\frac n T}\sum\limits_{j = 1} ^ \frac m T ij\)，並令 \(T = de\)，交換列舉順序，得

至此已經可以狄利克雷字首和 \(c\log \log c\) 求解問題。但注意到 \(\mu \cdot \mathrm{id}\) 是積性函數，所以 \(f = 1 * (\mu \cdot \mathrm{id})\) 也是積性函數，且其在質數冪處的取值可快速計算，可線性篩。則答案式化簡為 \(\sum\limits_{i = 1} ^ c S(i)f(i)i\)，其中僅 \(S\) 與 \(n, m\) 有關。同時注意到 \(S\) 僅涉及到 \(n, m\) 整除值處的等差數列求和，因此求出 \(f(i) i\) 的字首和後，可整除分塊 \(\mathrm{O}(\sqrt c)\) 求解答案。

時間複雜度 \(\mathcal{O}(c + T\sqrt c)\)。程式碼。

VIII. AT5200 [AGC038C] LCMs

令 \(S = \sum\limits_{i = 1} ^ N \sum\limits_{j = 1} ^ N \mathrm{lcm}(A_i, A_j)\)，則答案為 \(S\) 減去 \(A\) 的和之後除以 \(2\)。問題轉化為求 \(S\)。

設 \(c_i\) 表示 \(i\) 在 \(A\) 中的出現次數，即 \(c_i = \sum\limits_{j = 1} ^ N [A_j = i]\)，則

其中 \(T = dd'\)，\(f(T) = \sum\limits_{d\mid T} \mu(d) d\)，\(g(T) = \sum\limits_{i = 1} ^ {\frac V T} ic_{iT}\)。\(f\) 容易線性篩預處理，\(g\) 可以列舉因數或狄利克雷字尾和。時間複雜度 \(\mathcal{O}(V\log V)\) 或 \(\mathcal{O}(V\log\log V)\)。程式碼。

IX. P3911 最小公倍數之和

雙倍經驗。

X. P6156 簡單題

和上題一樣的套路。列舉 \(\gcd\)，再莫比烏斯反演，得

令 \(T = dd'\)，得

線性篩預處理出 \(f = (d\times \mu ^ 2) * \mu\) 的字首和，並預處理自然數冪和求後面的東西。整除分塊求解上式，時間複雜度 \(\mathcal{O}(n\frac {\log k}{\log n})\)。程式碼見下一題。

XI. P6222 「P6156 簡單題」加強版

雙倍經驗，時間複雜度 \(\mathcal{O}(n\frac {\log k}{\log n} + T\sqrt n)\)。注意比較卡空間。程式碼。

XII. P3327 [SDOI2015] 約數個數和

利用 5.4 小節的第二個公式，套入莫比烏斯反演，可得答案式

整除分塊預處理 \(g(n) = \sum\limits_{i = 1} ^ n \dfrac n i\)，則答案為 \(\sum\limits_{d = 1} ^ {\min(n, m)} \mu(d) g(\frac n d) g(\frac m d)\)，整除分塊即可。時間複雜度 \(\mathcal{O}((n + T)\sqrt n)\)。程式碼。

XIII. P1447 [NOI2010] 能量採集

XIV. P6810 「MCOI-02」Convex Hull 凸包

XV. P2158 [SDOI2008] 儀仗隊

XVI. P3704 [SDOI2017] 數位表格

設 \(c = \min(n, m)\)。

線性或線對預處理 \(f\) 及其逆元，線對預處理 \(g(n) = \sum\limits_{d\mid n} f_d ^ {\mu(\frac n d)}\)。對每組詢問整除分塊即可做到 \(\mathcal{O}(T\sqrt n\log n)\)。

6. 杜教篩

杜教篩可以在亞線性時間內求出滿足條件的數論函數字首和。

6.1 演演算法介紹

杜教篩公式的推導相當自然，但動機十分巧妙。設希望求出 \(f\) 在 \(n\) 處的字首和 \(s(n) = \sum\limits_{i = 1} ^ n f(i)\)，我們構造另一個數論函數 \(g\)，設 \(h = f * g\)，則

這說明若 \(g, h\) 的字首和可快速求出，我們就得到了 \(s(n)\) 關於其所有整除值處取值的遞推式，即

一般可杜教篩函數 \(f\) 及其對應建構函式 \(g\) 均為積性函數，因此 \(g(1) = 1\)，公式又寫為。

另一種理解方式：設第一象限每個整點 \((x, y)\) 的權值為 \(f(y) g(x)\)。想象反比例函數 \(y = \dfrac n x\)，它與 \(x, y\) 軸正半軸圍成的區域內所有整點的權值和為 \(S = \sum\limits_{xy\leq n} f(y)g(x)\)。當 \(x = 1\) 時，\(\sum\limits_{y = 1} ^ n f(y)\) 即 \(s(n)\) 貢獻至 \(S\)。當 \(x > 1\) 時，考慮一個橫座標區間 \([L, R](2\leq L\leq R\leq n)\)。若對於任意 \(x\in [L, R]\) 滿足 \(\left\lfloor\dfrac n x\right\rfloor\) 相等，即 \(\left\lfloor\dfrac n L\right\rfloor = \left\lfloor\dfrac n R\right\rfloor\)，則該橫座標區間所有產生貢獻的點形成矩形 \([L, R] \times \left[1, \left\lfloor\dfrac n L\right\rfloor\right]\)，它們的權值和即 \(\left(\sum\limits_{x = L} ^ R g(x) \right) s\left(\dfrac n L\right)\)。由於整除值數量為 \(\mathcal{O}(\sqrt n)\)，所以 \(S\) 可寫為 \(\mathcal{O}(\sqrt n)\) 個矩形的和。稍作變形即得 \(s(n)\) 的遞推式。

複雜度分析：由遞推式可知求解 \(s(n)\) 的複雜度為 \(n\) 的所有整除值的根號和。考慮 \(> \sqrt n\) 的整除值的貢獻，即 \(\sum\limits_{d = 1} ^ {\sqrt n} \sqrt {\frac n d}\)。\(\int \sqrt{n} x ^ {-\frac 1 2} dx = 2\sqrt n x ^ {\frac 1 2}\)，將 \(x = \sqrt n\) 帶入，得 \(2n ^ {\frac 3 4}\)。而小於 \(\sqrt n\) 的整除值的貢獻為 \(\sum\limits_{d = 1} ^ {\sqrt n} \sqrt d\)。\(\int \sqrt x dx = \frac 2 3 x ^ {\frac 3 2}\)，將 \(x = \sqrt n\) 帶入，得 \(\frac 2 3 n ^ {\frac 3 4}\)。因此總複雜度為 \(\mathcal{O}(n ^ {\frac 3 4})\)。

在複雜度分析過程中我們還得到了一個有趣的結論：大於 \(\sqrt n\) 和小於 \(\sqrt n\) 的整除值的根號和級別相等。對於筆者而言，這個結論出乎意料。

一般預處理 \(f\) 及其字首和到 \(n ^ {\frac 2 3}\) 處，複雜度優化為 \(n ^ {\frac 2 3} + \sqrt n (n ^ {\frac 1 3}) ^ {\frac 1 2} = \mathcal{O}(n ^ {\frac 2 3})\)。

6.2 例題

I. P4213 【模板】杜教篩（Sum）

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr int N = 5e6 + 5;
bool vis[N];
int cnt, pr[N], mu[N], phi[N], smu[N];
ll sphi[N];
unordered_map<int, ll> p, m;
ll dp(int n) {
  if(n < N) return sphi[n];
  auto it = p.find(n);
  if(it != p.end()) return it->second;
  ll sum = 1ll * n * (n + 1ll) / 2;
  for(int l = 2, r; ; l = r + 1) {
    r = n / (n / l);
    sum -= (r - l + 1) * dp(n / l);
    if(r == n) break;
  }
  return p[n] = sum;
}
int dm(int n) {
  if(n < N) return smu[n];
  auto it = m.find(n);
  if(it != m.end()) return it->second;
  ll sum = 1;
  for(int l = 2, r; l <= n; l = r + 1) {
    r = n / (n / l);
    sum -= (r - l + 1) * dm(n / l);
    if(r == n) break;
  }
  return m[n] = sum;
}
int main() {
  mu[1] = phi[1] = 1;
  for(int i = 2; i < N; i++) {
    if(!vis[i]) pr[++cnt] = i, mu[i] = -1, phi[i] = i - 1;
    for(int j = 1; j <= cnt && i * pr[j] < N; j++) {
      vis[i * pr[j]] = 1;
      if(i % pr[j] == 0) {
        phi[i * pr[j]] = phi[i] * pr[j];
        break;
      }
      phi[i * pr[j]] = phi[i] * (pr[j] - 1);
      mu[i * pr[j]] = -mu[i];
    }
  }
  for(int i = 1; i < N; i++) smu[i] = smu[i - 1] + mu[i], sphi[i] = sphi[i - 1] + phi[i];
  int T, n;
  cin >> T;
  while(T--) {
    cin >> n;
    cout << dp(n) << " " << dm(n) << "\n";
  }
  return 0;
}

參考文章

第一章：

• 數論函數 - 百度百科。
• 積性函數 - OI Wiki。
• 狄利克雷折積 - OI Wiki。

第三章：

• 複雜度分析：積性函數的狄利克雷折積 - EntropyIncreaser。

第六章：

• 演演算法學習筆記 52：杜教篩 - Pecco。