首先我們來看看一個範例:
\[\begin{aligned}
&min &f(x,y)&=x^2+y^2\\
&s.t. &xy&=3
\end{aligned}
\]
即:在定義域\(xy=3\)內,求\(f(x,y)\)的最小值。
兩個函數的影象如下:
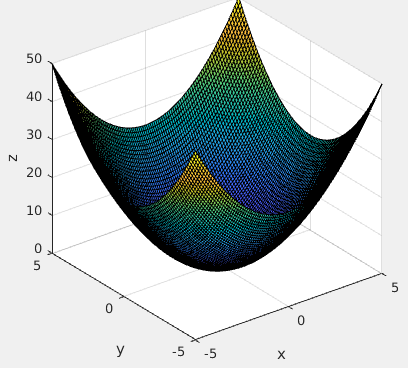
$z=x^2+y^2$
|
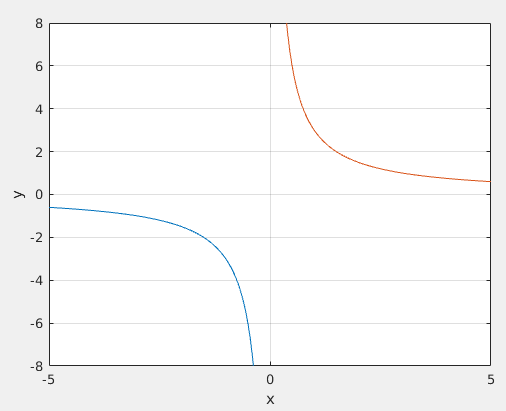
$xy=3$
|
讓我們把兩個影象融合到一起:
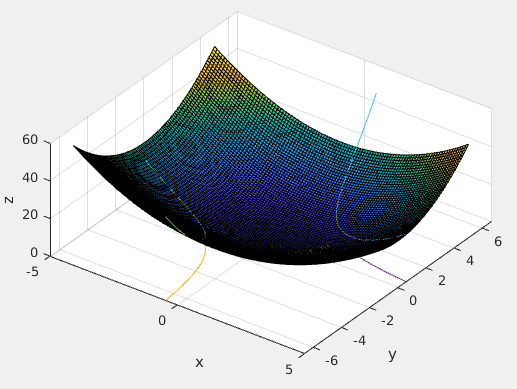
$z=x^2+y^2$與$xy=3$
在\(z=x^2+y^2\)上劃過的兩個拋物線就是當點\((x,y)\)滿足\(xy=3\)時的點在\(z\)上的取值。這兩條拋物線上的點\((x,y,z)\)一 一對應著二維平面上的點\((x,y)\)。二維平面上的兩條雙曲線就是當前問題的可行域(滿足約束條件的點的集合)的視覺化表示。現在讓我們來看看對\(z\)從最底部往上開始做水平切割,每次的切口都是一個圓,每個圓都對應著下面的二維平面上的一個圓,即等高線。隨著往上攀爬,切口的圓表示的\(z\)值越來越大,對應的等高線圓的也越來越大,當切口碰到那兩條拋物線時,也就是在可行域內,\(z\)取到了值,之前的值雖然都比現在的小,但是不作數,因為當時的值對應的點\((x,y)\)不在可行域內。繼續往上,我們知道,\(z\)的取值會變大,也就是說,只有在切口圓第一次碰到拋物線的時候,\(z\)便已經取到了最大值,此時的切口圓對應的二維平面上的圓剛好與雙曲線相切。
現在讓我們回到二維的平面,來看看相切時有什麼等式成立:
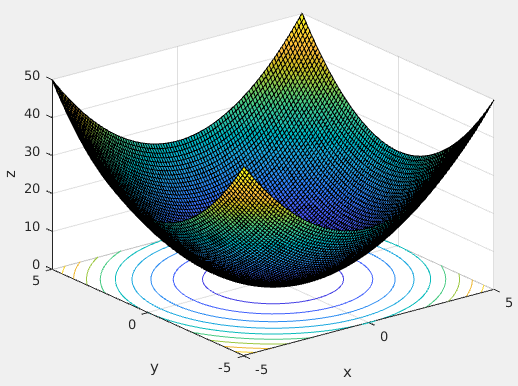
$z=x^2+y^2$及其等高線
|

$xy=3$
|
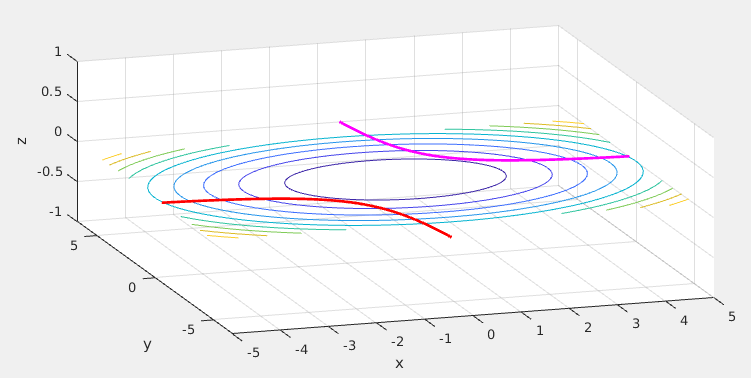
三維視角下相切時可行域曲線與目標函數等高線
|
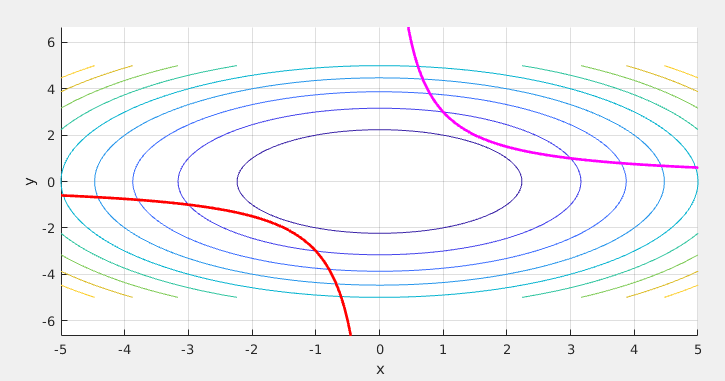
二維視角下相切時可行域曲線與目標函數等高線
|
在相切時取最小值,另外在相切時有以下等式成立(下式為自己的理解,沒有參考書籍,可能有誤):
\[{\nabla}_{x,y} f(x,y) = \lambda \vec{w_g},\lambda \in R
\]
其中,$ \vec{w_g} $ 表示函數\(g\)的法向量,$ {\nabla}_{x,y} f(x,y) $ 為函數\(f(x,y)\)在相切點\((x,y)\)的梯度。
通過上式,我們可以得到:
\[\left(\frac{\Delta f(x,y)}{\Delta x} ,\frac{\Delta f(x,y)}{\Delta y}\right) = \lambda \left(\vec{w_gx},\vec{w_gy} \right)
\]
即:
\[\begin{aligned}
2x &= \lambda y\\
2y &= \lambda x
\end{aligned}
\]
另外,我們有:
\[xy=3
\]
綜合這三個等式,得到:
\[(x,y) \in \{(\sqrt{3},\sqrt{3}),(-\sqrt{3},-\sqrt{3})\}
\]
所以\(min f(x,y) = 6\)。
其實我不是很明白為什麼低維的成立後,就可以運用到高維,而且高維的情況基本上都是重複幾次低維的情況即可。
另外,我們常見的拉格朗日乘數法的形式為:
\[\begin{aligned}
& min &&z=f(x,y) \\
& s.t. &&c_i(x,y)=0, i=1,2,...,n
\end{aligned}
\]
其寫成拉格朗日函數的形式為:
\[min \space L(x,\alpha,\beta) = min (f(x,y) + \sum^{n}_{i=1} \lambda_i c_i(x,y))
\]
其實可以理解為:在可行域內,找到能夠使\(f(x,y)\)的等高線,與所有\(c\),同時相切的,所有\((x,y)\)對應的值。另外, \(\sum^{n}_{i=1} \lambda_i c_i(x,y))\) 可以看作是由多個函陣列成的,單個函數,讓我們記作為\(\psi\)。那麼就可以套用上面的例子裡面的推理過程,即:
\[\left(\frac{\Delta f(x,y)}{\Delta x} ,\frac{\Delta f(x,y)}{\Delta y}\right) =
\lambda \left(\frac{\Delta \psi}{\Delta x} ,\frac{\Delta \psi}{\Delta y} \right) =
\lambda_1 \left(\frac{\Delta c_1(x,y)}{\Delta x} ,\frac{\Delta c_1(x,y)}{\Delta y} \right) +
\lambda_2 \left(\frac{\Delta c_2(x,y)}{\Delta x} ,\frac{\Delta c_2(x,y)}{\Delta y} \right) +
\cdots+
\lambda_n \left(\frac{\Delta c_n(x,y)}{\Delta x} ,\frac{\Delta c_n(x,y)}{\Delta y} \right)
\]
即(注意,下面的\(\lambda_i\)與上面的\(\lambda_i\)不是同一個):
\[\begin{aligned}
\frac{\Delta f(x,y)}{\Delta x} &= \lambda_1 \frac{\Delta c_1(x,y)}{\Delta x}\\
\frac{\Delta f(x,y)}{\Delta y} &= \lambda_1 \frac{\Delta c_1(x,y)}{\Delta y}\\
\frac{\Delta f(x,y)}{\Delta x} &= \lambda_2 \frac{\Delta c_2(x,y)}{\Delta x}\\
\frac{\Delta f(x,y)}{\Delta y} &= \lambda_2 \frac{\Delta c_2(x,y)}{\Delta y}\\
& \space \space \vdots \\
\frac{\Delta f(x,y)}{\Delta x} &= \lambda_n \frac{\Delta c_n(x,y)}{\Delta x}\\
\frac{\Delta f(x,y)}{\Delta y} &= \lambda_n \frac{\Delta c_n(x,y)}{\Delta y}\\
\end{aligned}
\]
對於每組待解變數\((x,y,\lambda_i)\),都有三個方程組:
\[\begin{aligned}
&f(x,y)=0, \\
&\frac{\Delta f(x,y)}{\Delta x} = \lambda_n \frac{\Delta c_n(x,y)}{\Delta x},\\
&\frac{\Delta f(x,y)}{\Delta y} = \lambda_n \frac{\Delta c_n(x,y)}{\Delta y}\\
\end{aligned}
\]
所以,是能夠解出\((x,y)\)的。
參考文獻:
拉格朗日乘數法 —— 通俗理解






