1. 陣列的旋轉總結

陣列的旋轉指的是將陣列的最後若干個數提前到陣列前面，陣列的翻轉指的是將陣列的順序顛倒。旋轉可以通過多次翻轉實現。

陣列的翻轉很簡單，通過雙指標來實現：交換陣列的第一個數和最後一個數，交換第二個數和倒數第二個數，一直到陣列中間即可。

2. 題目記錄

189. 輪轉陣列

分析題意

給你一個陣列，將陣列中的元素向右輪轉 k **個位置，其中 k **是非負數。

思路分析

其實題目就是一個陣列旋轉問題，我們可以通過圖片來分析一下：

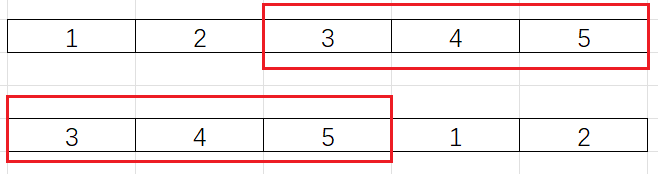
將上面這個陣列向右輪轉3個位置，其實就是：將陣列的後3個元素旋轉到陣列前面，即：陣列的旋轉。前面我們講到：陣列的旋轉可以通過多次陣列翻轉來實現：

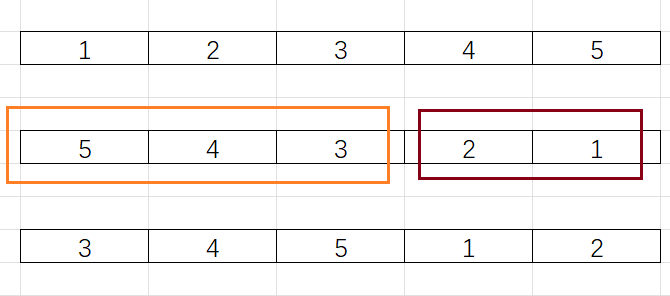
我們首先對整個陣列進行翻轉，然後對每一個子陣列進行翻轉，即：陣列的旋轉通過三次陣列的翻轉來實現。

class Solution {
    public void rotate(int[] nums, int k) {
        k = k % nums.length;
        // 整個陣列進行翻轉
        reverse(nums, 0, nums.length - 1);
        // 前k個元素進行翻轉
        reverse(nums, 0, k - 1);
        // 剩餘元素進行翻轉
        reverse(nums, k, nums.length - 1);

    }

    void reverse(int[] nums, int left, int right){
        int temp = 0;
        while(left < right){
            temp = nums[left];
            nums[left] = nums[right];
            nums[right] = temp;
            left ++;
            right --;
        }
    }
}

複雜度分析

時間複雜度：\(O(n)\)
空間複雜度：\(O(1)\)

396. 旋轉函數

分析題意

看到題目似乎我們需要模擬旋轉操作，然後求出每次旋轉之後的總和，並所有旋轉總和中取最大值。

但其實只求最大值的話，我們無需進行模擬。讓我們來看看不同旋轉操作之間的規律性：

a = (0 * 4) + (1 * 3) + (2 * 2) + (3 * 6)
b = (1 * 4) + (2 * 3) + (3 * 2) + (0 * 6)
c = (2 * 4) + (3 * 3) + (0 * 2) + (1 * 6)
d = (3 * 4) + (0 * 3) + (1 * 2) + (2 * 6)

從上面我們可以分析一下a、b、c和d之間的關係：

b = a + 4 + 3 + 2 + 6 - 4 * 6
c = b + 4 + 3 + 2 + 6 - 4 * 2
d = c + 4 + 3 + 2 + 1 - 4 * 3

每次都等於上次的和加上陣列總和減去當前遍歷到的元素的n倍。

思路分析

class Solution {
    public int maxRotateFunction(int[] nums) {
        int sum = 0;
        int ans = 0;
        for(int i = 0; i < nums.length; i++){
            ans = ans + i * nums[i];
            sum += nums[i];
        }

        int pre = ans;
        for(int i = nums.length - 1; i >= 0; i--){
            pre = pre + sum - nums.length * nums[i];
            ans = Math.max(ans, pre);
        }
        return ans;
    }
}

複雜度分析

時間複雜度：\(O(n)\)

空間複雜度：\(O(1)\)