列印陣列的所有子集

作者：Grey

原文地址：

無重複值情況

主要思路

定義遞迴函數

void p(int[] arr, int i, LinkedList<Integer> pre, List<List<Integer>> result)

遞迴含義是：陣列arr從i往後開始收集所有的子集，i之前生成的子集是pre，所有生成的子集都存在result中，

base case 就是，當i來到arr.length位置的時候，此時，已經沒有選的字元了，將收集到的pre加入result中，

針對普遍情況，可能性有兩種，第一種，不要選擇i位置的元素，那麼接下來直接呼叫p(arr, i + 1, pre, result)

第二種情況，選擇i位置的元素，則將i位置的元素加入pre的下一個位置中，即:pre.addLast(arr[i])，然後去下一個位置做決策，即p(arr, i + 1, pre, result)。

第二種情況中，不要忘記選擇了i位置的元素，在後續決策完畢後，需要恢復現場，即pre.removeLast()。

完整程式碼見

class Solution {
    public static List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        p(nums, 0, new LinkedList<>(), result);
        return result;
    }

    // i往後收集所有的子集
    public static void p(int[] arr, int i, LinkedList<Integer> pre, List<List<Integer>> result) {
        if (i == arr.length) {
            List<Integer> ans = new ArrayList<>(pre);
            result.add(ans);
        } else {
            // 不要i位置
            p(arr, i + 1, pre, result);
            pre.addLast(arr[i]);
            // 要i位置
            p(arr, i + 1, pre, result);
            // 恢復現場
            pre.removeLast();
        }
    }
}

有重複值情況

題目描述見: LeetCode 90. Subsets II

上一個問題由於題目限定了，沒有重複元素，所以處理相對簡單一些，本題說明了輸入引數中可能會有重複的元素，且生成的子集不能有重複，此時有兩個思路：

第一個思路，基於上一個問題的結果，即result，做去重操作，思路比較簡單，但是複雜度會相對高一些，因為我們每次都要全量得到所有的子集，然後最後才去重。

第二個思路，在執行遞迴函數的時候，可以做一些剪枝，無須到最後再來去重，直接在遞迴函數中就把結果生成出來。接下來講第二個解法的思路。

由於題目中已經說明，返回子集的順序無要求，那麼，我們可以首先將陣列進行排序，排序後，所有相同的元素一定會排列到一起，然後定義一個和上一題一樣的遞迴函數

void p(int[] nums, int i, LinkedList<Integer> pre, List<List<Integer>> result)

遞迴含義是：陣列arr從i往後開始收集所有的無重複子集，i之前生成的子集是pre，所有生成的子集都存在result中。

接下來分析遞迴函數的可能性，我們可以不要選擇i位置的元素，那麼則可以直接加入result.add(new ArrayList<>(pre))，按上一題邏輯，接下來我們應該去i+1位置收集結果，但是，由於有重複元素，所以接下來i，i+1,……i + n 都有可能是同一個元素，範例圖如下

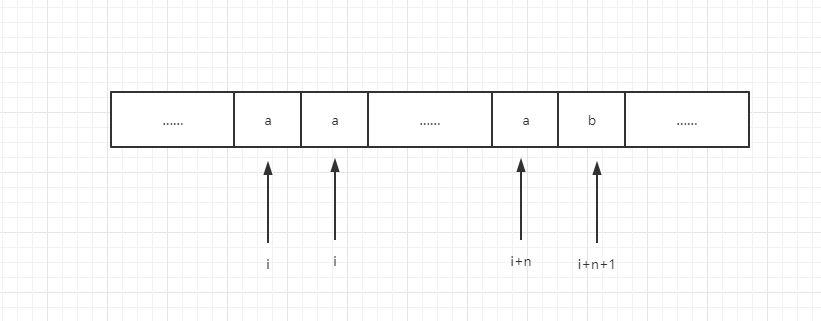
如上圖，i一直到i+n都是元素a,直到i+n+1才是一個不同的元素，所以，當我們收集了i位置的元素以後，我們不能直接去i+1位置收集，而是應該從i+n+1位置開始收集。

完整程式碼見

class Solution {
    public static List<List<Integer>> subsetsWithDup(int[] nums) {
        List<List<Integer>> lists = new ArrayList<>();
        Arrays.sort(nums);
        p(nums, 0, new LinkedList<>(), lists);
        return lists;
    }

    public static void p(int[] nums, int i, LinkedList<Integer> pre, List<List<Integer>> result) {
        result.add(new ArrayList<>(pre));
        for (int s = i; s < nums.length; s++) {
            // 一直到下一個不等於s位置元素的地方
            if (s > i && nums[s] == nums[s - 1]) {
                continue;
            }
            pre.add(nums[s]);
            p(nums, s + 1, pre, result);
            pre.remove(pre.size() - 1);
        }
    }
}

演演算法和資料結構筆記

列印陣列的所有子集

列印陣列的所有子集

無重複值情況

有重複值情況

更多