單調棧的本質與應用
單調棧的定義與證明
前言
最近領悟到了單調棧的本質,特此來記錄一下我的理解。
單調棧主要用來解決這樣一類問題,當列舉到下標$i$,要求在下標$i$之前小於$/$大於$val$的數的下標中,找到最小$/$最大的下標位置。
一共有四種不同的情況,下面來證明在這四種情況中,棧內維護的元素始終單調遞增或單調遞減的。
在小於$val$的數中找到最小下標
當我們列舉到下標$i$,同時給定一個數$val$,現在我們要在下標$i$之前的數中找到滿足數值小於$val$的數的下標,然後在這些滿足條件的數的下標中找到最小的下標。
很容易想到的一個做法是從前面開始暴力列舉每一個數,如果找到第一個小於$val$的數,那麼就返回這個數的下標,這個下標一定是最小的下標。一共有$n$次詢問,而每次詢問都要用$O(n)$的計算量去找到最小的下標,因此暴力做法的時間複雜度是$O(n^2)$,這個時間複雜度就太高了,我們需要對它進行優化。
我們用一個棧去模擬上面暴力列舉的過程。一開始棧為空,每當$i$往右走,就往棧壓入一個元素(這裡壓入的是下標),因此當列舉到$i$時,棧裡儲存的是下標$1 \sim i-1$(下標從$1$開始),每次要找最小下標時都是從棧底開始找(即棧裡存下標$1$的位置開始找),直到找到第一個比$val$小的下標所對應的數為止。既然可以對這個過程進行優化,那麼意味著存在冗餘,我們看一下棧裡是否存在某些元素永遠也不會作為答案輸出來。
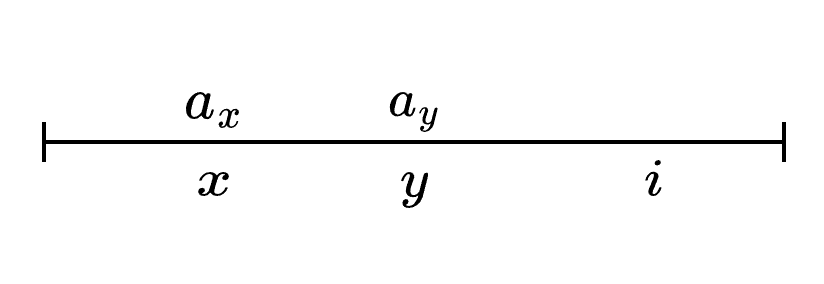
假設有位置$x < y$,同時下標所對應的數$a_x \leq a_y$,那麼$a_y$就沒有存在的必要了。這是因為如果$a_y < val$,那麼就一定有$a_x < val$,而$a_x$所對應的下標小於$a_y$所對應的下標,即$x < y$,因此肯定要選$x$而不是$y$。
因此結論就是如果前一個數要比後一個數小(相等)的話,那麼後一個數就沒有存在的必要了。
因此對於某個位置$j~(j < i)$,把$j+1 \sim i-1$這些位置上大於$a_j$的下標刪去,最後整個棧的元素就是單調遞減的,如圖:
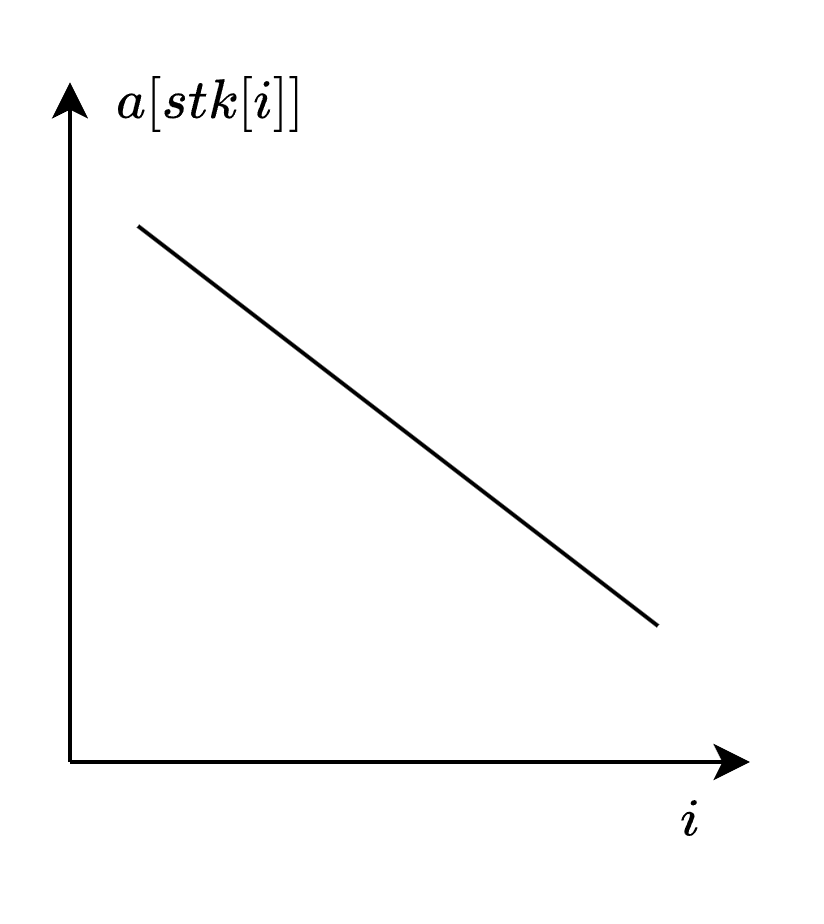
現在我們要在這個序列中找到小於$val$的最小的下標,由於滿足單調性就可以用二分來做。
然後現在要把下標$i$壓入棧中,由於此時剛遍歷完$i$,在棧中$i$後面沒有數,因此不用考慮後面是否有比這個$i$位置上大的數。而要考慮$i$前面的下標,只有當$a_i$小於棧頂元素所對應的數$a[stk[tp]]$時,才能將下標$i$壓入棧,這是因為前面的數要比後面的數小,否則後面的數要被刪除。如果每次都根據這個規則來將元素壓入棧這樣就能保證棧中元素是單調遞減的了。
在小於$val$的數中找到最大下標
當我們列舉到下標$i$,同時給定一個數$val$,現在我們要在下標$i$之前的數中找到滿足數值小於$val$的數的下標,然後在這些滿足條件的數的下標中找到最大的下標。
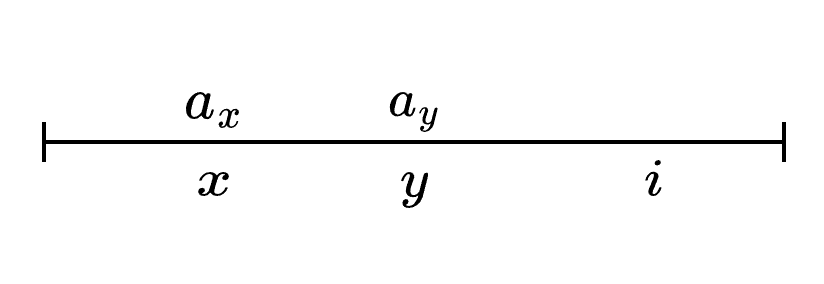
假設有位置$x < y$,同時下標所對應的數$a_x \geq a_y$,那麼$a_x$就沒有存在的必要了。這是因為如果$a_x < val$,那麼就一定有$a_y < val$,而$a_y$所對應的下標大於$a_x$所對應的下標,即$y > x$,因此肯定要選$y$而不是$x$。
因此結論就是如果前一個數要比後一個數大(相等)的話,那麼前一個數就沒有存在的必要了。
因此對於某個位置$j~(j < i)$,把下標$j$之前的位置上大於$a_j$的下標刪去,最後整個棧的元素就是單調遞增的,如圖:
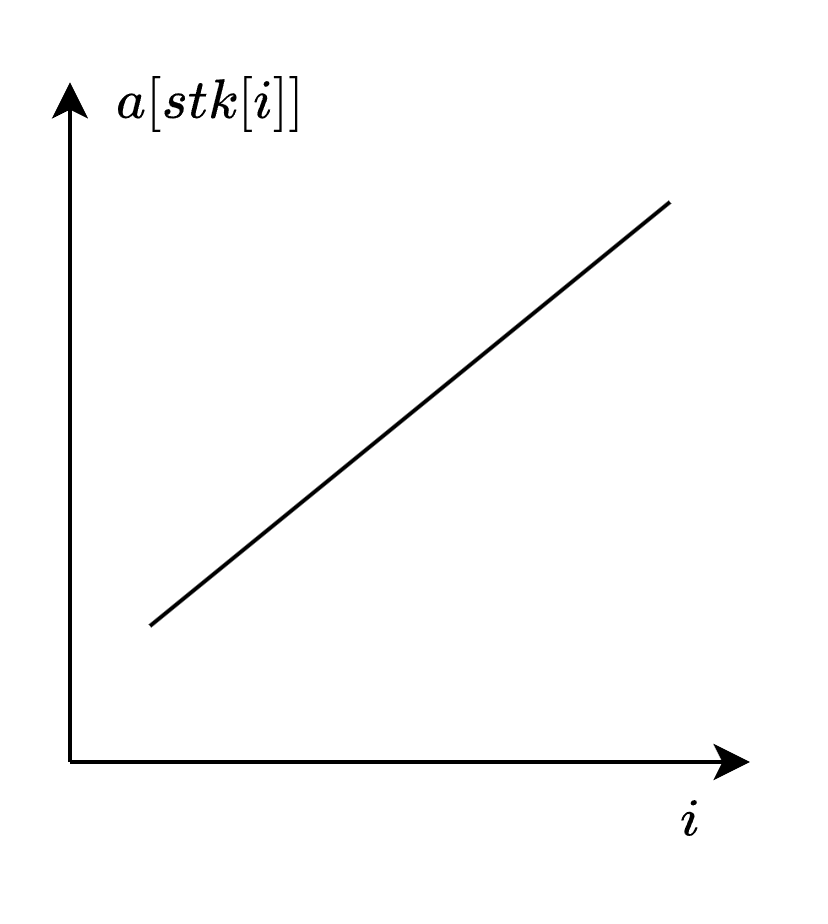
現在我們一樣用上面的方法,即通過二分來找到這個序列中小於$val$的最大的下標,這樣做肯定是正確的。
然後現在要把下標$i$壓入棧中,此時$i$後面沒有數且這種情況只考慮前面位置的數,那麼我們只需要看棧中存放的下標就可以了。由於棧中存放的下標都是小於$i$的,並且根據前面結論如果前一個數要比後一個數大(相等)的話,那麼就把前一個數刪掉,因此我們每次彈出棧頂元素,比較$a[stk[tp]]$與$a[i]$的大小,如果發現$a[stk[tp]] \geq a[i]$,那麼那麼就應該把棧頂元素刪除,重複這個過程直到棧為空(意味著前面所有元素都比$a[i]$大或相等)或者有$a[stk[tp]] < a[i]$(前面剩下的元素都是小於$a[i]$的)。這樣將元素壓入棧就能保證棧中元素是單調遞增的了。
可以發現,上面將$i$壓入棧的過程就已經找到了比$a[i]$小的數的最大下標了,因此就沒必要再用二分了。
在大於$val$的數中找到最小下標
當我們列舉到下標$i$,同時給定一個數$val$,現在我們要在第$i$個下標之前的數中找到滿足數值大於$val$的數的下標,然後在這些滿足條件的數的下標中找到最小的下標。
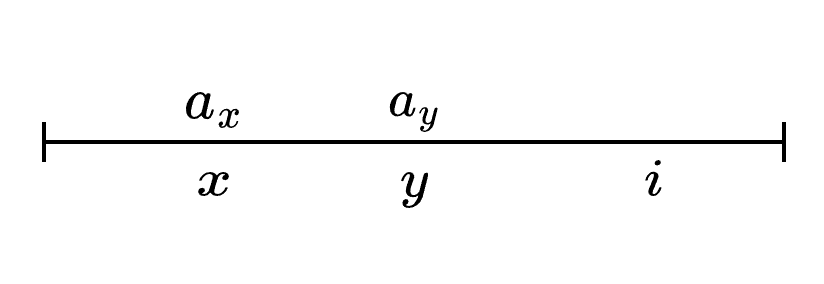
假設有位置$x < y$,同時下標位置上的數$a_x \geq a_y$,那麼$a_y$就沒有存在的必要了。這是因為如果$a_y > val$,那麼就一定有$a_x > val$,而$a_x$所對應的下標小於$a_y$所對應的下標,即$x < y$,因此肯定要選$x$而不是$y$。
因此結論就是如果前一個數要比後一個數大(相等)的話,那麼後一個數就沒有存在的必要了。
因此對於某個位置$j~(j < i)$,把$j+1 \sim i-1$這些位置上小於$a_j$的下標刪去,最後整個棧的元素就是單調遞增的,如圖:

現在我們要在這個序列中找到大於$val$的最小的下標,由於滿足單調性就可以用二分來做。
然後現在要把下標$i$壓入棧中,由於此時剛遍歷完$i$,棧中的$i$後面沒有數,因此不用考慮後面是否有比這個$i$位置上小的數。而要考慮$i$前面的下標,只有當$a_i$大於棧頂元素所對應的數$a[stk[tp]]$時,才能將下標$i$壓入棧,這是因為前面的數要比後面的數小,否則後面的數要被刪除。如果每次都根據這個規則來將元素壓入棧這樣就能保證棧中元素是單調遞增的了。
在大於$val$的數中找到最大下標
當我們列舉到下標$i$,同時給定一個數$val$,現在我們要在第$i$個下標之前的數中找到滿足數值大於$val$的數的下標,然後在這些滿足條件的數的下標中找到最大的下標。
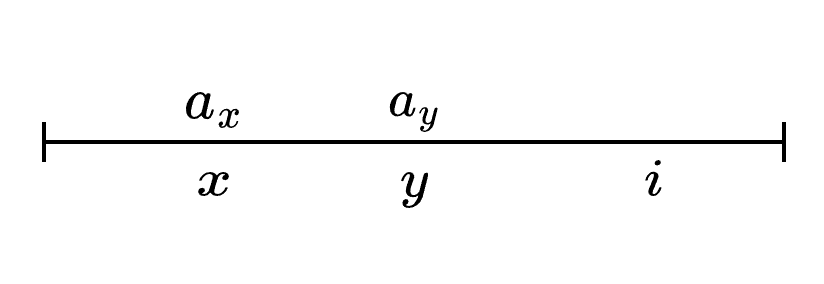
假設有位置$x < y$,同時下標位置上的數$a_x \leq a_y$,那麼$a_x$就沒有存在的必要了。這是因為如果$a_x > val$,那麼就一定有$a_y > val$,而$a_y$所對應的下標大於$a_x$所對應的下標,即$y > x$,因此肯定要選$y$而不是$x$。
因此結論就是如果前一個數要比後一個數小(相等)的話,那麼前一個數就沒有存在的必要了。
因此對於某個位置$j~(j < i)$,把下標$j$之前的位置上小於$a_j$的下標刪去,最後整個棧的元素就是單調遞減的,如圖:

先考慮把下標$i$壓入棧,此時$i$後面沒有數且這種情況只考慮前面的數,那麼我們只需要看棧中存放的下標就可以了。由於棧中存放的下標都是小於$i$的,並且根據前面結論如果前一個數要比後一個數小(相等)的話,那麼就把前一個數刪掉,因此我們每次彈出棧頂元素,比較$a[stk[tp]]$與$a[i]$的大小,如果發現$a[stk[tp]] \leq a[i]$,那麼那麼就應該把棧頂元素刪除,重複這個過程直到棧為空(意味著前面所有元素都比$a[i]$小或相等)或者有$a[stk[tp]] > a[i]$(前面剩下的元素都是大於$a[i]$的)。這樣將元素壓入棧就能保證棧中元素是單調遞增的了,同時這個過程也找到棧中比$a[i]$大的數的最大下標,不需要二分。
總結
- 要在小於$val$的數中找到最小下標,這種情況的棧是單調遞減的,找到最小下標需要用到二分,只有當前下標所對應的數小於棧頂元素所對應的數時才可以壓入棧。
- 要在小於$val$的數中找到最大下標,這種情況的棧是單調遞增的,找到最大下標不需要用到二分,持續彈出棧頂元素直到棧頂元素所對應的數小於當前下標所對應的數,此時棧頂元素就是最大下標,同時把當前下標壓入棧。
- 要在大於$val$的數中找到最小下標,這種情況的棧是單調遞增的,找到最小下標需要用到二分,只有當前下標所對應的數大於棧頂元素所對應的數時才可以壓入棧。
- 要在大於$val$的數中找到最大下標,這種情況的棧是單調遞減的,找到最大下標不需要用到二分,持續彈出棧頂元素直到棧頂元素所對應的數大於當前下標所對應的數,此時棧頂元素就是最大下標,同時把當前下標壓入棧。
現在來看的話理解單調棧這個模型並沒有太大的困難,關鍵是在做題的時候要抽象出這個模型,這樣才可以用上面的方法來解題。
下面來舉例幾個用到單調棧的題目,都需要將這個模型抽象出來。
單調棧
給定一個長度為 $N$ 的整數數列,輸出每個數左邊第一個比它小的數,如果不存在則輸出 $−1$。
輸入格式
第一行包含整數 $N$,表示數列長度。
第二行包含 $N$ 個整數,表示整數數列。
輸出格式
共一行,包含 $N$ 個整數,其中第 $i$ 個數表示第 $i$ 個數的左邊第一個比它小的數,如果不存在則輸出 $−1$。
資料範圍
$1 \leq N \leq {10}^{5}$
$1 \leq \text{數列中元素} \leq {10}^{9}$
輸入樣例:
5 3 4 2 7 5
輸出樣例:
-1 3 -1 2 2
解題思路
題目要求對於每個位置上的數找到左邊第一個比它小的數,也就是說對於下標$i$位置上的數$a_i$,要在下標$i$之前找到所有小於$a_i$的數中下標最大的那個。這個就是我們上面說到的在小於$val$的數中找到最大下標這個模型。現在已經把模型抽象出來了,下面就可以用程式碼實現了。
AC程式碼如下,時間複雜度為$O(n)$:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 const int N = 1e5 + 10; 5 6 int a[N]; 7 int stk[N], tp; 8 9 int main() { 10 int n; 11 scanf("%d", &n); 12 for (int i = 1; i <= n; i++) { 13 scanf("%d", a + i); 14 } 15 16 for (int i = 1; i <= n; i++) { 17 while (tp && a[stk[tp]] >= a[i]) { // 把>=a[i]的棧頂元素全部彈出 18 tp--; 19 } 20 if (tp) printf("%d ", a[stk[tp]]); // 此時棧頂元素就是最大下標 21 else printf("-1 "); // 棧為空表示i前面不存在小於a[i]的數 22 stk[++tp] = i; // 此時棧頂元素必然小於a[i],把i壓入棧中 23 } 24 25 return 0; 26 }
以下內容是線段樹以及樹狀陣列的解法,可以略過。
順便擴充套件一下,這題還可以用線段樹來做。用到的是值域線段樹,即線段樹維護的是值域$a_i$的若干個區間,而不是下標區間。每次詢問都是要找小於$a_i$的最大下標,因此可以用線段樹來維護每個數值所對應的最大下標,即每次查詢都問某個字首區間的最大值。由於數值的取值範圍很大,因此需要進行離散化。
AC程式碼如下,時間複雜度為$O(n \log{n})$:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 const int N = 1e5 + 10; 5 6 int a[N]; 7 int xs[N], sz; 8 struct Node { 9 int l, r, maxv; 10 }tr[N * 4]; 11 12 void build(int u, int l, int r) { 13 if (l == r) { 14 tr[u] = {l, r}; 15 } 16 else { 17 int mid = l + r >> 1; 18 build(u << 1, l, mid); 19 build(u << 1 | 1, mid + 1, r); 20 tr[u] = {l, r}; 21 } 22 } 23 24 void modify(int u, int x, int c) { 25 if (tr[u].l == x && tr[u].r == x) { 26 tr[u].maxv = max(tr[u].maxv, c); 27 } 28 else { 29 if (x <= tr[u].l + tr[u].r >> 1) modify(u << 1, x, c); 30 else modify(u << 1 | 1, x, c); 31 tr[u].maxv = max(tr[u << 1].maxv, tr[u << 1 | 1].maxv); 32 } 33 } 34 35 int query(int u, int l, int r) { 36 if (tr[u].l >= l && tr[u].r <= r) return tr[u].maxv; 37 int mid = tr[u].l + tr[u].r >> 1, ret = 0; 38 if (l <= mid) ret = query(u << 1, l, r); 39 if (r >= mid + 1) ret = max(ret, query(u << 1 | 1, l, r)); 40 return ret; 41 } 42 43 int find(int x) { 44 int l = 1, r = sz; 45 while (l < r) { 46 int mid = l + r >> 1; 47 if (xs[mid] >= x) r = mid; 48 else l = mid + 1; 49 } 50 return l; 51 } 52 53 int main() { 54 int n; 55 scanf("%d", &n); 56 for (int i = 1; i <= n; i++) { 57 scanf("%d", a + i); 58 xs[++sz] = a[i]; 59 } 60 61 sort(xs + 1, xs + sz + 1); 62 sz = unique(xs + 1, xs + sz + 1) - xs - 1; 63 64 build(1, 1, sz); 65 66 for (int i = 1; i <= n; i++) { 67 int t = query(1, 1, find(a[i]) - 1); // 如果是qurty(1, 1, 0)那麼會返回0 68 modify(1, find(a[i]), i); 69 printf("%d ", t ? a[t] : -1); 70 } 71 72 return 0; 73 }
這裡有個小技巧,就是由於詢問的是$< a_{i}$的數,即詢問$\leq a_{i}-1$的數,由於我們會用到$a_{i}-1$,因此應該把$a_{i}-1$也進行離散化的,但可以發現上面的程式碼並沒有這麼做。其實可以發現本質上是找$a_{i}$的前一個數,即便我們把$a_{i}-1$進行離散化,也不會對$a_{i}-1$進行任何修改操作,於是可以不對$a_{i}-1$進行離散化,而直接把$a_{i}$離散化後的前一個位置作為前一個數。這種做法可以降低一下常數,防止被卡。
可以發現由於每次詢問的區間都是以開始$1$開始的字首的最大值,因此這裡還可以用樹狀陣列來實現,AC程式碼如下,時間複雜度為$O(n \log{n})$:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 const int N = 1e5 + 10; 5 6 int a[N]; 7 int xs[N], sz; 8 int tr[N]; 9 10 int lowbit(int x) { 11 return x & -x; 12 } 13 14 void add(int x, int c) { 15 for (int i = x; i <= sz; i += lowbit(i)) { 16 tr[i] = max(tr[i], c); 17 } 18 } 19 20 int query(int x) { 21 int ret = 0; 22 for (int i = x; i; i -= lowbit(i)) { 23 ret = max(ret, tr[i]); 24 } 25 return ret; 26 } 27 28 int find(int x) { 29 int l = 1, r = sz; 30 while (l < r) { 31 int mid = l + r >> 1; 32 if (xs[mid] >= x) r = mid; 33 else l = mid + 1; 34 } 35 return l; 36 } 37 38 int main() { 39 int n; 40 scanf("%d", &n); 41 for (int i = 1; i <= n; i++) { 42 scanf("%d", a + i); 43 xs[++sz] = a[i]; 44 } 45 46 sort(xs + 1, xs + sz + 1); 47 sz = unique(xs + 1, xs + sz + 1) - xs - 1; 48 49 for (int i = 1; i <= n; i++) { 50 int t = query(find(a[i]) - 1); // 如果是query(0)那麼會返回0 51 printf("%d ", t ? a[t] : -1); 52 add(find(a[i]), i); 53 } 54 55 return 0; 56 }
其實上面說到的$4$個模式都是可以用線段樹和樹狀陣列實現的,但還是不建議這麼做,一方面是程式碼很難寫,另一方面是常數比較大,同樣是$O(n \log{n})$的複雜度,單調棧的做法就不會被卡,而線段樹或樹狀陣列就很容易被卡常數。
最長連續子序列
給定一個長度為 $n$ 的整數序列 $a_1,a_2, \dots ,a_n$。
現在,請你找到一個序列 $a$ 的連續子序列 $a_{l},a_{l+1}, \dots ,a_{r}$,要求:
- ${\sum\limits_{i=l}^{r}{a_i}} > 100 \times (r - l + 1)$。
- 連續子序列的長度(即 $r−l+1$)儘可能大。
請你輸出滿足條件的連續子序列的最大可能長度。
輸入格式
第一行包含整數 $n$。
第二行包含 $n$ 個整數 $a_1,a_2, \dots ,a_n$。
輸出格式
一個整數,表示最大可能長度。
如果滿足條件的連續子序列不存在,則輸出 $0$。
資料範圍
前三個測試點滿足 $1 \leq n \leq 5$。
所有測試點滿足 $1 \leq n \leq {10}^{6}$,$0 \leq a_i \leq 5000$。
輸入樣例1:
1 5 2 100 200 1 1 1
輸出樣例1:
3
輸入樣例2:
5 1 2 3 4 5
輸出樣例2:
0
輸入樣例3:
2 101 99
輸出樣例3:
1
解題思路
我們把式子做一下等價變換,得到$$\frac{\sum\limits_{i=l}^{r}{a_i}}{r - l + 1} > 100$$可以發現就是區間$l \sim r$的平均數要滿足大於$100$,等價於我們對這個區間的每一個數都減去$100$,最後算得的平均數要大於$0$,證明如下,$$\begin{align*} \frac{\sum\limits_{i=l}^{r}{a_i}}{r - l + 1} &> 100 \\ \frac{\sum\limits_{i=l}^{r}{a_i}}{r - l + 1} - 100 &> 0 \\ \frac{\sum\limits_{i=l}^{r}{a_i - {100 \times (r - l + 1)}}}{r - l + 1} &> 0 \\ \frac{\sum\limits_{i=l}^{r}{(a_i - 100)}}{r - l + 1} &> 0 \end{align*}$$
我們定義$b_i = a_i - 100$,同時用字首和的思想,定義$s_i = \sum\limits_{j=1}^{i}{b_j}$,再把式子進行變換,得到$$\frac{s_{r} - s_{l-1}}{r - l + 1} > 0$$
現在我們要求滿足上式的條件的一個長度最大的區間$l \sim r$,由於$r-l+1 > 0$ 因此可以直接約去分母,上式就變成$s_{r} - s_{l-1} > 0$,即$s_{l'} < s_{r}$(定義${l'} = l-1$,$0 \leq {l'} \leq r-1$),問題就變成了當我們固定了右端點$r$後,要在$r$的左邊找到一個滿足$s_{l'} < s_{r}$,同時為最小的$l'$。
這個就是我們上面說到的在小於$val$的數中找到最小下標這個模型。
AC程式碼如下,時間複雜度為$O(n \log{n})$:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 typedef long long LL; 5 6 const int N = 1e6 + 10; 7 8 LL s[N]; 9 int stk[N], tp; 10 11 int main() { 12 int n; 13 scanf("%d", &n); 14 for (int i = 1; i <= n; i++) { 15 scanf("%d", s + i); 16 s[i] += s[i - 1] - 100; // 求b[i]的字首和,b[i] = a[i] - 100 17 } 18 19 int ret = 0; 20 for (int i = 1; i <= n; i++) { 21 // 當列舉到i,要把前一個元素即i-1壓入棧 22 // 只有棧為空(初始狀態)或s[i-1]小於棧頂元素所對應的數s[stk[tp]]時才能壓入棧 23 if (!tp || s[i - 1] < s[stk[tp]]) stk[++tp] = i - 1; 24 25 // 二分,由於棧內元素式單調遞減的,因此要在下標[0, i-1]中找到小於s[i]最左邊的那個數,對應的是最小下標 26 int l = 1, r = tp; 27 while (l < r) { 28 int mid = l + r >> 1; 29 if (s[stk[mid]] < s[i]) r = mid; 30 else l = mid + 1; 31 } 32 33 if (s[stk[l]] < s[i]) ret = max(ret, i - stk[l]); // 找到才可以作為一個合法的答案 34 } 35 36 printf("%d", ret); 37 38 return 0; 39 }
同時給出樹狀陣列實現的程式碼,由於這題卡常數,因此線段樹的程式碼會TLE,樹狀陣列的時間開銷也比較極限。
AC程式碼如下,時間複雜度為$O(n \log{n})$:

#include <bits/stdc++.h> using namespace std; typedef long long LL; const int N = 1e6 + 10; LL s[N]; LL xs[N], sz; int tr[N]; int find(LL x) { int l = 1, r = sz; while (l < r) { int mid = l + r >> 1; if (xs[mid] >= x) r = mid; else l = mid + 1; } return l; } int lowbit(int x) { return x & -x; } void add(int x, int c) { for (int i = x; i <= sz; i += lowbit(i)) { tr[i] = min(tr[i], c); } } int query(int x) { int ret = N; for (int i = x; i; i -= lowbit(i)) { ret = min(ret, tr[i]); } return ret; } int main() { int n; scanf("%d", &n); for (int i = 1; i <= n; i++) { scanf("%d", s + i); s[i] += s[i - 1] - 100; xs[++sz] = s[i]; } xs[++sz] = 0; sort(xs + 1, xs + sz + 1); sz = unique(xs + 1, xs + sz + 1) - xs - 1; memset(tr, 0x3f, sizeof(tr)); int ret = 0; for (int i = 1; i <= n; i++) { add(find(s[i - 1]), i - 1); ret = max(ret, i - query(find(s[i]) - 1)); } printf("%d", ret); return 0; }
補充我當時想到的思路,當時沒想到平均數這些東西,直接對式子做等價變換,得到$s_{l-1} - 100 \cdot (l + 1) < s_{r} - 100 \cdot r$,這裡的$s_i$是對$a_i$的字首和。然後定義$f(i) = s_{i} - 100 \cdot i$,於是式子就變成了$f(l-1)<f(r)$,即固定了$r$後,要在前面找到滿足小於$f(r)$的最小的$l-1$,然後就想到值域線段樹,不過是用樹狀陣列去實現。
AC程式碼如下,時間複雜度為$O(n \log{n})$:

#include <bits/stdc++.h> using namespace std; typedef long long LL; const int N = 1e6 + 10; LL s[N]; LL xs[N], sz; int tr[N]; LL f(int x) { return s[x] - 100 * x; } int find(LL x) { int l = 1, r = sz; while (l < r) { int mid = l + r >> 1; if (xs[mid] >= x) r = mid; else l = mid + 1; } return l; } int lowbit(int x) { return x & -x; } void add(int x, int c) { for (int i = x; i <= sz; i += lowbit(i)) { tr[i] = min(tr[i], c); } } int query(int x) { int ret = N; for (int i = x; i; i -= lowbit(i)) { ret = min(ret, tr[i]); } return ret; } int main() { int n; scanf("%d", &n); for (int i = 1; i <= n; i++) { scanf("%d", s + i); s[i] += s[i - 1]; xs[++sz] = f(i); } xs[++sz] = 0; sort(xs + 1, xs + sz + 1); sz = unique(xs + 1, xs + sz + 1) - xs - 1; memset(tr, 0x3f, sizeof(tr)); int ret = 0; for (int i = 1; i <= n; i++) { add(find(f(i - 1)), i - 1); ret = max(ret, i - query(find(f(i)) - 1)); } printf("%d", ret); return 0; }
銷售出色區間
給你一份銷售數量表 sales ,上面記錄著某一位銷售員每天成功推銷的產品數目。
我們認為當銷售員同一天推銷的產品數目大於 $8$ 個的時候,那麼這一天就是「成功銷售的一天」。
所謂「銷售出色區間」,意味在這段時間內,「成功銷售的天數」是嚴格 大於「未成功銷售的天數」。
請你返回「銷售出色區間」的最大長度。
範例 1:
輸入:sales = [10,2,1,4,3,9,6,9,9] 輸出:5 解釋:最大銷售出色區間是 [3,9,6,9,9]。
範例 2:
輸入:sales = [5,6,7] 輸出:0
提示:
$1 \leq sales.length \leq {10}^{4}$
$0 \leq sales[i] \leq 16$
解題思路
求一個連續區間的某個數目,應該想到試一下能不能用字首和。先掃描一遍$sales$陣列,同時定義一個陣列$s$,如果$sales[i] > 8$,就把$s[i]$置為$1$,否則就置為$-1$,再對$s$陣列求字首和,那麼問題就變成了我們要在$s$陣列中找到一個最長的區間$[l,r]$,滿足$s_{r} - s_{l-1} > 0$,即$s_{l-1} < s_{r}$,這就變得和上一題一樣,當固定了右端點$r$後,要在$r$的左邊找到一個滿足$s_{l-1} < s_{r}$,同時為最小的$l-1$。同樣是在小於$val$的數中找到最小下標這個模型。
AC程式碼如下,時間複雜度為$O(n \log{n})$:
1 class Solution { 2 public: 3 int longestESR(vector<int>& sales) { 4 int n = sales.size(); 5 vector<int> s(n + 1); 6 for (int i = 1; i <= n; i++) { 7 s[i] += s[i - 1] + (sales[i - 1] > 8 ? 1 : -1); 8 } 9 10 int ret = 0; 11 vector<int> stk; 12 for (int i = 1; i <= n; i++) { 13 if (stk.empty() || s[i - 1] < s[stk.back()]) stk.push_back(i - 1); 14 int l = 0, r = stk.size() - 1; 15 while (l < r) { 16 int mid = l + r >> 1; 17 if (s[stk[mid]] < s[i]) r = mid; 18 else l = mid + 1; 19 } 20 if (s[stk[l]] < s[i]) ret = max(ret, i - stk[l]); 21 } 22 23 return ret; 24 } 25 };
線段樹和樹狀陣列實現的AC程式碼如下,時間複雜度均為$n \log{n}$:

const int N = 2e4 + 10; class Solution { public: struct Node { int l, r, minv; }tr[N * 4]; vector<int> s; void build(int u, int l, int r) { if (l == r) { tr[u] = {l, r, N}; } else { int mid = l + r >> 1; build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); tr[u] = {l, r, N}; } } void modify(int u, int x, int c) { if (tr[u].l == x && tr[u].r == x) { tr[u].minv = min(tr[u].minv, c); } else { if (x <= tr[u].l + tr[u].r >> 1) modify(u << 1, x, c); else modify(u << 1 | 1, x, c); tr[u].minv = min(tr[u << 1].minv, tr[u << 1 | 1].minv); } } int query(int u, int l, int r) { if (tr[u].l >= l && tr[u].r <= r) return tr[u].minv; int mid = tr[u].l + tr[u].r >> 1, ret = N; if (l <= mid) ret = query(u << 1, l, r); if (r >= mid + 1) ret = min(ret, query(u << 1 | 1, l, r)); return ret; } int longestESR(vector<int>& sales) { int n = sales.size(); s = vector<int>(n + 1); for (int i = 1; i <= n; i++) { s[i] += s[i - 1] + (sales[i - 1] > 8 ? 1 : -1); } build(1, -n - 1, n); // 值域是[-(n+1), n],查詢的時候s[i]還要減1 int ret = 0; for (int i = 1; i <= n; i++) { modify(1, s[i - 1], i - 1); ret = max(ret, i - query(1, -n - 1, s[i] - 1)); } return ret; } };
其中值域的範圍是$[-n,n]$,對於樹狀陣列需要將整個值域對映到正整數區間,因此可以對區間整體加上$n+1$,這樣就可以對映到$[1, 2n+1]$了。

const int N = 2e4 + 10; class Solution { public: int n; int tr[N]; vector<int> s; int lowbit(int x) { return x &-x; } void add(int x, int c) { for (int i = x + n + 1; i <= n << 1; i += lowbit(i)) { tr[i] = min(tr[i], c); } } int query(int x) { int ret = N; for (int i = x + n + 1; i; i -= lowbit(i)) { ret = min(ret, tr[i]); } return ret; } int longestESR(vector<int>& sales) { n = sales.size(); s = vector<int>(n + 1); for (int i = 1; i <= n; i++) { s[i] += s[i - 1] + (sales[i - 1] > 8 ? 1 : -1); } memset(tr, 0x3f, sizeof(tr)); int ret = 0; for (int i = 1; i <= n; i++) { add(s[i - 1], i - 1); ret = max(ret, i - query(s[i] - 1)); } return ret; } };
參考資料
AcWing 4487. 最長連續子序列(AcWing杯 - 周賽:https://www.acwing.com/video/4001/
