數值分析<3>——任意曲線擬合

全文目錄

萬物皆是展開式

你是否想過這樣一個問題，任何的函數，也許都能通過一個「大一統」理論將他們整合在一起。事實上對於任意一種對應關係，我們都能找到一個函數儘可能去貼合它，我們採取的是一種極限的思維，舉個不恰當的例子來描述，如果一個東西看起來像牛糞，聞起來像牛糞，嚐起來像牛糞，那麼它就是牛糞。並且，更加一般的是，在一個微小的區間內，函數還可以寫成一個冪函數的形式去大致的估算。

泰勒定理給了我們一個很通用的方法去研究函數：

設n是一個正整數。如果定義在一個包含a的區間上的函數\(f\)在a點處n+1次可導，那麼對於這個區間上的任意x，都有：

\[f(x)=\sum^{n}_{i=0}\frac{f^{(i)}(a)}{i!}(x-1)^i+R_n(x) \]

其中，上式的\(R_n(x)\)是泰勒公式的估計餘項，這在後續會進行詳細的解釋。

如果僅僅只是背下來，你就不能領略到泰勒展開的精妙之處了。我們用一些很精妙的手段，自然的推匯出泰勒公式。首先我們先假定一個函數存在一階導函數，來看一看一階導數的定義

\[\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=f^{'}(x_0) \]

其實從這裡不難發現，導數定義上，給了我們一種當\(x\to x_0\)的時候，計算\(f(x)\)的手段，我們假定這個過程的無窮小為\(\alpha(x)(x\to x_0)\)，那麼我們可以把這個等式改寫為如下形式

\[\lim_{x\to x_0} = f(x) = L \Leftrightarrow f(x) = L+\alpha(x) \\ \\ \lim_{x\to x_0}f^{'}(x) = \frac{f(x)-f(x_0)}{x-x_0} = f^{'}(x)+\alpha(x) \\ \\ f(x) = f(x_0)+f^{'}(x_0)(x-x_0)+\alpha(x)\times(x-x_0) \\ \\ =f(x_0)+f^{'}(x_0)(x-x_0)+\omicron(x-x_0) \]

餘項估計

從上面的推導規程很明顯可以看出最後一項無窮小是\((x-x_0)\)的高階無窮小，所以我們就很自然的得出了\(f(x)\)的一階泰勒展開式。利用這個公式，我們可以去擬合任意可導的函數的任意函數點，再從點的繪製成函數曲線。

當然我們會認為，一階導數所帶來的那個餘項無窮小是不夠精確的，提高精確值的方法就是讓這個無窮小的階升高，那麼我們可以繼續考慮二階展開，讓這個無窮小的階數升高。首先我們來單獨的研究一下這個無窮小。

\[\omicron(x-x_0) = f(x)-f(x_0)-f^{'}(x_0)(x-x_0) \\ \\ \lim_{x\to x_0}\frac{\omicron(x-x_0)}{(x-x_0)^2} = \lim_{x\to x_0}\frac{f(x)-f(x_0)-f^{'}(x_0)(x-x_0)}{(x-x_0)^2} \]

很明顯，只要我們的函數二階可導，那麼上述式子就滿足了0/0型的洛必達法則！那麼我們直接開始洛必達！

\[\lim_{x\to x_0}\frac{f(x)-f(x_0)-f^{'}(x_0)(x-x_0)}{(x-x_0)^2} = \lim_{x\to x_0}\frac{f^{'}(x)-f^{'}(x_0)}{2(x-x_0)} \\ \\ =\frac{1}{2}f^{''}(x_0) = \lim_{x\to x_0}\frac{\omicron(x-x_0)}{(x-x_0)^2} \Leftrightarrow \omicron(x-x_0) = \frac{1}{2}f^{''}(x_0)(x-x_0)^2 \\ \\ \Leftrightarrow f(x) = f(x_0)+f^{'}(x_0)(x-x_0)+\frac{1}{2}f^{''}(x_0)(x-x_0)^2 +\omicron(x-x_0)^2 \]

這樣，我們就得到了擁有二階無窮小的泰勒公式！如法炮製，只要我們的\(f(x)\)在\(x_0\)滿足n階可導的情況，那麼我們就可以一直用上面的方式得到n階泰勒展開公式。

接下來我們來估計餘項，也就是誤差的大小。在上面的推斷中，我們一直使用無窮小進行誤差的估計，這種型別的餘項叫做皮亞諾餘項，這種好處是可以很直觀的看出誤差的階數，但是並不算是一個特別容易計算的值，我們僅僅知道最大的誤差不超過\(\omicron(x-x_0)^n\)。因此我們可以思考一下，假如我們展開到第n階的時候，誤差必然是比第n+1階新引入的那一項更大，但比第n階是更小的，那麼我們可以用介值定理和拉格朗日微分中值定理進行推廣，那麼餘項可以寫成

\[R_n(x) = \frac{f^{(n+1)}(\theta)}{n!}(x-x_0)^{n+1} \]

利用泰勒公式，我們就可以將一個可導函數的任意點進行一個擬合，從而得到一個較為精確的結果，從函數影象上看，泰勒公式是一個級數累加不斷前進逼近的過程。

多項式插值法

如果針對的是一個有窮數列，例如請你尋找以下數位的規律並填寫接下來的數位

4、7、11、18、29、47、(__)

你的第一眼可能會發現這是一個類似 Fibonacci數列的規律數位，但實際上我們對於有窮離散型函數，也可以推出這樣一個奇怪的對應關係

\[a_x=\frac {28579 x^9}{90720} - \frac{142847 x^8}{10080} + \frac{4140931 x^7}{15120} \\- \frac{713627 x^6}{240} + \frac{17192243 x^5}{864} - \frac{40631363 x^4}{480} \\+ \frac{644406697 x^3}{2835} - \frac{927568429 x^2}{2520} +\frac {101426987 x}{315} - 113739 \]

並且對於任何的有窮的數列，我們總是能使用一個通項公式進行資料的擬合計算。如果我們把上述拓展到函數領域，也就是對於任意有限多的\((x_i,y_i)\)，且這些點符合函數的規則，每個x對應唯一的y，我們總能用一個連續的多項式組合的函數，保證這個函數經過上面所有的點，而計算這個多項式的過程，我們就稱為插值。插值是求值的逆過程，利用已有的點，反推出曲線的大致模樣。

插值的思想和泰勒很類似，就是說如果觀測誤差足夠小的時候，那麼就認為它就是準確的值。我們給定的點符合\(f(x_i)=y_i\)，那麼我們的插值建構函式就是\(g(x_i)=y_i\)。

通常我們採用累加的多項式進行插值計算，因為我們的計算都是建立在計算機之上，計算機對於特殊的運算是非常緩慢且複雜的，例如之前提到的泰勒展開，因此我們儘可能需要將計算變成四則運算，同時我們的插值函數還需要保證解的唯一性，因此我們通常將插值函數寫成如下形式：

\[P(x) = \sum_{i=0}^{n}a_{i}x^{i} \]

利用多項式冪函數和作為插值函數的好處是，它是恆可微的，並不需要像泰勒展開一樣，需要先確定可微分的函數才可以繼續求解。同時至於這種方式的唯一性，我們可以做一個簡單的推導。

假設給定了n+1個資料取樣\((x_1,y_1),(x_2,y_2)\dotsb(x_{n+1},y_{n+1})\)，根據插值法的規則，那麼我們構造出的多項式必然滿足下列方程組：

\[\left\{\begin{matrix} p(x_0) = a_0+a_1x_0+a_2x_{0}^2+\dotsb+a_nx_{0}^n = y_0 \\ p(x_1) = a_0+a_1x_1+a_2x_{1}^2+\dotsb+a_nx_{1}^n = y_1 \\ p(x_2) = a_0+a_1x_2+a_2x_{2}^2+\dotsb+a_nx_{2}^n = y_2\\ \vdots \\ p(x_n) = a_0+a_1x_n+a_2x_{n}^2+\dotsb+a_nx_{n}^n = y_n \end{matrix}\right. \]

如果熟悉線性代數，我們可以很清楚的發現這是一個非齊次線性方程組（a為未知數），我們可以得到該方程組的\(Vandermonde\)行列式

\[P = VA=Y \Leftrightarrow \begin{bmatrix} 1 & x_0&x_{0}^{2} &\cdots & x_{0}^{n} \\ 1 & x_1&x_{1}^{2} &\cdots & x_{1}^{n} \\ \vdots&\vdots&\vdots&\vdots&\vdots\\ 1 & x_n&x_{n}^{2} &\cdots & x_{n}^{n} \end{bmatrix} \begin{bmatrix} a_0\\ a_1\\ \vdots\\ a_n \end{bmatrix}= \begin{bmatrix} y_0\\ y_1\\ \vdots\\ y_n \end{bmatrix} \]

故有

\[\begin{vmatrix}V\end{vmatrix} = \begin{vmatrix} 1 & x_0&x_{0}^{2} &\cdots & x_{0}^{n} \\ 1 & x_1&x_{1}^{2} &\cdots & x_{1}^{n} \\ \vdots&\vdots&\vdots&\vdots&\vdots\\ 1 & x_n&x_{n}^{2} &\cdots & x_{n}^{n} \end{vmatrix} = \prod_{i=1}^{n}\prod_{j=0}^{n}(x_i-x_j) \]

因為我們取得取樣點都是不同的點，因此可以保證有\(x_i \neq x_j\)，那麼根據\(Cramer\)法則，該\(Vandermonde\)行列式必有唯一解，從而保證了我們的插值函數是唯一的。不過多項式插值也不是全無缺點的，計算複雜度較高、在端點出容易出現龍格現象（一種函數值的劇烈振盪）。這些問題我們將在後面進行討論。

拉格朗日插值法

拉格朗日插值是一種樸素擬合的手段，假設我們給定n個資料點\((x_1,y_1),(x_2,y_2)\dotsb(x_n,y_n)\)，拉格朗日插值法，就是構造一條經過這些點的曲線（如果本身的資料就存在大量誤差，則只需要靠近而不需經過），用這條線去模擬實際的曲線。這個方法和我們通過兩點構造一條直線的方法有異曲同工之妙，當我們代入一個值\(x_1\)之後，所有不能得到\(y_1\)的多項式都將係數為0。

一次線性插值

我們先從最容易的一次線性插值來入手，假設我們有曲線\(f(x_i) = y_i\)，取兩個取樣點\(x(x_0,y_0),(x_1,y_1)\)，我們一次線性插值則是使用一條直線來近似替代，那麼我們需要構建一個函數，使得\(p(x_0)=y_0,p(x_1)=y_1\)，那麼可以作出這樣一條直線（直線對稱式）：

\[p(x) = \frac{x-x_0}{x_0-x_1}y_0+\frac{x - x_1}{x_1-x_0}y_1 \]

我們看一個簡單的函數擬合，已知\(y=\sqrt{x}\)的兩個取樣點\((100,10),(121,11)\),求\(\sqrt{115}\)，我們利用線性插值法，可以計算出結果是10.7142，精確值為10.724，可見利用線性插值也具備三位有效數位。但是如果將值偏離取樣點，例如我們需要計算\(\sqrt{2}\)，精確值為1.414，而插值法計算出的值為5.333，一位有效數位都沒有。

實際上我們利用資訊的角度去考慮，比如在警察辦案過程中，往往會涉及到一個犯罪嫌疑人畫像的製作，如果說目擊者告訴警察的有效資訊為：犯罪分子是一個高鼻樑，藍眼睛。那麼警察在繪製影象的時候，眼睛和鼻子或者周邊的顴骨可能會相對精確不少，但是通過鼻子和眼睛的資訊，你讓警察去猜想他是否是禿頂或者升高體重，自然會不準確。所以這裡面也涉及到了一部分資訊熵的內容，因為資訊過少而導致的資料不精確。

拉格朗日插值

通過一次插值的實踐過程和之前對於多項式插值的，我們知道取樣點很少導致的資訊缺失，那麼我們就應該找到更多的取樣點進行構造更好的多項式。

根據觀察，其實我們可以思考一下，之前多項式插值法中，我們最終是需要通過行列式解出各個多項式的係數，那麼我們假定為這樣的插值函數

\[p(x)=\sum_{i=0}^{n}l_i(x)y_i \]

我們將多項式係數寫為\(l(x)\)我們稱為拉格朗日插值基函數。這個基函數必然滿足

\[p(x_i)=y_i \\ l_i(x_k) =\begin{cases} 0,& k\neq i\\ 1,& k=0 \end{cases} \]

通過這個我們很容易分析出插值基函數\(l_i(x)\)有零點\(x_i\)，其他的均為非零點，那麼我們假設插值基函數為：

\[l_i(x) = C\prod_{k=0,k\neq i}^n (x-x_k) \]

同時因為\(l_i(x_i)=1\)可以繼續確定常係數

\[C = \frac{1}{\prod_{k=0,k\neq i}^n (x_i-x_k)} \]

因此我們得到了我們的插值基函數和我們的插值擬合函數

\[l_i(x)=\prod_{k=0,k\neq i}\frac{x-x_k}{x_i-x_k} \\ p_n(x) = \sum_{i=0}^{n}l_i(x)y_i = \sum_{i=0}^{n}(\prod_{k=0,k\neq i}^n\frac{x-x_k}{x_i-x_k})\times y_i \]

因此，我們可以編寫出一程式，作為我們拉格朗日插值法的

double[] Lagrange(double[]x,double[] y,double[] xi)
{
    double[] result = new double[xi.Length];
    if (x.Length != y.Length)
    {
        throw new ArgumentException("dim x not equal dim y");
    }
    int n = x.Length;
    for (int k = 0; k < xi.Length; k++)
    {
        double value = 0;
        for (int i = 0; i <n; i++)
        {
            double mulValue = 1;
            for (int j = 0; j < n; j++)
            {
                if (i == j)
                    continue;
                mulValue = mulValue * (xi[k] - x[j]) / (x[i]- x[j]);
            }
            value += mulValue * y[i];
        }
        result[k] = value;
    }
    return result;
}

更有matlab、python版本的程式碼在倉庫中可以對照使用。倉庫地址見文章開頭

*拉格朗日插值餘項

既然是擬合，總歸是有誤差的，接下來我們研究一下最終的誤差。對於拉格朗日插值法，誤差實際上是一個階段誤差\(R(x) = f(x) - p(x)\)，根據之前我們推匯出的拉格朗日插值函數，誤差餘項記為\(R(x) = f(x) - p(x)\)。

那麼我們作一輔助函數如下

\[\varphi(t) = f(t)-p(t)-\frac{g(t)}{g(x)}[f(x)-p(x)]\\ g(x)=\prod_{i=0}^n(x-x_i) \]

容易發現\(g^{n+1}(t) = (n+1)!\)，而插值函數只有n階，故\(p^{n+1}(t) = 0\)，因此我們構造的輔助函數是連續且具有n+1階導數。當\(t=x\)時，則會有\(\varphi(t)=0\)，根據Rolle定理，則必有以下：

當\(\varphi(t)\)在插值區間內有n+2個互異零點時，則一階導數至少有n+1個互異零點
當\(\varphi^{(1)}(t)\)在插值區間內有n+1個互異零點時，則\(\varphi^{(2)}(t)\)至少有n個互異零點

以此類推，容易知道\(\varphi^{(n)}(t)\)有2個零點時，則\(\varphi^{(n+1)}(t)\)至少有一零點，設此零點為\(t=\xi\)，對\(\varphi(t)\)求n+1次導數後，有

\[\varphi^{(n+1)}(\xi) = f^{(n+1)}(\xi)-\frac{(b+1)!}{g(x)}[f(x)-p(x)]=0 \]

故我們插值的截斷誤差為\(f(x)-p(x) = \frac{f^{n+1}(\xi)}{(n+1)!}\prod_{i=0}^{n}(x-x_i)\)，其中\(\xi\)取決於我們需要預測的值。自此，我們得到了拉格朗日插值法的所有內容。

Newton差商插值

拉格朗日插值多項式的得出並不容易，至少在計算機眼中，他是複雜的，需要計算多個n-1階的多項式。同時，這裡我們給出一個定理：所有的插值多項式和拉格朗日插值多項式的結果應當是相同的，只是以不同的方式計算和書寫。。

差商

首先我們介紹以下差商的概念，實際差商是一個很簡單的東西，定義如下：假設順序排列的節點\(x_0,x_1,\dotsb,x_n\)對應函數值為\(f(x_0),f(x_1),\dotsb,f(x_n)\)，那麼一階差商為

\[f[x_0,x_k]=\frac{f(x_0)-f(x_k)}{x_0-x_k},(1<=k<=n) \]

二階差商為

\[f[x_0,x_1;x_2,x_k]=\frac{f[x_0;x_1,x_2]-f[x_0;x_1,x_k]}{x_2-x_k},(2<=k<=n) \]

那麼K階差商為：

\[f[x_0,x_1,\dotsb;x_{k-2},x_{k-1}]=\frac{f[x_0,x_1\dotsb;x_{k-2},x_{k-1}]-f[x_0,x_1\dotsb x_{k-2},x_{k}]}{x_{k-1}-x_k},(k<=n) \]

k階差商亦可寫成

\[f[x_0,x_1,\dotsb,x_{k-1},x_{k}] = \frac{f[x_0,x_1,\dotsb,x_{k-1}]-f[x_0,x_1,\dotsb,x_{k-1},x_{k}]}{x_0-x_k} \]

實際上就是個遞推的公式，看起來似乎很複雜，但實際上自己嘗試去計算的時候會發現，是一個很簡單的東西，同時差商是函數的一個線性組合，這又可以說到線性代數了，我們假設組合出的多項式是一個類似座標的玩意，而每一階的差商實際上就是向量的基，因此通過差商，我們可以表示出多項式空間中任一多項式。

牛頓差商公式

牛頓差商公式就是將我們的差商做出組合：

\[P(x) = f[x_1]+f[x1,x2](x-x_1)+f[x_1,x_2,x_3](x-x_1)(x-x_2)+\dotsb+f[x_1\dotsb x_n](x-x_1)\dotsb (x-x_{n-1}) \]

隨便給出幾個插值取樣點，進行計算拉格朗日和牛頓插值公式，我們在計算出各階差商以後，會發現最終得到的插值多項式和拉格朗日多項式是一致的。那我們為什麼還需要多此一舉引入牛頓法進行插值而不是直接使用拉格朗日插值呢？

答案很簡單，拉格朗日法在構建多項式時，我們必須先知道取樣點的數量，如果後續有了新的取樣點，我們就需要重新計算整個多項式，這是對於效能浪費極大的。如果採用牛頓法，那麼在有新的取樣點時，我們只需要多計算一次差商（因為之前的差商已經計算好），可以很容易的將新的點加入我們的多項式中。

牛頓法的程式碼如下（更多程式碼見倉庫）

double Newton(double[] x, double[] y,double xi)
{
    if (x.Length != y.Length)
    {
        throw new ArgumentException("dim x not equal dim y");
    }
    int n = x.Length;
    double[,] args = new double[n,n];
    for (int i = 0; i < n; i++)
    {
        args[i,0] = y[i];
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = i; j <= n; j++)
        {
            args[j,i] = (args[j - 1,i - 1] - args[j,i - 1]) / (x[j - i] - x[j]);
        }
    }
    double result = y[0];
    for (int i = 1; i < x.Length; i++)
    {
        double mulValue = 1.0;
        for (int j = 0; j < i - 1; j++)
        {
            mulValue = mulValue * (xi - x[j]);
        }
        result += args[i, i] * mulValue;
    }
    return result;
}

插值餘項

實際上，牛頓法因為得到的結果和拉格朗日插值一樣，他們的誤差也應該是一樣的，不過既然我們選擇了不同的計算方法，那麼誤差也可以使用新的手段進行計算。如果我們把我們的插值點看作一固定點，帶入我們的差商公式，依次遞推，會得到最後的插值餘項。

\[R(x) = f[x_0,x_1\dotsb,x_n,x](x-x_0)(x-x_1)\dotsb(x-x_n) \]

高次插值的Runge(龍格)現象

在多項式插值以及基於多項式插值的拉格朗日插值方法和含有高次冪的牛頓插值中，我們提到過龍格現象，那麼什麼是龍格現象呢？首先我們先提出這樣一個問題，當我們在拉格朗日多項式之中提高項數和多項式的次數，是否可以提高我們資料的精度？這個答案是否定的，我們需要減少誤差，也就是說針對任意的\(\epsilon>0\)，總是存在正整數N，當n大於N時，所有區間內的\(x\)滿足:

\[f(x)-p_n(x)<\epsilon \Leftrightarrow \frac{f^{n+1}(\xi)}{(n+1)!}\prod_{i=0}^{n}(x-x_i)<\epsilon \]

我們可以看到，我們的誤差，隨著n的增大，(n+1)!逐漸趨於無窮，而後向的乘法，並不會增大太多會變小太多，因此誤差很大程度取決於n+1階導數的範圍。對於類似\(sinx,e^x\)，這類導數的值域範圍恆定的函數，誤差會隨著n的增加逐步趨於0。但是如果對於某些函數而言，隨著項數次數增加，誤差反而會變大。龍格現象是一種出現在多項式次數很高是，在區間端點出現擬合曲線劇烈振盪的一種現象。下面通過一個例子來進行說明。

假設給定\(f(x) = \frac{1}{x^2+1},x\in [-5,5]\)，等距離取5，10個點，構建多項式擬合，觀察影象。

我們可以很清楚的發現，當靠近端點的時候。擬合曲線出現了劇烈的波動，誤差到了一個不太可以接受的程度。並且次數越高的時候，抖動出現的更頻繁、更劇烈。龍格現象的出現是由於插值節點是等距所造成的。同時，針對導函數不穩定的函數而言，盲目增加插值節點數列，則更加容易出現龍格現象。

一般而言，為了避免龍格現象，我們可以有以下的手段：

避免使用高次的插值多項式，一般而言，即使為了提高插值精度，也儘可能保證\(n<7\)。
分段進行插值，在每一小段使用一次插值，從而降低階數。
對於性態不穩定的函數，選用其他插值手段，如Hermite插值等。

Hermite插值

在之前的插值方法中，我們的要求僅僅是在滿足\(f(x)=p(x)\)或者兩者足夠接近作為一個條件，但是這並不足以做出完美的擬合，在許多時候，我們往往還會要求導數及高階導數儘可能相同或接近，這種拓展了條件的插值方法，就是我們的Hermite插值方法。

最常見的是我們通常會要求曲線的一階導數接近或相同，這樣可以保證我們曲線的一個平滑效能。那麼假設曲線\(y=f(x)\)，一階導數為\(y^{'} = f^{'}(x)\)，那麼Hermite插值需要保證：

\[\begin{cases} H(x_i) = y\\ H^{'}(x_i) = y^{'} \end{cases} \]

不難發現，我們不僅要求了相等的條件，更是要求了相切的條件，因此上述公式具有2(n+1)個取樣點（曲線和曲線導數各一半）,那麼我們仿造拉格朗日插值條件。可以構造一個這樣的插值多項式：

\[H(x) = a_0(x)y_0 + b_0(x)y^{'}_0 + \dotsb + a_n(x)y_n + b_n(x)y^{'}_n = \sum_{i=0}^{n}(a_i y_i + b_i y^{'}_i) \]

其中，需要滿足：

\[\begin{cases} a_i(x_k)= \begin{cases} 0,k \neq i \\ 1,k=i \end{cases}\\ a^{'}_i(x_k)= 0 \end{cases} \]

\[\begin{cases} b_i(x_k)= \begin{cases} 0,k \neq i \\ 1,k=i \end{cases}\\ b^{'}_i(x_k)= 0 \end{cases} \]

接下來我們用比較長的篇幅證明推導以下我們的Hermite插值的基函數\(a(x),b(x)\)，以及證明他的唯一性。

首先我們來求\(b(x)\)，它需要滿足

\[b_i(x_k) = b^{'}_i(x_k) = 0 , i \neq k \\ \]

易知滿足上述條件的該點為二重根，所以必有因子\((x-x_i)^2 ,i \neq k\)，

\[b_i(x_k) = 0, b^{'}_i(x_k) = 1 , i = k \\ \]

易知滿足上述條件的該點為單根，因此還會有另一個因子，\((x-x_i) ,i=k\)。又因為b(x)是次數不超過2n+1的多項式，根據拉格朗日多項式的定義，可以假定

\[b_i(x) = C(x-x_i)l_i^{2}(x) \]

上述式子滿足我們之前的規定，同時因為\(b^{'}_i(x) = 1\)，可以輕鬆的確定常係數為1。故\(b_i(x) = (x-x_i)l_i^{2}(x)\)。接下來可以確定一下\(a(x)\)。

同樣的，因為\(a(x)=0,a^{'}_i(x)=0,i\neq k\)說明也具有二重根，同樣基函數會含有\(（x-x_i)^2,i\neq k\)，但略微不同的是，\(k=i\)的時候，P我們不能在獲得任何因子湊夠2n+2項。因此我們利用待定係數法假定基函數為

\[a_i(x)= (ax+b) l_i^{2}(x) \]

同樣代入我們的條件，最終可以求得：

\[a_i(x) = (1-2(x-x_i)\sum_{k=0,k\neq i}^{n}\frac{1}{x_i-x_k})l^{2}_i(x) \]

最後我們證明一下我們得到的插值多項式是唯一的，我們利用反證法：

假設存在另一個\(h(x)\)是滿足Hermite插值條件，那麼設：

\[\varphi(x) = H(x) - h(x) = 0\\ \varphi^{'}(x) = H^{'}(x_i) - h^{'}(x_i) = 0 \]

由於有n+1個i，因此\(\varphi(x)\)有2n+2個零點，但是\(\varphi(x) = H(x) - h(x) = 0\)次數不超過2n+1，所以\(\varphi(x) = 0\)，因此\(H(x) = h(x)\)，該多項式唯一。

Hermite插值餘項

若我們的函數\(f(x)\)在插值區間上2n+2階導數，那麼我們假設餘項為\(R(x) = f(x)-H(x)\)，由Hermite插值定義可知，\(x_i\)是\(R(x)\)的二重根，因此\(R(x)\)含有\((x-x_i)\)，那麼設

\[R(x) = k(x)\prod_{i=0}^{n}(x-x_i)^2 \]

做出輔助函數

\[\varphi(x) = f(t)-H(t) - R(x) \]

根據定義易知

\[\varphi(x_i) = 0,\varphi^{'}(x_i) = 0,\varphi(x) = 0 \]

因此輔助函數至少有n+1個二重零點x_i，以及零點x，根據羅爾定理，容易知道在每兩個二重零點之間都有一個零點，同時\(\varphi^{'}(x_i) = 0\)，\(\varphi^{'}(t)\)至少有2
n+2個零點，以此類推，那麼有

\[\varphi^{(2n+2)}(\xi) = f^{(2n+2)}\xi)-(2n+2)!k(x)\\ k(x) = \frac{f^{(2n+2)}\xi)}{(2n+2)!} \]

所以餘項公式為：

\[f(x) = \frac{f^{(2n+2)}\xi)}{(2n+2)!}\prod_{i=0}^{n}(x-x_i)^2 \]

Hermite的程式碼如下（更多程式碼見倉庫）

Chebyshev插值

我們之前談論的插值函數通常取樣點是一個平均分佈的取樣點，比如說我們一個實際的例子，我們需要採集子彈發射速度，我們往往會使用等間隔時間發射一顆子彈。但是往往等間隔這件事情本身就是有難度的，也就是說我們選取的點對結果是有影響的，如下圖，在端點的時候，誤差可能會達到一個無窮大的地步。切比雪夫插值就是採用最優點間距選取的插值方法。

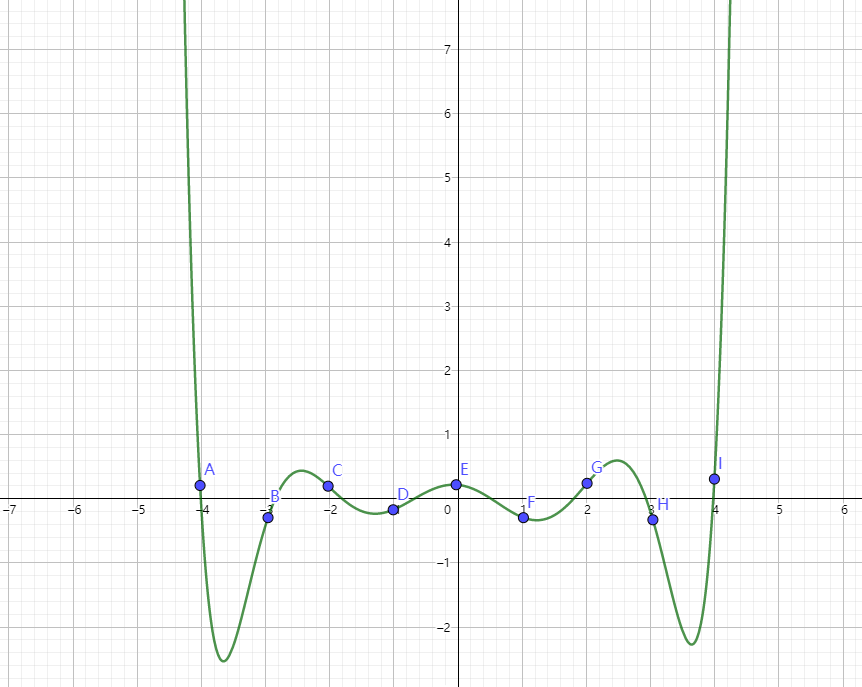
切比雪夫插值的出發點就是在插值區間上，控制插值誤差的上下界，即

\[\frac{\prod^{n}_{1}(x-x_i)}{n!}f^(n)(\xi) \]

將這個誤差控制在絕對值為1以內，實際上這是一個關於x的多項式，那麼我們的問題就是，這個多項式是否存在極值，是否有特定的\(x_i\)使得最大值足夠的小呢？那麼我們試著列出公式進行推導：

\[\min{(\max_{1\leqslant x\leqslant 1}\left|\prod_{i=1}^{i=n}(x-x_i)\right|)} \]

我們再考慮一個問題，我們既然要構造多項式，並且控制誤差在1以內，那麼考慮一下三角函數，因為三角有兩個優秀的性質：

三角函數的值域在\([-1,1]\)
根據傅立葉展開，我們知道曲線可以用三角函數進行擬合

因此如果區間在\([-1,1],\)我們選擇\(x_i = cos\frac{(2i-1)\pi}{2n}\)（如果區間為[a,b]，那麼選取\(x_i = \frac{b+a}{2} + \frac{b-a}{2}cos\frac{(2i-1)\pi}{2n}\)），這樣\(x_i\)最小值就是\(1/2^{n-1}\)。我們可以看看切比雪夫根構造的插值取樣點和普通的插值取樣點構造的函數有何區別：

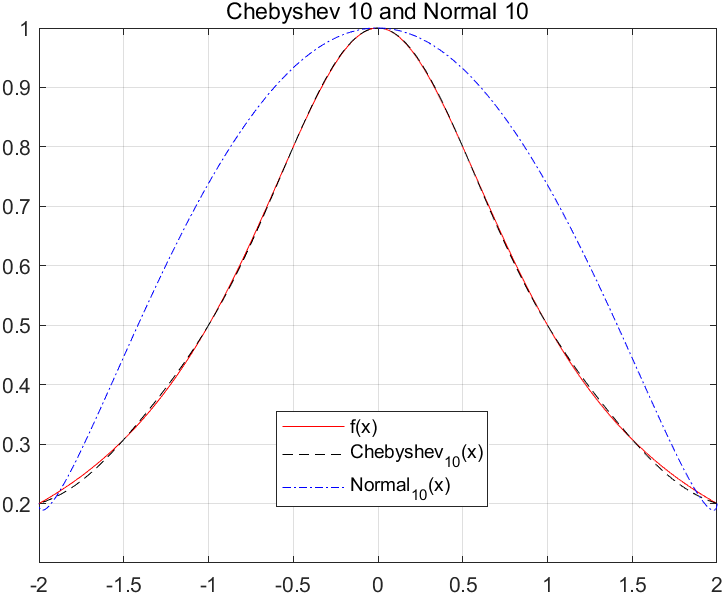
我們利用切比雪夫根（建議學習切比雪夫微分方程），構造的多項式就是切比雪夫多項式，在此之前，我們看一看三角函數的展開：

\[cos(2\theta) = 2cos^2\theta-1\\ cos(3\theta) = 4cos^3\theta-3cos\theta\\ cos(4\theta) = 8cos^4\theta-8cos^2\theta+1\\ \]

通過觀察，那麼我們假設\(g(cos\theta) = cosn\theta\)，\(g(x)\)是一個多項式，係數為\(2^{n-1}\)。實際上這也是成立的，證明過程留給讀者。那麼我們令切比雪夫多項式公式為：\(g_n(cos\theta) = cosn\theta\)
，於是：

\[g_{n+1}(cos\theta) = cos(n\theta+\theta) = cosn\theta cos\theta-sinn\theta sin\theta \\ g_{n-1}(cos\theta) = cos(n\theta-\theta) = cosn\theta cos\theta+sinn\theta sin\theta \]

可以發現

\[g_{n+1}(cos\theta)+g_{n-1}(cos\theta) = 2cosn\theta cos\theta = 2cos\theta g_{n}(cos\theta) \\ \Rightarrow g_{n+1}(x) = 2xg_n(x) - g_{n-1}(x) \]

我們就得到了切比雪夫多項式的遞推公式。切比雪夫插值的程式碼如下：

兩種曲線的擬合與預測

我們之前往往要求插值曲線嚴格的經過各個插值取樣點，這個方式往往具有不可操控的地方。例如我們的取樣點往往也只是一個粗略的估計，如果我們強行使插值曲線通過這些點，那麼資料本身的誤差也會反映在資料之中，例如下圖中，使用一條直線去擬合獲得的誤差理論上要比經過這些點的曲線更加優秀。因此我們需要使用某種方式進行限制，這裡我們介紹三種擬合方式。

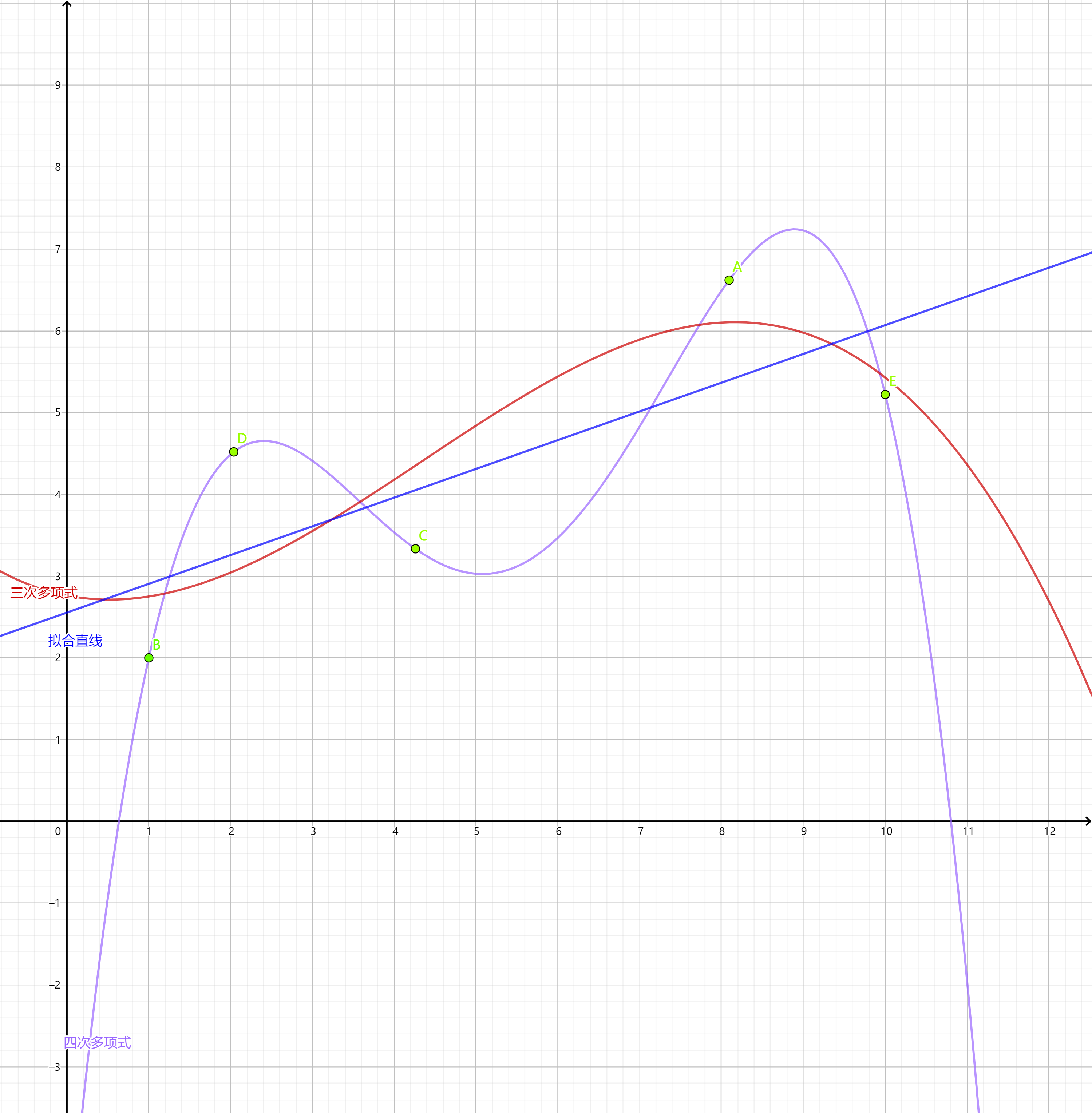
直線擬合法

直線擬合是最為簡單的擬合方法，也就是構造一套直線\(y=ax+b\)，使得我們的取樣點近似的接近這條直線，我們有三種方式進行衡量擬合的優劣

準則一：使得誤差最大絕對值最小
準則二：使得總誤差的絕對值最小
準則三：使得誤差平方和最小

其中準則三就是我們介紹的最小二乘法，我們就以準則三構造擬合的直線，那麼設取樣點有\((x_i,y_i),i\in n\)，那麼總誤差為：

\[Min(Q)=\sum_{i=1}^{n}e_i^2 = \sum_{i=1}^{n}[y_i-g(x_i)]^2 = \sum_{i=1}^{n}[y_i-(ax_i+b)]^2 \]

容易發現我們的誤差Q是關於a,b的函數，因此這裡我們可以使用二元函數求導法則求得引數值。

\[\frac{\partial Q}{\partial a} = -2\sum_{i=1}^{n}x_i(y_i-ax_i-b) = 0\\ \frac{\partial Q}{\partial b} = -2\sum_{i=1}^{n}(y_i-ax_i-b) = 0\\ \Rightarrow \sum_{i=1}^{n}y_i = a\sum_{i=1}^{n}x_i + nb\\ \sum_{i=1}^{n}x_iy_i = a\sum_{i=1}^{n}x_i^2 + b\sum_{i=1}^{n}x_i \]

聯立上述式子可以解出a與b：

\[a = \frac{(\sum_{i=1}^{n}x_i^2)(\sum_{i=1}^{n}y_i)-(\sum_{i=1}^{n}x_iy_i)(\sum_{i=1}^{n}x_i)}{n\sum_{i=1}^{n}x_i^2-(\sum_{i=1}^{n}x_i)^2} \\ b = \frac{n(\sum_{i=1}^{n}x_iy_i)-(\sum_{i=1}^{n}x_i)(\sum_{i=1}^{n}y_i)}{n\sum_{i=1}^{n}x_i^2-(\sum_{i=1}^{n}x_i)^2} \]

採用直線擬合法，則需要保證取樣點大致像直線的分佈，或者說均勻分佈在直線兩側，如果不符合這個則儘量不使用直線擬合。

指數擬合

對於某些增長型的曲線，我們可以採用指數函數\(y=ae^{bx}\)進行擬合，雖然是指數函數，我們可以將它化為直線方程，如下：

\[lny = lna + bx,\\ Y = lny,B = b,lna = A \Rightarrow Y = A+BX \]

利用這個方程，我們可以利用直線擬合的手段，確定係數。不過檢驗我們的擬合精度的指標略微不同，指標為：

誤差總平方和儘可能小
標準差\(\sigma = Q/(n+2)\)
相關係數\(R = 1- \frac{\sum(\tilde{y}-y_i)^2}{\sum(y_i-y)^2}\)，R儘可能接近1

習題

Reference

《數值分析》（原書第二版） —— Timothy Sauer

《數值計算方法》（清華大學出版社） —— 呂同富等

About Me

作　　者：WarrenRyan
出　　處：https://www.cnblogs.com/WarrenRyan/
本文對應視訊：BiliBili
關於作者：熱愛數學、熱愛機器學習，喜歡彈鋼琴的不知名小菜雞。
版權宣告：本文版權歸作者所有，歡迎轉載，但未經作者同意必須保留此段宣告，且在文章頁面明顯位置給出原文連結。若需商用，則必須聯絡作者獲得授權。
特此宣告：所有評論和私信都會在第一時間回覆。也歡迎園子的大大們指正錯誤，共同進步。或者直接私信我
聲援博主：如果您覺得文章對您有幫助，可以點選文章右下角【推薦】一下。您的鼓勵是作者堅持原創和持續寫作的最大動力！

博主一些其他平臺：
微信公眾號：寤言不寐
BiBili——小陳的學習記錄
Github——StevenEco
BiBili——記錄學習的小陳（計算機考研紀實）
掘金——小陳的學習記錄
知乎——小陳的學習記錄

聯絡方式

<a style="font-family: 微軟雅黑; font-size: 18px;" href="mailto:[email protected]">電子郵件：[email protected] </a>
<br/>
<br/>

社交媒體聯絡二維條碼：

【機器學習】數值分析03——任意曲線擬合