計算空間物體包圍球的兩種演演算法實現
1. 概述
在進行二維空間幾何運算的之前,往往會用包圍盒進行快速碰撞檢測,從而篩掉一些無法碰撞到的可能。而在三維中,比較常用的就是包圍球了。當然,如何計算包圍球是一個問題。
2. 詳論
2.1. naive演演算法
一個最簡單的思路就是,計算空間頂點在X、Y、Z方向上的最大值和最小值,那麼就可以得到8個頂點組成的包圍盒。取包圍球中心為包圍盒中心點,而包圍球半徑有的人認為可以取中心點到八個頂點的最大距離——這樣其實並不嚴密。最好還是計算中心點到所有頂點距離的最大值:
void BoundingSphere::GetBoundingSphereNative(const std::vector<Vec3d>& pointList)
{
if (pointList.empty())
{
return;
}
Vec3d minPoint(DBL_MAX, DBL_MAX, DBL_MAX);
Vec3d maxPoint(-DBL_MAX, -DBL_MAX, -DBL_MAX);
size_t vertexCount = pointList.size();
for (size_t vi = 0; vi < vertexCount; vi++)
{
if (minPoint.x() > pointList[vi].x())
{
minPoint.x() = pointList[vi].x();
}
if (minPoint.y() > pointList[vi].y())
{
minPoint.y() = pointList[vi].y();
}
if (minPoint.z() > pointList[vi].z())
{
minPoint.z() = pointList[vi].z();
}
if (maxPoint.x() < pointList[vi].x())
{
maxPoint.x() = pointList[vi].x();
}
if (maxPoint.y() < pointList[vi].y())
{
maxPoint.y() = pointList[vi].y();
}
if (maxPoint.z() < pointList[vi].z())
{
maxPoint.z() = pointList[vi].z();
}
}
Vec3d naiveCenter = (maxPoint + minPoint) / 2;
double naiveRadius = 0;
for (size_t vi = 0; vi < vertexCount; vi++)
{
naiveRadius = std::max(naiveRadius, (pointList[vi] - naiveCenter).length());
}
data = { naiveCenter.x(), naiveCenter.y(), naiveCenter.z(), naiveRadius };
}
這個演演算法的思路比較簡單,所以稱之為naive演演算法。
2.2. ritter演演算法
另外一種演演算法是一個名為ritter提出來的,所以稱為ritter演演算法。
首先計算出X方向上距離最遠的兩個點,Y方向上距離最遠的兩個點以及Z方向上距離最遠的兩個點。以這三個距離最遠的範圍作為初始直徑,這三個距離的中心點作為初始球心。
然後依次遍歷所有點,判斷點是否在這個包圍球內。如果不在,則更新包圍球。如下圖所示:
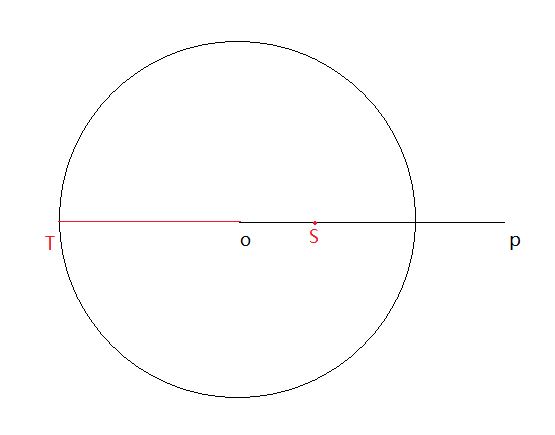
如果點P在我們的之前得到的包圍球之外,那麼延長點P與球心O的直線與球相較於T點,很顯然,新的直徑應該是點T與點P的一半:
令點T與點P的中心點為S,也就是新的球心位置。關鍵就是求向量\(\overrightarrow{OS}\),從而將球心O移動到新的球心S。
顯然,向量\(\overrightarrow{OS}\)的距離還是很好求的,只新的包圍球半徑與之前包圍球的半徑之差:
而向量\(\overrightarrow{OP}\)是已知的,根據向量關係,可求得:
最後將之前的球心O移動向量\(\overrightarrow{OS}\),就是新的包圍球的球心位置了。
具體的演演算法程式碼實現:
void BoundingSphere::GetBoundingSphereRitter(const std::vector<Vec3d>& pointList)
{
//
Vec3d minPoint(DBL_MAX, DBL_MAX, DBL_MAX);
Vec3d maxPoint(-DBL_MAX, -DBL_MAX, -DBL_MAX);
size_t minX = 0, minY = 0, minZ = 0;
size_t maxX = 0, maxY = 0, maxZ = 0;
size_t vertexCount = pointList.size();
for (size_t vi = 0; vi < vertexCount; vi++)
{
if (minPoint.x() > pointList[vi].x())
{
minPoint.x() = pointList[vi].x();
minX = vi;
}
if (minPoint.y() > pointList[vi].y())
{
minPoint.y() = pointList[vi].y();
minY = vi;
}
if (minPoint.z() > pointList[vi].z())
{
minPoint.z() = pointList[vi].z();
minZ = vi;
}
if (maxPoint.x() < pointList[vi].x())
{
maxPoint.x() = pointList[vi].x();
maxX = vi;
}
if (maxPoint.y() < pointList[vi].y())
{
maxPoint.y() = pointList[vi].y();
maxY = vi;
}
if (maxPoint.z() < pointList[vi].z())
{
maxPoint.z() = pointList[vi].z();
maxZ = vi;
}
}
//
double maxLength2 = (pointList[maxX] - pointList[minX]).length2();
Vec3d min = pointList[minX];
Vec3d max = pointList[maxX];
{
double yMaxLength2 = (pointList[maxY] - pointList[minY]).length2();
if (maxLength2 < yMaxLength2)
{
maxLength2 = yMaxLength2;
min = pointList[minY];
max = pointList[maxY];
}
double zMaxLength2 = (pointList[maxZ] - pointList[minZ]).length2();
if (maxLength2 < zMaxLength2)
{
maxLength2 = zMaxLength2;
min = pointList[minZ];
max = pointList[maxZ];
}
}
//
Vec3d ritterCenter = (min + max) / 2;
double ritterRadius = sqrt(maxLength2) / 2;
for (size_t i = 0; i < vertexCount; i++)
{
Vec3d d = pointList[i] - ritterCenter;
double dist2 = d.length2();
if (dist2 > ritterRadius * ritterRadius)
{
double dist = sqrt(dist2);
double newRadious = (dist + ritterRadius) * 0.5;
double k = (newRadious - ritterRadius) / dist;
ritterRadius = newRadious;
Vec3d temp = d * k;
ritterCenter = ritterCenter + temp;
}
}
data = { ritterCenter.x(), ritterCenter.y(), ritterCenter.z(), ritterRadius };
}
2.3. 其他
理論上來說,ritter演演算法的實現要優於naive演演算法,能夠得到更加貼合的包圍球。當然理論只是理論,具體的實現還要看最終的效果。根據文獻2中所說,經過Cesium的比對測試,19%的情況下,ritter演演算法的效果比naive演演算法差;11%的情況下,ritter演演算法的效果會比naive演演算法好。所以在Cesium中,包圍球的實現是把兩者都實現了一遍,然後取半徑較小的結果。