尋找領域不變數：從生成模型到因果表徵

1 領域不變的表徵

在遷移學習/領域自適應中，我們常常需要尋找領域不變的表徵(Domain-invariant Representation)^[1]，這種表示可被認為是學習到各領域之間的共性，並基於此共性進行遷移。而獲取這個表徵的過程就與深度學習中的「表徵學習」聯絡緊密^[2]。生成模型，自監督學習/對比學習和最近流行的因果表徵學習都可以視為獲取良好的領域不變表徵的工具。

2 生成模型的視角

生成模型的視角是在模型中引入隱變數(Latent Variable)，而學到的隱變數為資料提供了一個隱含表示(Latent Representation)。如下圖所示^[3]，生成模型描述了觀測到的資料\(\mathbf{x}\)由隱變數\(\mathbf{z}\)的一個生成過程：

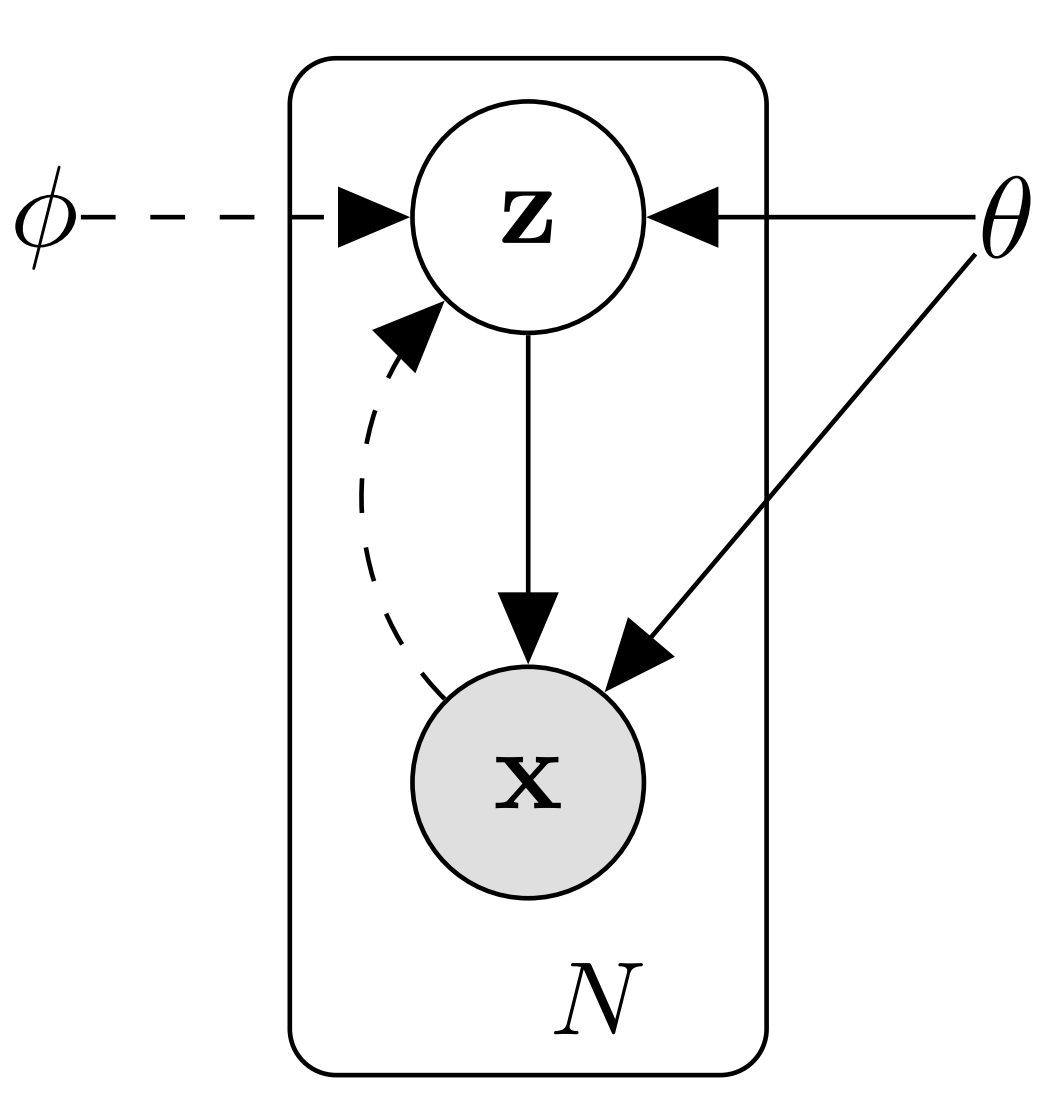
也即

\[p_{\boldsymbol{\theta}}(\mathbf{x})= \sum_{\mathbf{z}}p_{\boldsymbol{\theta}}(\mathbf{x}, \mathbf{\mathbf{z}})= \sum_{\mathbf{z}}p_{\boldsymbol{\theta}}(\mathbf{z})p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z}) \]

求和（或積分）項\(\sum_{\mathbf{z}}p_{\boldsymbol{\theta}}(\mathbf{z})p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})\)常常難以計算，而且\(\mathbf{z}\)的後驗分佈\(p_{\boldsymbol{\theta}}(\mathbf{z}|\mathbf{x})=p_{\boldsymbol{\theta}}(\mathbf{x} \mid \mathbf{z}) p_{\boldsymbol{\theta}}(\mathbf{z}) / p_{\boldsymbol{\theta}}(\mathbf{x})\)也難以推斷，導致EM演演算法不能使用。

VAE的思想是既然後驗\(p_{\boldsymbol{\theta}}(\mathbf{z} \mid \mathbf{x})\)難以進行推斷，那我們可以採用其變分近似後驗分佈\(q_\phi(\mathbf{z} \mid \mathbf{x})\)（對應重引數化後的編碼器），而資料的生成過程\(p_{\boldsymbol{\theta}}(\mathbf{x} \mid \mathbf{z})\)則視為解碼器。如下圖所示。

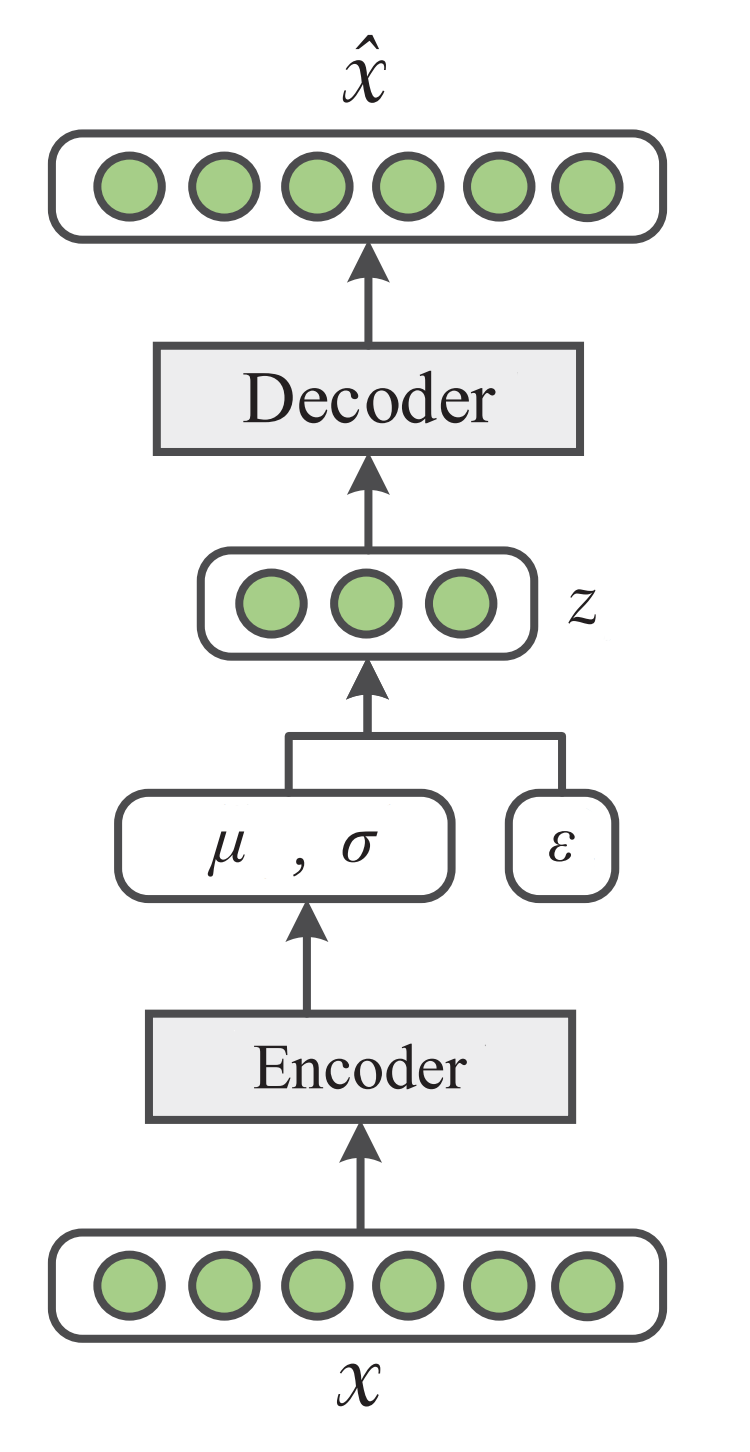
變分自編碼器的優化目標為最大化與資料點\(x\)相關聯的變分下界：

\[\begin{aligned} \widetilde{\mathcal{L}}_{\mathrm{VAE}}(\mathbf{x} ; \theta, \phi) &=-D_{K L}\left(q_\phi(\mathbf{z} \mid \mathbf{x}) \| p_\theta(\mathbf{z})\right)+ \mathbb{E}_{\mathbf{z}\sim q_{\phi}(\mathbf{z}|\mathbf{x})} \log p_\theta(\mathbf{x} \mid \mathbf{z}) \\ & \leqslant \log p_{\boldsymbol{ \theta}}(\mathbf{x}) \end{aligned} \]

上面的第一項使近似後驗分佈\(q(\mathbf{z}|\mathbf{x})\)和模型先驗\(p_{\boldsymbol{\theta}}(\mathbf{z})\)（一般設為高斯）儘可能接近（這樣的目的是使解碼器的輸入儘可能服從高斯分佈，從而使解碼器對隨機輸入也有很好的輸出）；第二項即為解碼器的重構對數似然。

接下來我們說一下如何從近似後驗分佈\(q(\mathbf{z}|\mathbf{x})\)中取樣獲得\(\mathbf{z}\)，因為這\(\mathbf{z}\)不是由一個函數產生，而是由一個隨機取樣過程產生（它的輸出會隨我們每次查詢而發生變化），故直接用一個神經網路表示\(\mathbf{z} = g(\mathbf{x})\)是不行的，這裡我們需要用到一個重引數化技巧(reparametrization trick)：

\[\begin{aligned} & \mathbf{z} = g_{\phi}(\epsilon, \mathbf{x})=\mathbf{\mu} + \mathbf{\sigma}\odot\mathbf{\epsilon} \\ & \mathbf{\mu},\mathbf{\sigma} = \text{Encoder}_{\phi}(x)\\ & \mathbf{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \end{aligned} \]

這樣我們即能保證\(\mathbf{z}\)來自隨機取樣的要求，也能通過反向傳播進行訓練了。

這裡提一下條件變分自編碼器^[4]，它在變分自編碼器的基礎上增加了條件資訊\(\mathbf{c}\)（比如資料\(\mathbf{x}\)的標籤資訊），如下圖所示

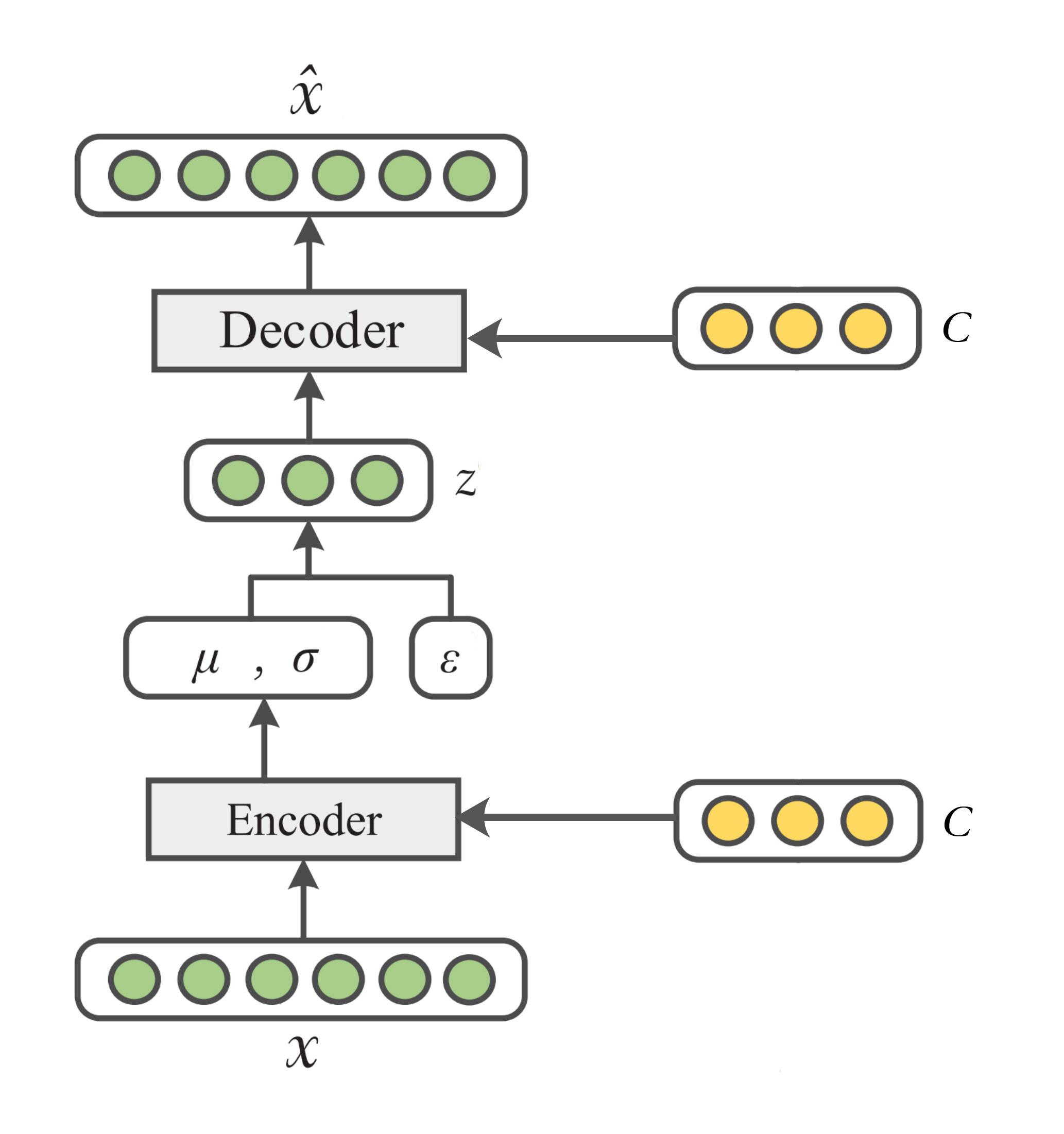
變分自編碼器所要最大化的函數可以表示為：

\[\begin{aligned} \widetilde{\mathcal{L}}_{\mathrm{CVAE}}(\mathbf{x}, \mathbf{c} ; \theta, \phi) &=-D_{K L}\left(q_\phi(\mathbf{z} \mid \mathbf{x}, \mathbf{c}) \| p_\theta(\mathbf{z} \mid \mathbf{c})\right)+\mathbb{E}_{\mathbf{z}\sim q_{\phi}(\mathbf{z}|\mathbf{x}, \mathbf{c})}\log p_\theta(\mathbf{x} \mid \mathbf{z}, \mathbf{c})\\ & \leqslant \log p_{\boldsymbol{ \theta}}(\mathbf{x|\mathbf{c}}) \end{aligned} \]

關於自編碼器和變分自編碼在MNIST資料集上的程式碼實現可以參照GitHub專案^[5]。

訓練完成後，VAE的隱向量\(\mathbf{z}\sim q_{\phi}(\mathbf{z}|\mathbf{x})\)和CVAE的隱向量\(\mathbf{z}\sim q_{\phi}(\mathbf{z}|\mathbf{x}, \mathbf{c})\)的對比如下：

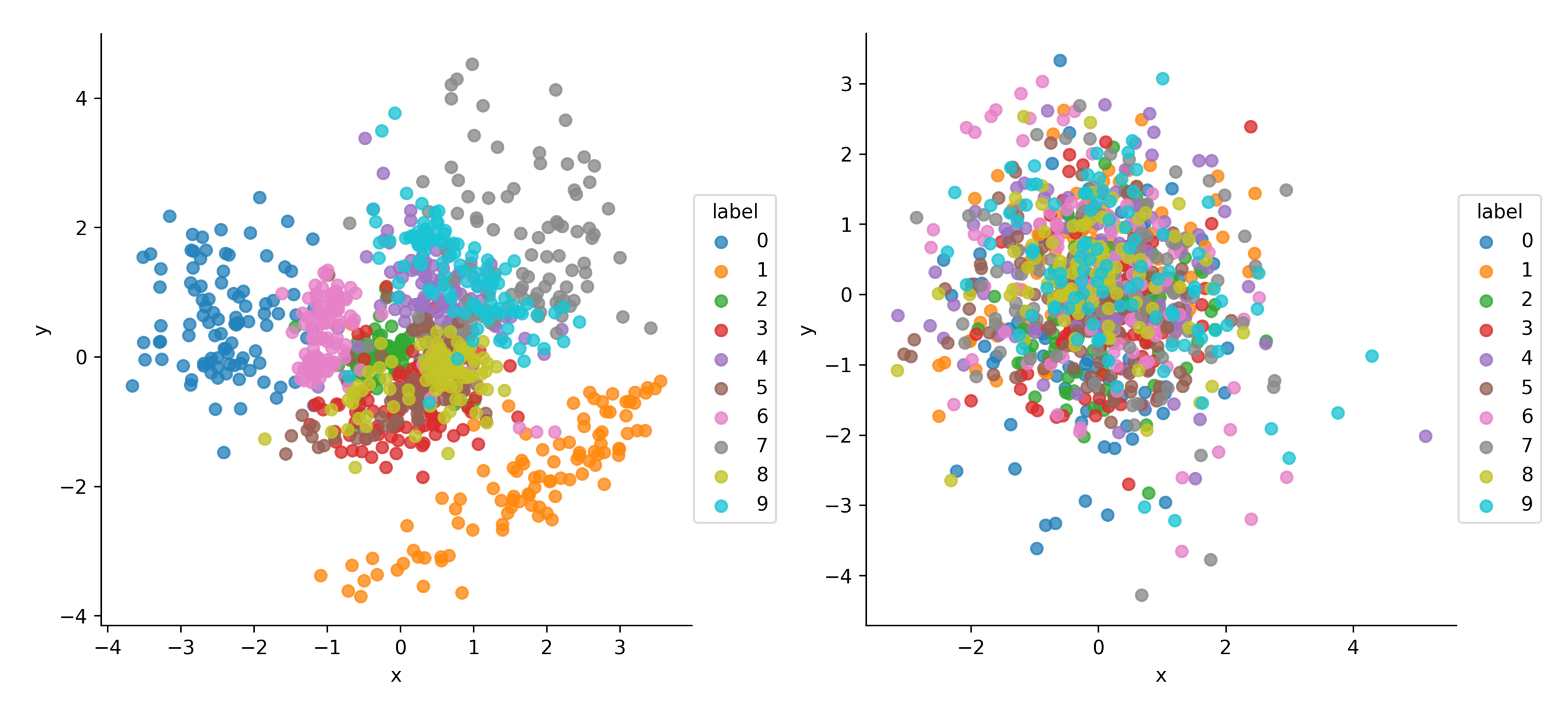
可以看到CVAE的隱空間相比VAE的隱空間並沒有編碼標籤資訊，而是去編碼其它的關於資料\(\mathbf{x}\)的分佈資訊，可視為一種解耦表徵學習（disentangled representation learning）技術。

就我們的遷移學習/領域自適應任務而言，訓練生成模型獲得了隱向量之後就已經完成目標，之後可以將隱向量拿到其它領域的任務中去用了。不過有時訓練生成模型的最終目的還是為了生成原始資料。接下來我們來對比兩者的影象生成效果。移除編碼器部分，隨機取樣\(\mathbf{z}\)，VAE的生成\(p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})\)和CVAE的生成\(p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z}, \mathbf{c})\)如下圖所示，其中CVAE會將影象的標籤資訊\(\mathbf{c}\)做為解碼器的輸入。

可以看到其中所編碼的標籤資訊發揮的重要作用。

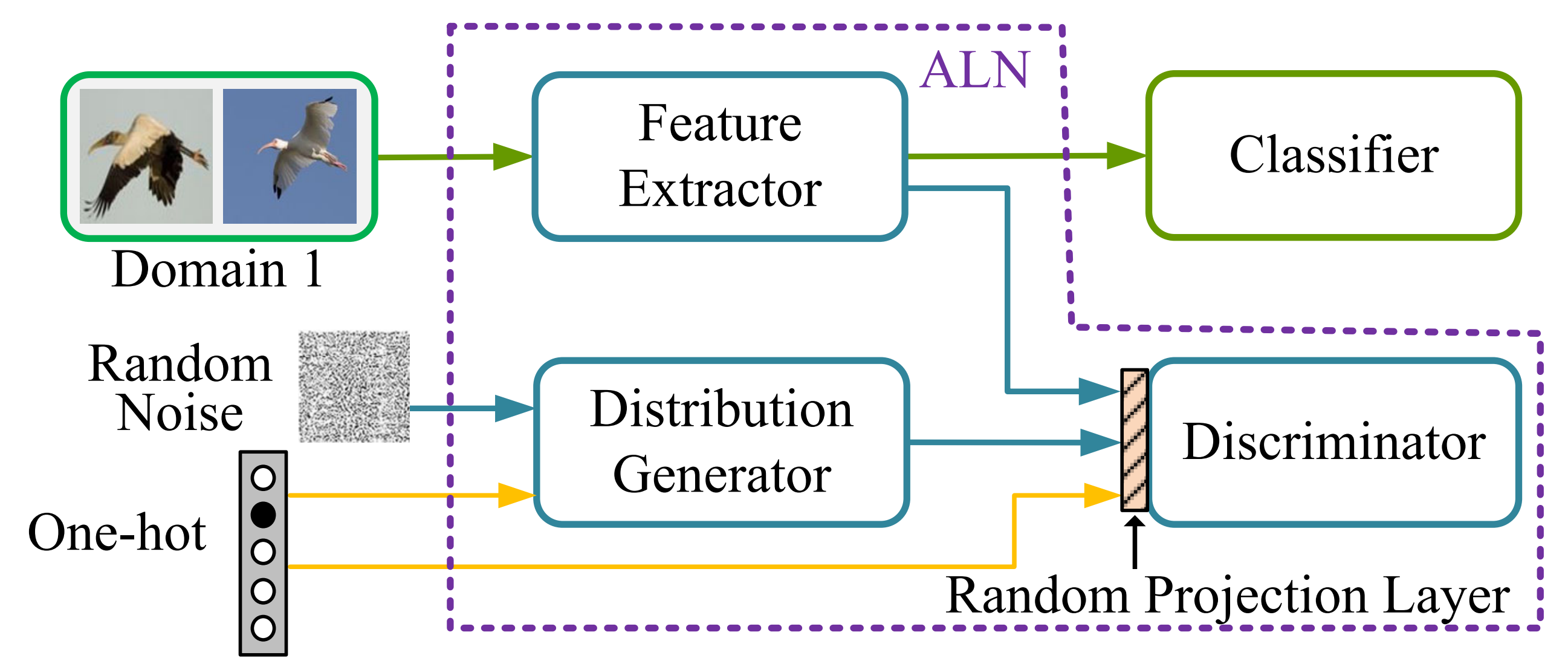
這裡補充一下，提取領域不變的表示也可以通過簡單的特徵提取器+GAN對抗訓練機制來得到。如在論文^[6]中，設定了一個生成器根據隨機噪聲和標籤編碼來生成「偽」特徵，並訓練判別器來區分特徵提取器得到的特徵和「偽」特徵。此外，作者還採用了隨機投影層來使得判別器更難區分這兩種特徵，使得對抗網路更穩定。其架構如下圖所示：

2 自監督學習/對比學習的視角

在自監督預訓練中，其實也可以看做是在學習\(p(\mathbf{x})\)的結構，我們要求該過程能夠學習出一些對建模\(p(\mathbf{y}|\mathbf{x})\)（對應下游的分類任務）同樣有用的特徵（潛在因素）。因為如果\(\mathbf{y}\)與\(\mathbf{x}\)的成因之一非常相關，那麼\(p(\mathbf{x})\)和\(p(\mathbf{y}|\mathbf{x})\)也會緊密關聯，故試圖找到變化潛在因素的自監督表示學習會非常有用。自然語言處理中的經典模型BERT^[7]便是基於自監督學習的思想。

而對比學習也可以視為自監督學習的一種，它是通過構造錨點樣本、正樣本和負樣本之間的關係來學習表徵。對於任意錨點樣本\(\mathbf{x}\)，我們用\(\mathbf{x}^+\)和\(\mathbf{x}^-\)分別表示其正樣本和負樣本，然後\(f(\cdot)\)表示要訓練的特徵提取器。此時，學習目標為限制錨點樣本與負樣本之間的距離遠大於其與正樣本之間的距離（此處的距離為在表徵空間的距離），即：

\[d(f(\mathbf{x}), f(\mathbf{x}^+)) \geq d(f(\mathbf{x}), f(\mathbf{x}^-)) \]

其中，\(d(\cdot, \cdot)\)為一可客製化的距離度量函數，常用的是如下的餘弦相似度：

\[\operatorname{cos\_sim}(\mathbf{a}, \mathbf{b})=\frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\|\|\mathbf{b}\|} \]

當向量\(\mathbf{a}\)、\(\mathbf{b}\)歸一化後，餘弦相似度等價於向量內積。此外，互資訊也可以作為相似度的度量。

在經典的SimCLR^[8]架構按照如下圖所示的影象增強（比如旋轉裁剪等）方式產生正樣本：

如上圖所示，它對每張輸入的圖片進行兩次亂資料增強(如旋轉剪裁等)來得到\(\mathbf{x}_i\)和\(\mathbf{x}_j\)。對於\(\mathbf{x_i}\)而言，\(\mathbf{x}_j\)為其配對的正樣本，而其它\(N-1\)個樣本則視為負樣本。

對比學習損失函數InfoNCE如下所示：

\[L_{infoN C E}=-\mathbb{E}_{\mathbf{x}\sim \hat{p}_{data}}\left[ \log \frac{\exp \left(\operatorname{sim}\left(f(\mathbf{x}), f(\mathbf{x}^+)\right) / \tau\right)}{\exp \left(\operatorname{sim}\left(f(\mathbf{x}), f(\mathbf{x}^+)\right) / \tau\right)+\sum_{j=1}^{N-1} \exp \left(\operatorname{sim}\left(f(\mathbf{x}),f(\mathbf{x}_j)\right) / \tau\right)}\right] \]

這裡\(\mathbf{x}_j\)表示第\(j\)個負樣本。

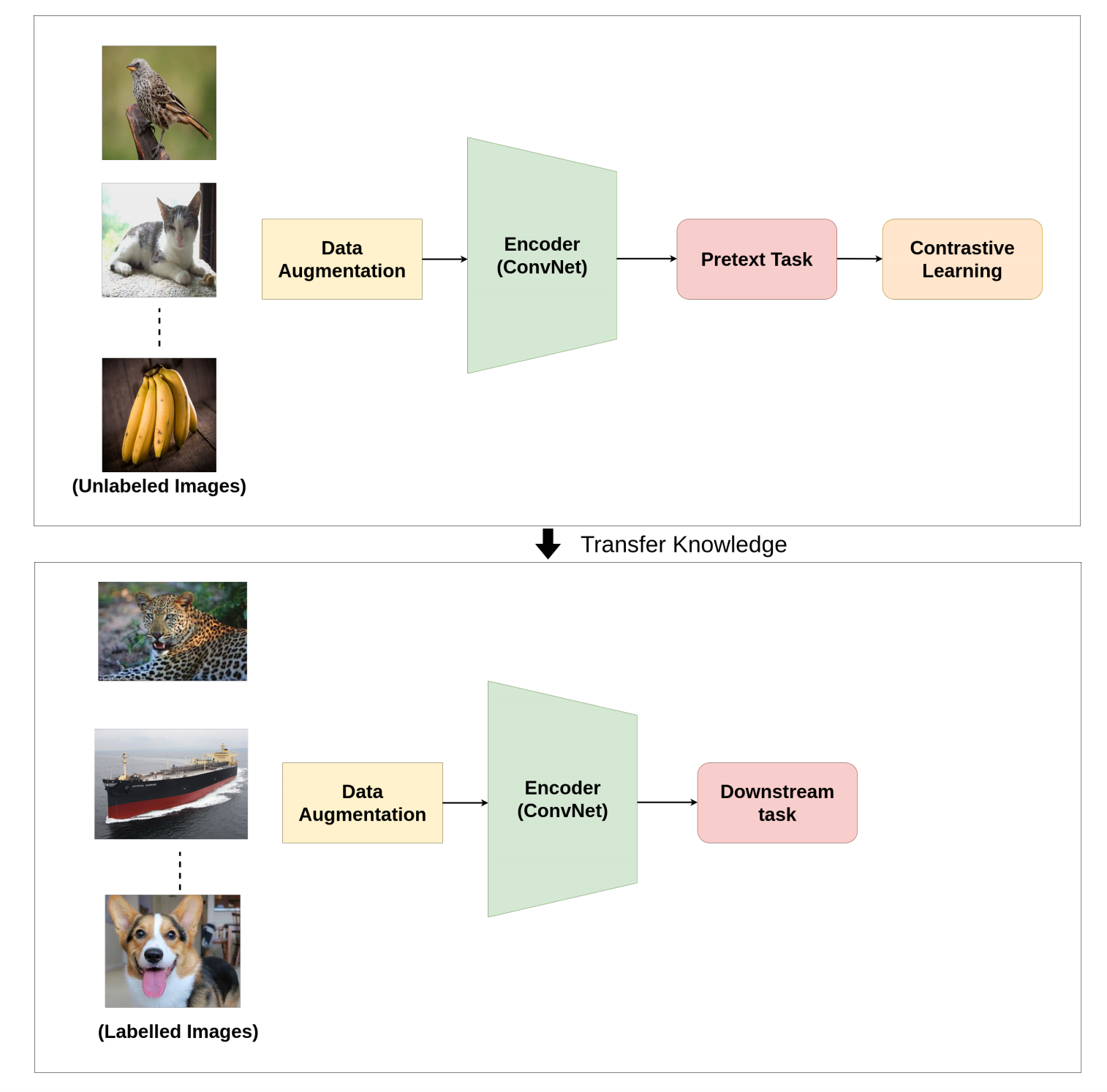
對比學習一般也是用來獲取embeddings，然後用於下游的有監督任務中，如下圖所示^[9]：

3 因果推斷的視角

前面我們提到在對比學習中可以運用資料增強來捕捉域不變特徵，然而這種資料增強的框架也可以從因果表徵學習的視角來看。因果推斷中的因果不變數同樣也可以對應到領域不變的表徵。

如今年CVPR 22的一篇論文^[10]所述，原始資料\(X\)由因果因子\(S\)（如影象本身的語意）和非因果因子\(U\)(如影象的風格)混合決定，且只有\(S\)能夠影響原始資料的類別標籤。注意，我們不能直接將原始資料量化為\(X=f(S, U)\)，因為因果因子/非因果因子一般不能觀測到並且不能被形式化。

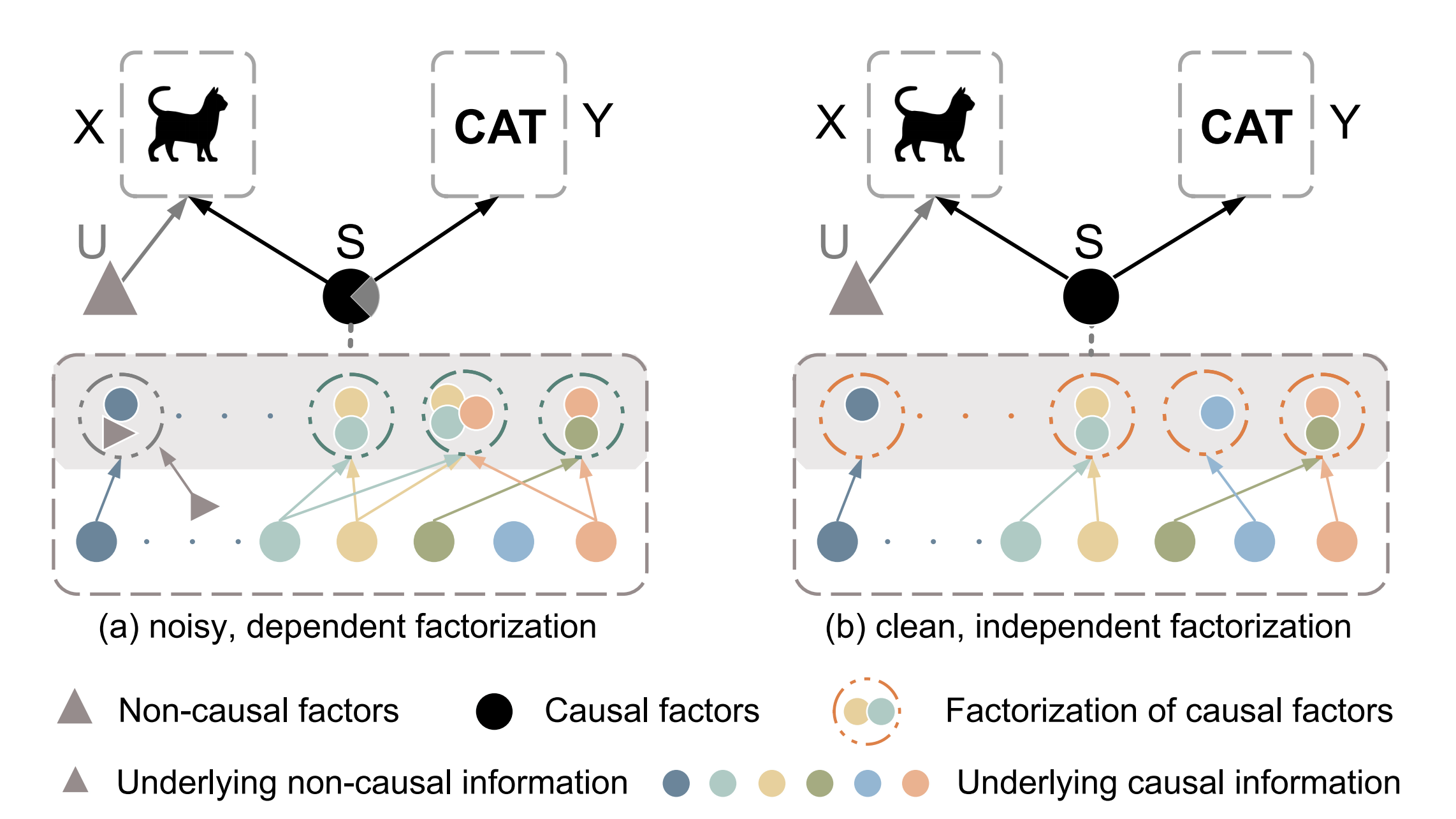
這裡的任務為將因果因子\(S\)從原始資料中提取出來，而這可以在因果乾預\(P(Y\mid do(U), S)\)的幫助下完成，具體的措施類似於我們前面所說的影象增強，如下圖所示：

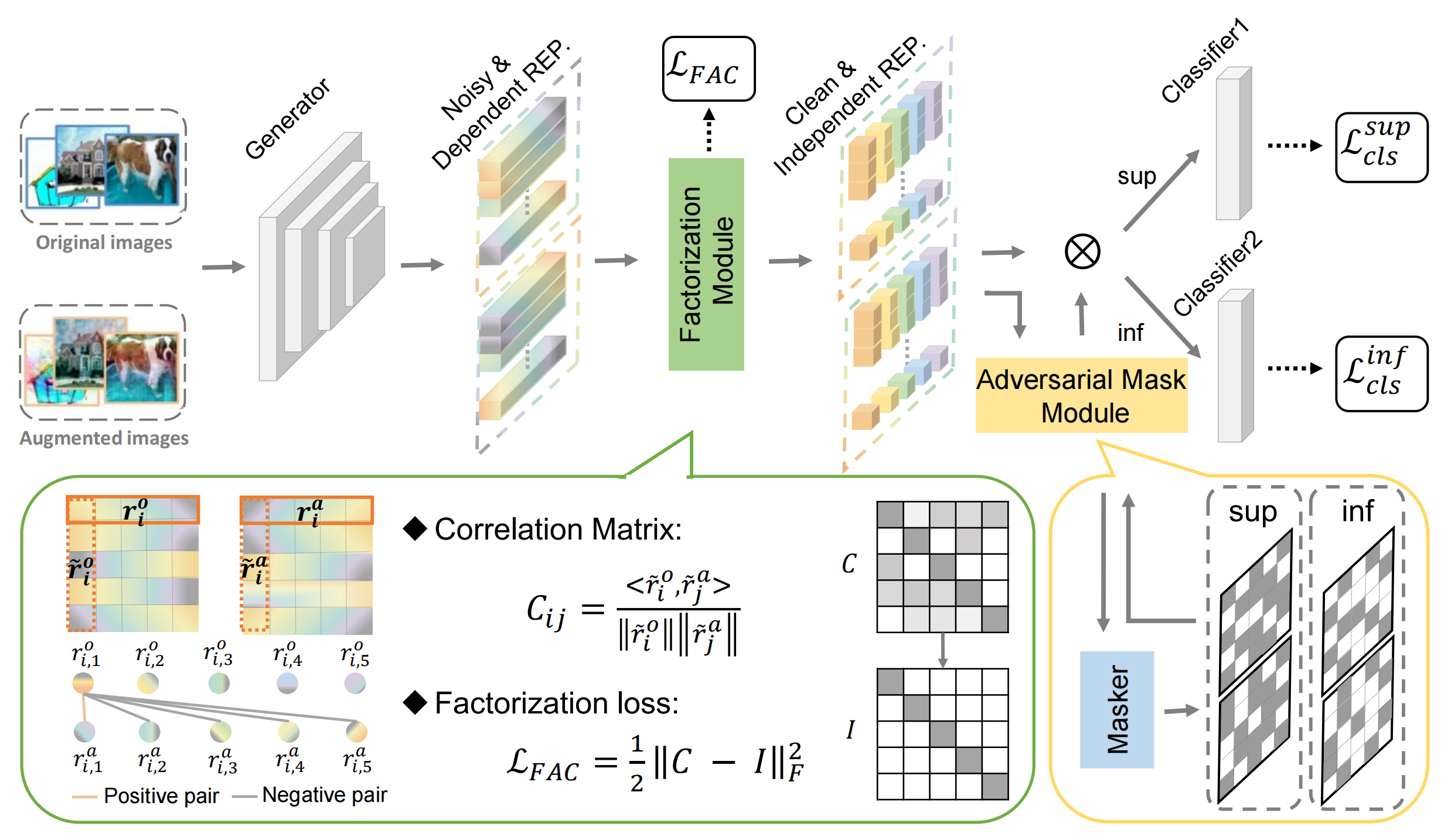
如圖，論文對非因果因子採用因果介入來生成增強後的影象，然後將原始和增強影象的表徵送到因子分解模組，該模組使用分解損失函數來迫使影象表徵和非因果因子分離。最後，通過對抗掩碼模組讓生成器和掩碼器之間形成對抗，使得表徵更適用於之後的分類任務。

參考

[1] 王晉東，陳益強. 遷移學習導論（第2版）[M]. 電子工業出版社, 2022.
[2] Goodfellow I, Bengio Y, Courville A. Deep learning[M]. MIT press, 2016.
[3] Kingma D P, Welling M. Auto-encoding variational bayes[C]. ICLR, 2014.
[4] Sohn K, Lee H, Yan X. Learning structured output representation using deep conditional generative models[J]. Advances in neural information processing systems, 2015, 28.
[5] https://github.com/timbmg/VAE-CVAE-MNIST
[6] Zhang L, Lei X, Shi Y, et al. Federated learning with domain generalization[J]. arXiv preprint arXiv:2111.10487, 2021.
[7] Devlin J, Chang M W, Lee K, et al. Bert: Pre-training of deep bidirectional transformers for language understanding[J]. NAACL, 2018.
[8] Chen T, Kornblith S, Norouzi M, et al. A simple framework for contrastive learning of visual representations[C]//International conference on machine learning. PMLR, 2020: 1597-1607.
[9] Jaiswal A, Babu A R, Zadeh M Z, et al. A survey on contrastive self-supervised learning[J]. Technologies, 2020, 9(1): 2.
[10] Lv F, Liang J, Li S, et al. Causality Inspired Representation Learning for Domain Generalization[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022: 8046-8056.