跟我學Python影象處理丨帶你掌握傅立葉變換原理及實現

摘要：傅立葉變換主要是將時間域上的訊號轉變為頻率域上的訊號，用來進行影象除噪、影象增強等處理。

本文分享自華為雲社群《[Python影象處理] 二十二.Python影象傅立葉變換原理及實現》，作者：eastmount。

本文主要講解影象傅立葉變換的相關內容，在數位影像處理中，有兩個經典的變換被廣泛應用——傅立葉變換和霍夫變換。其中，傅立葉變換主要是將時間域上的訊號轉變為頻率域上的訊號，用來進行影象除噪、影象增強等處理。

影象傅立葉變換原理

傅立葉變換（Fourier Transform，簡稱FT）常用於數位訊號處理，它的目的是將時間域上的訊號轉變為頻率域上的訊號。隨著域的不同，對同一個事物的瞭解角度也隨之改變，因此在時域中某些不好處理的地方，在頻域就可以較為簡單的處理。同時，可以從頻域裡發現一些原先不易察覺的特徵。傅立葉定理指出「任何連續週期訊號都可以表示成（或者無限逼近）一系列正弦訊號的疊加。」

下面參照李老師「Python+OpenCV影象處理」中的一個案例，非常推薦同學們去學習。如下圖所示，他將某飲料的製作過程的時域角度轉換為頻域角度。

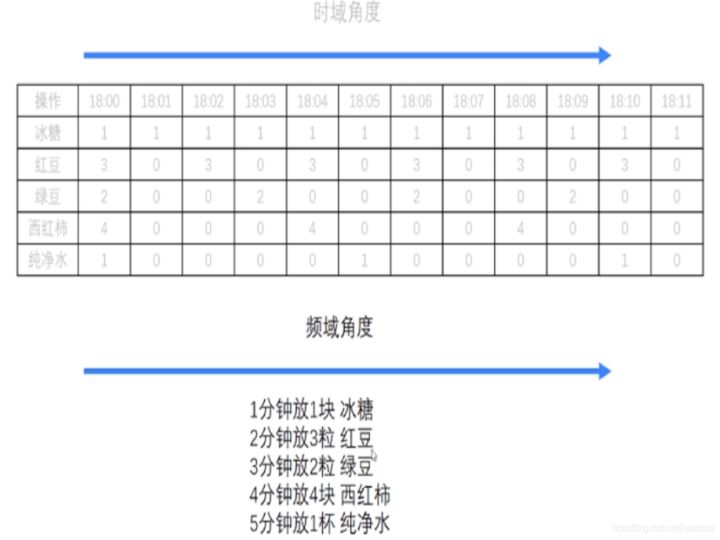
繪製對應的時間圖和頻率圖如下所示：

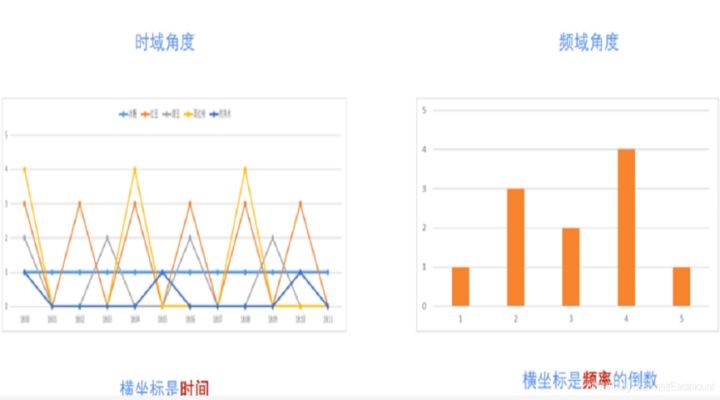
傅立葉公式如下，其中w表示頻率，t表示時間，為複變函數。它將時間域的函數表示為頻率域的函數f(t)的積分。

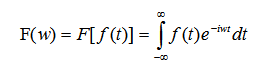
傅立葉變換認為一個周期函數（訊號）包含多個頻率分量，任意函數（訊號）f(t)可通過多個周期函數（或基函數）相加合成。從物理角度理解，傅立葉變換是以一組特殊的函數（三角函數）為正交基，對原函數進行線性變換，物理意義便是原函數在各組基函數的投影。如下圖所示，它是由三條正弦曲線組合成。

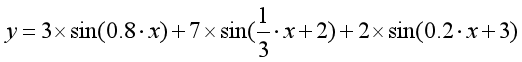
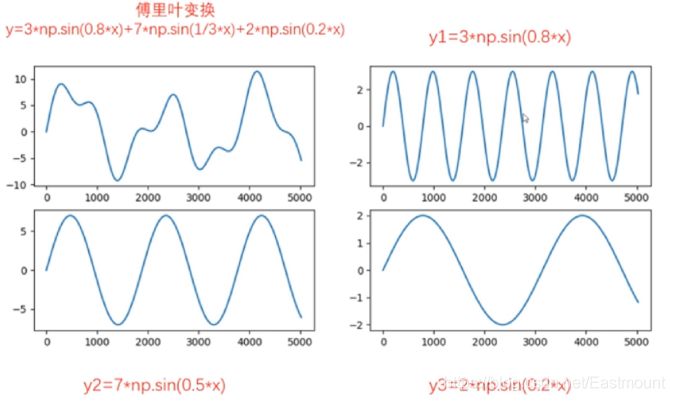
傅立葉變換可以應用於影象處理中，經過對影象進行變換得到其頻譜圖。從譜頻圖裡頻率高低來表徵影象中灰度變化劇烈程度。影象中的邊緣訊號和噪聲訊號往往是高頻訊號，而影象變化頻繁的影象輪廓及背景等訊號往往是低頻訊號。這時可以有針對性的對影象進行相關操作，例如影象除噪、影象增強和銳化等。

二維影象的傅立葉變換可以用以下數學公式（15-3）表達，其中f是空間域（Spatial Domain）)值，F是頻域（Frequency Domain）值

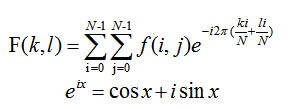
對上面的傅立葉變換有了大致的瞭解之後，下面通過Numpy和OpenCV分別講解影象傅立葉變換的演演算法及操作程式碼。

二.Numpy實現傅立葉變換

Numpy中的 FFT包提供了函數 np.fft.fft2()可以對訊號進行快速傅立葉變換，其函數原型如下所示，該輸出結果是一個複數陣列（Complex Ndarry）。

fft2(a, s=None, axes=(-2, -1), norm=None)

• a表示輸入影象，陣列狀的複雜陣列
• s表示整數序列，可以決定輸出陣列的大小。輸出可選形狀（每個轉換軸的長度），其中s[0]表示軸0，s[1]表示軸1。對應fit(x,n)函數中的n，沿著每個軸，如果給定的形狀小於輸入形狀，則將剪下輸入。如果大於則輸入將用零填充。如果未給定’s’，則使用沿’axles’指定的軸的輸入形狀
• axes表示整數序列，用於計算FFT的可選軸。如果未給出，則使用最後兩個軸。「axes」中的重複索引表示對該軸執行多次轉換，一個元素序列意味著執行一維FFT
• norm包括None和ortho兩個選項，規範化模式（請參見numpy.fft）。預設值為無

Numpy中的fft模組有很多函數，相關函數如下：

#計算一維傅立葉變換
numpy.fft.fft(a, n=None, axis=-1, norm=None)
#計算二維的傅立葉變換
numpy.fft.fft2(a, n=None, axis=-1, norm=None)
#計算n維的傅立葉變換
numpy.fft.fftn()
#計算n維實數的傅立葉變換
numpy.fft.rfftn()
#返回傅立葉變換的取樣頻率
numpy.fft.fftfreq()
#將FFT輸出中的直流分量移動到頻譜中央
numpy.fft.shift()

下面的程式碼是通過Numpy庫實現傅立葉變換，呼叫np.fft.fft2()快速傅立葉變換得到頻率分佈，接著呼叫np.fft.fftshift()函數將中心位置轉移至中間，最終通過Matplotlib顯示效果圖。

# -*- coding: utf-8 -*-
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
#讀取影象
img = cv.imread('test.png', 0)
#快速傅立葉變換演演算法得到頻率分佈
f = np.fft.fft2(img)
#預設結果中心點位置是在左上角,
#呼叫fftshift()函數轉移到中間位置
fshift = np.fft.fftshift(f) 
#fft結果是複數, 其絕對值結果是振幅
fimg = np.log(np.abs(fshift))
#展示結果
plt.subplot(121), plt.imshow(img, 'gray'), plt.title('Original Fourier')
plt.axis('off')
plt.subplot(122), plt.imshow(fimg, 'gray'), plt.title('Fourier Fourier')
plt.axis('off')
plt.show()

輸出結果如圖15-2所示，左邊為原始影象，右邊為頻率分佈圖譜，其中越靠近中心位置頻率越低，越亮（灰度值越高）的位置代表該頻率的訊號振幅越大。

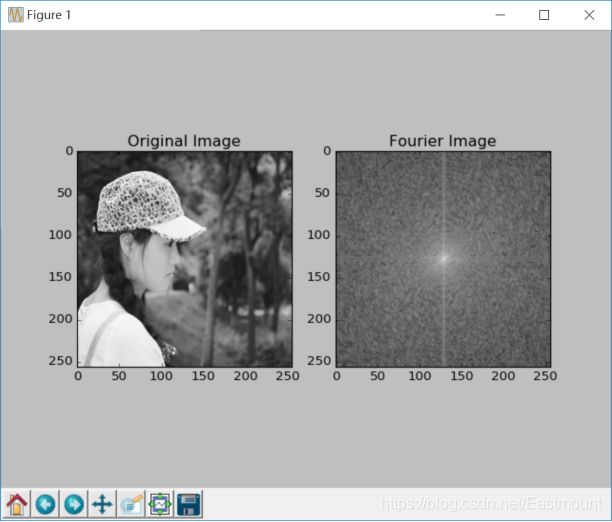
三.Numpy實現傅立葉逆變換

下面介紹Numpy實現傅立葉逆變換，它是傅立葉變換的逆操作，將頻譜影象轉換為原始影象的過程。通過傅立葉變換將轉換為頻譜圖，並對高頻（邊界）和低頻（細節）部分進行處理，接著需要通過傅立葉逆變換恢復為原始效果圖。頻域上對影象的處理會反映在逆變換影象上，從而更好地進行影象處理。

影象傅立葉變化主要使用的函數如下所示：

#實現影象逆傅立葉變換，返回一個複數陣列
numpy.fft.ifft2(a, n=None, axis=-1, norm=None)
#fftshit()函數的逆函數，它將頻譜影象的中心低頻部分移動至左上角
numpy.fft.fftshift()
#將複數轉換為0至255範圍
iimg = numpy.abs(逆傅立葉變換結果)

下面的程式碼分別實現了傅立葉變換和傅立葉逆變換。

# -*- coding: utf-8 -*-
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
#讀取影象
img = cv.imread('Lena.png', 0)
#傅立葉變換
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
res = np.log(np.abs(fshift))
#傅立葉逆變換
ishift = np.fft.ifftshift(fshift)
iimg = np.fft.ifft2(ishift)
iimg = np.abs(iimg)
#展示結果
plt.subplot(131), plt.imshow(img, 'gray'), plt.title('Original Image')
plt.axis('off')
plt.subplot(132), plt.imshow(res, 'gray'), plt.title('Fourier Image')
plt.axis('off')
plt.subplot(133), plt.imshow(iimg, 'gray'), plt.title('Inverse Fourier Image')
plt.axis('off')
plt.show()

輸出結果如圖15-4所示，從左至右分別為原始影象、頻譜影象、逆傅立葉變換轉換影象。

四.OpenCV實現傅立葉變換

OpenCV 中相應的函數是cv2.dft()和用Numpy輸出的結果一樣，但是是雙連結的。第一個通道是結果的實數部分，第二個通道是結果的虛數部分，並且輸入影象要首先轉換成 np.float32 格式。其函數原型如下所示：

dst = cv2.dft(src, dst=None, flags=None, nonzeroRows=None)

• src表示輸入影象，需要通過np.float32轉換格式
• dst表示輸出影象，包括輸出大小和尺寸
• flags表示轉換標記，其中DFT _INVERSE執行反向一維或二維轉換，而不是預設的正向轉換；DFT _SCALE表示縮放結果，由陣列元素的數量除以它；DFT _ROWS執行正向或反向變換輸入矩陣的每個單獨的行，該標誌可以同時轉換多個向量，並可用於減少開銷以執行3D和更高維度的轉換等；DFT _COMPLEX_OUTPUT執行1D或2D實陣列的正向轉換，這是最快的選擇，預設功能；DFT _REAL_OUTPUT執行一維或二維複數陣列的逆變換，結果通常是相同大小的複數陣列，但如果輸入陣列具有共軛複數對稱性，則輸出為真實陣列
• nonzeroRows表示當引數不為零時，函數假定只有nonzeroRows輸入陣列的第一行（未設定）或者只有輸出陣列的第一個（設定）包含非零，因此函數可以處理其餘的行更有效率，並節省一些時間；這種技術對計算陣列互相關或使用DFT折積非常有用

注意，由於輸出的頻譜結果是一個複數，需要呼叫cv2.magnitude()函數將傅立葉變換的雙連結結果轉換為0到255的範圍。其函數原型如下：

cv2.magnitude(x, y)

• x表示浮點型X座標值，即實部
• y表示浮點型Y座標值，即虛部
  最終輸出結果為幅值，即：

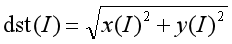
完整程式碼如下所示：

# -*- coding: utf-8 -*-
import numpy as np
import cv2
from matplotlib import pyplot as plt
#讀取影象
img = cv2.imread('Lena.png', 0)
#傅立葉變換
dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)
#將頻譜低頻從左上角移動至中心位置
dft_shift = np.fft.fftshift(dft)
#頻譜影象雙連結複數轉換為0-255區間
result = 20*np.log(cv2.magnitude(dft_shift[:,:,0], dft_shift[:,:,1]))
#顯示影象
plt.subplot(121), plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(result, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

輸出結果如圖15-5所示，左邊為原始「Lena」圖，右邊為轉換後的頻譜影象，並且保證低頻位於中心位置。

五.OpenCV實現傅立葉逆變換

在OpenCV 中，通過函數cv2.idft()實現傅立葉逆變換，其返回結果取決於原始影象的型別和大小，原始影象可以為實數或複數。其函數原型如下所示：

dst = cv2.idft(src[, dst[, flags[, nonzeroRows]]])

• src表示輸入影象，包括實數或複數
• dst表示輸出影象
• flags表示轉換標記
• nonzeroRows表示要處理的dst行數，其餘行的內容未定義（請參閱dft描述中的折積範例）

完整程式碼如下所示：

# -*- coding: utf-8 -*-
import numpy as np
import cv2
from matplotlib import pyplot as plt
#讀取影象
img = cv2.imread('Lena.png', 0)
#傅立葉變換
dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)
dftshift = np.fft.fftshift(dft)
res1= 20*np.log(cv2.magnitude(dftshift[:,:,0], dftshift[:,:,1]))
#傅立葉逆變換
ishift = np.fft.ifftshift(dftshift)
iimg = cv2.idft(ishift)
res2 = cv2.magnitude(iimg[:,:,0], iimg[:,:,1])
#顯示影象
plt.subplot(131), plt.imshow(img, 'gray'), plt.title('Original Image')
plt.axis('off')
plt.subplot(132), plt.imshow(res1, 'gray'), plt.title('Fourier Image')
plt.axis('off')
plt.subplot(133), plt.imshow(res2, 'gray'), plt.title('Inverse Fourier Image')
plt.axis('off')
plt.show()

輸出結果如圖15-6所示，第一幅圖為原始「Lena」圖，第二幅圖為傅立葉變換後的頻譜影象，第三幅圖為傅立葉逆變換，頻譜影象轉換為原始影象的過程。

六.總結

傅立葉變換的目的並不是為了觀察影象的頻率分佈（至少不是最終目的），更多情況下是為了對頻率進行過濾，通過修改頻率以達到影象增強、影象去噪、邊緣檢測、特徵提取、壓縮加密等目的。下一篇文章，作者將結合傅立葉變換和傅立葉逆變換講解它的應用。

點選關注，第一時間瞭解華為雲新鮮技術~