javascript怎麼求素數 - tw511教學網

求素數的方法：1、遍歷1~n區間中的所有自然數給n來除，若餘數為0則表示該數n不是素數，否則就是素數，語法「for(i=2;i<n;i++){if(n%i===0){return false;}}」。2、利用素數平方根範圍，語法「for(i=2;i<=Math.sqrt(n);i++){if(n%i===0){return false;}}」。

前端（vue）入門到精通課程：進入學習

本教學操作環境：windows7系統、javascript1.8.5版、Dell G3電腦。

素數的概念

素數又叫質數，素數是指在大於1的自然數中，除了1和它本身以外，不能被其他自然數整除的數。

100以內的素數：2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97，共計25個。

JavaScript判定素數的四種方法

1、素數只能被1和自身整除

素數只能被1和自身整除，所以遍歷（1，n）開區間中的所有自然數給n來除，若存在整除，即餘數為0，則表示該數n不是素數，否則就是素數。

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  for (let i = 2; i < n; i++) {
    if (n % i === 0) {
      return false;
    }
  }
  return true;
}

但是這種演演算法的複雜度為O(n)

2、素數平方根範圍

假設n不是素數，則n除了可以被1和n整除外，還可以被i、j整除，即 n / i = j...0，比如15不是素數，15 / 3 = 5，比如35不是素數，35 / 5 = 7，此時i,j必然分別處於(1, Math.sqrt(n)]和[Math.sqrt(n), n）之中，比如Math.sqrt(15) ≈ 3.8，則 3處於（1，3.8]，5處於[3.8, 15）。比如Math.sqrt(4) = 2，則2處於(1,2]中，也處於[2,4)中。

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  for (let i = 2; i <= Math.sqrt(n); i++) {
    if (n % i === 0) {
      return false;
    }
  }
  return true;
}

此時演演算法複雜度為O（sqrt(n)）

3、素數不能非2的其他偶數

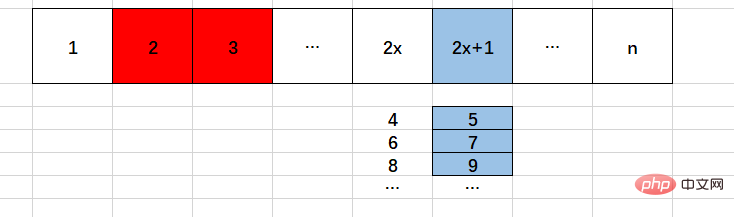
除了2，所有偶數都不是素數

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  if (n % 2 === 0) {
    return false;
  }
 
  for (let i = 3; i <= Math.sqrt(n); i += 2) {
    if (n % i === 0) {
      return false;
    }
  }
  return true;
}

for迴圈中n，只能為上圖淺藍色部分。

因此上面演演算法減少了一半的迴圈，時間複雜度為O（sqrt(n) / 2）

需要注意的是，本演演算法的程式碼不能將n % 2 === 0 的判斷條件加入到迴圈中，如下程式碼存在漏洞

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  for (let i = 3; i <= Math.sqrt(n); i += 2) {
    if (n % 2 === 0 || n % i === 0) {
      return false;
    }
  }
  return true;
}

此時4、6、8都會被判定為素數。

漏洞形成的原因是，for迴圈的迴圈條件 i <= Math.sqrt(n) 不成立，比如n=4時，i <= Math.sqrt(4) 不成立，導致n無法進入迴圈中n % 2 === 0 的判斷，而是直接退出迴圈，return true。

該演演算法只能保證迴圈條件 i <= Math.sqrt(n) 成立的n值判斷素數正確，即 n >= i^2 = 9 時。

4、大於等於5的素數一定和6的倍數相鄰

大於等於5的素數一定和6的倍數相鄰

（注意這句話不等價於：和6的倍數相鄰的數一定是大於5的素數，該結論不成立。）

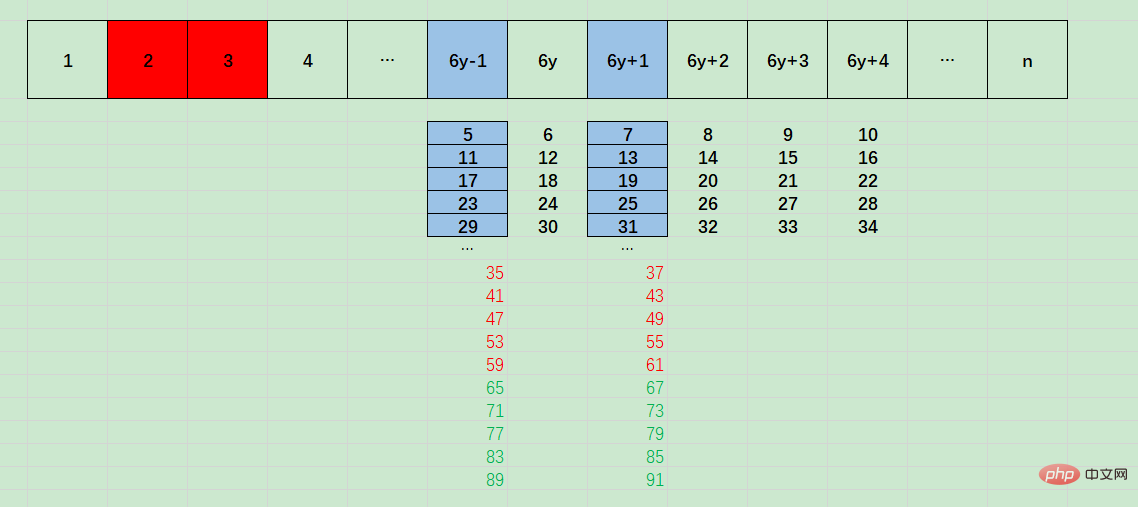
如上圖中，將大於等於5的數分為了：6y-1、6y、6y+1、6y+2、6y+3、6y+4（y>=1）

其中，6y、6y+2、6y+3、6y+4都不可能是素數，只有6y-1和6y+1可能是素數。

另外，6y-1（y>=1）和 6y + 5 （y>=0）等價。

所以，我們可以將n不為6y-1（或6y+5）和6y+1的數直接排除，排除方法為，

  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }

下面要剔除掉6y-1（或6y+5）和6y+1中的非素數，

  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }

這裡大家比較疑惑的可能有兩點：

for迴圈i自增為啥是 6
for迴圈中素數判定的條件為啥是 n % i === 0 || n % (i+2) === 0

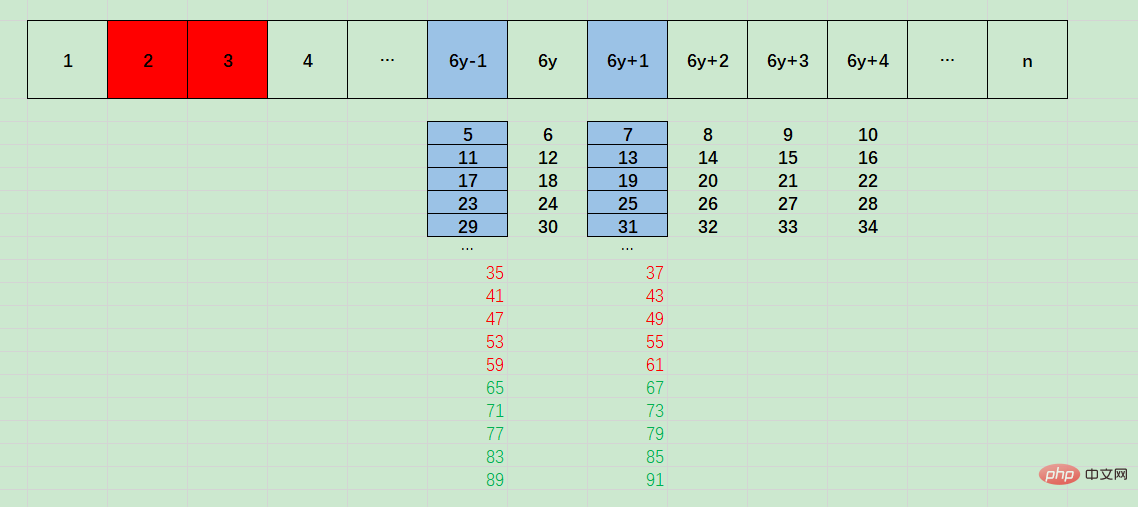
我們看上面圖解，可以發現，6y-1，是基數為5，差值為6的等差數列，即 5 + 6x :

對於 5 + 6x 而言，如果x為5的倍數（5 * z），則5 + 6x = 5 + 6 * 5 * z = 5 *（1+6z）,則此時5 + 6x可以被5整除。
5 + 6x 還可以轉化為 5 + 6 + 6 * (x-1) = 11 + 6(x-1)，則只要x-1為11的倍數，則5 + 6x可以被11整除，
5 + 6x 還可以轉化為 5 + 12 + 6 * (x-2) = 17 + 6(x-2)，則只要x-2為17的倍數，則5 + 6x可以被17整除
......

6y+1，是基數為7，差值為6的等差數列，即 7 + 6x :

對於 7 + 6x 而言，如果x為7的倍數（7 * z），則7 + 6x = 7 + 6 * 7 * z = 7 *（1+6z）,則此時7 + 6x可以被7整除。
7 + 6x 還可以轉化為 7 + 6 + 6 * (x-1) = 13 + 6(x-1)，則只要x-1為13的倍數，則7 + 6x可以被13整除，
7 + 6x 還可以轉化為 7 + 12 + 6 * (x-2) = 19 + 6(x-2)，則只要x-2為19的倍數，則7 + 6x可以被19整除，
......

所以6y-1和6y+1可能整除的數自增量為6，這是for迴圈i自增為啥是 6的原因

且6y-1和6y+1的整除數基數為5和7，相差為2，這是for迴圈中素數判定的條件為啥是 n % i === 0 || n % (i+2) === 0的原因

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }
 
  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }
 
  return true;
}

此時時間複雜度為 O（sqrt(n) / 3）

【相關推薦：、】

以上就是javascript怎麼求素數的詳細內容，更多請關注TW511.COM其它相關文章！