技術背景

在前面幾篇跟SETTLE約束演演算法相關的文章（1, 2, 3）中，都涉及到了大量的向量旋轉的問題--通過一個旋轉矩陣，給定三個空間上的尤拉角\(\alpha, \beta, \gamma\)，將指定的向量繞對應軸進行旋轉操作。而本文主要就闡述這些旋轉操作中，有可能面臨到的一個重要問題--萬向節死鎖問題（Gimbal Lock）。

一般大家覺得用影象化的方式來展示問題會顯得更加的直觀，但是這裡我們準備直接用公式來陳述一下這個問題，也許會更直接。首先我們知道幾個熟悉的旋轉矩陣：

\[R_Y(\alpha)=\left( \begin{matrix} cos\alpha && 0 && sin\alpha\\ 0 && 1 && 0\\ -sin\alpha && 0 && cos\alpha \end{matrix} \right)\\ R_X(\beta)=\left( \begin{matrix} 1 && 0 && 0\\ 0 && cos\beta && -sin\beta\\ 0 && sin\beta && cos\beta \end{matrix} \right)\\ R_Z(\gamma)=\left( \begin{matrix} cos\gamma && -sin\gamma && 0\\ sin\gamma && cos\gamma && 0\\ 0 && 0 && 1 \end{matrix} \right) \]

這些旋轉矩陣分別表示繞\(Y, X, Z\)軸旋轉指定的角度的操作。如果我們將這些旋轉操作按照順序作用在一個向量上，由於矩陣運算的結合律，我們可以得到這樣一個等效的操作矩陣：

\[R(\alpha, \beta, \gamma)=R_Y(\alpha)R_X(\beta)R_Z(\gamma)=\left( \begin{matrix} cos\alpha\ cos\gamma+sin\alpha\ sin\beta\ sin\gamma&-cos\alpha\ sin\gamma+sin\alpha\ sin\beta\ cos\gamma&+sin\alpha\ cos\beta\\ cos\beta\ sin\gamma&cos\beta\ cos\gamma&-sin\beta\\ -sin\alpha\ cos\gamma+cos\alpha\ sin\beta\ sin\gamma&sin\alpha\ sin\gamma+cos\alpha\ sin\beta\ cos\gamma&cos\alpha\ cos\beta \end{matrix} \right) \]

為了簡化寫法，我們可以定義：

\[c_1=cos\alpha=cos(Y), s_1=sin\alpha=sin(Y)\\ c_2=cos\beta=cos(X), s_2=sin\beta=sin(X)\\ c_3=cos\gamma=cos(Z), s_3=sin\gamma=sin(Z) \]

那麼就有：

\[R(\alpha, \beta, \gamma)=\left( \begin{matrix} c_1c_3+s_1s_2s_3&-c_1s_3+s_1s_2c_3&+s_1c_2\\ c_2s_3&c_2c_3&-s_2\\ -s_1c_3+c_1s_2s_3&s_1s_3+c_1s_2c_3&c_1c_2 \end{matrix} \right) \]

其實按照不同的順序進行旋轉的話，得到的結果會有6種可能性：\(R_XR_YR_Z,R_XR_ZR_Y,R_YR_XR_Z,R_YR_ZR_X,R_ZR_XR_Y,R_ZR_YR_X\)，但是這裡一般人為的規定使用\(R_YR_XR_Z\)順規，也就是先繞\(Z\)軸旋轉，再繞\(X\)軸旋轉，最後再繞\(Y\)軸旋轉的順序。

如果這裡假定\(\beta=\frac{\pi}{2}\)，也就是繞\(X\)軸旋轉的角度是90度，那麼得到的新的旋轉矩陣為：

\[R(\alpha, \frac{\pi}{2}, \gamma)=R_Y(\alpha)R_X(\frac{\pi}{2})R_Z(\gamma)=\left( \begin{matrix} c_1c_3+s_1s_3&-c_1s_3+s_1c_3&0\\ 0&0&-1\\ -s_1c_3+c_1s_3&s_1s_3+c_1c_3&0 \end{matrix} \right) \]

再回顧下三角函數公式：

\[sin(a\pm b)=sin(a)cos(b)\pm sin(b)cos(a)\\ cos(a\pm b)=cos(a)cos(b)\mp sin(a)sin(b) \]

代入可得：

\[R(\alpha, \frac{\pi}{2}, \gamma)=\left( \begin{matrix} cos(\alpha-\gamma)&sin(\alpha-\gamma)&0\\ 0&0&-1\\ -sin(\alpha-\gamma)&cos(\alpha-\gamma)&0 \end{matrix} \right) \]

類似地：

\[R(\alpha, -\frac{\pi}{2}, \gamma)=\left( \begin{matrix} cos(\alpha+\gamma)&-sin(\alpha+\gamma)&0\\ 0&0&1\\ -sin(\alpha+\gamma)&-cos(\alpha+\gamma)&0 \end{matrix} \right) \]

到這裡，端倪初現，按照上面的這個公式，改變\(\alpha\)和改變\(\gamma\)的值，得到的效果是一樣的。換句話說，如果在一個尤拉角的旋轉矩陣中，在\(X\)軸的方向將其旋轉了90度之後，接下來不論是繞\(Y\)軸旋轉，還是繞\(Z\)軸旋轉，得到的效果是一樣的。那麼，本來應該是三個方向的自由度，現在變成了兩個，這就是問題所在。

SETTLE約束演演算法的侷限性

這裡我們先回顧一下SETTLE演演算法中的一個環節，這個環節中涉及到了旋轉矩陣的使用。首先是給定一個三角形\(\Delta a_0b_0c_0\)：

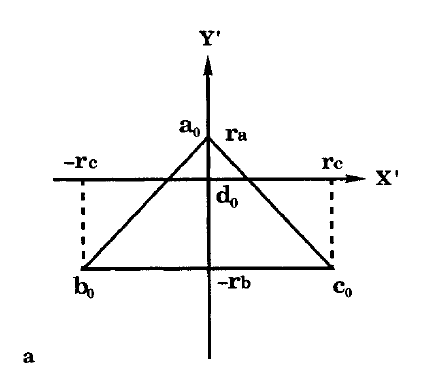
然後將其按照這樣的一個順序進行旋轉操作：

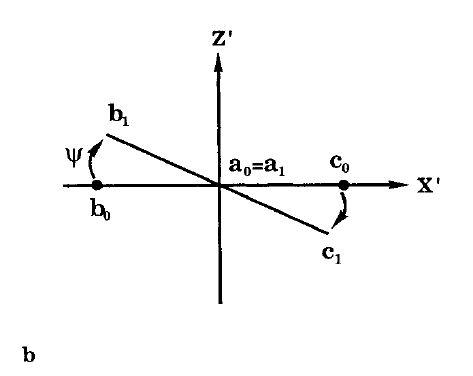
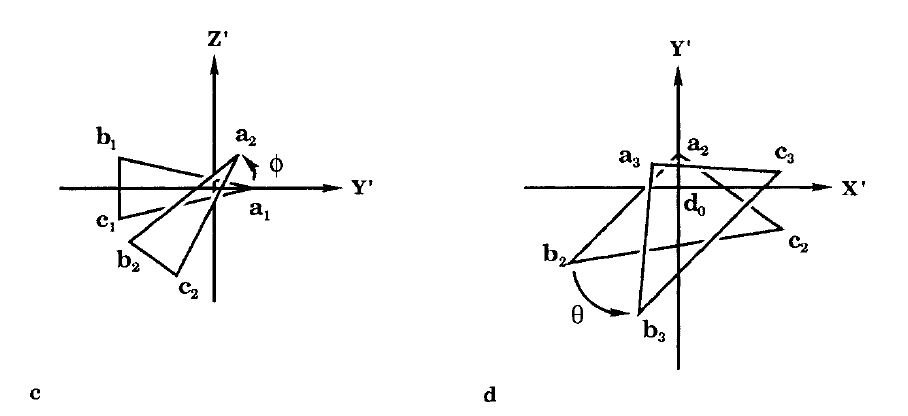
旋轉之後可以得到新的三角形\(\Delta a_3b_3c_3\)。按照SETTLE: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models這篇文章的推導，我們可以得到所需的三個旋轉的尤拉角的計算公式為（這裡有一個需要注意的問題，SETTLE文章裡面的\(\alpha,\beta,\gamma\)三個引數跟我們前面提到的旋轉尤拉角的意義不同，在這篇文章中分別用\(\psi,\phi,\theta\)來表示繞\(Y,X,Z\)軸的旋轉）：

\[\begin{align*} \phi&=arcsin\left(\frac{Z'_{a_3}}{r_a}\right)\\ \psi&=arcsin\left(\frac{Z'_{b_3}-Z'_{c_3}}{2r_ccos\phi}\right)\\ \theta&=arcsin\left(\frac{\gamma}{\sqrt{\alpha^2+\beta^2}}\right)-arctan\left(\frac{\beta}{\alpha}\right) \end{align*} \]

其中\(\alpha\)、\(\beta\)和\(\gamma\)的取值如下：

\[\begin{align*} \alpha&=-r_ccos\psi(X'_{b_0}-X'_{c_0})+(-r_bcos\phi-r_csin\psi sin\phi)(Y'_{b_0}-Y'_{a_0})+(-r_bcos\phi+r_csin\psi sin\phi)(Y'_{c_0}-Y'_{a_0})\\ \beta&=-r_ccos\psi(Y'_{c_0}-Y'_{b_0})+(-r_bcos\phi-r_csin\psi sin\phi)(X'_{b_0}-X'_{a_0})+(-r_bcos\phi+r_csin\psi sin\phi)(X'_{c_0}-X'_{a_0})\\ \gamma&=Y'_{b_1}(X'_{b_0}-X'_{a_0})-X'_{b_1}(Y'_{b_0}-Y'_{a_0})+Y'_{c_1}(X'_{c_0}-X'_{a_0})-X'_{c_1}(Y'_{c_0}-Y'_{a_0}) \end{align*} \]

那麼在這個計算公式中，如果我們取\(X\)軸的旋轉角度為90度，也就是：

\[\phi=\pm\frac{\pi}{2} \]

此時，由於\(cos\phi=0\)，在計算\(\psi\)的時候，就會直接出現報錯，SETTLE演演算法無法繼續執行。那麼在其他類似的尤拉角求解的場景下，一樣有可能出現類似的問題，導致無法正常計算尤拉角。並且，如果給定尤拉角，那麼從原始的向量到終點的向量是一一對應的，但是如果給定兩個向量，其對應的旋轉矩陣不是唯一的。或者說，兩個向量之間變換的軌跡不是唯一的。

Gimbal平衡環架中的死鎖

在參考連結2中，作者自己畫了一個平衡環架用於表示尤拉角死鎖的問題。非常的直觀，本章節中的圖片都來自於參考連結2。首先我們給定一個這樣的Gimbal：

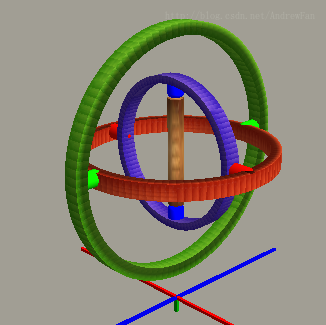
其中每一個顏色的環都可以繞對應軸進行旋轉，比如繞綠軸的旋轉：

繞紅軸的旋轉：

繞藍軸的旋轉：

有了這三個軸的話，不論怎麼旋轉，都可以保持中間那根棍子的位置和朝向不變，達到一個穩定的效果。這個三軸穩定器已經被大量應用在航空航海領域，而後面要講的四元數的概念，其實也是Hamilton在一次坐船的過程中提出來的一個概念。但是有這樣一個特殊的場景，有可能會破壞這個穩定結構。假設我們先把紅色這個圈，旋轉90度到跟藍色圈共面的位置：

那麼接下來我們就會發現，原本在三個軸向的旋轉下都可以保持穩定的棍子，居然搖晃起來了：

這就是有名的萬向節死鎖，死鎖出現的時候，原本三個方向旋轉的自由度，變成了兩個，就失去了一個自由度。接下來我們可以看一看，有沒有什麼方案可以解決萬向節死鎖的問題。

四元數（Quaternion）的定義

應該說，四元數的出現，並不是為了解決尤拉角死鎖的問題。但是在後來長期的應用中，人們發現了四元數在幾何旋轉表示中的獨特優勢。在蛋白質摺疊軟體AlphaFold2和MEGAProtein中都使用到了四元數，用於表徵分子結構的三維旋轉。關於四元數的介紹材料，可以參考一下參考連結3、4，分別是英文版和中文翻譯版。

要理解四元數，至少需要了解複數，可以把四元數當做是複數的一個推廣形式。一個複數是由實部和虛部組成，很多時候我們也會將其寫成指數形式或者是向量形式：

\[z=x+i\ y=\frac{1}{\sqrt{x^2+y^2}}e^{i\ arctan(\frac{y}{x})}=\left[ \begin{matrix} x\\y \end{matrix} \right] \]

其中\(x,y\)是實數，\(x\)稱為複數\(z\)的實部，\(y\)稱為複數\(z\)的虛部，\(i^2=-1\)是虛數單位。正因為複數可以被看做是一個向量，所以我們才會想到複數跟向量旋轉之間的聯絡，比如我們有一個單位長度的複數\(z'=cos\theta+i\ sin\theta\)，那麼就有以下的複數乘法關係：

\[z'z=(cos\theta+i\ sin\theta)(x+i\ y)=xcos\theta+iycos\theta+ixsin\theta-ysin\theta=\left[ \begin{matrix} xcos\theta-ysin\theta\\ ycos\theta+xsin\theta \end{matrix} \right]=\left[ \begin{matrix} cos\theta&-sin\theta\\ sin\theta&cos\theta \end{matrix} \right]\left[ \begin{matrix} x\\y \end{matrix} \right] \]

如此一來，我們就得到了一個二維向量的旋轉矩陣：

\[R_2(\theta)=\left[ \begin{matrix} cos\theta&-sin\theta\\ sin\theta&cos\theta \end{matrix} \right] \]

有了複數的概念基礎，我們可以將其擴充套件成一個四元數：

\[z=x+iy_i+jy_j+ky_k=\left[ \begin{matrix} x\\y_i\\y_j\\y_k \end{matrix} \right] \]

比較特殊的，相比於複數的定義有一些補充定義：

\[i^2=j^2=k^2=ijk=-1\\ ij=k,jk=i,ki=j\\ ji=-k,kj=-i,ik=-j \]

這些關係，其實很容易讓我們聯想到向量的叉乘。類似於單位長度複數的定義，這裡我們可以定義一個單位長度的四元數：

\[\begin{align*} q&=(cos\alpha+j\ sin\alpha)(cos\beta+i\ sin\beta)(cos\gamma+k\ sin\gamma)\\ &=(cos\alpha\ cos\beta\ cos\gamma + sin\alpha\ sin\beta\ sin\gamma)+i(cos\alpha\ sin\beta\ cos\gamma+sin\alpha\ cos\beta\ sin\gamma)+j(sin\alpha\ cos\beta\ cos\gamma-cos\alpha\ sin\beta\ sin\gamma)+k(cos\alpha\ cos\beta\ sin\gamma-sin\alpha\ sin\beta\ cos\gamma)\\ &=(c_1c_2c_3+s_1s_2s_3)+i(c_1s_2c_3+s_1c_2s_3)+j(s_1c_2c_3-c_1s_2s_3)+k(c_1c_2s_3-s_1s_2c_3)\\ &=s+ix+jy+kz \end{align*} \]

這裡我們假定：

\[s=c_1c_2c_3+s_1s_2s_3\\ x=c_1s_2c_3+s_1c_2s_3\\ y=s_1c_2c_3-c_1s_2s_3\\ z=c_1c_2s_3-s_1s_2c_3 \]

因為我們要使得\(q\)是一個單位四元數，因此有：

\[s^2+x^2+y^2+z^2=1 \]

四元數與旋轉矩陣

四元數與複數的旋轉矩陣略有不同，給定一個單位四元數\(q\)和一個三維空間向量（純四元數，即\(s=0\)）：\(\textbf{v}=0+i\ v_i+j\ v_j+k\ v_k\)，那麼向量\(\textbf{v}\)關於\(q\)的旋轉被定義為：\(q\textbf{v}q^{*}\)。這裡\(q^{*}=s-ix-jy-kz\)，是\(q\)的共軛四元數。對於一個單位四元數而言，\(q^{*}=q^{-1}\)。那麼我們可以計算一下對應的旋轉矩陣\(R_q\)：

\[\begin{align*} R_q\textbf{v}&=q\textbf{v}q^{*}\\ &=(s+ix+jy+kz)\left[ v_ix+v_jy+v_kz+i(v_is-v_jz+v_ky)+j(v_iz+v_js-v_kx)+k(-v_iy+v_jx+v_ks) \right]\\ &=\left[ \begin{matrix} s^2+x^2-y^2-z^2&&2xy-2sz&&2xz+2sy\\ 2sz+2xy&&s^2-x^2+y^2-z^2&&2yz-2sx\\ 2xz-2sy&&2sx+2yz&&s^2-x^2-y^2+z^2 \end{matrix} \right]\left[ \begin{matrix} v_i\\v_j\\v_k \end{matrix} \right] \end{align*} \]

即，四元數所代表的旋轉矩陣為：

\[\begin{align*} R(\alpha,\beta,\gamma)&=\left[ \begin{matrix} s^2+x^2-y^2-z^2&&2xy-2sz&&2xz+2sy\\ 2sz+2xy&&s^2-x^2+y^2-z^2&&2yz-2sx\\ 2xz-2sy&&2sx+2yz&&s^2-x^2-y^2+z^2 \end{matrix} \right]\\ &=\left[ \begin{matrix} cos2\alpha\ cos2\gamma+sin2\alpha\ sin2\beta\ sin2\gamma&&sin2\alpha\ sin2\beta\ cos2\gamma-cos2\alpha\ sin2\gamma&&sin2\alpha\ cos2\beta\\ cos2\beta\ sin2\gamma&&cos2\beta\ cos2\gamma&&-sin2\beta\\ cos2\alpha\ sin2\beta\ sin2\gamma-sin2\alpha\ cos2\gamma&&sin2\alpha\ sin2\gamma+cos2\alpha\ sin2\beta\ cos2\gamma&&cos2\alpha\ cos2\beta \end{matrix} \right] \end{align*} \]

可以發現這裡得到的旋轉矩陣跟前面的\(R_YR_XR_Z\)順規結果是一致的。但有一點不同的是，在這個結果中我們還發現了一個比較重要的變換：所有的角度在旋轉矩陣中都翻了1倍。這裡給了我們一個重要啟示：在使用四元數對向量進行旋轉時，需要先把角度除以2。

四元數Python程式碼實現

在Python的符號計算庫Sympy中，已經支援了四元數的相關運算：

from sympy import *
from sympy.algebras.quaternion import Quaternion

s, x, y, z = symbols('s x y z', real=True, positive=True)
a, b, g = symbols('a b g')
vi, vj, vk = symbols('v_i v_j v_k')
tvi, tvj, tvk = symbols('t_i, t_j, t_k')

# 定義三個軸的旋轉四元數
qa = Quaternion(cos(a), 0, sin(a), 0)
qb = Quaternion(cos(b), sin(b), 0, 0)
qg = Quaternion(cos(g), 0, 0, sin(g))

# 按順序合併旋轉四元數為一個單位四元數
q = qa.mul(qb.mul(qg))

print ('The unit quaternion q is: {}'.format(pretty(q)))
# The quaternion q is: (sin(a)*sin(b)*sin(g) + cos(a)*cos(b)*cos(g)) + (sin(a)*sin(g)*cos(b) + sin(b)*cos(a)*cos(g))*i +
# (sin(a)*cos(b)*cos(g) - sin(b)*sin(g)*cos(a))*j + (-sin(a)*sin(b)*cos(g) + sin(g)*cos(a)*cos(b))*k

# 定義一個普通四元數
q = Quaternion(s, x, y, z)
print ('The normal quaternion q is: {}'.format(pretty(q)))
# The normal quaternion q is: s + x*i + y*j + z*k

# 四元數求共軛
cq = conjugate(q)
print ('The conjugate quaternion cq is: {}'.format(pretty(cq)))

# 定義一個純四元數
v = Quaternion(0, vi, vj, vk)
print ('The pure quaternion v is: {}'.format(pretty(v)))
# The pure quaternion v is: 0 + v_i*i + v_j*j + v_k*k

# 計算四元數的旋轉qvq*
tv = simplify(q.mul(v.mul(cq)))
print ('Transformed pure quaternion tv is: {}'.format(pretty(tv)))
# Transformed pure quaternion tv is: 0 +
# (s*(s*v_i - v_j*z + v_k*y) + x*(v_i*x + v_j*y + v_k*z) + y*(s*v_k - v_i*y + v_j*x) - z*(s*v_j + v_i*z - v_k*x))*i +
# (s*(s*v_j + v_i*z - v_k*x) - x*(s*v_k - v_i*y + v_j*x) + y*(v_i*x + v_j*y + v_k*z) + z*(s*v_i - v_j*z + v_k*y))*j +
# (s*(s*v_k - v_i*y + v_j*x) + x*(s*v_j + v_i*z - v_k*x) - y*(s*v_i - v_j*z + v_k*y) + z*(v_i*x + v_j*y + v_k*z))*k

那麼有了Sympy這樣強大的四元數處理的工具，可以節省我們很多手算的時間。

四元數是否解決了Gimbal Lock問題？

在最前面的章節中，我們講Gimbal Lock尤拉角死鎖問題時，提到了一個比較重要的點：在特定條件下（如繞一個指定的軸旋轉90度），兩個空間向量中間可以對應無窮多個尤拉角的組合。這個現象也體現出了，用尤拉角的方式無法一一對應的表示每兩個空間向量之間的旋轉關係。因此我們需要找到一個新的表示方法，基於新的表示方法，不僅要使得每一組輸入引數對應一個特定的旋轉，還需要使得給定任意的兩個空間向量，所計算得到的引數要是唯一的，這樣才能構成一一對應的對映關係。我們先介紹一下從兩個空間向量\(\textbf{v}_1, \textbf{v}_2\)中去計算四元數的方法，再結合一些實際案例，看看是否會出現尤拉角旋轉矩陣中出現的奇點。

假設兩個向量之間的夾角為\(\theta\)，則對應的旋轉四元數可以表示為：

\[\textbf{u}=\textbf{v}_1\times\textbf{v}_2\\ cos\theta=\frac{\textbf{v}_1\cdot\textbf{v}_2}{|\textbf{v}_1||\textbf{v}_2|}\\ q=cos\frac{\theta}{2}+i\ sin\frac{\theta}{2}\textbf{u}\cdot i+j\ sin\frac{\theta}{2}\textbf{u}\cdot j+k\ sin\frac{\theta}{2}\textbf{u}\cdot k \]

案例重現

那麼如果我們使用前面提到的尤拉角奇點的案例，假定一個空間向量\(\textbf{v}_0=i\)，也就是處於三維座標系的X軸正方向上的一個單位向量，我們給它設計一個路徑：先繞Z軸旋轉\(\gamma\)的角度，然後繞X軸旋轉90度，最後再繞Y軸旋轉\(\alpha\)的角度，那麼對應的四元數為：

\[\begin{align*} q&=(cos\frac{\alpha}{2}-j\ sin\frac{\alpha}{2})(\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2})(cos\frac{\gamma}{2}+k\ sin\frac{\gamma}{2})\\ &=\frac{\sqrt{2}}{2}\left[ cos(\frac{\alpha}{2}+\frac{\gamma}{2})+i\ cos(\frac{\alpha}{2}+\frac{\gamma}{2})-j\ sin(\frac{\alpha}{2}+\frac{\gamma}{2})+k\ sin(\frac{\alpha}{2}+\frac{\gamma}{2}) \right] \end{align*} \]

因為在四元數中我們並不關心具體每個旋轉角度的值，我們只需要四元數的四個元素就可以了，所以這裡令\(x=cos(\frac{\alpha}{2}+\frac{\gamma}{2}), y=sin(\frac{\alpha}{2}+\frac{\gamma}{2})\)，則有：

\[q=\frac{\sqrt{2}}{2}(x+ix-jy+ky)\\ x^2+y^2=1 \]

使用Hamilton Product作用在\(\textbf{v}_0\)上可以得到：

\[\textbf{v}_1=q\textbf{v}_0q^{*}=i(x^2-y^2)+2kxy \]

為了簡化計算量，假定我們得到的結果是\(\textbf{v}_1=k\)，在三維座標系下，這個向量位於\(Z\)軸的正方向上，也就是：

\[\textbf{v}_1=q\textbf{v}_0q^{*}=i(x^2-y^2)+2kxy=k \]

則有對應關係：

\[\left\{ \begin{matrix} x^2-y^2=0\\ x^2+y^2=1\\ xy=\frac{1}{2} \end{matrix} \right. \]

那麼得到兩組解：

\[\left\{ \begin{matrix} x=\frac{\sqrt{2}}{2}, y=\frac{\sqrt{2}}{2}\\ x=-\frac{\sqrt{2}}{2}, y=-\frac{\sqrt{2}}{2} \end{matrix} \right. \]

也就是說，這個旋轉過程有兩個可能對應的四元數：

\[\left\{ \begin{matrix} q_1=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i-\frac{\sqrt{2}}{2}j+\frac{\sqrt{2}}{2}k\\ q_2=-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i+\frac{\sqrt{2}}{2}j-\frac{\sqrt{2}}{2}k \end{matrix} \right. \]

而在這個計算過程中，我們依然發現，如果使用尤拉角來進行旋轉的話，只能計算出\(\alpha+\gamma\)的值，但是法對其進行求解，而四元數則不存在這樣的奇點。

案例拓展

在上面這個案例中，我們其實是已經給定了一個軌跡所對應的四元數。而如果只是知道起始點\(i\)和終點\(k\)，其實我們也可以用上述計算旋轉四元數的方法來進行求解：

\[\textbf{u}=i\times k=-j\\ cos\theta=i\cdot k=0\\ \]

這就可以計算得四元數：

\[\begin{align*} q&=cos\frac{\theta}{2}+i\ sin\frac{\theta}{2}\textbf{u}\cdot i+j\ sin\frac{\theta}{2}\textbf{u}\cdot j+k\ sin\frac{\theta}{2}\textbf{u}\cdot k\\ &=\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}j \end{align*} \]

雖然這個計算過程很容易，但是我們依然可以使用sympy來驗算一下：

In [1]: from sympy import *

In [2]: from sympy.algebras.quaternion import Quaternion

In [3]: import numpy as np

In [4]: q=Quaternion(np.sqrt(2)/2,0,-np.sqrt(2)/2,0)

In [5]: v=Quaternion(0,1,0,0)

In [6]: q.mul(v.mul(conjugate(q)))
Out[6]: 0 + 0*i + 0*j + 1.0*k

類似的，我們也可以驗證一下上一個模組中提到的指定軌跡和起始點與終點所得到的旋轉四元數：

In [7]: q=Quaternion(np.sqrt(2)/2,np.sqrt(2)/2,-np.sqrt(2)/2,np.sqrt(2)/2)/np.sqrt(2)

In [8]: q.mul(v.mul(conjugate(q)))
Out[8]: 0 + 0*i + 0*j + 1.0*k

In [9]: q=-1*Quaternion(np.sqrt(2)/2,np.sqrt(2)/2,-np.sqrt(2)/2,np.sqrt(2)/2)/np.sqrt(2)

In [10]: q.mul(v.mul(conjugate(q)))
Out[10]: 0 + 0*i + 0*j + 1.0*k

總結概要

本文通過兩個案例——旋轉矩陣和分子動力學模擬中的SETTLE約束演演算法，介紹了一下Gimbal Lock問題，簡單來說就是，用旋轉矩陣去表示三維空間的向量旋轉有可能會遇到奇點，使得三維空間原本的三個自由度在某一個點變成兩個自由度。而使用我們這裡所介紹的四元數Quaternion則不會有這樣的問題，同時本文也介紹了一些四元數的基本運演演算法則和sympy中的程式碼實現。後續會再單獨寫三篇部落格介紹一下四元數的具體運算細則、四元數在SETTLE演演算法中的應用以及四元數的物理含義等，敬請期待。

版權宣告

本文首發連結為：https://www.cnblogs.com/dechinphy/p/quaternion.html

作者ID：DechinPhy

更多原著文章請參考：https://www.cnblogs.com/dechinphy/

打賞專用連結：https://www.cnblogs.com/dechinphy/gallery/image/379634.html

騰訊雲專欄同步：https://cloud.tencent.com/developer/column/91958

CSDN同步連結：https://blog.csdn.net/baidu_37157624?spm=1008.2028.3001.5343

51CTO同步連結：https://blog.51cto.com/u_15561675