論文資訊

論文標題：GCAN: Graph-aware Co-Attention Networks for Explainable Fake News Detection on Social Media
論文作者：Yi-Ju Lu, Cheng-Te Li
論文來源：2020, ACL
論文地址：download 
論文程式碼：download 

1 Abstract 

　　目的：預測源推文是否是假的，並通過突出顯示可疑的轉發者上的證據和他們所關心的詞語來產生解釋。

2 Introduction

　　我們預測一個源推文故事是否是假，根據它的短文內容和使用者轉發序列，以及使用者個人資料。

　　我們在三種設定下檢測假新聞：   (a) short-text source tweet (b) no text of user comments (c) no network structures of social network and diffusion network.

　　本文貢獻：

　　(1) 研究了一種新穎、更現實的社交媒體上的假新聞檢測場景；

　　(2) 為了準確的檢測，我們開發了一個新的模型，GCAN，以更好地學習使用者互動的表示、轉發傳播及其與源短文的相關性；

　　(3) 本文的雙重共同注意機制可以產生合理的解釋；

　　(4) 在真實資料集上進行的大量實驗證明，與最先進的模型相比，GCAN具有良好的效能前景；

3 Related Work

　　

4 Problem Statement

　　

5 GCAN Model

　　總體框架如下：

　　

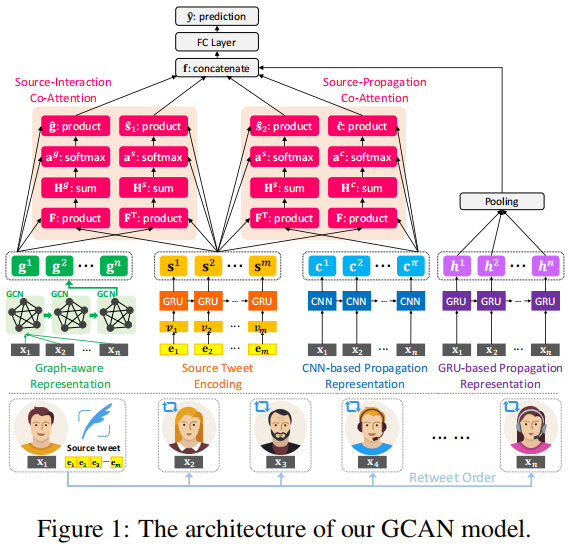
　　GCAN 包括五個部分：

• 1. user characteristics extraction: creating features to quantify how a user participates in online social networking.
  2. new story encoding: generating the representation of words in the source tweet.
  3. user propagation representation : modeling and representing how the source tweet propagates by users using their extracted characteristics.
  4. dual co-attention mechanisms: capturing the correlation between the source tweet and users’ interactions/propagation.
  5. making prediction: generating the detection outcome by concatenating all learned representations.

5.1 User Characteristics Extraction

　　使用者 $u_{j}$ 的特徵為 $\mathbf{x}_{j} \in \mathbb{R}^{v}$：

　　(1) number of words in a user's self-description；
　　(2) number of words in $u_{j} 's$ screen name；
　　(3) number of users who follows $u_{j}$；
　　(4) number of users that $u_{j}$ is following；
　　(5) number of created stories for $u_{j}$ ；
　　(6) time elapsed after $u_{j} 's$ first story；
　　(7) whether the $u_{j}$ account is verified or not；
　　(8) whether $u_{j}$ allows the geo-spatial positioning；
　　(9) time difference between the source tweet's post time and $u_{j} 's$ retweet time；
　　(10) the length of retweet path between $u_{j}$ and the source tweet (1 if $u_{j}$ retweets the source tweet)；

5.2 Source Tweet Encoding

　　輸入是 story $s_{i}$ 中每個單詞的一個熱向量。由於每個 source story 的長度都是不同的，所以在這裡通過設定最大長度 $m$ 來執行零填充。設 $\mathbf{E}=\left[e_{1}, e_{2}, \ldots, e_{m}\right] \in \mathbb{R}^{m}$ 為 source story 的輸入向量，其中 $e_{m}$ 為第 $m$ 個單詞的獨熱編碼。我們建立了一個完全連線的層來生成單詞嵌入，$\mathbf{V}=\left[\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{m}\right] \in \mathbb{R}^{d \times m}$，其中 $d$ 是單詞嵌入的維數。$V$ 的推導方法為：

　　　　$\mathbf{V}=\tanh \left(\mathbf{W}_{w} \mathbf{E}+\mathbf{b}_{w}\right)  \quad\quad\quad(1)$

　　其中，$\mathbf{W}_{w}$ 為可學習權值的矩陣，$\mathbf{b}_{c}$ 為偏差項。然後，利用門控迴圈單元（GRU）從 $v$ 學習單詞序列表示。源推文表示學習可以用：$\mathbf{s}_{t}=G R U\left(\mathbf{v}_{t}\right), t \in\{1, \ldots, m\} \mid$，其中 $m$ 是 GRU 維數。將源推文表示為 $\mathbf{S}=\left[\mathbf{s}^{1}, \mathbf{s}^{2}, \ldots, \mathbf{s}^{m}\right] \in \mathbb{R}^{d \times m}$。

5.3 User Propagation Representation

　　隨著時間的推移，源推文 $s_i$ 的傳播是由一系列的使用者觸發的。我們的目的是利用提取的使用者特徵向量 $x_j$，以及使用者序列擴充套件$s_i$，來學習使用者傳播表示。

　　本文利用門控遞迴單元（GRU）和折積神經網路（CNN）來學習傳播表示。

　　這裡輸入的是使用者轉發 $s_{i}$ 的特徵向量序列，用 $P F\left(s_{i}\right)=   \left\langle\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{t}, \ldots, \mathbf{x}_{n}\right\rangle$ 表示，其中 $n$ 是觀察到的轉發的固定長度。如果共用 $s_{i}$ 的使用者數量大於 $n$，我們取前 $n$ 個使用者。如果這個數位小於 $n$，我們在 $P F（si）$ 中重新取樣使用者，直到它的長度等於 $n$。 

GRU-based Representation
　　給定特徵向量 $PF(s_{i})=\langle\ldots, \mathbf{x}_{t}, \ldots\rangle$ 的序列，我們利用 GRU 來學習傳播表示。每個 GRU 狀態都有兩個輸入，當前的特徵向量 $\mathbf{x}_{t}$ 和前一個狀態的輸出向量 $\mathbf{h}_{t-1}$，和一個輸出向量 $\mathbf{h}_{t-1}$。基於GRU的表示學習可以用： $\mathbf{h}_{t}=G R U\left(\mathbf{x}_{t}\right), t \in\{1, \ldots, n\}$ 來表示，其中 $n$ 是GRU的維數。我們通過平均池化生成最終的基於 GRUs 的使用者傳播嵌入 $\mathbf{h} \in \mathbb{R}^{d}$，由 $\mathbf{h}=\frac{1}{n} \sum_{t=1}^{n} \mathbf{h}_{t}$ 給出。

CNN-based Representation.

　　本文利用一維折積神經網路來學習 $PF\left(s_{i}\right)$ 中使用者特徵的序列相關性。本文一次性考慮 $\lambda$ 個連續使用者來建模他們的序列相關性，即 $\left\langle\mathbf{x}_{t}, \ldots, \mathbf{x}_{t+\lambda-1}\right\rangle$。因此，過濾器被設定為Wf∈Rλ×v。然後輸出表示向量 $\mathbf{C} \in \mathbb{R}^{d \times(t+\lambda-1)}$ 由

　　　　$\mathbf{C}=\operatorname{ReLU}\left(\mathbf{W}_{f} \cdot \mathbf{X}_{t: t+\lambda-1}+b_{f}\right)$

　　其中 $\mathbf{W}_{f}$ 為可學習引數的矩陣，ReLU 為啟用函數，$\mathbf{X}_{t: t+\lambda-1}$ 描述了第一行索引從 $t=1$ 到$t=n-\lambda+1$ 的子矩陣，$b_{f}$ 為偏差項。

5.4 Graph-aware Propagation Representation

　　我們的目的是建立一個圖來建模轉發使用者之間潛在的互動，想法是擁有特殊特徵的使用者之間的相關性對揭示源推文是否是假新聞能夠起到作用。每個源推文 $s_{i}$ 的轉發使用者集合 $U_{i}$ 都被用來構建一個圖 $\mathcal{G}^{i}=\left(U_{i}, \mathcal{E}_{i}\right)$ 。由於使用者間的真實互動是不清楚的，因而這個圖是全連線的，也 就是任意節點相連， $\left|\mathcal{E}_{i}\right|=\frac{n \times(n-1)}{2}$ 。結合使用者特徵，每條邊 $e_{\alpha \beta} \in \mathcal{E}_{i}$ 都被關聯到 一個權重 $w_{\alpha \beta}$，這個權重也就是節點使用者特徵向量 $x_{\alpha}$ 和 $x_{\beta}$ 的餘弦相似度，即 $w_{\alpha \beta}=\frac{x_{\alpha} \cdot x_{\beta}}{\left\|x_{\alpha}\right\|\left\|x_{\beta}\right\|}$ ，圖的鄰接矩陣 $A=\left[w_{\alpha \beta}\right] \in \mathbb{R}^{n \times n}$。

　　然後使用 GCN 來學習使用者互動表示。給定鄰接矩陣 $A$ 和使用者特徵矩陣 $X$ ，新的 $g$ 維節 點特徵矩陣 $H^{(l-1)} \in \mathbb{R}^{n \times g}$ 計算過程為:

　　　　$\mathbf{H}^{(l+1)}=\rho\left(\tilde{\mathbf{A}} \mathbf{H}^{(l)} \mathbf{W}_{l}\right)$

　　$l$  是層數，$\tilde{A}=D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$，$D_{i i}=\sum_{j} A_{i j}$  是度矩陣，$W_{l} \in \mathbb{R}^{d \times g}$  是第  $l$  層的學習引數，  $\rho$  是啟用函數。這裡  $H^{0}=X$  ，實驗時選擇堆疊兩層  $\mathrm{GCN}$  層，最終學習到的表示為  $G \in \mathbb{R}^{g \times n} $。

5.5 Dual Co-attention Mechanism

　　我們認為假新聞的證據可以通過調查源推文的哪些部分是由哪些型別的轉發使用者關注的來揭開，並且線索可以由轉發使用者之間如何互動來反映。因此，本文提出了 dual co-attention 機制，來建模：
　　① 源推文 $\left(S=\left[s^{1}, s^{2}, \cdots, s^{m}\right]\right)$ 與使用者傳播 Embedding $\left(C=\left[c^{1}, c^{2}, \cdots, c^{n-\lambda+1}\right]\right.$ ) 之間

　　② 源推文 $\left(S=\left[s^{1}, s^{2}, \cdots, s^{m}\right]\right)$ 與 graph-aware 的 Embedding 互動 （$G=[g^{1}, g^{2}, \cdots, g^{n}]$) 之間

　　通過 dual co-attention 的注意力權重，模型可以具有可解釋性。

Source-Interaction Co-attention

　　首先計算一個相似性矩陣 $F \in \mathbb{R}^{m \times n} :$

　　　　$F=\tanh \left(S^{T} W_{s g} G\right)$

　　這裡 $W_{s g}$ 是一個 $d \times g$ 的引數矩陣，接著按照以下方式得到 $H^{s}$ 和 $H^{g}$ 。

　　　　$\begin{array}{l}\mathbf{H}^{s}=\tanh \left(\mathbf{W}_{s} \mathbf{S}+\left(\mathbf{W}_{g} \mathbf{G}\right) \mathbf{F}^{\top}\right) \\\mathbf{H}^{g}=\tanh \left(\mathbf{W}_{g} \mathbf{G}+\left(\mathbf{W}_{s} \mathbf{S}\right) \mathbf{F}\right)\end{array}   \quad\quad\quad(4)$

　　這裡  $W_{s} \in \mathbb{R}^{k \times d}$， $W_{g} \in \mathbb{R}^{k \times g}$  ，這裡的  $F$  和  $F^{T}$  可以看做在做 user-interaction attention 空間和 source story word attention 空間的轉換。接下來得到 attention 的權重:

　　　　$\begin{array}{l}\mathbf{a}^{s}=\operatorname{softmax}\left(\mathbf{w}_{h s}^{\top} \mathbf{H}^{s}\right) \\\mathbf{a}^{g}=\operatorname{softmax}\left(\mathbf{w}_{h g}^{\top} \mathbf{H}^{g}\right)\end{array}  \quad\quad\quad(5)$

　　這裡  $a^{s} \in \mathbb{R}^{1 \times m}$，$a^{g} \in \mathbb{R}^{1 \times n}$ ， $w_{h s}, w_{h g} \in \mathbb{R}^{1 \times k} $ 是學習的引數。最後可以得到源倠文 和使用者互動的 attention 向量：

　　　　$\hat{\mathbf{s}}_{1}=\sum\limits_{i=1}^{m} \mathbf{a}_{i}^{s} \mathbf{s}^{i}, \quad \hat{\mathbf{g}}=\sum\limits_{j=1}^{n} \mathbf{a}_{j}^{g} \mathbf{g}^{j} \quad\quad\quad(6)$

　　$\hat{s}_{1}$ 和 $\hat{g}$ 描述源推文中的單詞是如何被使用者參與互動的。

Source-Propagation Co-attention.

　　按照上述類似過程生成 $S$ 和 $C$ 的 attention 向量 $\hat{s}_{2}$ 和 $\hat{c}$。

　　注意基於 GRU 的傳播表示沒有用來學習與 $S$ 的互動。這是因為對於假新聞的預測來說，轉發序列的使用者特徵能夠起到重要的作用。因此本文采用基於 GRU 和 CNN 的兩種方式來學習傳播表 示，其中基於 CNN 的傳播表示被用來學習與 S 的互動，基於 GRU的傳播表示在進行最終預測時 用作最終分類器的直接輸入。

5.6 Make Prediction

　　最終使用 $f=\left[\hat{s}_{1}, \hat{g}, \hat{s}_{2}, \hat{c}, h\right]$ 來進行假新聞檢測: 

　　　　$\hat{y}=\operatorname{softmax}\left(\operatorname{Re} L U\left(f W_{f}+b_{f}\right)\right)$

　　損失函數採用交叉熵損失：

　　　　$\mathcal{L}(\Theta)=-y \log \left(\hat{y}_{1}\right)-(1-y) \log \left(1-\hat{y}_{0}\right)$

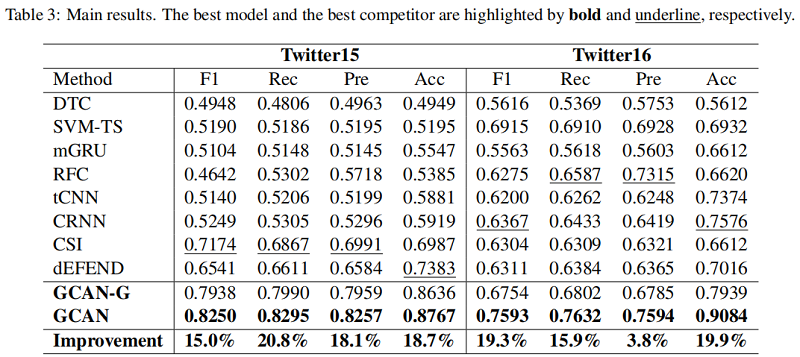
6 Experiments

Baseline：

　　

 

假新聞早期檢測
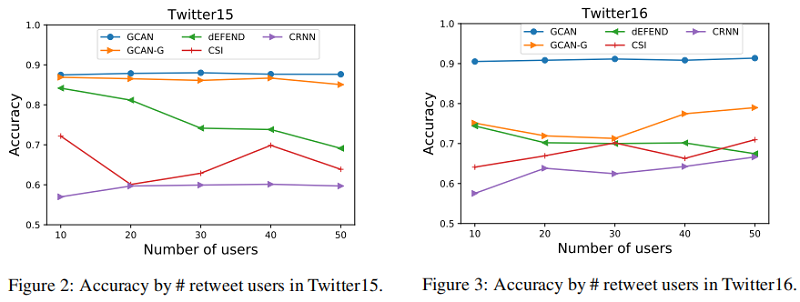
　　GCAN也可以用於假新聞早期的檢測，也就是在轉發使用者不多的時候進行檢測，實驗改動了使用的轉發使用者數量來進行驗證：

　　

 

消融實驗

　　另外移除了一部分元件進行了消融實驗，圖中 -A,-R,-G,-C 分別代表 移除dual co-attention，基於GRU的表示，graph-aware的表示和基於CNN的表示：

　　

 

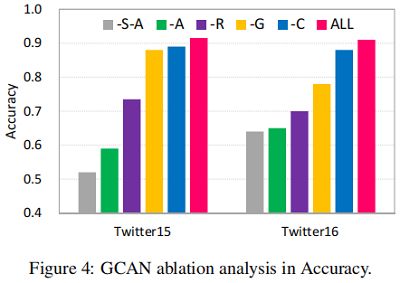
 　　-S-A 代表既沒有源推文 Embedding 也沒有 dual co-attention，由於源推文提供了基本線索，因此 -S-A 有一個明顯的效能下降。

可解釋性
　　source-propagation co-attention 學習到的 attention 權重可以用來為預測假新聞提供證據，採用的方式就是標識出源推文中的重要的詞和可疑的使用者。注意，我們不考慮 source-interaction Co-attention 的可解釋性，因為從構造的圖中學到的使用者互動特徵不能直觀地解釋。

　　下圖是根據對源推文中的 attention 權重繪製的兩個例子的詞雲（權重越大，詞雲中的詞就越大）：

　　

　　圖中結果滿足常識，也就是假新聞傾向於使用戲劇性和模糊的詞彙，而真實新聞則是被證實和核實事實的相關詞彙。

　　另外我們希望利用傳播中的轉發順序來揭示假新聞與真新聞的行為差異。下圖採集並展示了三個假新聞和三個真新聞的傳播序列 attention 的權重：

　　

 

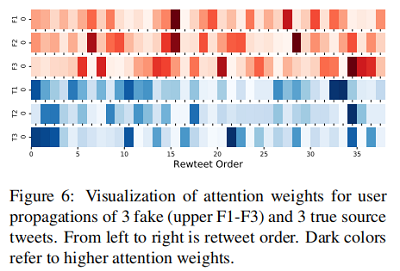
　　結果表明，要確定一個新聞是否虛假，首先應該檢查早期轉發源推文的使用者的特徵。假新聞的使用者 attention 權重可能在傳播過程中均勻分佈。

　　source-propagation co-attention可以進一步解釋可疑使用者的特徵及其關注的詞語，舉例如下圖：

　　

　　可以發現，可疑使用者在轉發傳播中的特徵有：
　　①賬號未被驗證；
　　②賬號建立時間較短；
　　③使用者描述長度較短；
　　④距釋出源推文使用者的圖路徑長度較短。

　　他們高度關注的詞是「breaking」和「pipeline」這樣的詞。我們認為這樣的解釋有助於解讀假新聞的檢測，從而瞭解他們潛在的立場。