累加和為 K 的最長子陣列問題

作者：Grey

原文地址：

部落格園：累加和為 K 的最長子陣列問題

CSDN：累加和為 K 的最長子陣列問題

題目描述

給定一個整陣列成的無序陣列 arr，值可能正、可能負、可能0，給定一個整數值 K，找到 arr 的所有子陣列裡，哪個子陣列的累加和等於 K，並且是長度最大的，返回其長度。

OJ 見：LintCode 911 · Maximum Size Subarray Sum Equals k

主要思路

使用雜湊表，key 存累加和，value 存當前位置，所以，

map.put(sum,i)

表示0...i的累加和是sum。

有了這個雜湊表，我們可以繼續遍歷陣列，當遍歷到i位置的時候，我們可以得到當前的累加和是sum，我們期待雜湊表中是否存在sum - k的記錄，如果有，說明

i - map.get(sum - k)就是一個可能的答案，範例圖如下

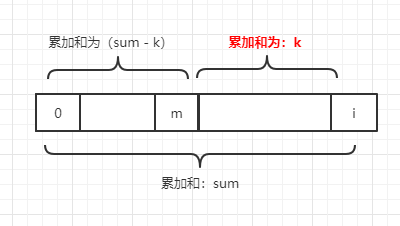
我們每次來到一個i位置，就要定位上圖中m的位置，即i - map.get(sum-k)的值。

然後和全域性答案進行比較，抓取最大長度即可。

程式碼見：

public class Solution {
    public static int maxSubArrayLen(int[] arr, int k) {
        if (arr == null) {
            return 0;
        }
        Map<Integer, Integer> map = new HashMap<>();
        map.put(0, -1);
        int ans = 0;
        int sum = 0;
        for (int i = 0; i < arr.length; i++) {
            sum += arr[i];
            // 期待map裡面有sum - k的記錄
            if (map.containsKey(sum - k)) {
                ans = Math.max(ans, i - map.get(sum - k));
            }
            if (!map.containsKey(sum)) {
                map.put(sum, i);
            }
        }
        return ans;
    }
}

注：map.put(0, -1);這一句很有必要，表示在一個元素都沒有的情況下，已經可以得到一個累加和為 0 的陣列了。

整個演演算法的時間複雜度是O(N)，空間複雜度O(N)。

有了上述演演算法模型，面對這題: LeetCode 525. Contiguous Array

給定一個整陣列成的無序陣列 arr，值可能正、可能負、可能0，找到 arr 的所有子陣列裡，陣列中 1 和 0 一樣多的子陣列最長的長度

只需要預處理一下原陣列，遇到0變為-1，遇到1保持1，遇到其他變為0，接下來求子陣列之和為0的最大子陣列長度，複用上述演演算法模板即可。

程式碼如下

class Solution {
  public static int findMaxLength(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == 0) {
                arr[i] = -1;
            }
        }
        // 轉換為累加和等於K的最長子陣列長度
        Map<Integer, Integer> map = new HashMap<>(arr.length);
        map.put(0, -1);
        int ans = 0;
        int sum = 0;
        for (int i = 0; i < arr.length; i++) {
            sum += arr[i];
            if (map.containsKey(sum)) {
                ans = Math.max(ans, i - map.get(sum));
            }
            if (!map.containsKey(sum)) {
                map.put(sum, i);
            }
        }
        return ans;
    }
}

演演算法和資料結構筆記

累加和為 K 的最長子陣列問題

累加和為 K 的最長子陣列問題

更多