C++ "鏈鏈"不忘@必有迴響之單連結串列
1. 前言
陣列和連結串列是資料結構的基石,是邏輯上可描述、物理結構真實存在的具體資料結構。其它的資料結構往往在此基礎上賦予不同的資料操作語意,如棧先進後出,佇列先進先出……
陣列中的所有資料儲存在一片連續的記憶體區域;連結串列的資料以結點形式儲存,結點分散在記憶體的不同位置,結點之間通過儲存彼此的地址從而知道對方的存在。
因陣列物理結構的連續特性,其查詢速度較快。但因陣列的空間大小是固定的,在新增、插入資料時,可能需要對空間進行擴容操作,刪除時,需要對資料進行移位元運算,其效能較差。
連結串列中的結點通過地址彼此聯絡,查詢有點繁瑣,查詢過程有點像古時候通過烽火傳遞軍情一樣。而插入、刪除操作則較快,只需要改變結點之間的地址資訊就可以。
可認為連結串列是由結點組成的集合實體,根據結點中儲存資訊的不同,可把連結串列分成:
- 單連結串列:結點中儲存資料和其後驅結點的地址。
- 迴圈連結串列:在單連結串列的基礎上,其最後一個結點,也稱尾結點中儲存頭結點的地址,形成一個閉環。
- 雙向連結串列:結點中儲存資料和前、後驅結點的地址。
- 雙向迴圈連結串列:在雙向連結串列的基礎上,頭結點儲存尾結點地址,尾結點儲存頭結點地址。一般說雙向連結串列都是指雙向迴圈連結串列。
在連結串列的基本形式之上,可以根據需要在結點上新增更多資訊,如十字連結串列等複雜形式。在連結串列基礎認知之上,請不要拘泥於知識本身,而要善於根據實際需要進行變通。
本文聊聊基於單連結串列形式的資料查詢、插入、刪除操作。
2. 單連結串列
單連結串列的特點是結點中僅儲存資料本身以及後驅結點的地址,所以單連結串列的結點只有 2 個域:
- 存放資料資訊,稱為資料域。
- 存放後驅結點的地址資訊,稱為指標域。
如下圖描述了單連結串列結點的儲存結構:

C++中可以使用結構體描述結點:
typedef int dataType;
//結點
struct LinkNode{
//資料成員
dataType data;
//後驅結點的地址
LinkNode *next;
//建構函式
LinkNode(dataType data) {
this->data=data;
this->next=NULL;
}
};
當結點與結點之間手牽手後,就構成了連結串列:

連結串列有 2 個特殊結點:
- 頭結點:連結串列的第一個結點,頭結點沒有前驅結點。頭結點可以儲存資料,也可以不儲存資料,不儲存時,此結點為標識用的空白結點,可在連結串列操作時提供便利。關於第一結點的問題在後文會詳細介紹。
- 尾結點:連結串列中的最後一個結點,在單連結串列中其後驅結點的地址為
NULL,也就是沒有後驅結點。
連結串列需要一個LinkNode型別的變數(head)用來儲存頭結點地址,對於整個連結串列的操作往往都是從head儲存的頭結點開始。
連結串列還應該提供維護整個結點鏈路的基本操作演演算法(抽象資料結構):
/*
* 連結串列類
*/
class LinkList {
private:
//頭指標
LinkNode *head;
//連結串列的長度
int length;
public:
//建構函式
LinkList() {}
//返回頭指標
LinkNode * getHead() {
return this->head;
}
//初始化連結串列
void initLinkList() {}
//按位元置查詢結點
LinkNode * findNodeByIndex(int index) {}
//從頭建立連結串列
void createFromHead(int n) {}
//從尾建連結串列
void createFromTail(int n) {}
//按值查詢結點
LinkNode * findNodeByVal(dataType val) {}
//後插入
int instertAfter(dataType val,dataType data) {}
//前插入
int insertBefore(dataType val,dataType data) {}
//按位元置刪除結點
int delNode(dataType data) {}
//刪除所有結點
void delAll() {}
//顯示所有
void showSelf() {}
//解構函式
~LinkList() {
this->delAll();
}
};
2.1 初始化
連結串列由多個結點組成,因頭結點沒有前驅結點,所以需要一個變數儲存其地址,此變數稱為連結串列的head首地址。後續操作基本都是順著首地址"順滕摸瓜"。
當head為NULL時,說明此連結串列為空連結串列。一般會在初始化時,為head變數儲存一個沒有實際資料語意的標誌性結點,也稱為空白頭結點。
所以初始化時,會有 2 種方案:
- 設定
head為NULL。建立一個空連結串列。

//初始化連結串列
void initLinkList() {
this->head=NULL;
}
- 設定
head指向一個沒有實際資料語意的空白結點,此結點僅起到標誌作用。

//初始化連結串列
void initLinkList() {
this->head=new LinkNode(0);
}
是否一定要提供一個標誌性的空白頭結點,這不是必須的,但是有了這個空白頭結點後,會為連結串列的操作帶來諸多的便利性。一般在描述連結串列時,都會提供空白頭結點。
2.2 建立單連結串列
建立單連結串列有 2 種方案:
- 建立過程中,新結點替換原來的頭結點,成為新的頭結點,也稱為頭部插入建立方案。如構建資料為
{4,9,12,7}的單連結串列。
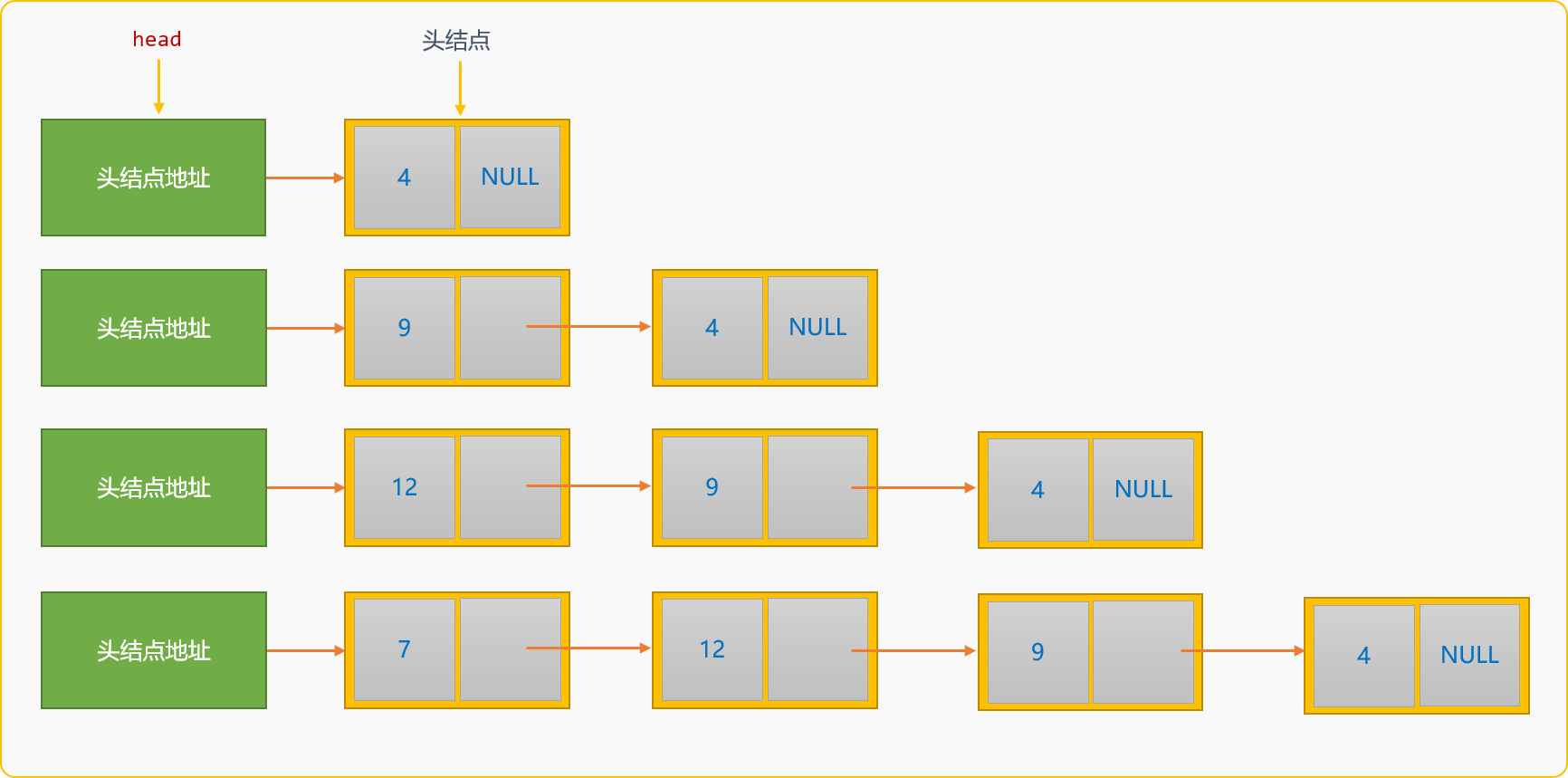
頭部插入建立單連結串列後,資料在連結串列中的儲存順序和資料的邏輯順序是相反的。如上圖所示。
注:上述插入演示沒有帶空白結點。
程式碼實現:
//頭部插入建立連結串列
void createFromHead(int n) {
LinkNode *newNode,*p;
p=this->head;
for(int i=0; i<n; i++) {
newNode=new LinkNode();
//輸入資料
cin>>newNode->data;
//原頭結點為新結點的後驅結點
newNode->next=p;
//新結點成為新的頭結點
p=newNode;
}
}
新增 3 個結點,測試上述建立的正確性。
LinkList list;
list.createFromHead(3);
LinkNode * head= list.getHead();
cout<<"輸出結點資訊"<<endl;
//顯示第一個結點
cout<<head->data<<endl;
//顯示第二個結點
cout<<head->next->data<<endl;
//顯示第三個結點
cout<<head->next->next->data<<endl;
執行結果:
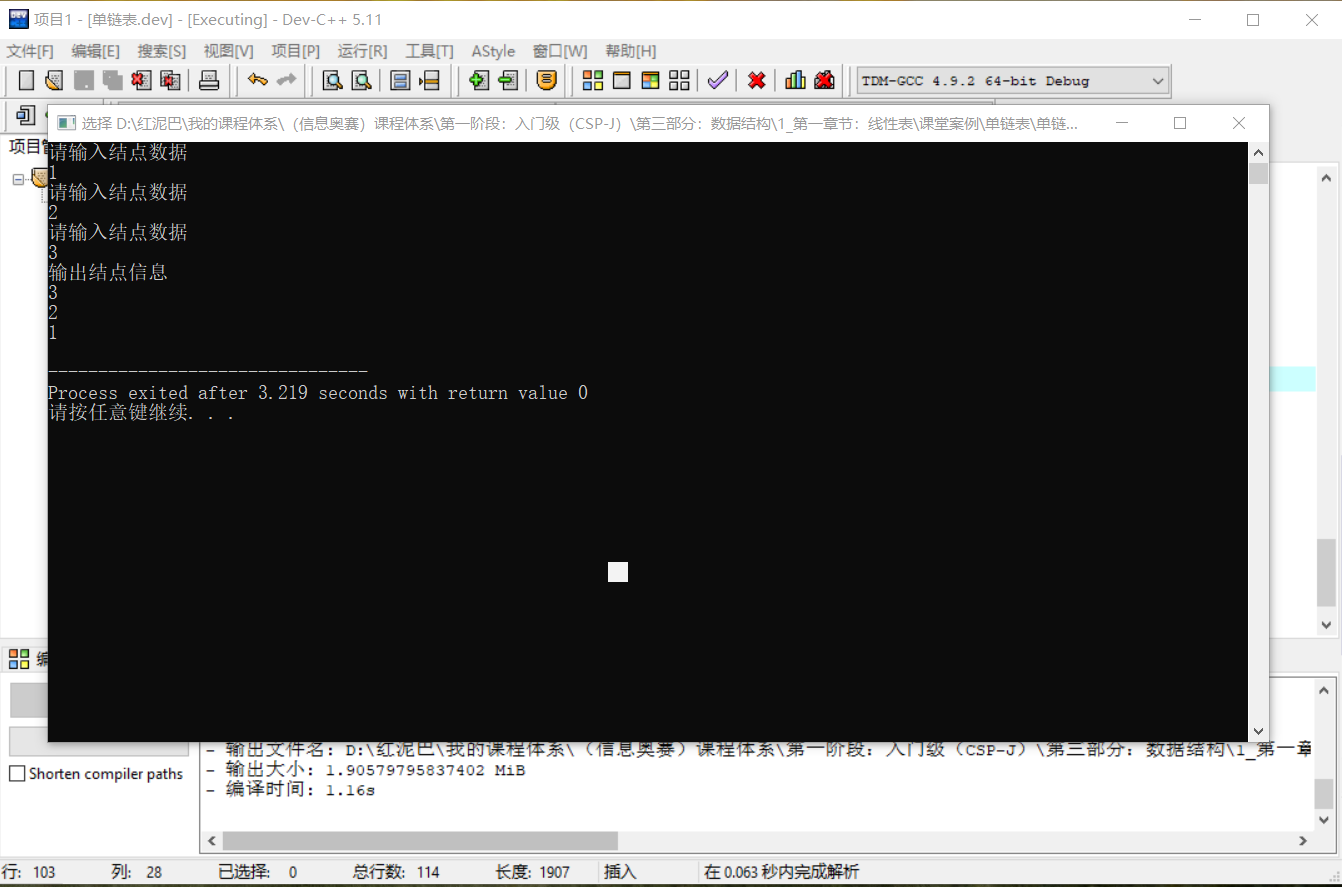
從結果可知,輸入順序和輸出順序是相反的。
- 尾部插入建立單連結串列,建立時的新結點替換原來的尾結點。如構建資料為
{4,9,12,7}的單連結串列。
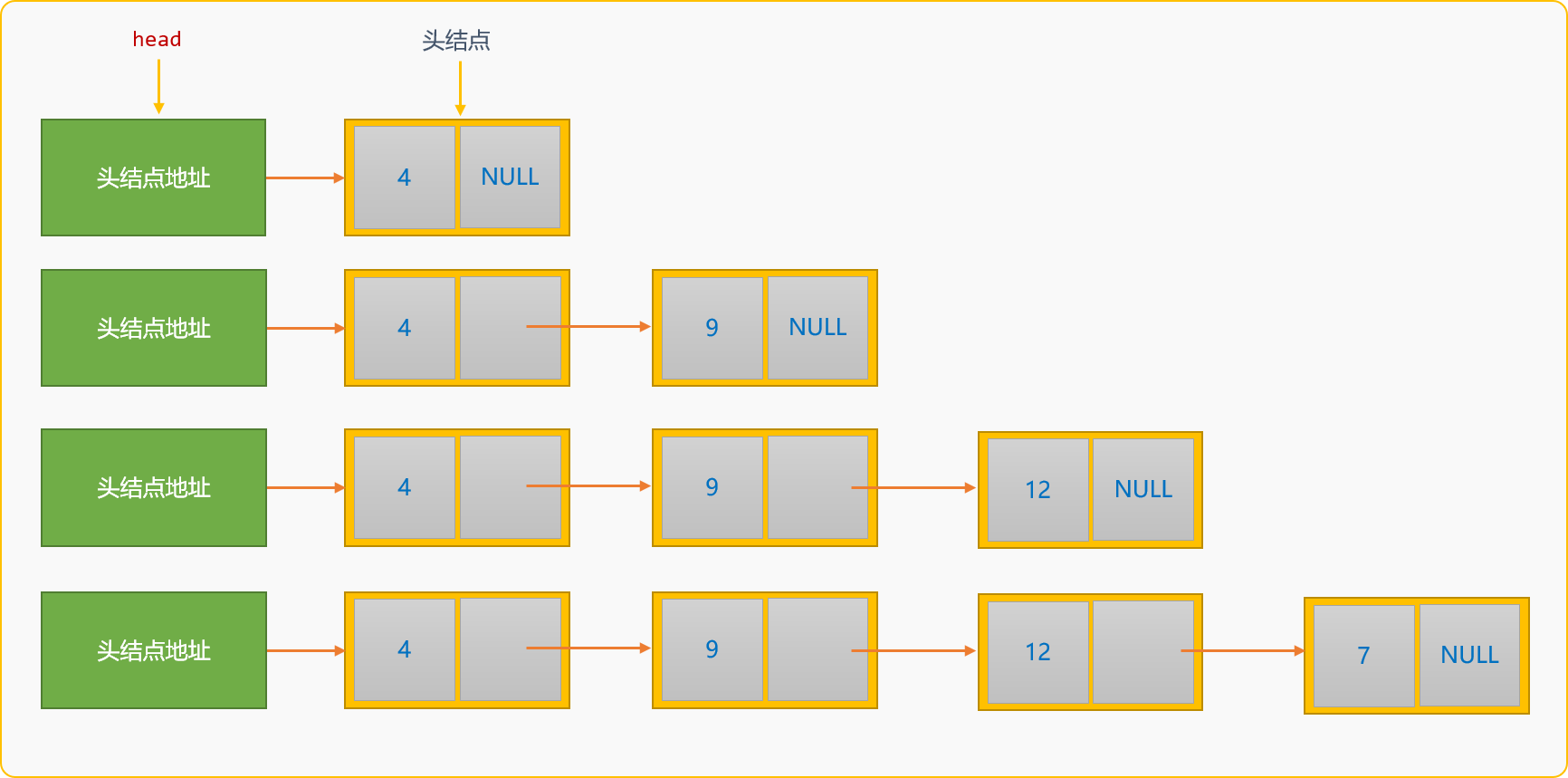
尾部插入方案建立的單連結串列,資料在連結串列中的儲存順序和資料的邏輯順序是一致,從而也能保證最終讀出來順序和輸入順序是一致的。
與頭部插入建立演演算法不同,除了需要儲存頭結點的地址資訊,尾部插入演演算法中還需要一個tail變數儲存尾結點的地址。初始時,tail和head指向同一個位置。
程式碼實現:
//從尾建連結串列
void createFromTail(int n) {
LinkNode *newNode,*p,*tail;
//頭結點地址
p=this->head;
//尾結點地址
tail=this->head;
for(int i=0; i<n; i++) {
//構建一個新結點
newNode=new LinkNode(0);
cout<<"請輸入結點資料"<<endl;
cin>>newNode->data;
if(p==NULL) {
//如果頭結點為 NULL
p=tail=newNode;
} else {
//原來的尾結點成為新結點的前驅結點
tail->next=newNode;
//新結點成為新的尾結點
tail=newNode;
}
}
this->head=p;
}
測試尾部插入建立的正確性:
int main(){
LinkList list {};
list.createFromTail(3);
LinkNode * head= list.getHead();
cout<<"輸出結點資訊"<<endl;
//顯示第一個結點
cout<<head->data<<endl;
//顯示第二個結點
cout<<head->next->data<<endl;
//顯示第三個結點
cout<<head->next->next->data<<endl;
}
執行後的結果:
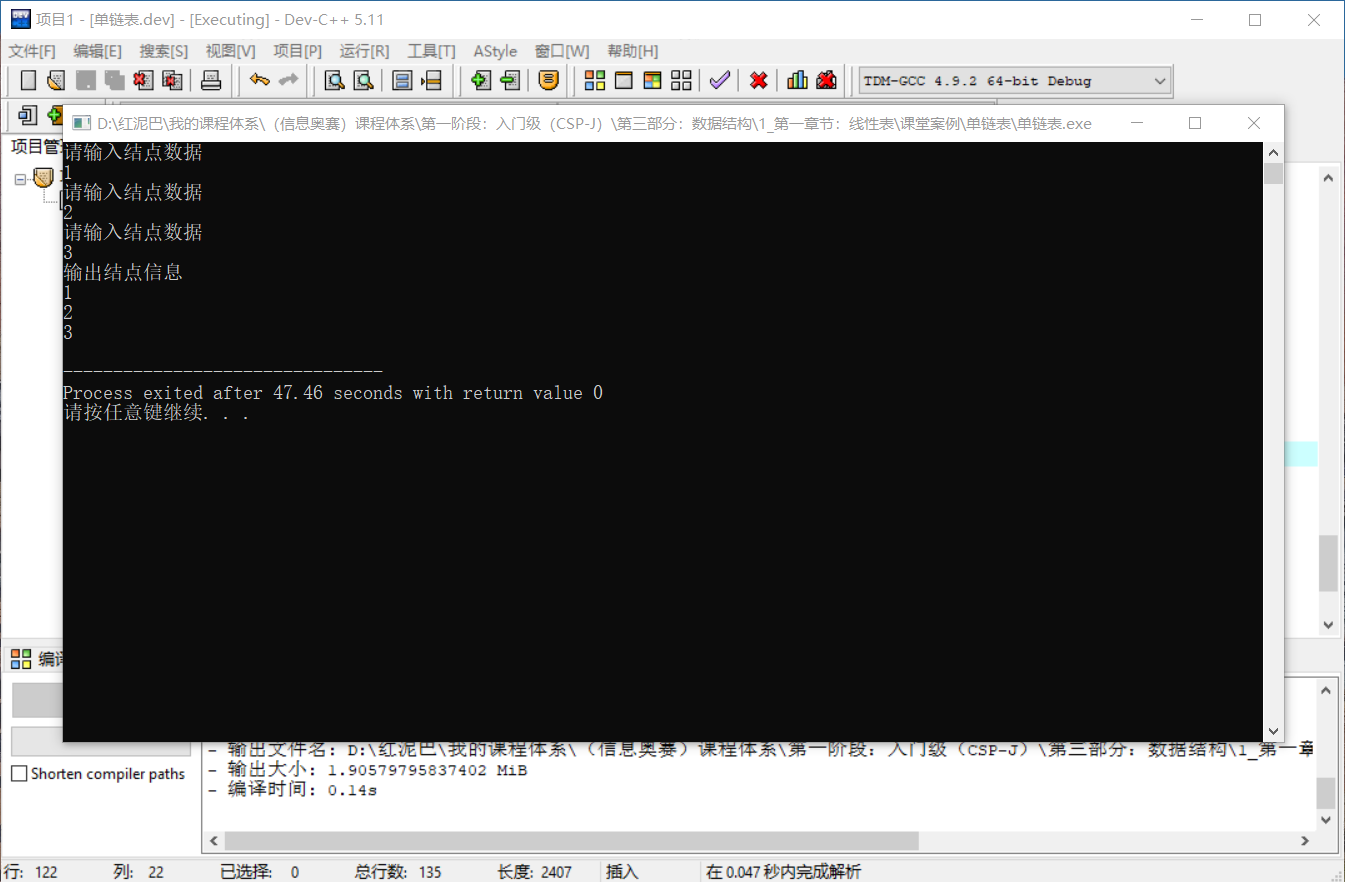
前文說過,初始化連結串列時,可以指定一個空白頭結點作為連結串列的頭結點。其意義在哪裡?
可以在尾部建立插入演演算法中使用或不使用空白頭結點了解一下程式碼的差異性 。上述尾部建立插入演演算法中,因連結串列是不帶空白結點的,所以在建立新結點時,必須有如下一段程式碼:
if(p==NULL) {
//如果頭結點為 NULL
p=tail=newNode;
}
因為剛開始時連結串列是空的,head和tail都是NULL,建立第一個新結點後,它即是頭結點,也是尾結點,所以head和tail都需要指向此新結點。
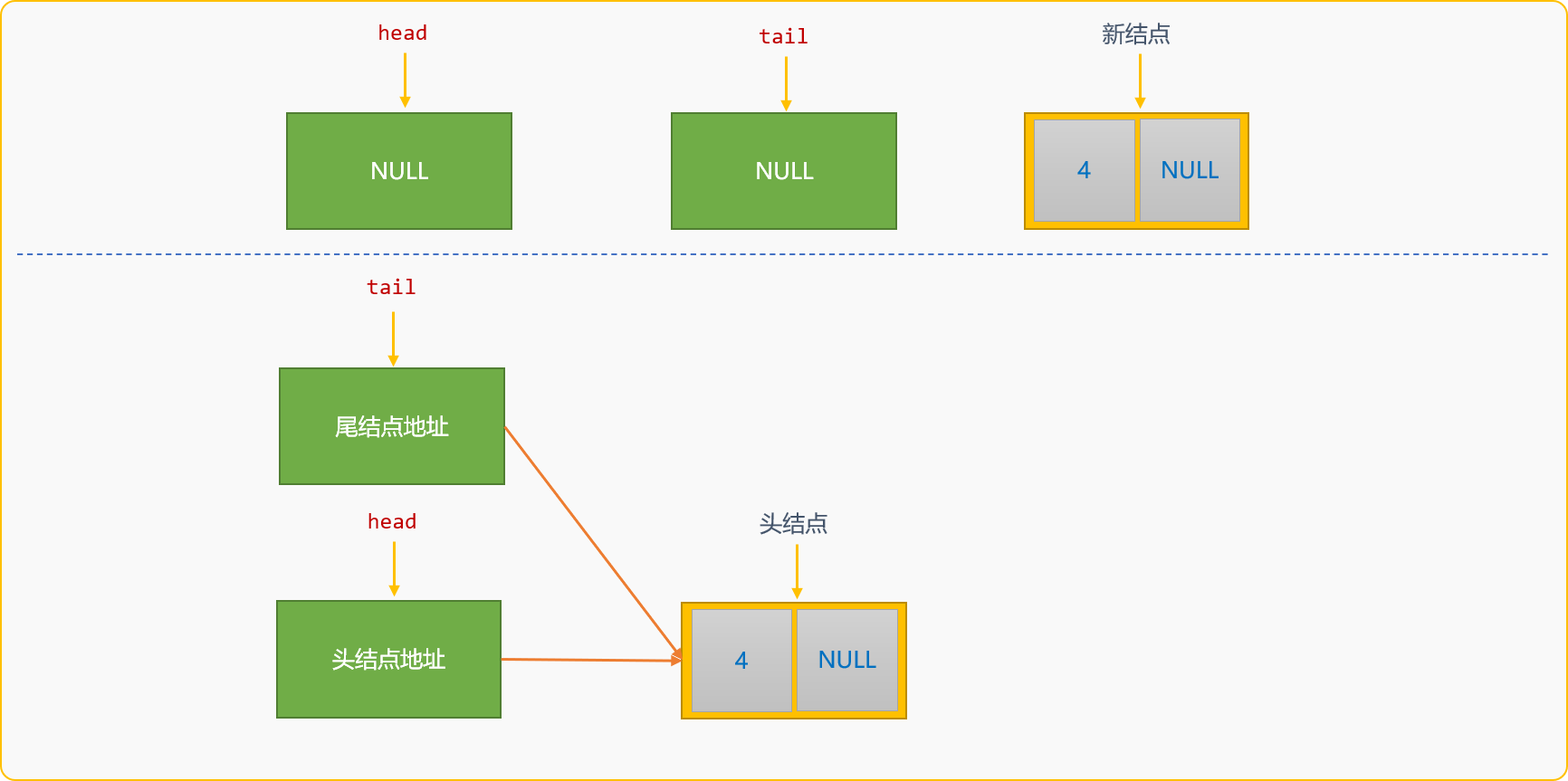
後續再建立新結點後,head則不需修改,通用邏輯是:原來的尾結點成為新結點的前驅結點,新建立的結點成為新的尾結點。
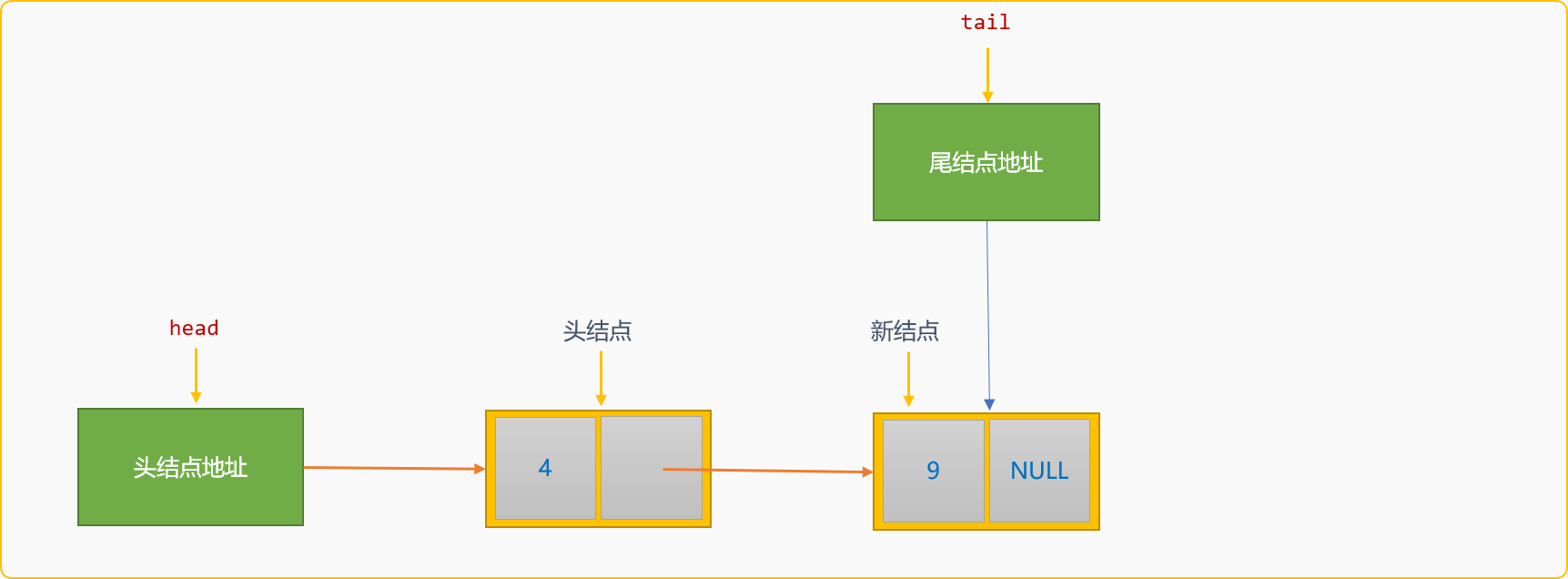
如果在初始化連結串列時,已經指定了一個空白結點,則尾部建立插入演演算法中只需遵循通用邏輯便可。
//初始化連結串列時指定一個空白結點作為頭結點
void initLinkList() {
this->head=new LinkNode(0);
}
尾部建立插入演演算法可修改為:
void createFromTail_(int n) {
LinkNode *newNode,*p,*tail;
//頭結點地址
p=this->head;
//尾結點地址
tail=p;
for(int i=0; i<n; i++) {
//構建一個新結點
newNode=new LinkNode(0);
cout<<"請輸入結點資料"<<endl;
cin>>newNode->data;
//原來的尾結點成為新結點的前驅結點
tail->next=newNode;
//新結點成為新的尾結點
tail=newNode;
}
this->head=p;
}
初始連結串列時如果指定了空白頭結點,就不需要考慮第一個結點的位置特殊性。
本文後續的演演算法都是基於帶空白頭結點的連結串列的操作。
2.3 查詢連結串列
連結串列中的常用查詢操作有 3 種方案:
- 按結點所在位置查詢。
- 按結點的值查詢。
- 查詢連結串列中的所有結點。
2.3.1 按結點位置查詢
設連結串列的頭結點為編號為 0的結點,當給定編號 i 後,從頭結點一至向後報數似的進行查詢,至到找到與給定i值相同的結點 。
//按位元置查詢結點
LinkNode * findNodeByIndex(int index) {
int j=0;
LinkNode *p=this->head;
if(index==j)
//如果 index 值為 0 ,返回頭結點
return p;
p=p->next;
while( p!=NULL && j<index) {
p=p->next;
j++;
}
if(j==index)return p;
else return NULL;
}
2.3.2 按結點的值查詢
掃描連結串列中的每一個結點,比較那一個結點的值和給定的引數值相同。
//按值查詢結點
LinkNode * findNodeByVal(dataType val) {
//如果不帶空白結點,則從頭結點開始查詢
LinkeNode *p=this->head;
whil(p!=null && p->data!=val ) {
p=p->next;
}
if(p!=NULL) {
return p;
} else {
return NULL;
}
}
如果連結串列帶有空白頭結點,可以從頭結點的後驅結點開始查詢。
LinkeNode *p=this->head->next;
因為是按值比較,所以,無論連結串列是否帶有空白頭結點,都可以從頭結點開始進行查詢,對結果沒有影響。
2.3.3 查詢所有
不帶空白頭結點遍歷操作:
//顯示所有
void showSelf() {
if(this->head==NULL)return;
LinkNode *p=this->head;
while(p!=NULL) {
cout<<p->data<<"\t";
p=p->next;
}
}
帶空白頭結點的遍歷:
//顯示所有
void showSelf() {
if(this->head==NULL)return;
LinkNode *p=this->head->next;
while(p!=NULL) {
cout<<p->data<<"\t";
p=p->next;
}
}
2.4 插入
連結串列建立好後,後續維護過程,難免時時需要插入新的結點。插入時可以如前文在建立連結串列時一樣,在頭部插入和尾部插入。這裡的插入指在連結串列的某個中間位置插入新結點。
- 後插入。
- 前插入。
2.4.1 後插入
所謂後插入,指新結點插入到某個已知結點的後面。如下圖所示:
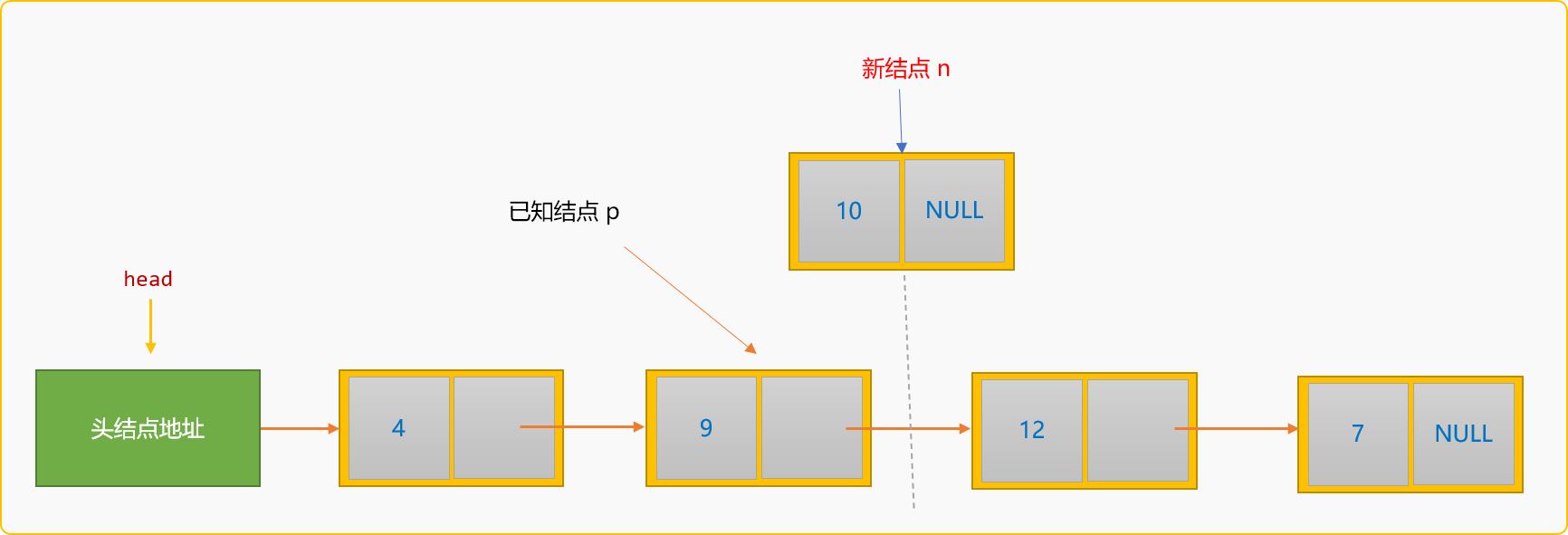
如果把值為 10 的新結點插入到值為 9的結點之後,稱為後插入。後插入的通用邏輯:
-
查詢到值為
9的結點地址,稱為p結點。 -
建立新結點。
-
指定新結點
n的後驅結點為p的後驅結點。n->next=p->next;
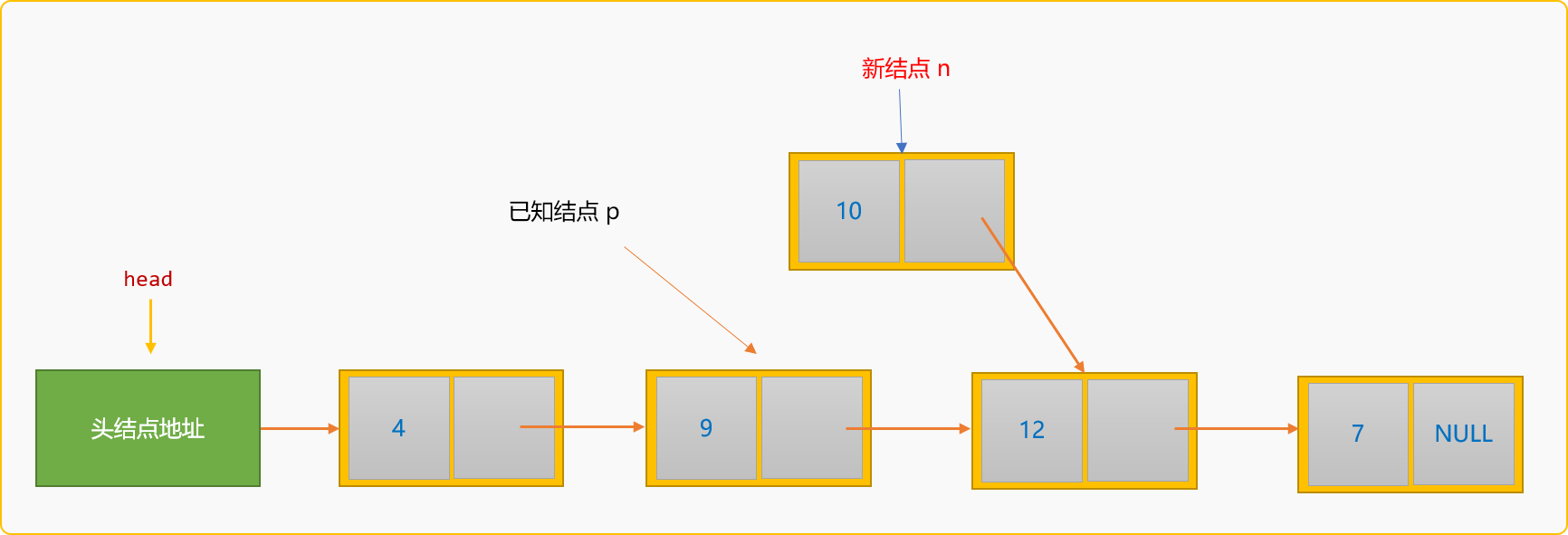
-
指定
p的後驅結點為新結點n。p->next=n;
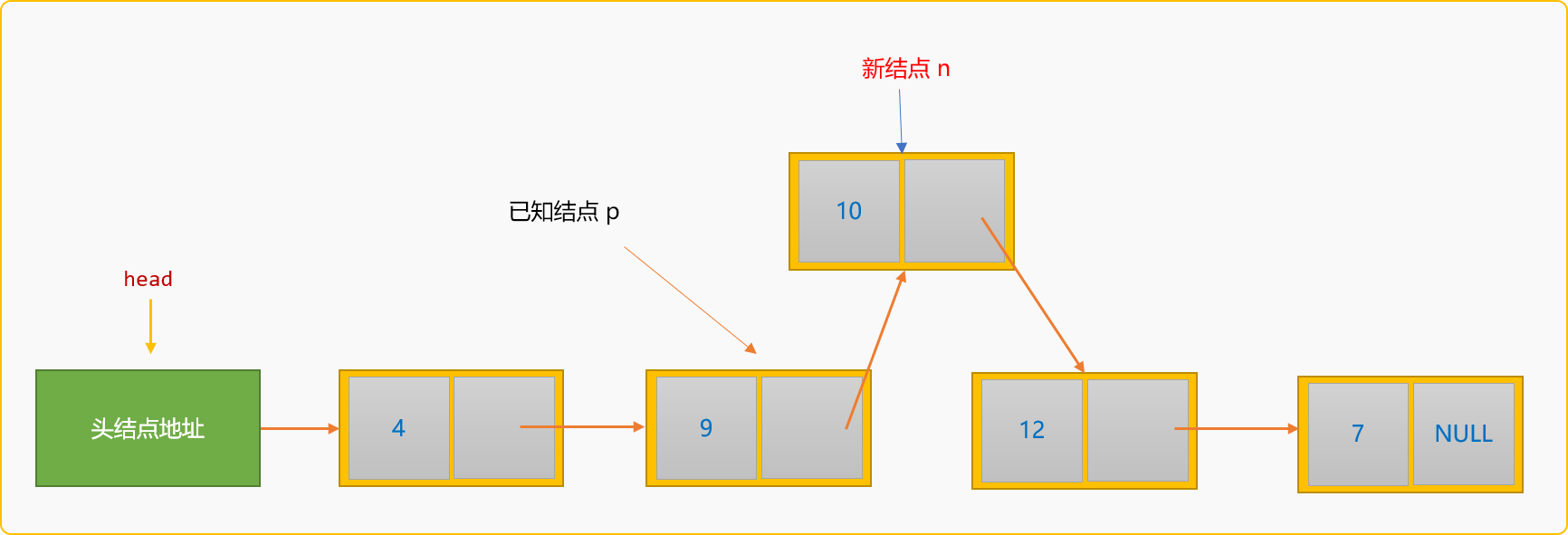
程式碼實現:
//後插入
int instertAfter(dataType val,dataType data) {
//按值查詢到結點
LinkNode *p=this->findNodeByVal(val);
if (p==NULL){
return false;
}
LinkNode *n=new LinkNode(0);
n->data=data;
n->next=p->next;
p->next=n;
return true;
}
測試後插入操作:
int main(int argc, char** argv) {
LinkList list {};
//建立值為 1 ,2 ,3 的 3 個結點
list.createFromTail(3);
//在值為 2 的結點後面插入一個值為5 的新結點
list.instertAfter(2,5);
//在連結串列中檢視是否存在值為 5 的結點
list.showSelf();
return 0;
}
執行後輸出結果:
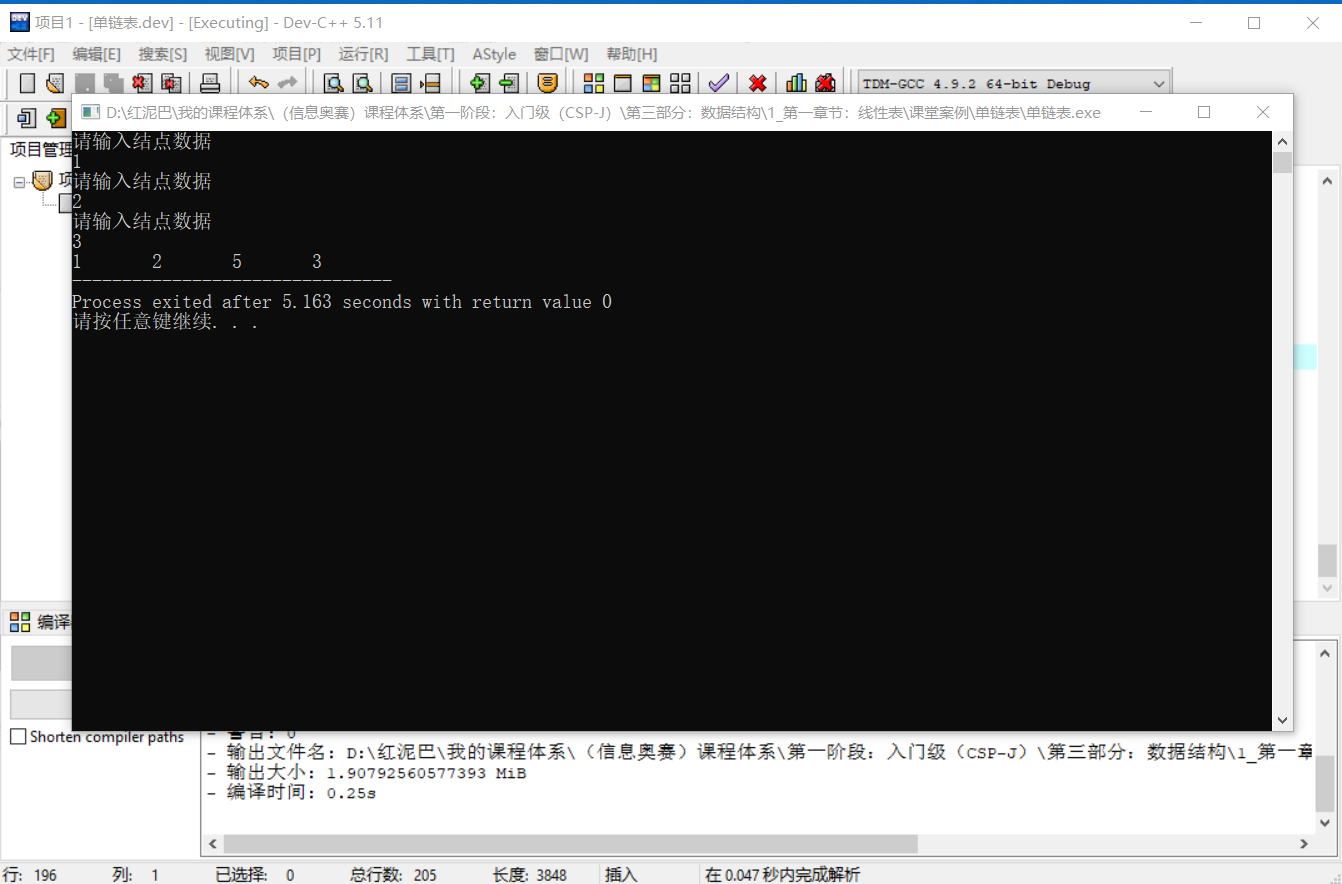
2.4.2 前插入
所謂前插入,指新結點插入到某個已知結點的前面。如下圖所示:
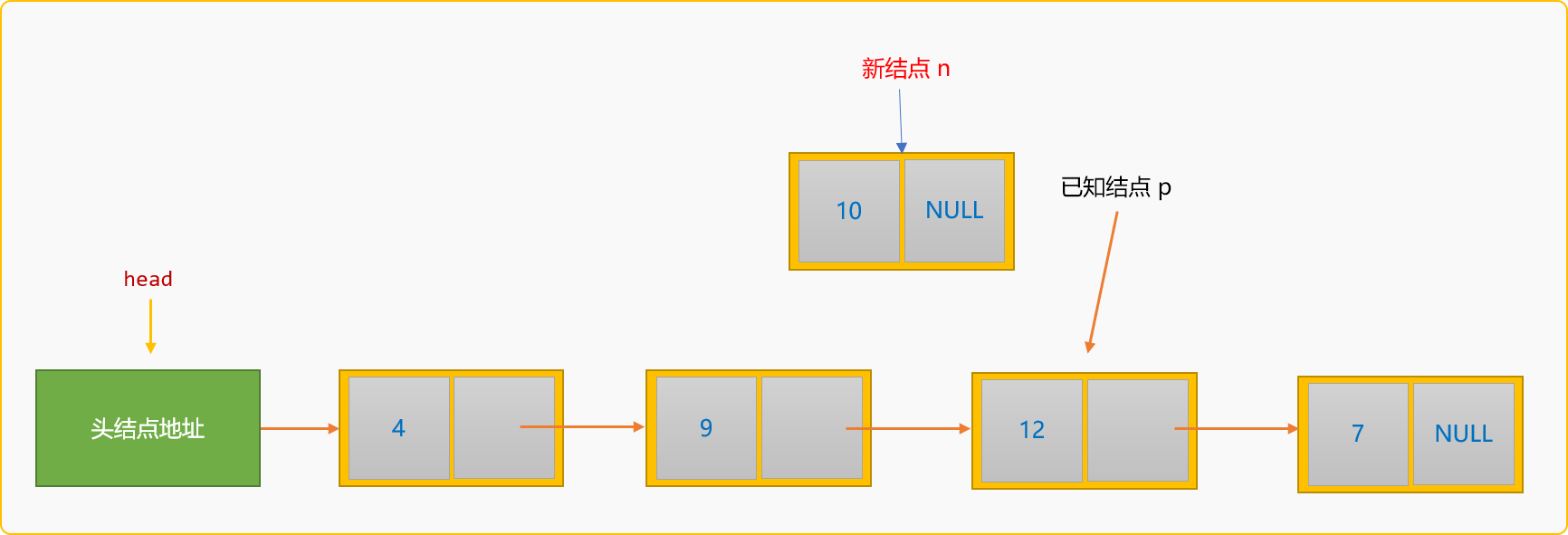
如果把新結點n插入到已知結點p的前面,則稱為前插入。前插入的通用邏輯:
- 除了要查詢到
p結點在連結串列中的地址,還需要知道p結點的前驅結點p1的地址。
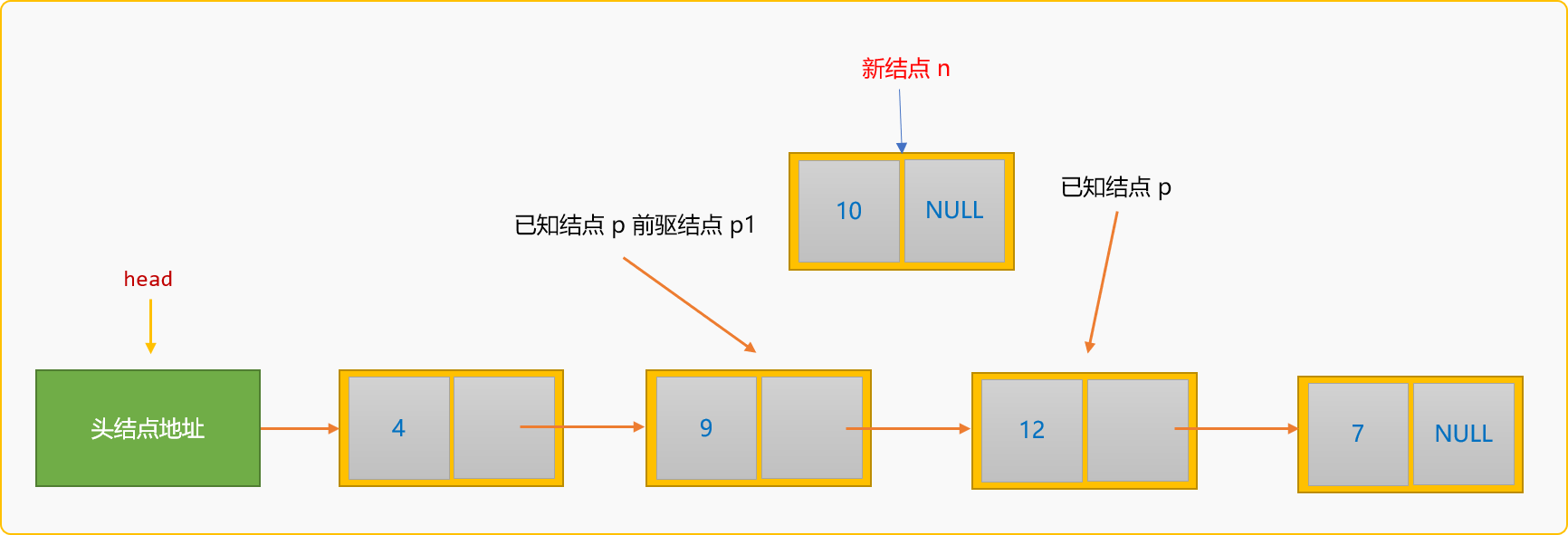
- 建立新結點,然後指定新結點
n的後驅結點為p結點。
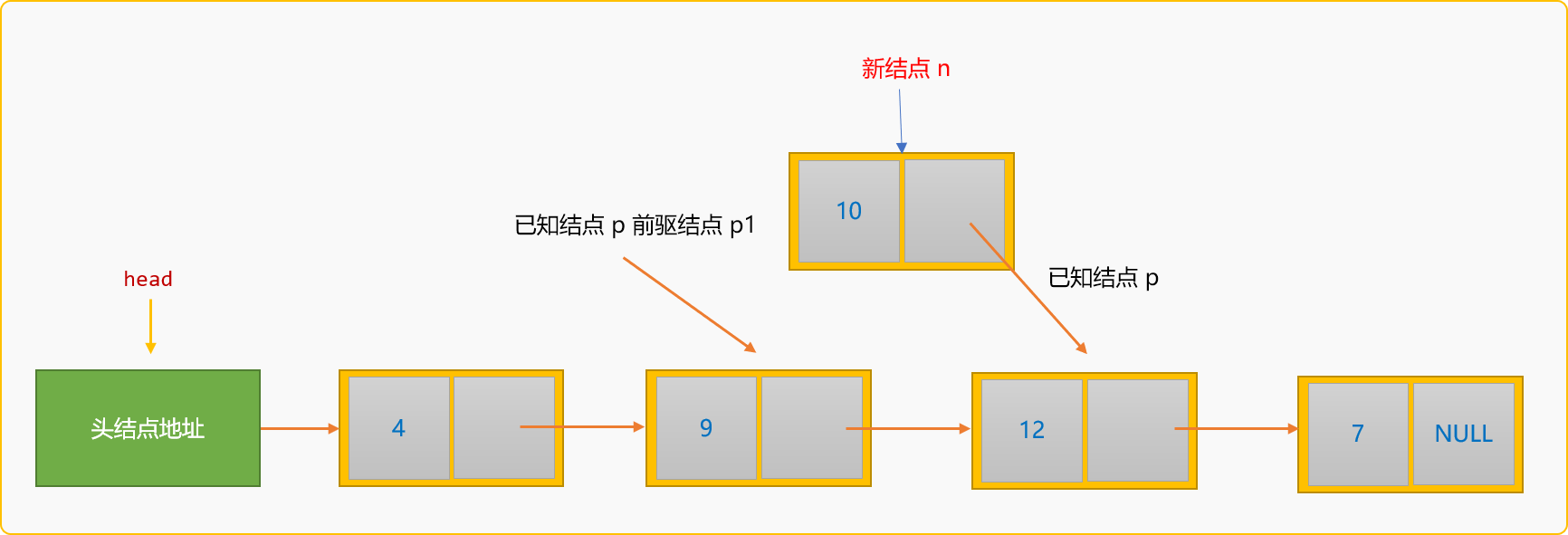
- 指定結點
p1的後驅結點為新結點n。
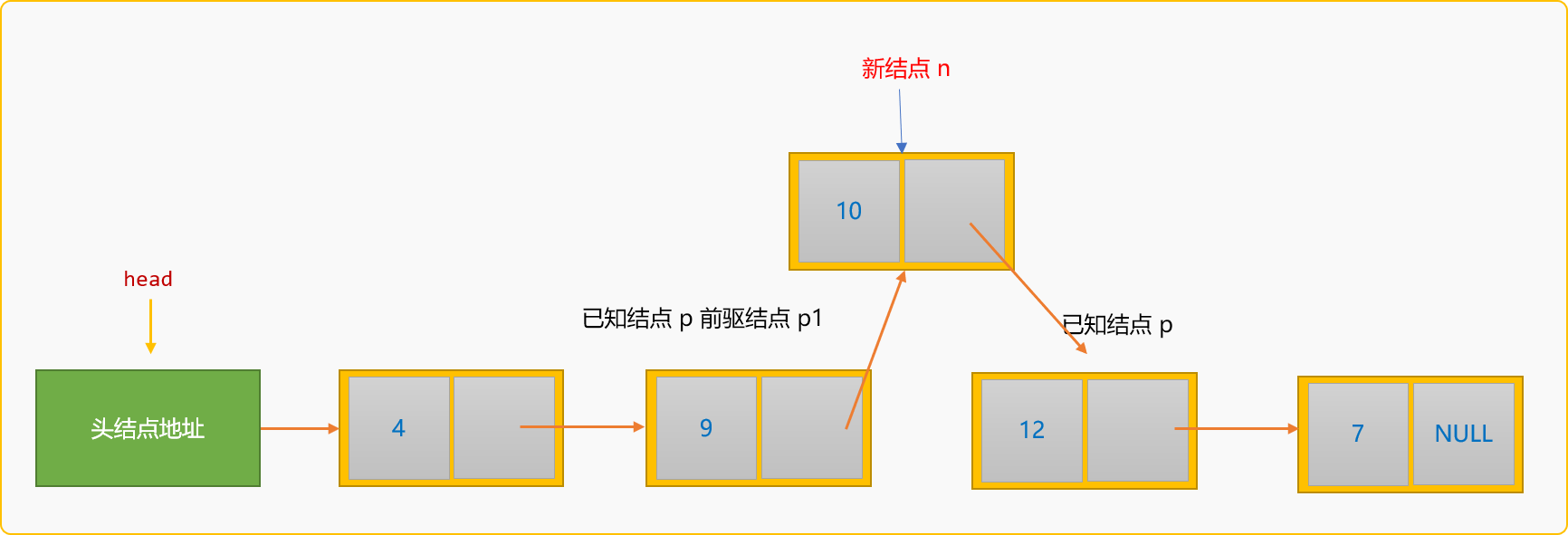
程式碼實現:
/前插入
int insertBefore(dataType val,dataType data) {
//按值查詢到結點
LinkNode *p=this->findNodeByVal(val);
//查詢前驅結點
LinkNode *p1=this->head;
while(p1->next!=p){
p1=p1->next;
}
//構建新結點
LinkNode *n=new LinkeNode(0);
n->data=data;
//新結的點的後驅為 p 結點
n->next=p;
//重設 p1 的後驅為 n
p1->next=n;
}
測試前插入操作:
int main(int argc, char** argv) {
LinkList list {};
//建立值為 1 ,2 ,3 的 3 個結點
list.createFromTail(3);
//在值為 2 的結點前面插入一個值為5 的新結點
list.insertBefore(2,5);
//在連結串列中檢視是否存在值為 5 的結點
list.showSelf();
return 0;
}
執行後輸出結果:
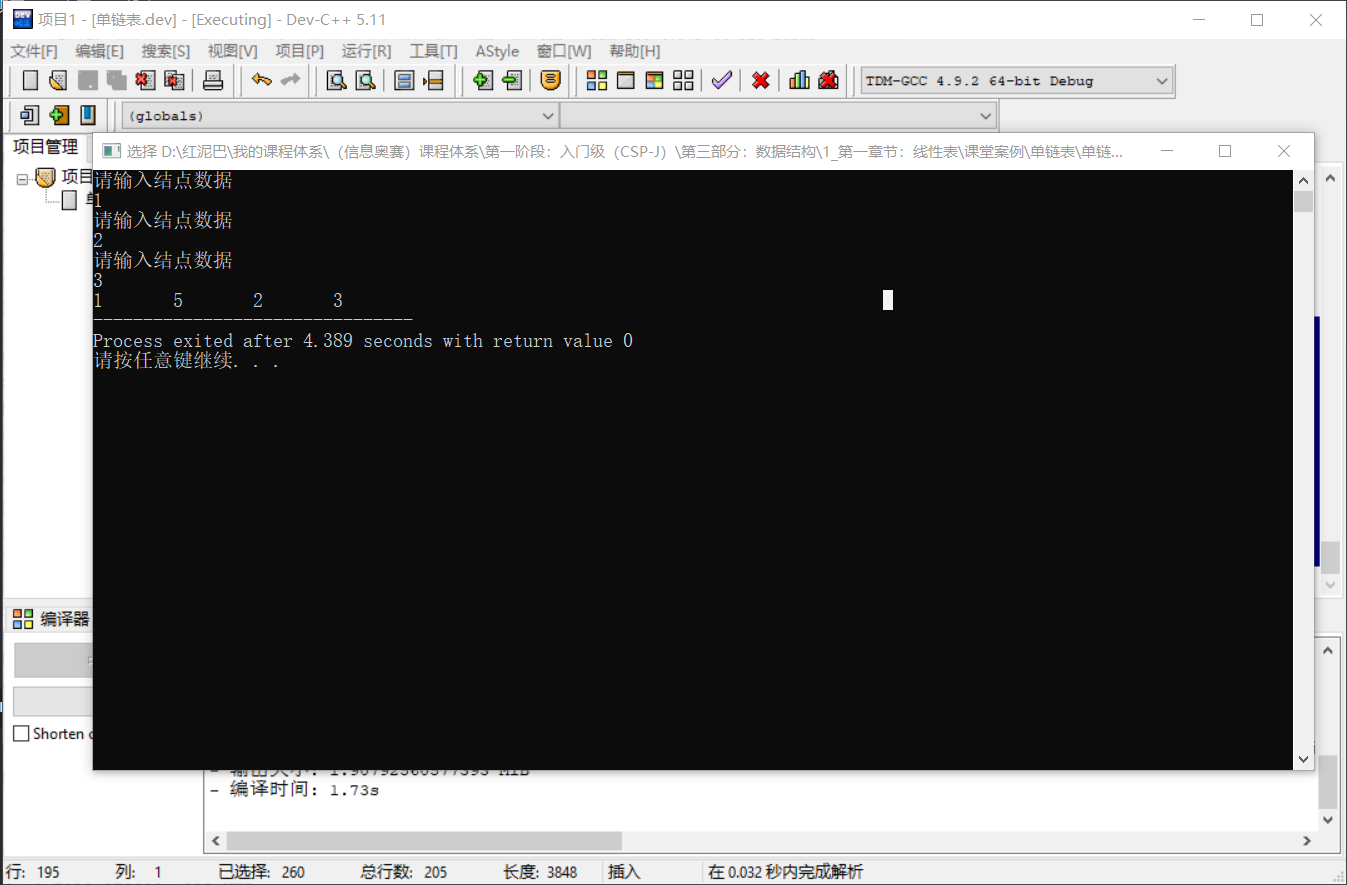
如果僅僅是關心資料在連結串列中的邏輯關係,則可以先把新結點n插入到結點p的後面,然後交換 2 個結點中的資料。
2.5 刪除
刪除演演算法包括:
- 刪除某一個結點。
- 刪除所有結點,也稱為清空連結串列。
2.5.1 刪除結點
刪除結點的基本思路:
- 在連結串列中查詢到要刪除的結點
p。

- 找到
p結點的前驅結點p1。

-
指定
p1的後驅結點為p的後驅結點。p1->next=p->next;
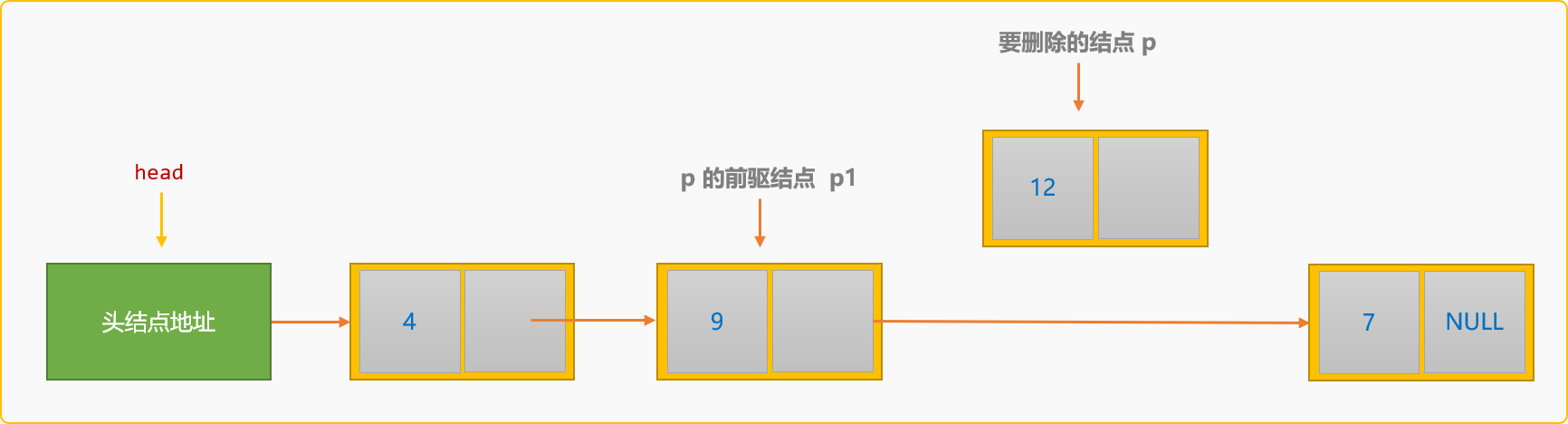
編碼實現:
//按值刪除結點
int delNode(dataType data) {
//按值查詢到要刪除的結點
LinkNode *p= this->findNodeByVal(data);
if (p==NULL)return false;
//查詢前驅結點
LinkNode *p1=this->head;
while(p1->next!=p)p1=p1->next;
//刪除操作
p1->next=p->next;
p->next=NULL;
delete p;
return true;
}
測試刪除操作:
int main(int argc, char** argv) {
LinkList list {};
//建立值為 1 ,2 ,3 的 3 個結點
list.createFromTail(3);
//刪除值為 2 的結點
list.delNode(2);
list.showSelf();
return 0;
}
輸出結果:
2.5.2 清空連結串列
清空連結串列指刪除所有結點。從頭結點開始掃描,找到一個刪除一個,真到沒有結點為止。
void delAll() {
LinkNode *p=this->head;
//臨時結點
LinkNode *p1;
while(p!=NULL) {
//保留刪除結點的後驅結點
q=p->next;
delete p;
p=q;
}
this->head=NULL;
}
測試:
int main(int argc, char** argv) {
LinkList list {};
//建立值為 1 ,2 ,3 的 3 個結點
list.createFromTail(3);
//沒刪除之前
cout<<"清除之前:"<<endl;
list.showSelf();
//清除連結串列
list.delAll();
//顯示
cout<<endl<<"清除之後:"<<endl;
list.showSelf();
return 0;
}
輸出結果:
2.6 時間複雜度分析
在連結串列中查詢的時間複雜為 O(n)。
在連結串列中進行插入操作時,先要查詢到結點,如果不計查詢時間,僅從插入演演算法本身而言,後插入演演算法時間複雜度為O(1)。因前插入演演算法需要要查詢前驅結點,時間複雜度為O(n)。
刪除結點時同樣需要查詢到被刪除結點的前驅結點,時間複雜度為O(n),如果是刪除某個結點的後驅結點,時間複雜度為O(1)。
通過上述的基本操作得知:
- 單連結串列上插入、刪除一個結點,需要知道其前驅結點的地址。
- 單連結串列不具有按序號隨機存取的特點,只能從頭結點開始依次查詢。
3. 總結
本文主要講解單連結串列的概念以及基於單連結串列的基本操作演演算法,除了單連結串列,還有迴圈連結串列、雙向連結串列,將在後繼博文中再詳細討論。無論連結串列的結構如何變化,單連結串列都是這種變化的始端。