【深度學習】——深度學習中的梯度計算
梯度下降在【機器學習基礎】中已經總結了,而在深度學習中,由於模型更加複雜,梯度的求解難度更大,這裡對在深度學習中的梯度計算方法進行回顧和學習。
本節主要是瞭解深度學習中(或者說是tensorflow中)梯度的計算是怎麼做的。
1. 計算圖
在學習tensorflow中,我們知道tensorflow都是基於圖來進行計算的,那麼什麼是計算圖呢?
所謂計算圖就是將一個function利用圖的結構來進行表示。如圖所示:
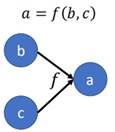
上面的圖就表示a=f(b,c)這樣一個方程,而圖的節點表示變數,圖的邊表示操作(operation)。
再比如方程f=f(g(h(x)))這樣一個方程,用計算圖來表示:
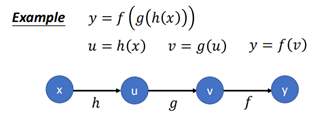
之所以用計算圖來表示方程,是因為圖能夠使得方程的結構更加清晰,計算順序上一目瞭然,同時為後面的梯度提供了很大的便利性。接著往後看。
有了計算圖,根據一個計算式,我們就可以構建出一張圖出來,比如:
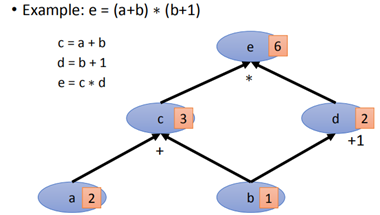
根據所建立的圖,給定a=2,b=1,則可以順著圖結構順利求出e。
2. 計算圖的鏈式求導法則
例子1:函數z=h(g(x)),按照上面的做法,將其變成計算圖如圖所示:
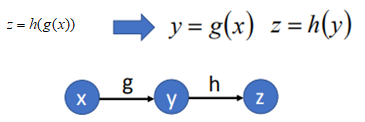
根據鏈式求導求dz/dx,z先對y求導,然後y再對x求導得到:
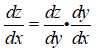
例子2:另一個更復雜的z=k(g(s), h(s))這樣一個函數,求dz/ds,首先建立一張計算圖:
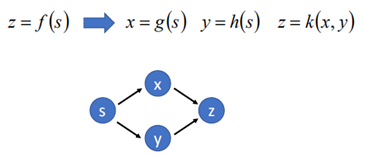
根據鏈式求導法則,s和x、y均有關係,因此z對x求導,x再對s求導是一條路,然後z對y求導,y再對s求導另一條路,兩條路相加得到:
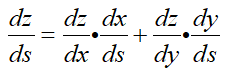
上面就是鏈式求導法則,那麼鏈式求導法則在圖計算中如何應用呢,繼續使用上面那個e=(a+b)*(b+1):
根據我們建立的計算圖和鏈式求導法則,求de/db:
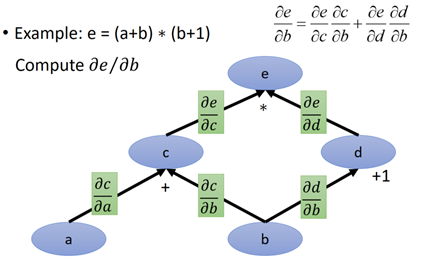
然後分別對每個邊的導數進行計算:
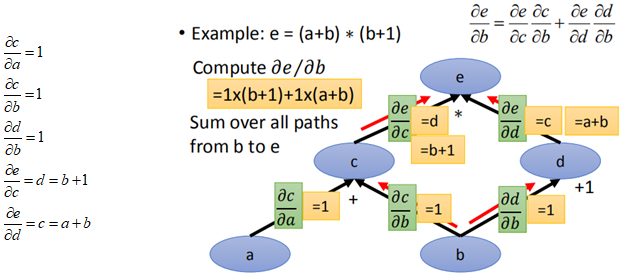
那麼假如a=3,b=2,求e對b的導數,a、b代進上面的每條邊上,將所要求的導數記為1,從1開始出發:
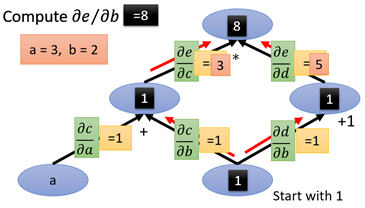
那麼最後沿著紅色的箭頭一路計算b到e的路徑就可以了(這裡可以不用管節點的值):
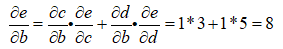
從這裡可以看到,圖計算在求導數的計算中非常便利且清晰。
那麼這麼對於梯度的求解有什麼好處呢?我們可以用reverse mode,利用圖計算,從頂端開始,向底部走:
還是如果求e對b的導數,這次從e開始走,e=1,然後向下走能夠到達b的每一條路:
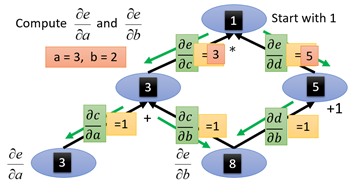
也就是圖中綠色的箭頭的方向,即為reverse mode。需要求e對a的導數,則就從e一路走到a就可以了
這裡注意,反向的路徑箭頭必須是反向的,也就是隻能沿著綠色的箭頭能夠到達a的路徑,因此從e到a只有一條路:
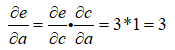
下面再舉一個例子:
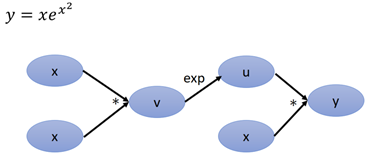
建立計算圖後,然後為每個邊補上對應的導數,這裡需要注意,v=x2,那v對x的導數應該是2x,但是這裡x*x相當於是兩個變數,要區分對待,當做x1、x2:
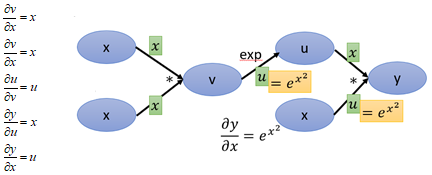
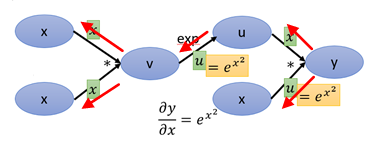
接下來求y對x的導數,沿著紅色的箭頭,一共有3條路徑:
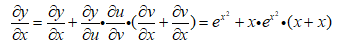
3. 深度學習中的梯度計算
有了上面的計算圖和反向求導,以及幾個範例的說明,對於深度學習中的梯度計算就有了一個初步的雛形了。不過是在深度學習中的方程更加複雜而已。
我們只需要能夠畫出深度學習中的計算圖,那麼計算梯度也就水到渠成。
3.1 全連線網路的梯度計算
首先來看全連線神經網路,在【機器學習基礎】中對反向傳播的過程進行了描述,分為前向和後向兩個方面:
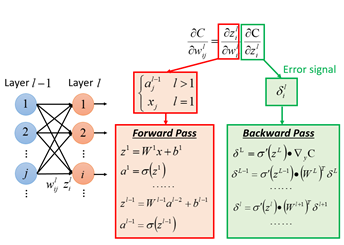
紅色框中的正向傳播用於求z對w的導數,綠色框的反向傳播用於求loss對z的導數,二者相乘最終得到loss對w的導數。
而反向傳播像是從loss開始,向輸出層傳遞的一種「正向傳播」過程:
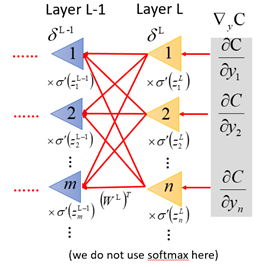
根據全連線網路的正向傳播過程,整個網路的從輸入到輸出的方程為:
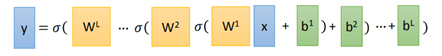
於是,按照上面這個方程,全連線網路的計算圖表示如下(假設只有2個隱藏層):
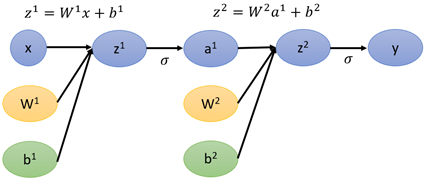
最終得到的y與真實的yhat計算loss,那麼按照上面計算圖以及導數計算的方法,則有:
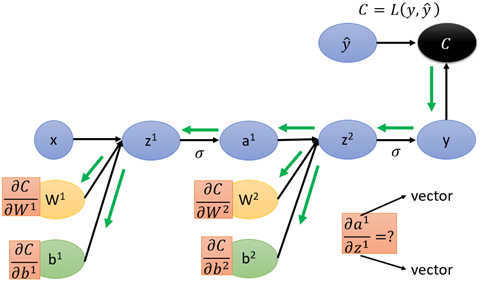
在計算每一部分導數之前,由於網路的輸入和中間變數均為矩陣,這裡需要了解Jacobian Matrix(雅克比矩陣):
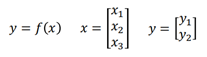
y是2*1的矩陣,x是3*1的矩陣,那麼y對x的導數:
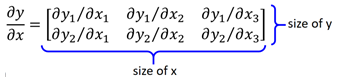
行數是y原來的size,列數為原來x的size。比如:
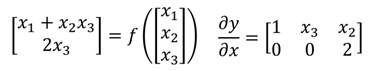
接下來回到全連線的計算圖的梯度計算,使用reverse mode,從後向前一部分一部分來看:
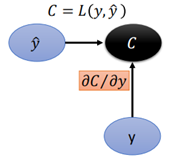
首先是loss C對y的導數,在計算loss時,採用cross entropy:
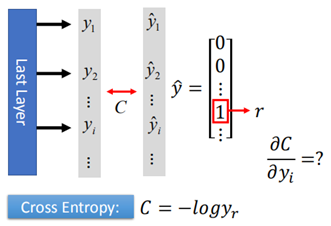
C是一個數,y是一個m*1矩陣(m表示類別數量),那麼根據Jacobian Matrix 知道C對y的導數為1*m。
假設樣本屬於第r類,那麼第r維=1,其他為0,因此用矩陣的形式計算:
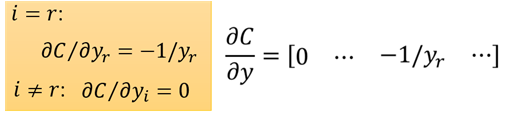
接下來看下一層:
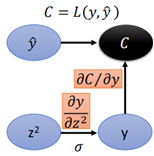
y對z2的導數,首先可以確定y對z2導數的形狀,y為10*1,z2經過σ啟用函數,形狀不變,一次z2也是10*1的矩陣,那麼y對z2的導數為一個方形;
而y=σ(z2),那麼根據Jacobian Matrix,當yi是由zi求出來的元素才有值,其他y不是由z計算得來的那些都為0(因為二者根本沒有關係)。
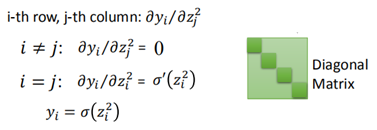
因此y對z2的導數是一個方形的對角矩陣。
然後繼續到下一層:
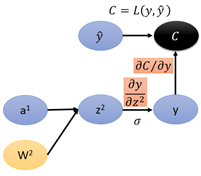
z1是由w2和a1得到的:
首先看z2對a1的導數,a1是前一層的輸出,那麼有:
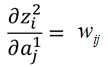
因此,z2對a1的導數就是W2。
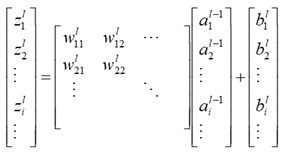
然後是z2對W2的導數,z2是1*m的矩陣,W2是一個m*n的矩陣(n為上一層的輸出維度),那麼導數就是這樣的:
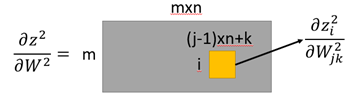
這個可以理解為矩陣中元素依舊是矩陣的形式,而其中當i=j時,z2(i)對w2(j)的導數為a1,i≠j時,z2i與w2j沒有關係, 到時為0。於是:
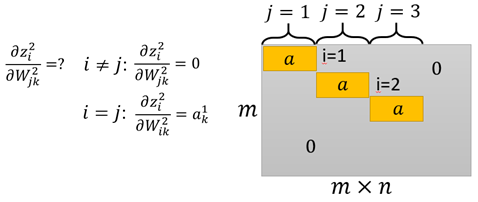
網路再繼續往前,跟上述的過程基本一致,那麼最後得到計算圖的每一邊上的導數:
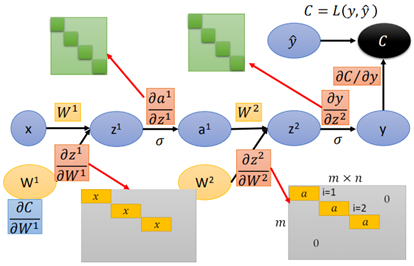
那麼此時可以求loss對任意引數的導數:
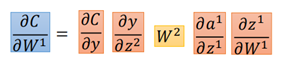
3.2 RNN中的梯度計算
RNN的梯度計算也一樣是根據計算圖來一步一步地對每一部分求導,然後再用reverse mode計算loss對各個引數的導數。RNN的基本結構如下:
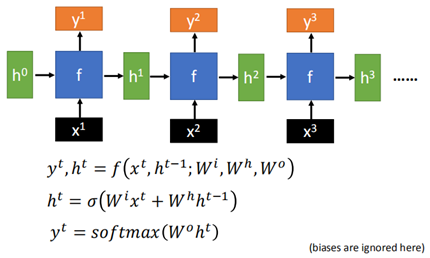
對於每一部分,按照計算圖的形式,正常的計算圖應該是這樣的:
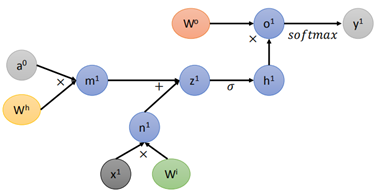
為方便計算和圖的簡潔性,將上圖改為下面這樣:
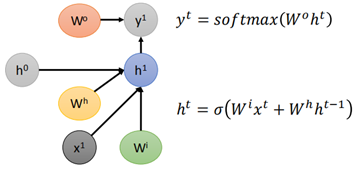
那麼對於整個RNN網路的結構的計算圖:
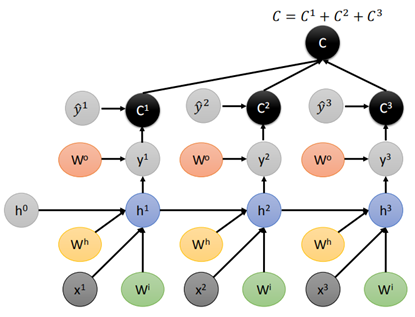
每一個時刻都要計算一個loss C,然後對於一個樣本,要將所有時刻的C相加得到最終的loss。
有了計算圖,然後計算每個邊上的導數:
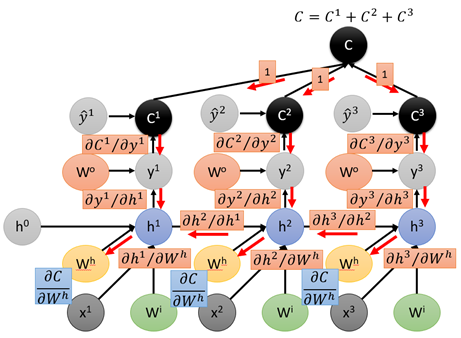
這裡對於每條邊的具體計算過程就不再展開了,接下來就可以求C對wh和C對wi的導數了:
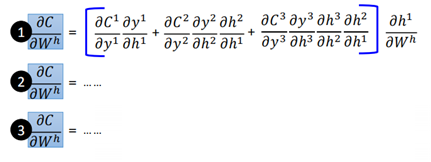
這裡需要注意的是,wh有3個,因此也是由三部分相加,而對於每一個wh,又有可能有多條路徑,如①號wh,一共有三條路徑:
C→C1→y1→h1→wh
C→C2→y2→h2→h1→wh
C→C3→y3→h3→h2→h1→wh
②號wh只有兩條路徑,③號wh有一條路徑。注意這裡的路徑都是隻能沿著紅色箭頭的方向行進到達wh的路徑。
最終得到三部分wh的導數,然後進行相加:

這樣就完成了RNN的梯度的計算。在tensorflow中就是這麼運作的。
參考資料:
李宏毅《深度學習-Computing Graph》
這一部分就介紹了這麼多,主要了解在深度學習中以矩陣運算的形式如何進行的。