分類問題

分類問題是人工智慧領域中最常見的一類問題之一，掌握合適的評價指標，對模型進行恰當的評價，是至關重要的。

同樣地，分割問題是畫素級別的分類，除了mAcc、mIoU之外，也可以採用分類問題的一些指標來評價。

本文對分類問題的常見評價指標進行介紹，並附上利用sklearn庫的python實現。

將從以下三個方面分別介紹：

常用評價指標
混淆矩陣繪製及評價指標計算
ROC曲線繪製及AUC計算

1. 常用評價指標

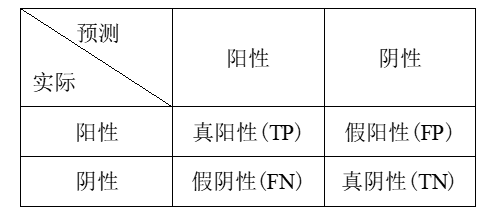
混淆矩陣（confusion matrix）

一般用來描述一個分類器分類的準確程度。
根據分類器在測試資料集上的預測是否正確可以分為四種情況：

TP(True Positive)——將正類預測為正類數；
FN(False Negative)——將正類預測為負類數；
FP(False Positive)——將負類預測為正類數；
TN(True Negative)——將負類預測為負類數。
構成一個二分類的混淆矩陣如圖：

均交併比（Mean Intersection over Union，mIoU)：

為語意分割的標準度量。其計算兩個集合的交併比，在語意分割的問題中，這兩個集合為真實值（ground truth）和預測值（predicted segmentation）。

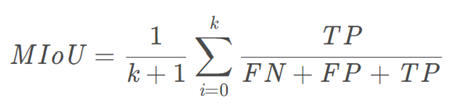
分類問題評價指標

二分類問題經混淆矩陣的處理後，針對不同問題，可以選用不同的指標來評價系統。

Accuracy：表示預測結果的精確度，預測正確的樣本數除以總樣本數；
Precision：準確率，表示預測結果中，預測為正樣本的樣本中，正確預測為正樣本的概率；
Sensitivity：靈敏度，表示在原始樣本的正樣本中，最後被正確預測為正樣本的概率；
Specificity：常常稱作特異性，它研究的樣本集是原始樣本中的負樣本，表示的是在這些負樣本中最後被正確預測為負樣本的概率；
F1-score：表示的是precision和recall的調和平均評估指標。

受試者工作特徵（Receiver Operating Characteristic，ROC）曲線

ROC曲線是以真陽性率（TPR）為Y軸，以假陽性率（FPR）為X軸做的圖。同樣用來綜合評價模型分類情況。是反映敏感性和特異性連續變數的綜合指標。

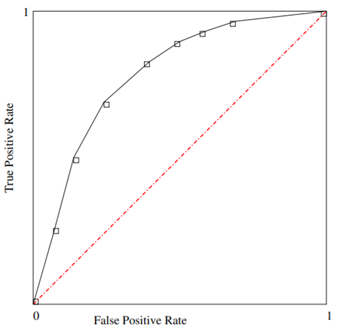
AUC（Area Under Curve）

AUC的值為ROC曲線下與x軸圍成的面積，分類器的效能越接近完美，AUC的值越接近。當0.5>AUC>1時，效果優於「隨機猜測」。一般情況下，模型的AUC值應當在此範圍內。

2. 混淆矩陣繪製及評價指標計算

首先是分類器的訓練，以sklearn庫中的基礎分類器為例

import numpy as np
import pandas as pd
from sklearn.svm import SVC, LinearSVC
from sklearn import metrics
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt


clf = LinearSVC()
clf.fit(train_features, train_target)
predict = clf.predict(test_features)

# 繪製混淆矩陣和評價指標計算
cal(test_target, pred)

# 獲取分類score
score = clf.decision_function(test_features)

# 繪製ROC曲線和計算AUC
paint_ROC(test_target, test_score)

混淆矩陣的繪製和評價指標計算可以寫在一起，在繪製混淆矩陣時，已經可以算出TP\TN\FP\FN的數值。

# 這是一個多分類問題，y_true是target，y_pred是模型預測結果，資料格式為numpy

def cal(y_true, y_pred):

    # confusion matrix row means GT, column means predication
    name = 'save_name'
    '''畫混淆矩陣'''
    mat = confusion_matrix(y_true, y_pred)
    da = pd.DataFrame(mat, index = ['0', '1', '2'])
    sns.heatmap(da, annot =True, cbar = None, cmap = 'Blues')
    plt.title(name)
    # plt.tight_layout()yt
    plt.ylabel('True Label')
    plt.xlabel('Predict Label')
    plt.show()
    plt.savefig('{}/{}.png'.format('save_path', name)) # 將混淆矩陣圖片儲存下來
    plt.close()
    
    '''計算指標'''
    tp = np.diagonal(mat) # 每類的tp
    gt_num = np.sum(mat, axis=1) # axis = 1 指每行 ，每類的總數
    pre_num = np.sum(mat, axis=0)
    fp = pre_num - tp
    fn = gt_num - tp
    num = np.sum(gt_num)
    num = np.repeat(num, gt_num.shape[0])
    gt_num0 = num - gt_num
    tn = gt_num0 -fp
	
    recall = tp.astype(np.float32) / gt_num
    specificity = tn.astype(np.float32) / gt_num0
    precision = tp.astype(np.float32) / pre_num
    F1 = 2 * (precision * recall) / (precision + recall)
    acc = (tp + tn).astype(np.float32) / num

    print('recall:', recall, '\nmean recall:{:.4f}'.format(np.mean(recall)) )
    print('specificity:', specificity, '\nmean specificity:{:.4f}'.format(np.mean(specificity)))
    print('precision:', precision, '\nmean precision:{:.4f}'.format(np.mean(precision)))
    print('F1:', F1 , '\nmean F1:{:.4f}'.format(np.mean(F1)))
    print('acc:', acc , '\nmean acc:{:.4f}'.format(np.mean(acc)))

混淆矩陣如圖所示：

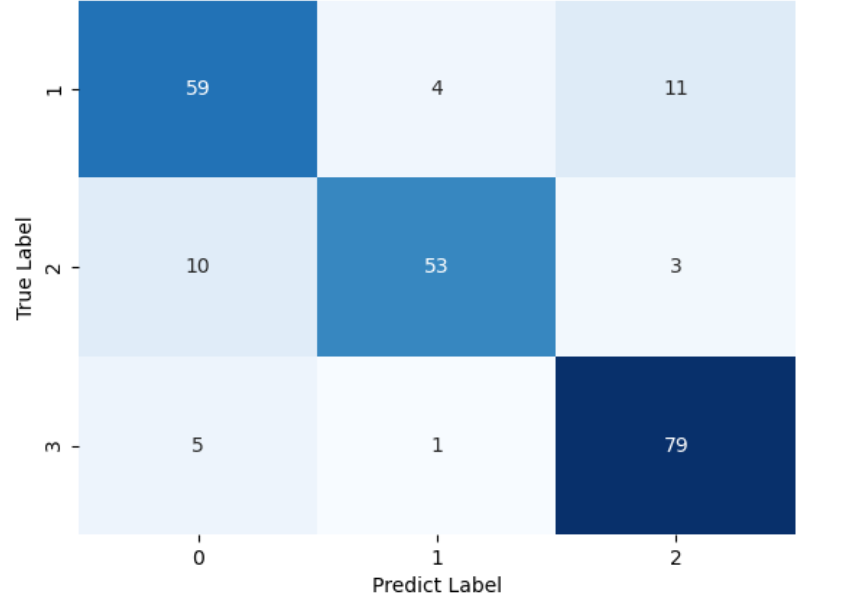
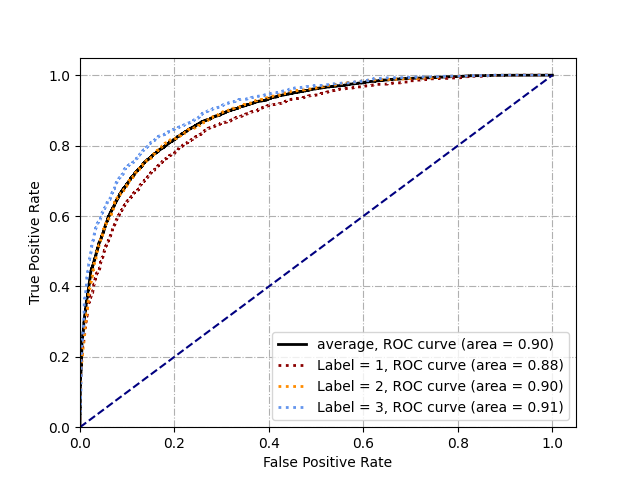
3. ROC曲線繪製及AUC計算

# 這是一個多分類問題（三分類），可以在一張圖上繪製多條ROC曲線

def paint_ROC(y_test, y_score):

    '''畫ROC曲線'''
    plt.figure()
    # 修改顏色
    colors = ['','darkred', 'darkorange', 'cornflowerblue']

    fpr = dict()
    tpr = dict()
    roc_auc = dict()
    # print('label',y_test)
    # print('score', y_score)

    label = np.zeros((len(y_test), 3),  dtype="uint8")
    for i in range(len(y_test)):
        label[i][int(y_test[i])-1] = 1
    # print('label',label)

    for i in range(1,4):
        fpr[i], tpr[i], _ = metrics.roc_curve(label[:,i-1], y_score[:, i-1])
        roc_auc[i] = metrics.auc(fpr[i], tpr[i])

    fpr["mean"], tpr["mean"], _ = metrics.roc_curve(label.ravel(), y_score.ravel())
    roc_auc["mean"] = metrics.auc(fpr["mean"], tpr["mean"])

    lw = 2
    plt.plot(fpr["mean"], tpr["mean"],
         label='average, ROC curve (area = {0:0.2f})'
               ''.format(roc_auc["mean"]),
         color='k', linewidth=lw)

    for i in range(1,4):
        auc = roc_auc[i]
        # 輸出不同類別的FPR\TPR\AUC
        print('label: {}, fpr: {}, tpr: {}, auc: {}'.format(i, np.mean(fpr[i]), np.mean(tpr[i]), auc))
        plt.plot(fpr[i], tpr[i], color=colors[i],linestyle=':',lw = lw, label='Label = {0}, ROC curve (area = {1:0.2f})'.format(i, auc))

    plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
    plt.xlim([0.0, 1.05])
    plt.ylim([0.0, 1.05])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    # plt.title('Receiver operating characteristic example')
    plt.grid(linestyle='-.')  
    plt.grid(True)
    plt.legend(loc="lower right")
    plt.show()
    # 儲存繪製好的ROC曲線
    plt.savefig('{}/{}.png'.format('save_path', 'save_name'))
    plt.close()

ROC曲線如圖所示：

[機器學習]-分類問題常用評價指標、混淆矩陣及ROC曲線繪製方法-python實現