支援向量機分類演演算法

支援向量機SVM

支援向量機原理

　　1.尋求最有分類邊界

　　　　正確：對大部分樣本可以正確的劃分類別

　　　　泛化：最大化支援向量間距

　　　　公平：與支援向量等距

　　　　簡單：線性、直線或平面，分割超平面

　　2.基於核函數的生維變換

　　　　通過名為核函數的特徵變換，增加新的特徵，使得低維度的線性不可分問題變為高維度空間中線性可分問題。

一、引論

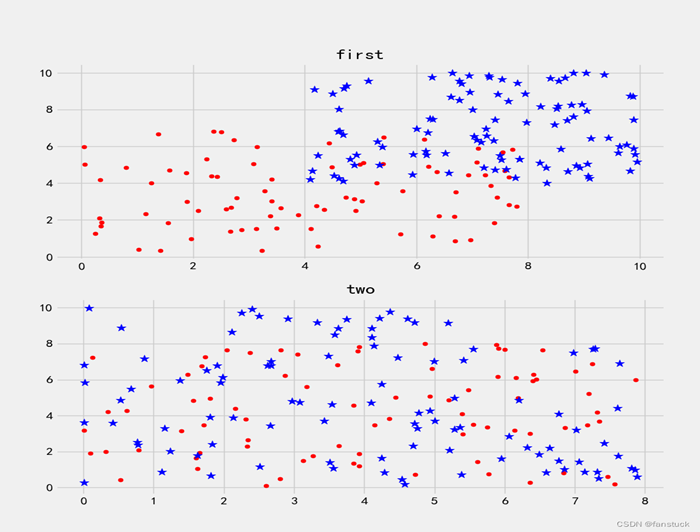
　　使用SVM支援向量機一般用於分類，得到低錯誤率的結果。SVM能夠對訓練集意外的資料點做出很好的分類決策。那麼首先我們應該從資料層面上去看SVM到底是如何做決策的，這裡來看這樣一串資料集集合在二維平面座標系上描繪的圖：

　　以迴避內積的顯式計算。

常見的核函數：

三、Python sklearn程式碼實現：

sklearn.svm.SVC語法格式為：

class sklearn.svm.SVC(  *, 
                        C=1.0, 
                        kernel='rbf',
                        degree=3, 
                        gamma='scale', 
                        coef0=0.0, 
                        shrinking=True, 
                        probability=False, 
                        tol=0.001, 
                        cache_size=200, 
                        class_weight=None, 
                        verbose=False, 
                        max_iter=- 1, 
                        decision_function_shape='ovr', 
                        break_ties=False, 
                        random_state=None)

基於鳶尾花資料的實現及解釋

程式碼如下：

 1 # 匯入模組
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 from sklearn import svm, datasets
 5 from sklearn.model_selection import train_test_split
 6 
 7 # 鳶尾花資料
 8 iris = datasets.load_iris()         #原始資料
 9 feature = iris.data[:, :2] # 為便於繪圖僅選擇2個特徵（根據前兩列資料和結果進行分類）
10 target = iris.target
11 
12 #陣列分組訓練資料和測試資料
13 x_train,x_test,y_train,y_test=train_test_split(feature,target,test_size=0.2,random_state=2020)
14 
15 # 測試樣本（繪製分類區域）,我們資料選了兩列即就是兩個特徵，所以這裡有xlist1，xlist2
16 xlist1 = np.linspace(x_train[:, 0].min(), x_train[:, 0].max(), 200)
17 xlist2 = np.linspace(x_train[:, 1].min(), x_train[:, 1].max(), 200)
18 XGrid1, XGrid2 = np.meshgrid(xlist1, xlist2)
19 # 範例化一個svm模型，非線性SVM：RBF核，超引數為0.5，正則化係數為1，SMO迭代精度1e-5, 記憶體佔用1000MB
20 svc = svm.SVC(kernel='rbf', C=1, gamma=0.5, tol=1e-5, cache_size=1000)
21 drill=svc.fit(x_train,y_train)
22 
23 #得到測試分數和測試分類
24 print(drill.score(x_test,y_test))      #測試分數
25 print(drill.predict(x_test[3].reshape(1,-1)))   #預測測試資料第三組樣本的分類或預測結果
26 
27 # 預測並繪製結果(以下都為繪圖)
28 Z = drill.predict(np.vstack([XGrid1.ravel(), XGrid2.ravel()]).T)
29 Z = Z.reshape(XGrid1.shape)
30 plt.contourf(XGrid1, XGrid2, Z, cmap=plt.cm.hsv)
31 plt.contour(XGrid1, XGrid2, Z, colors=('k',))
32 plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train, edgecolors='k', linewidth=1.5, cmap=plt.cm.hsv)
33 plt.show()