0. 寫在前面

本文將使用基於LibTorch（PyTorch C++介面）的神經網路求解器，對一維穩態對流擴散方程進行求解。研究問題參考自教科書\(^{[1]}\)範例 8.3。

1. 問題描述

一維穩態對流擴散方程為

其中，均勻恆定速度 \(u=2.0 \mathrm{m/s}\) ，運動粘性係數 \(\Gamma = 0.03 \mathrm{m^2/s}\) ，源項 \(S\) 的形式後文將敘述。

假設一維計算域長度為 \(L=1.5 \mathrm{m}\)，其上分佈有均勻恆定速度場；待求物理量為 \(\phi\)，邊界條件為左側（\(x=0\)）處給定一類邊界條件（\(\phi=0\)），右側（\(x=L\)）處給定二類邊界條件（\(\phi_{,x}=0\)）。如下圖（圖片來自教科書\(^{[1]}\)，圖8.7）所示。

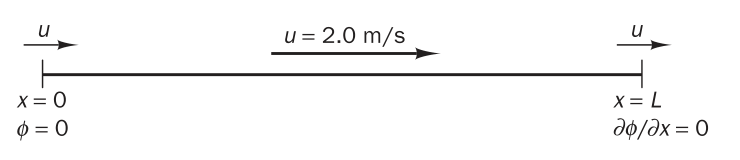
在計算域上源項分佈如下圖（圖片來自教科書\(^{[1]}\)，圖8.8）所示：

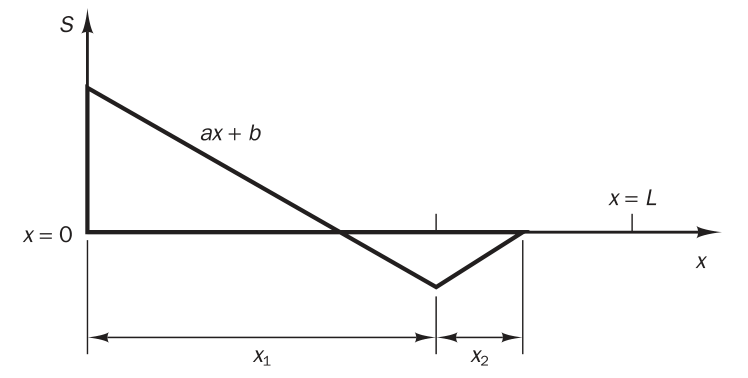
其中，\(a=-200\)，\(b=100\)，\(x_1=0.6\)，\(x_2=0.2\)。

源項數學表示式如式（1）所示。

3. 解析解

上述一維穩態對流擴散方程存在解析解（參考文獻中公式直接計算數值不對，這裡做了一些修改，如果錯了還請讀者斧正）：

其中，

使用下面程式碼繪製解析解曲線。

import math
import matplotlib.pyplot as plt

a = -200.0 # [1/m]
b =  100.0 # [1]

L = 1.5    # [m]

x_1 = 0.6  # [m]
x_2 = 0.2  # [m]

u     = 2.0  # [m/s]
Gamma = 0.03 # [m^2/s]

P     = u / Gamma # [1/m]
P2    = P * P     # [1/m^2]
expPL = math.exp( P * L )

num_terms = 20000

def a_n(n):
    if n == 0 :
        return ( ( x_1 + x_2 ) * ( a * x_1 + b ) + b * x_1 ) / ( 2.0 * L )
    else:
        alpha = n * math.pi / L
        term0 = 2.0 * L / n / n / math.pi / math.pi
        term1 = ( a * ( x_1 + x_2 ) + b ) / x_2 * math.cos( alpha * x_1  )
        term2 = a + ( a * x_1 + b ) / x_2 * math.cos( alpha * ( x_1 + x_2 ) )
        return term0 * ( term1 - term2 )

def C2():
    term0 = a_n(0) / P2 / expPL
    term1 = 0.0
    for i in range(1,num_terms + 1):
        alpha = i * math.pi / L
        coeff = ( P2 + alpha * alpha )
        term1 += a_n(i) / expPL * math.cos( i * math.pi ) / coeff

    return term0 + term1

def C1():
    term0 = C2()
    term1 = a_n(0) / P2
    term2 = 0.0
    for i in range(1,num_terms + 1):
        alpha = i * math.pi / L
        coeff = ( P2 + alpha * alpha )
        term2 += a_n(i) / coeff

    return -term0 + term1 + term2

def phi(x):
    term0 = C1()
    term1 = C2() * math.exp( P * x )
    term2 = a_n(0) / P2 * ( P * x + 1.0 )
    term3 = 0.0
    for i in range(1,num_terms + 1):
        alpha = i * math.pi / L
        coeff = ( P2 + alpha * alpha )
        term3 += a_n(i) / alpha * ( P * math.sin( alpha * x ) + alpha * math.cos( alpha * x ) ) / coeff

    return term0 + term1 - term2 - term3

x = []
y = []
num_points = 50
for i in range(num_points):
    x_ = L / ( num_points - 1 ) * i
    x.append( x_ )
    y.append( -phi(x_) * 0.75 * b / L / L ) # 這裡對參考文獻中的公式做了修改

plt.grid()
plt.xlim( 0, 1.5 )
plt.ylim( 0, 12  )
plt.plot( x, y )
plt.show()

影象如下所示：

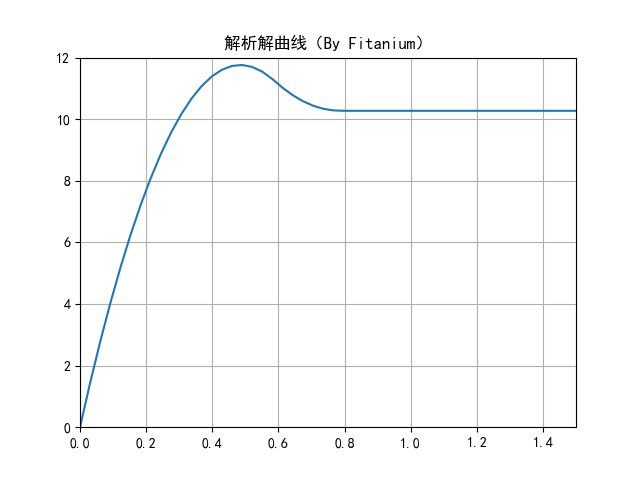
4. 神經網路

上述流暢處於穩態時，物理量 \(\phi\) 是位置 \(x\) 的函數，即 \(\phi=f(x)\)。那麼我們這裡的想法就是利用神經網路來表示這個函數，並通過利用機器學習方法（監督學習、自動微分）使該函數滿足控制方程和邊界條件。

對於上述關係，我們可以涉及類似下圖中這種全連線神經網路（使用NN-SVG繪製）。

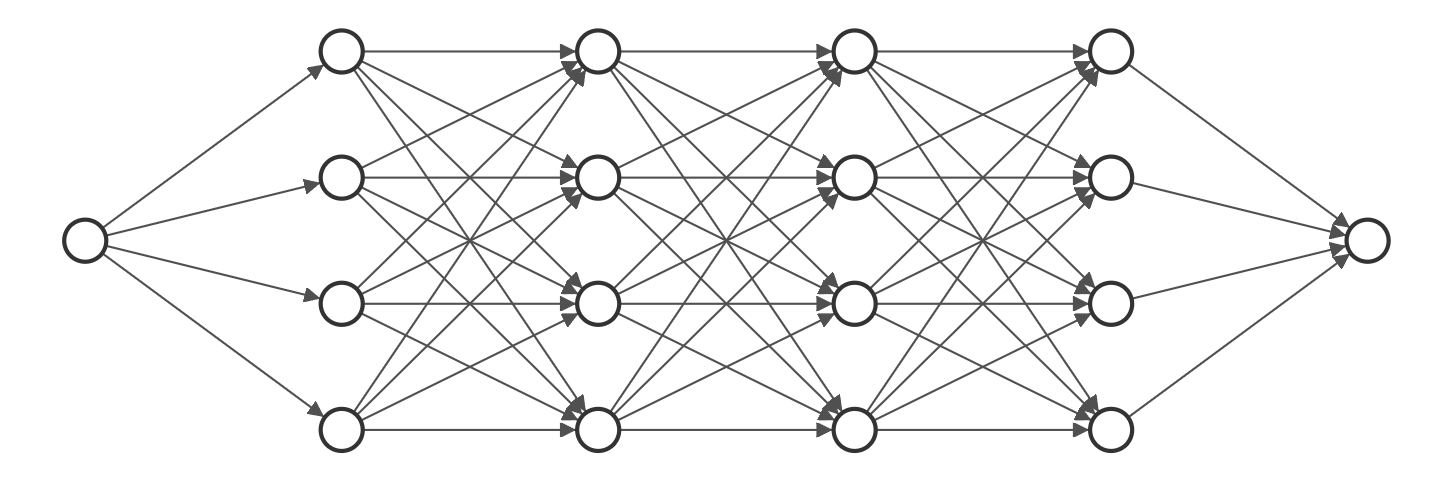
4.1 網路結構

這裡我們設定了一個含有6層神經元的全連線神經網路，形式如上圖所示，輸入層和輸出層均只有一個神經元，剩餘4個隱藏層每層含有256個神經元。

神經網路類的宣告如下，儲存在檔案 nets.hpp 檔案中，其中需要宣告向前傳播演演算法方法以及相關模組變數。

#ifndef NETS_HPP
#define NETS_HPP

#include <torch\torch.h>
// 神經網路類
class Net : public torch::nn::Module {
public:
  Net(const int inDim, const int outDim);

  torch::Tensor forward(at::Tensor x);

private:
  torch::nn::Linear input{nullptr};
  torch::nn::Linear hidden0{nullptr};
  torch::nn::Linear hidden1{nullptr};
  torch::nn::Linear hidden2{nullptr};
  torch::nn::Linear output{nullptr};
};

#endif // NETS_HPP

接下來看一下神經網路的實現，我們將其實現儲存在 nets.cpp 檔案中，其中建構函式中將初始化這些模組變數；forward 方法為向前傳播的實現，資料傳播過程為 \(1\to 256\to 256\to 256\to 256\to 1\)，網路接受一個標量輸入並最終返回一個標量輸出；另外隱藏層全部採用 tanh 函數作為啟用函數。

#include "nets.hpp"

Net::Net(const int inDim, const int outDim) {
  input = register_module("input", torch::nn::Linear(inDim, 256));
  hidden0 = register_module("hidden0", torch::nn::Linear(256, 256));
  hidden1 = register_module("hidden1", torch::nn::Linear(256, 256));
  hidden2 = register_module("hidden2", torch::nn::Linear(256, 256));
  output = register_module("output", torch::nn::Linear(256, outDim));
}

torch::Tensor Net::forward(at::Tensor x) {
  // 輸入層   : 1   --> 隱藏層 0 : 256
  torch::Tensor phi = input->forward(x);
  phi = torch::tanh(phi); // 啟用函數
  // 隱藏層 0 : 256 --> 隱藏層 1 : 256
  phi = hidden0->forward(phi);
  phi = torch::tanh(phi); // 啟用函數
  // 隱藏層 1 : 256 --> 隱藏層 2 : 256
  phi = hidden1->forward(phi);
  phi = torch::tanh(phi); // 啟用函數
  // 隱藏層 2 : 256 --> 隱藏層 3 : 256
  phi = hidden2->forward(phi);
  phi = torch::tanh(phi); // 啟用函數
  // 隱藏層 3 : 256 --> 輸出層   : 1
  phi = output->forward(phi);
  //
  return phi;
}

4.2 源項程式碼

分佈源項為分段函數，這塊比較簡單，直接給出標頭檔案和實現。

函數宣告儲存在 utils.hpp 檔案中。

#ifndef UTILS_HPP
#define UTILS_HPP

float Source(const float x);

#endif // UTILS_HPP

函數實現儲存在 utils.cpp 檔案中。

#include "utils.hpp"

float Source(const float x) {
  if (x < 0.6) {
    return -200.0 * x + 100.0;
  } else if (x > 0.8) {
    return 0.0;
  } else {
    return 100.0 * x - 80.0;
  }
}

4.3 訓練程式碼

這裡，我們將訓練程式碼儲存在 main.cpp 檔案中。由於空間位置不變，我們在迭代訓練外構造輸入引數。

程式碼實現如下所示，其中計算PDE的損失時用到了自動微分，可參考筆者之前的隨筆LibTorch 自動微分。

#include <fstream>
#include <iomanip>
#include <iostream>
#include <string>

#include "nets.hpp"
#include "utils.hpp"

int main(int argc, char *atgv[]) {
  std::cout << std::scientific << std::setprecision(7);

  const double L = 1.5;      // 計算域長度
  const int numElement = 20; // 輸入點個數

  // 構造輸入，維度為[N,1]，N行，每行為一個輸入，維度為1
  std::vector<float> x;
  for (int i = 0; i < numElement; ++i) {
    x.push_back(L / double(numElement - 1) * double(i));
  }
  torch::Tensor xT = torch::from_blob(x.data(), {numElement, 1}, torch::kFloat)
                         .requires_grad_(true);

  // 初始化神經網路和隨機梯度下降優化器
  std::shared_ptr<Net> net = std::make_shared<Net>(1, 1);
  std::shared_ptr<torch::optim::SGD> optimizer =
      std::make_shared<torch::optim::SGD>(net->parameters(), 1.e-4);

  // 開始迭代訓練
  double lossVal = 10;
  int epochIdx = 0;
  std::vector<float> sol(numElement);
  while (lossVal > 1.e-3) {
    // 向前傳播，最終輸出是一個[N,1]的輸出
    torch::Tensor out = net->forward(xT);

    // 構造損失函數（由3部分組成，PDE和兩側邊界條件）
    auto ones = torch::ones_like(out);
    torch::Tensor ddx =
        torch::autograd::grad({out}, {xT}, {ones}, true, true, false)[0];
    torch::Tensor d2dx2 =
        torch::autograd::grad({ddx}, {xT}, {ones}, true, true, false)[0];
    auto sourceTerm = torch::zeros_like(out);
    for (int i = 0; i < numElement; ++i) {
      sourceTerm[i][0] = Source(xT[i][0].item<float>());
    }
    auto pde = 2.0 * ddx - 0.03 * d2dx2;
    auto pdeLoss = torch::mse_loss(pde, sourceTerm); // 偏微分方程

    auto tag1 = torch::zeros_like(out);
    for (int i = 0; i < numElement; ++i) {
      if (i == 0) {
        tag1[i][0] = 0.0;
      } else {
        tag1[i][0] = out[i][0].item<float>();
      }
    }
    auto bndLoss1 = torch::mse_loss(out, tag1); // 左側邊界條件

    auto tag2 = torch::zeros_like(ddx);
    for (int i = 0; i < numElement; ++i) {
      if (i == numElement - 1) {
        tag2[i][0] = 0.0;
      } else {
        tag2[i][0] = ddx[i][0].item<float>();
      }
    }
    auto bndLoss2 = torch::mse_loss(ddx, tag2); // 右側邊界條件

    auto totalLoss = pdeLoss + bndLoss1 + bndLoss2;

    // 反向傳播
    optimizer->zero_grad();
    totalLoss.backward();
    optimizer->step();

    // 列印紀錄檔
    lossVal = totalLoss.item<float>();
    std::cout << "PDE_LOSS: " << pdeLoss.item<float>()
              << ", BND_LOSS1: " << bndLoss1.item<float>()
              << ", BND_LOSS2: " << bndLoss2.item<float>()
              << ", TOTAL_LOSS: " << lossVal << ", EPOCH.IDX: " << epochIdx
              << std::endl;

    epochIdx += 1;

    for (int i = 0; i < numElement; ++i) {
      sol[i] = out[i][0].item<float>();
    }
  }

  // 儲存結果
  std::ofstream os;
  os.open("solution.txt", std::ios::out);
  for (int i = 0; i < numElement; ++i) {
    os << x[i] << " " << sol[i] << std::endl;
  }
  os.close();

  return 0;
}

4.4 CMakeLists.txt

這裡使用 CMake 管理程式程式碼，內容如下所示。

cmake_minimum_required( VERSION 3.8 )

project( LibTorch)

set( CMAKE_CXX_STANDARD 14 )

set( INSTALL_PREFIX "D:/SoftwarePackage" )

## LibTorch
find_package(Torch REQUIRED PATHS "${INSTALL_PREFIX}/libtorch/share/cmake/Torch")
link_directories( "${INSTALL_PREFIX}/libtorch/lib" )

# My own code 
include_directories( . )
set(SRCS
    nets.cpp
    utils.cpp
)

set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} ${TORCH_CXX_FLAGS}" )
add_executable ( ${PROJECT_NAME} main.cpp ${SRCS} )
target_link_libraries(${PROJECT_NAME} ${TORCH_LIBRARIES} )

5. 結果處理

神經網路訓練了近4萬6千多次才滿足收斂標準，其實還是挺慢的。其中誤差最主要來自於神經網路無法滿足偏微分方程（PDE），這和很多因素有關，比如網路結構，收斂判據等。

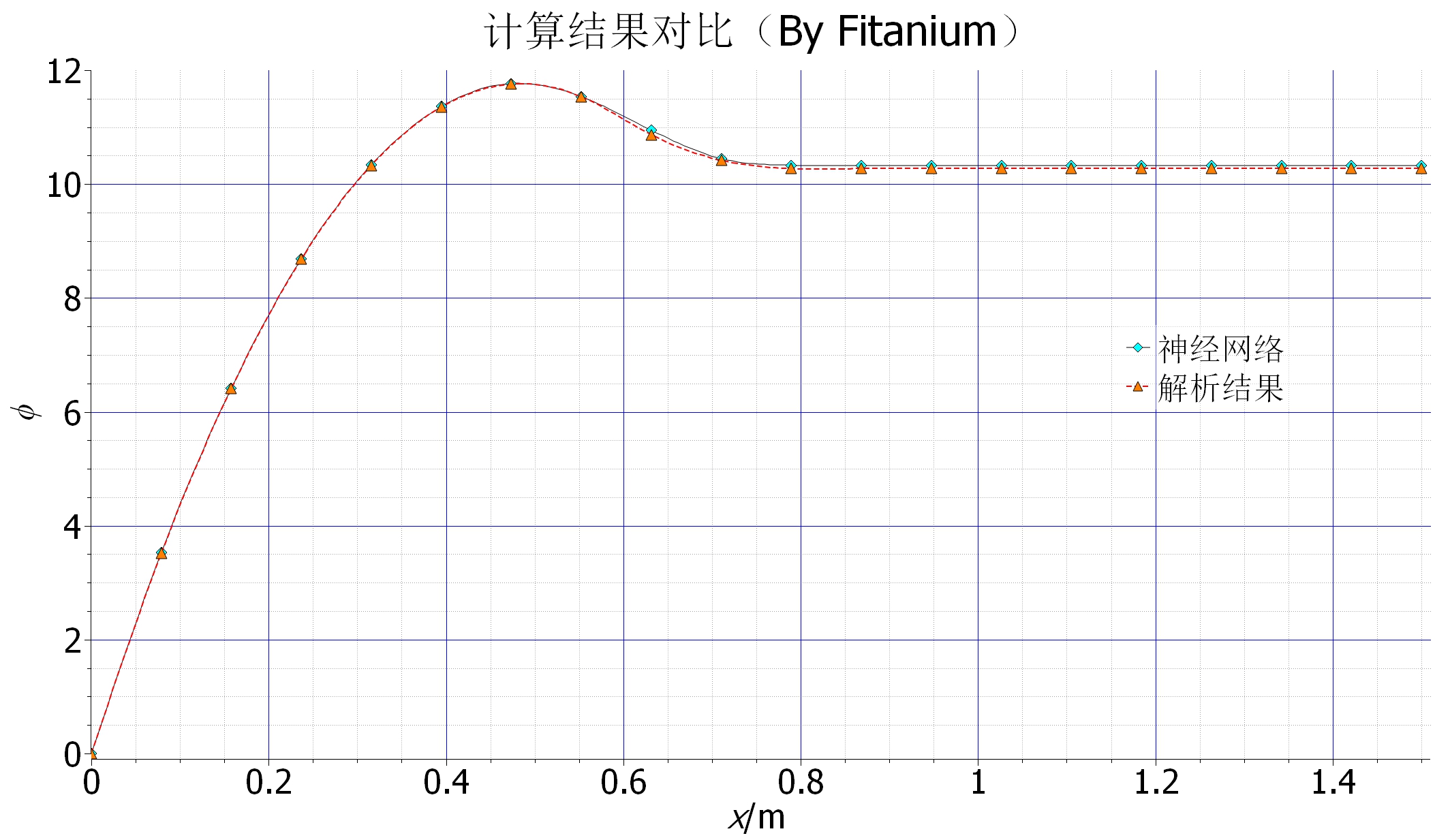
從下圖數值結果來看，訓練的神經網路給出的結果與解析解能夠較好吻合，後段有一個明顯的誤差，但是相對較小，這個誤差應該來自網路本身，網路結構簡單，改進空間應該還是比較大。

本文寫的比較簡單，也沒有使用批訓練。此外，感興趣的小夥伴可以嘗試使用OpenFOAM求解，可參考筆者之前的隨筆 OpenFOAM 程式設計 | One-Dimensional Transient Heat Conduction 。

參考文獻

[1] H. Versteeg , W. Malalasekera. Introduction to Computational Fluid Dynamics, An: The Finite Volume Method 2nd Edition[M]. Pearson. 2007.