淺談雙指標技巧（二）---通過雙指標判斷連結串列成環問題

在上一篇文章（https://www.cnblogs.com/jilodream/p/16666435.html）中，我們已經知道可以通過快慢指標，最終判斷一個單向連結串列是否成環。
一般在判斷存在環之後，還有一個經典的問題：
查詢環的起點節點是哪裡呢
力扣 142. 環形連結串列 II （https://leetcode.cn/problems/linked-list-cycle-ii/）
也就是查詢到下圖中的這個位置

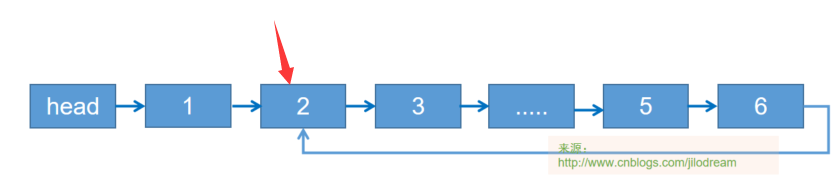
乍一看這個問題很難處理，除非像前文說的通過快取來判斷首次加入到快取中的節點外，並沒有什麼其他好的辦法。

如果直覺不能給我答案，我們往往採用數學的辦法：

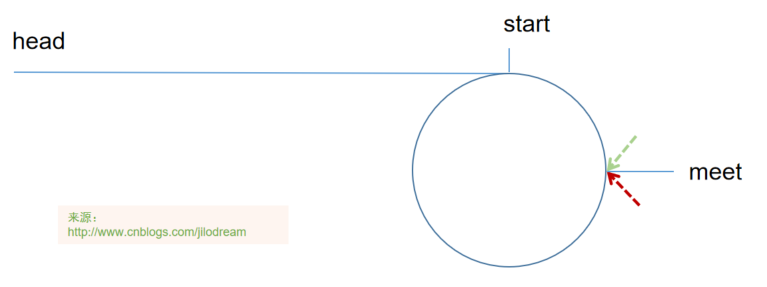
如上圖，假設判斷有環後，慢指標執行的距離是N，則快指標的執行的距離是2N。他們相遇的點是meet點。我們可以理解2N-N，也就是快指標超過慢指標的距離，其實就是圍繞meet節點繞了x圈（x>=0）。
所以最終的結論就是：

N=慢指標走的距離=快指標超過慢指標的距離=圍繞meet節點走x圈

此時我們讓兩個指標（a、b）同時走上述的兩個N，也就是一個從head節點，一個從meet節點開始，同速，一直走N步，最終會同時到達meet節點。
而這個過程的最後一部分，也就是start節點到meet節點，兩者的路徑其實是重合的。因此這兩個指標（a、b）會首先在start節點相遇，然後同時走相同的一段路徑，並最終一同走到meet節點。
如下圖：

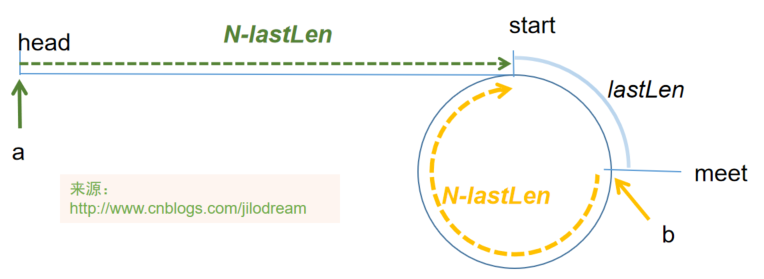
a指標移動距離=b指標移動距離=N-lastLen（lastLen表示從start節點到meet節點之間的最短距離+x*環的周長）

也就是：
a指標移動距離=b指標移動距離
所以我們在尋找環的起點start節點時，分為兩部分：
1、通過快慢指標找到二者的相遇點meet節點。
2、新定義兩個節點a、b，分別指向meet 節點和head節點。兩者按照相同的速度前進，第一次相遇的節點就是環的起始節點start

我們直接看程式碼：

 1     public ListNode detectCycle(ListNode head) {
 2         ListNode tempHead = head;
 3         if (tempHead == null) {
 4             return null;
 5         }
 6         ListNode low = tempHead;
 7         ListNode fast = tempHead;
 8         while (true) {
 9             if (fast.next == null || fast.next.next == null) {
10                 return null;
11             }
12             fast = fast.next.next;
13             low = low.next;
14             if (fast == low) {
15                 break;
16             }
17         }
18         ListNode a = tempHead;
19         ListNode b = fast;
20         while (true) {
21             if (a == b) {
22                 break;
23             }
24             a = a.next;
25             b = b.next;
26         }
27         return a;
28     }