莫比烏斯反演

沒想到吧，真的有莫比烏斯反演專題！我現在已經看不懂我當時在寫什麼了！

莫比烏斯函數

1. 定義

由唯一分解定理，可以將正整數$n$寫成$n= \prod_{i=1}^kp_i^{a_i} = p_1^{a_1}p_2^{a_2}..p_k^{a_k}$的形式，莫比烏斯函數$\mu(n)$的定義為

\[\mu(n)=\begin{cases} 1 & n=1 \\ 0 & \exist i, a_i\geq 2\\ (-1)^{k} & \forall i,a_i=1 \end{cases} \]

2. 性質

性質1

\[\sum\limits _{d|n}\mu(d)=\begin{cases} 1 & n=1 \\ 0 & n \neq 1 \end{cases} \]

證明：設$d$為$n$的約數，則$d=\prod_{i=1}^kp_i^{b_i}$，其中$0\leq b_i\leq a_i$。

對於$\mu(d)$，如果$\exist b_i\geq 2$，則$\mu(d)=0$。因此，有貢獻的$\mu(d)$一定為$C_k^i\times(-1)^i$，也就是每個質數最多取一次。

則$\sum\limits _{d|n}\mu(d)=\sum\limits _{i=0}^kC_k^i\times(-1)^i$，又$(a-b)^k=\sum\limits_{i=0}^k C_k^i a^kb^{k-i}$

$(1-1)^k=\sum\limits _{i=0}^kC_k^i\times (-1)^k$，故$\sum\limits _{d|n}\mu(d)=0^k=0$

3. 與其他數論函數的關係

(1) $\mu * I = e$

證明：設$n=\prod_{i=1}^kp_i^{a_i}, n'=\prod_{i=1}^kp_i$

則$(\mu*I)(n)=\sum\limits _{d|n}\mu(d)=\sum\limits _{d|n'}\mu(d)\\= \sum\limits _{i=0}^k(-1)^i$

呃，等等，好像性質一已經證明過了啊。$(\mu*I)(n)=[n=1]=e$，

因此，$\mu$是$I$的狄利克雷逆。

(2) $\mu * id = \varphi$

這個在基礎篇的性質證明過了QWQ，不寫辣

(3) $\mu * d=I$

證明：$(I*I)(n)=\sum\limits _{d|n}I(d)=\sum\limits _{d|n}1=d(n)$

$\therefore d=I*I$，又$\mu=I^{-1}$

$\therefore \mu * d=I$

4. 線性篩法求莫比烏斯函數

void Mobius(int n){
	mu[1] = 1;
	for (int i=2;i<=n;++i){
		if (!st[i]) p[++cnt] = i, mu[i] = -1;
		for (int j=1;p[j]<=n/i;++j){
			st[p[j] * i] = true;
			if (i % p[j] == 0) break;
			mu[p[j] * i] = -mu[i];
		}
	}
}
// 當i為質數時, 顯然mu[i]=-1
// 當p[j]為i的最小質數時, 就說明p[j]這個質數出現了>1次, 因此mu[i * p[j]] = 0
// 否則
// (1) mu[i]=0, mu[p[j] * i] = 0
// (2) mu[i]不為0, p[j] * i就相當於增加了一個質數, 因此mu[p[j] * i] = -mu[i]

莫比烏斯反演

莫反的函數定義和轉換過程大多依靠平時積累，見過類似套路，就會，沒見過，就寄。

1. 定義

設$f(n)$為數論函數(定義在正整數集合上的函數)

因數形式：

$F(n)=f*I=\sum\limits_{d|n}f(d) \Leftrightarrow f(n)=\sum\limits _{d|n}\mu(d)\times F(\frac n d)$，

證明（利用狄利克雷折積）：因為$F(n)=f*I$，則$f=F*I^{-1}=F*\mu$

即$f(n)=\sum\limits_{d|n}\mu(d)\times F(\frac n d)$。

證明（利用性質1+二重積分交換次序的思想）：

$\sum\limits_{d|n}\mu(d)\times F(\frac n d)=\sum\limits_{d|n}\mu(d)\times \sum\limits_{i|\frac n d}f(i)=\sum\limits_{i|n}f(i)\sum\limits_{d|\frac n i}\mu(d)$

（$i$能取到所有$d$可以取到的取值，這樣反過來看，把$i$提到前面）

又當且僅當$n=i$時，$\sum\limits_{d|\frac{n}i}\mu(d)=1$，因此$\sum\limits_{d|n}\mu(d)\times F(\frac n d)=f(n)$

倍數形式：

$F(n)=\sum\limits_ {n|N}f(N) \Leftrightarrow f(n)=\sum\limits_{n|N}F(N)\mu(\frac N n)$，（列舉$N$為$n$的所有倍數，$N\in[n,+\infin)$）

證明：$\sum\limits_{n|N}F(N)\mu(\frac N n)=\sum\limits_{n|N}\mu(\frac N n)\sum\limits _{N|i}f(i)$

設$d=\frac N n$，則$N=dn$，則$dn|i$，即$d|\frac i n$

因此$\sum\limits_{n|N}\mu(\frac N n)\sum\limits _{N|i}f(i)=\sum\limits_{d|\frac i n}\mu(d)\sum\limits _{N|i}f(i)$

又當且僅當$n=i$時，$\sum\limits_{d|\frac{n}i}\mu(d)=1$，因此$f(n)=\sum\limits_{n|N}F(N)\mu(\frac N n)$

運用莫反的時候，通常都是因為$F(n)$好求，但是$f(n)$不好求，因此將$f(n)$用$F,\mu$表示出來。

2. 應用1：莫反+整數分塊

p2522 Problem b

資料範圍：$1\leq n,k\leq 5\times 10^4;1\leq a\leq b\leq 5\times 10^4;1\leq c \leq d \leq 5\times 10^4$

思路：詳細的整理一下吧。

首先，題目要我們求的東西，可以先拆成一個二維字首和，$A[a,b][c,d]=A[1,b][1,d]-A[1,b][1,c-1]-A[1,a-1][1,d]+A[1,a-1][1,c-1]$。

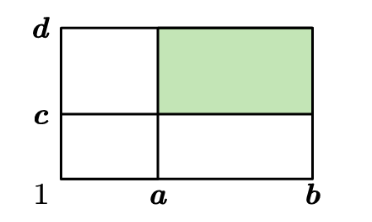
設$f(k)=\sum\limits _{x=1}^a\sum\limits _{y=1}^b[(x,y)=k]$，然後我們方便求的是這個$F(k)=\sum\limits _{x=1}^a\sum\limits _{y=1}^b[k|(x,y)]$，且$F(k)=\sum\limits _{k|N}f(N)$

則代入莫反倍數形式得$f(k)=\sum\limits _{k|N}\mu(\frac N k) F(N)$

先求$F(N)$。首先，$N|(x,y)$，也就是說，$N|x,N|y$，因此所有滿足條件的點對數量為$\lfloor \frac a N \rfloor\times \lfloor \frac b N \rfloor$

則$f(k)=\sum\limits _{k|N}\mu(\frac N k)\lfloor \frac a k \rfloor\times \lfloor \frac b k \rfloor$，設$t=\frac N k $，顯然列舉$t$的結果為$1,2,..,$這樣的整數，$N=tk$。

$f(k)=\sum\limits_{t}\mu(t)\lfloor \frac a {tk} \rfloor\times \lfloor \frac b {tk} \rfloor$，再運用整數分塊的知識進行求解即可，註釋都寫在程式碼裡吧。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> pii;
typedef pair<ll,ll> pll;
#define xx first
#define yy second
#define ls (oo << 1)
#define rs (oo << 1 | 1)
#define PI acos(-1.0)

ll read(void);

int n, cnt;
const int N = 5e4 + 5; 
int p[N], mu[N];
int pre[N];
bool st[N];

//求Mobius函數和字首和(分塊的時候用)
void Mobius(int n){
	mu[1] = 1;
	for (int i=2;i<=n;++i){
		if (!st[i]) p[++cnt] = i, mu[i] = -1;
		for (int j=1;p[j]<=n/i;++j){
			st[p[j] * i] = true;
			if (i % p[j] == 0) break;
			mu[p[j] * i] = -mu[i];
		}
	}
	for (int i=1;i<=n;++i){
		pre[i] = pre[i - 1] + mu[i];
	}
}

ll f(int a, int b, int k){
    a /= k, b /= k;
	ll res = 0, n = min(a, b), l = 1, r;
    // 在[l,r]這段,(a/l)*(b/l)為定值,那麼展開和式, 可以打包計算這一部分的和為(定值*mu的字首和)
	while (l <= n){
		r = min(n, min(a / (a / l), b / (b / l)));
		res += 1LL * (pre[r] - pre[l - 1]) * (a / l) * (b / l);
		l = r + 1;
	}
	return res;
}

void solve(){
	int a, b, c, d, k;
	a = read(), b = read(), c = read(), d = read(), k = read();
    // 二維字首和,或者說一個簡單的容斥
	ll res = f(b, d, k) - f(b, c - 1, k) - f(a - 1, d, k) + f(a - 1, c - 1, k);
	printf("%lld\n", res);
}

int main(void){
	int T;
	Mobius(N - 1);
	T = read();
	while (T--){
		solve();
	}
	
	return 0;
}

ll read(void){
    ll x = 0, f=1;char ch;
    do{ch = getchar();if (ch == '-') f=-1;}while(ch<'0' || ch>'9');
    do{x = x*10 + (ch-'0');ch = getchar();}while(ch>='0' && ch<='9');
    return x*f;
}

/*
敬告kz: 
====================================
  1. 相信自己 
  2. 看清題意, 考慮清楚再動手 
  3.   **** 今天的陣列有沒有開小呀 ？ ****  **** 今天的陣列有沒有開小呀 ？ ****
  4. 是不是想複雜了？ 
  5. 資料溢位？
  6. 陣列越界？邊界情況？ 
  6. 不要犯低階錯誤！！！ 時間複雜度？空間複雜度？精度有沒有問題？ 
====================================
* 提交的時候注意看編譯器！c++17 / c++20 / python3 
*/

3. 應用2：莫反+提取公因數

p3327約數個數和莫反+雙分塊

設$d(x)$為$x$的約數個數，給定$T$組$n,m$，求$\sum\limits _{i=1}^N \sum\limits_{j=1}^M d(i\times j)$

資料範圍：$1\leq N,M,T\leq 5\times 10^4$

$\sum\limits _{i=1}^N \sum\limits_{j=1}^M d(i\times j)=\sum\limits _{i=1}^N \sum\limits_{j=1}^M \sum\limits _{x|i} \sum\limits_{y|j} [(x,y)=1]$

證明：設$i=\prod_{i=1}^k p_i^{a_i},j=\prod_{i=1}^k p_i^{b_i}$，$0\leq a_i,b_i$

則$i\times j=\prod_{i=1}^k p_i^{a_i+b_i}$，$d(i\times j)=\prod_{i=1}^k(a_i+b_i+1)$

即從$i$中選出約數$x$，$j$中選出約數$y$，對於$p_1$而言，若要求$(x,y)=1$

則可以$x=1,y=1$，或者$x=1,y=\in[p_1,p_1^{b_1}]$，或者$x\in[p_1,p_1^{a_1}],y=1$

一共是$(a_1+b_1+1)$種取法，其他質數同理。根據乘法原理，這些取法正好就是$d(i\times j)$。

設出$f(n),F(n)$。

設$f(n)=\sum\limits _{i=1}^N \sum\limits_{j=1}^M \sum\limits _{x|i} \sum\limits_{y|j} [(x,y)=n]$，顯然$f(1)$就是答案。

設$F(n)=\sum\limits _{i=1}^N \sum\limits_{j=1}^M \sum\limits _{x|i} \sum\limits_{y|j} [n|(x,y)]$，則$F(n)=\sum\limits _{n|d}f(d)$

即$f(n)=\sum\limits _{n|d}\mu(\frac d n)F(d)$令$T=\min(N,M)$，則$f(1)=\sum\limits _{d=1}^T\mu(d)F(d)$。

再化簡$F$。

$F(n)=\sum\limits _{i=1}^N \sum\limits_{j=1}^M \sum\limits _{x|i} \sum\limits_{y|j} [n|(x,y)]=\sum\limits _{x=1}^N \sum\limits_{y=1}^M \lfloor \frac N x \rfloor \lfloor \frac M y \rfloor [n|(x,y)]$

證明：首先，$x|i,y|j$，那麼$x,y$肯定是能取到$[1,N],[1,M]$的。當$x,y$固定後，$[n|(x,y)]$和$i,j$是沒有關係的，我們可以把它提出來。那麼，裡面就變成了$\sum\limits _{i=1}^{\lfloor \frac N x \rfloor}\sum\limits _{j=1}^{\lfloor \frac M y \rfloor}1$，也就是$N,M$裡面有多少個$i,j$，它們是$x,y$的倍數，得證。

下面再消掉$[n|(x,y)]$這個條件。

設$x'=\lfloor \frac x n \rfloor,y'=\lfloor \frac y n \rfloor$

$F(n)=\sum\limits _{x=1}^N \sum\limits_{y=1}^M \lfloor \frac N x \rfloor \lfloor \frac M y \rfloor [n|(x,y)]=\sum\limits _{x'=1}^{\lfloor \frac N n \rfloor}\sum\limits _{y'=1}^{\lfloor \frac M n \rfloor}\lfloor \frac N {nx'} \rfloor\lfloor \frac M {ny'} \rfloor$

令$N'=\lfloor \frac N n \rfloor,M'=\lfloor \frac M n \rfloor$

$F(n)=\sum\limits _{x'=1}^{N'} \sum\limits_{y'=1}^{M'} \lfloor \frac {N'} {x'} \rfloor \lfloor \frac {M'} {y'} \rfloor=(\sum\limits _{x'=1}^{N'} \lfloor \frac {N'} {x'} \rfloor)\times(\sum\limits_{y'=1}^{M'} \lfloor \frac {M'} {y'} \rfloor)$

令$h(n)=\sum\limits_{i=1}^{n} \lfloor \frac {n} {i} \rfloor)$，也就是標準整數分塊，則$F(n)=h(N')\times h(M')$。

再求$f(1)$

$f(1)=\sum\limits _{d=1}^T\mu(d)h(\lfloor \frac N d \rfloor)h(\lfloor \frac M d \rfloor)$

由於$h(x)$只和$x$有關，所以可以再分一次塊，因此每次查詢複雜度$O(\sqrt N)$，總時間複雜度$O(N\sqrt N)$。

int cnt;
const int N = 5e4 + 5;
int p[N], h[N], pre[N], mu[N];
bool st[N];

void Mobius(int n){
	mu[1] = 1;
	for (int i=2;i<=n;++i){
		if (!st[i]) p[++cnt] = i, mu[i] = -1;
		for (int j=1;p[j]<=n/i;++j){
			st[p[j] * i] = true;
			if (i % p[j] == 0) break;
			mu[p[j] * i] = -mu[i];
		}
	}
	for (int i=1;i<=n;++i){
		pre[i] = pre[i - 1] + mu[i];
	}
}

void H(int n){
	for (int i=1;i<=n;++i){
		for (int l=1, r;l<=i;l=r + 1){
			r = min(i, i / (i / l));
			h[i] += (r - l + 1) * (i / l); 
		}
	}
}

void solve(){
	int n, m;
	n = read(), m = read();
	ll res = 0;
	int k = min(n, m);
	for (int l=1, r;l<=k;l=r + 1){
		r = min(k, min(n / (n / l), m / (m / l)));
		res += (ll)(pre[r] - pre[l - 1]) * h[n / l] * h[m / l];
	}
	printf("%lld\n", res);
}

int main(void){
	int T;
	Mobius(N - 1);
	H(N - 1);
	T = read();
	while (T--){
		solve();
	}
	
	return 0;
}

[數學提高] 1 莫比烏斯反演

莫比烏斯反演

莫比烏斯函數

1. 定義

2. 性質

3. 與其他數論函數的關係

4. 線性篩法求莫比烏斯函數

莫比烏斯反演

1. 定義

2. 應用1：莫反+整數分塊

3. 應用2：莫反+提取公因數