神經網路模型的引數量和計算量
其實模型的引數量好算,但浮點運算數並不好確定,我們一般也就根據引數量直接估計計算量了。但是像折積之類的運算,它的引數量比較小,但是運算量非常大,它是一種計算密集型的操作。反觀全連線結構,它的引數量非常多,但運算量並沒有顯得那麼大。
FLOPs(Floating-point Operations):浮點運算次數,理解為計算量,可以用來衡量演演算法的複雜度。一個乘法或一個加法都是一個FLOPs
FLOPS(Floating-point Operations Per Second):每秒浮點運算次數,理解為計算速度,是一個衡量硬體效能的指標。
MACCs(multiply-accumulate operations):乘-加操作次數,MACCs 大約是 FLOPs 的一半。將$w*x+b$視為一個乘法累加,也稱為1 個 MACC。
MAC(Memory Access Cost):記憶體存取成本
Params:是指模型訓練中需要訓練的引數總數
注意了:下面的闡述如果沒有特別說明,預設都是batch為1。
全連線層
全連線 權重$W$矩陣為$(C_{in}, C_{out})$,輸入$(B, F, C_{in})$,輸出$(B, F, C_{out})$。 全連線層執行的計算為:$y=matmul(x,W)+b$
$$Params=C_{in}*C_{out}+C_{out}$$
$$FLOPs=F*C_{in}*C_{out}+C_{out}$$
$$MACCs=F*C_{in}*C_{out}$$
(目前全連線層已經逐漸被 Global Average Pooling 層取代了) 注意,全連線層的權重引數量(記憶體佔用)遠遠大於折積層。
一維折積層
一維折積 kernel大小為$K$,輸入通道$C_{in}$,輸出通道$C_{out}$。輸入$(B, C_{in}, F_{in})$,輸出$(B, C_{out}, F_{out})$。
$$Params=K*C_{in}*C_{out}+C_{out}\quad(考慮bias)$$
輸出特徵圖有$(F_{out}, C_{out})$個畫素
每個畫素對應一個立體折積核$k∗C_{in}$在輸入特徵圖上做立體折積折積出來的;
$$FLOPs=C_{in}*K*F_{out}*C_{out}+C_{out}\quad(考慮bias)$$
二維折積層
折積層折積核(Kernel)的高和寬:$K[0]$和$K[1]$ 。輸入為$(N,C_{in},H_{in},W_{in})$。輸出為 $(N,C_{out},H_{out},W_{out})$,其中$H_{\text{out}}$和$W_{\text{out}}$ 分別為特徵圖的高度和寬度。
$$Params=K[0]*K[1]*C_{in}*C_{out}+C_{out}\quad(考慮bias)$$
- 輸出特徵圖中有$H_{out}*W_{out}*C_{out}$個畫素;
- 每個畫素對應一個立體折積核$k[0]*k[1]*C_{in}$在輸入特徵圖上做立體折積折積出來的;
$$MACCs=(C_{in}*K[0]*K[1])*H_{out}*W_{out}*C_{out}\quad(考慮bias)$$
其中輸出特徵圖尺寸$H_{out},W_{out}$本身又由輸入矩陣$H_{in},W_{in}$,折積尺寸K,Padding,Stride這是個引數決定:
$$H_{\text {out }}=\left\lfloor\frac{H_{in}+2 \times \text { padding }[0]-\text { dilation }[0] \times(\text { kernel_size }[0]-1)-1}{\text { stride }[0]}+1\right\rfloor$$
$$W_{\text {out }}=\left\lfloor\frac{W_{in}+2 \times \text { padding }[1]-\text { dilation }[1] \times(\text { kernel_size }[1]-1)-1}{\text { stride }[1]}+1\right\rfloor$$
那我們現在來計算一下引數量,如果瞭解折積的原理,應該也不難算出它的引數量(可能有人會說折積原理怎麼理解,這裡推薦一篇寫得通俗易懂的文章:https://zhuanlan.zhihu.com/p/77471866
分組折積
對於尺寸為$H_1×W_1×C_1$的輸入矩陣,當標準折積核的大小為$K[0], K[1], C_{in}$ ,共有$C_{out}$個折積核時,標準折積會對完整的輸入資料進行運算,最終得到的輸出矩陣尺寸為$(H_{out}, W_{out}, C_{out})$。這裡我們假設折積運算前後的特徵圖尺寸保持不變,則上述過程可以展示為下圖。
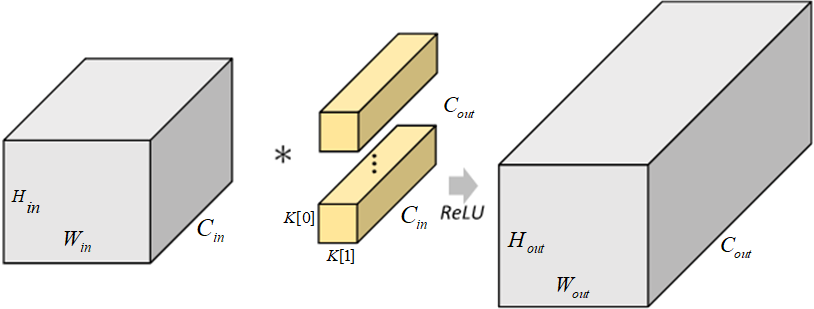
圖* 標準折積示意圖
分組折積中,通過指定組數$g$將輸入資料分成$g$組。需要注意的是,這裡的分組指的是在深度上進行分組,輸入的寬和高保持不變,即將每$C_{in}/g$個通道分為一組。因為輸入資料發生了改變,相應的折積核也需要進行對應的變化,即每個折積核的輸入通道數也就變為了$C_{in}/g$,而折積核的大小是不需要改變的。同時,每組的折積核個數也由原來的$C_{out}$變為$C_{out}/g$。對於每個組內的折積運算,同樣採用標準折積運算的計算方式,這樣就可以得到$g$組尺寸為$H_{out}, W_{out},C_{out}/g$的輸出矩陣,最終將這$g$組輸出矩陣進行拼接就可以得到最終的結果。這樣拼接完成後,最終的輸出尺寸就可以保持不變,仍然是$H_{out}, W_{out}, C_{out}$。分組折積的運算過程如下圖所示。
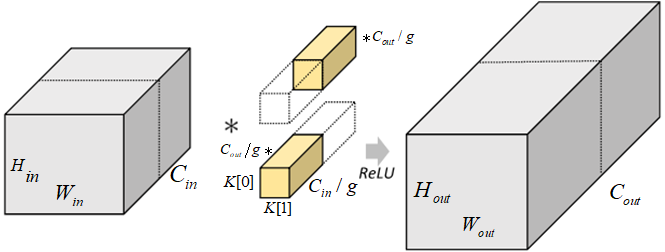
圖 分組折積示意圖
使用分組折積後,引數和計算量則變為:
$$Params=K[0]*K[1]*\frac{C_{in}}{g}*\frac{C_{out}}{g}*g=K[0]*K[1]*C_{in}*C_{out}*\frac{1}{g}$$
$$MACCs=(\frac{C_{in}}{g}*K[0]*K[1])*H_{out}·W_{out}*\frac{C_{out}}{g}*g\\
=(C_{in}*K[0]·K[1])*H_{out}·W_{out}*C_{out}*\frac{1}{g}$$
深度可分離折積層
深度可分離折積是將常規折積因式分解為兩個較小的運算,它們在一起佔用的記憶體更少(權重更少),並且速度更快。深度可分離折積中,
- 先進行 深度折積,與常規折積相似,不同之處在於將輸入通道分groups組,groups等於輸入通道數。深度折積輸入通道數和輸出通道數相等
- 在進行 逐點折積,也就是1x1折積
class DepthwiseSeparableConv(nn.Module): def __init__(self, in_channels, out_channels, kernel_size, stride, padding, dilation, bias): super(DepthwiseSeparableConv, self).__init__() # Use `groups` option to implement depthwise convolution depthwise_conv = nn.Conv1d(in_channels, in_channels, kernel_size, stride=stride, padding=padding, dilation=dilation, groups=in_channels, bias=bias) pointwise_conv = nn.Conv1d(in_channels, out_channels, 1, bias=bias) self.net = nn.Sequential(depthwise_conv, pointwise_conv) def forward(self, x): return self.net(x)
標準折積為:
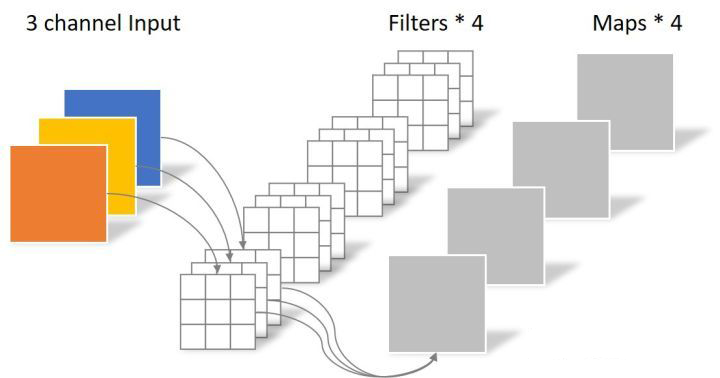
深度折積,將輸入分成$C_{in}$組,$C_{in}=C_{out}$
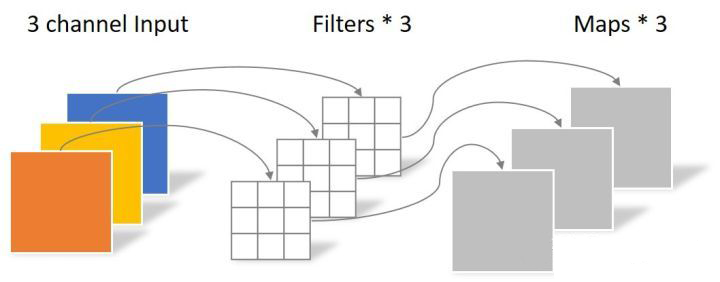
逐點折積
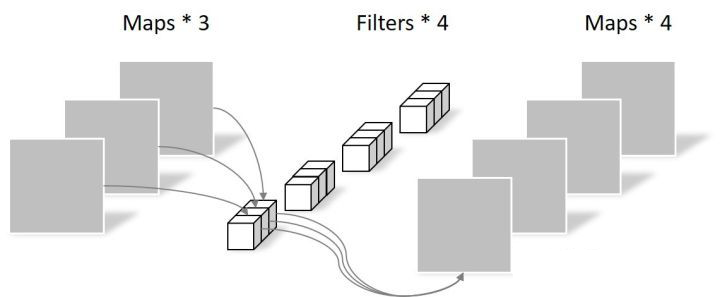
所以深度可分離折積的引數量和計算量為:
$$Params=K[0]*K[1]*C_{in}*C_{out}*\frac{1}{C_{in}}+1*1*C_{in}*C_{out}=K[0]*K[1]*C_{out}+C_{in}*C_{out}$$
$$MACC=\begin{aligned}
M A C C s &=\left(C_{\text {in }} * K[0] \cdot K[1]\right) * H_{\text {out }} * W_{\text {out }} * C_{\text {out }} * \frac{1}{C_{\text {in }}}+\left(C_{\text {in }} * 1 * 1\right) * H_{\text {out }} \cdot W_{\text {out }} * C_{\text {out }} \\
&=K[0] \cdot K[1] * H_{\text {out }} \cdot W_{\text {out }} * C_{\text {out }}+C_{\text {in }} * H_{\text {out }} * W_{\text {out }} * C_{\text {out }}
\end{aligned}$$
LSTM層
關於LSTM的原理可以參考這一篇文章:迴圈神經網路(RNN)及衍生LSTM、GRU詳解,如果想要算清楚,請務必要看,由於相似內容太多我就不搬移過來了
$$Params=C_{in}*(hidden\_size*4)+hidden\_size*hidden\_size*4$$
一個time_step的LSTM計算量為:
$$MACCs = 1*C_{in}*hidden\_size*4+hidden\_size*hidden\_size*4+hidden\_size*hidden\_size$$
第三庫計算工具
模型引數數量(params):指模型含有多少引數,直接決定模型的大小,也影響推斷時對記憶體的佔用量,單位通常為 M,GPU 端通常引數用 float32 表示,所以模型大小是引數數量的 4 倍。
以AlexNet模型為例

import torch import torch.nn as nn import torchvision class AlexNet(nn.Module): def __init__(self,num_classes=1000): super(AlexNet,self).__init__() self.feature_extraction = nn.Sequential( nn.Conv2d(in_channels=3,out_channels=96,kernel_size=11,stride=4,padding=2,bias=False), nn.ReLU(inplace=True), nn.MaxPool2d(kernel_size=3,stride=2,padding=0), nn.Conv2d(in_channels=96,out_channels=192,kernel_size=5,stride=1,padding=2,bias=False), nn.ReLU(inplace=True), nn.MaxPool2d(kernel_size=3,stride=2,padding=0), nn.Conv2d(in_channels=192,out_channels=384,kernel_size=3,stride=1,padding=1,bias=False), nn.ReLU(inplace=True), nn.Conv2d(in_channels=384,out_channels=256,kernel_size=3,stride=1,padding=1,bias=False), nn.ReLU(inplace=True), nn.Conv2d(in_channels=256,out_channels=256,kernel_size=3,stride=1,padding=1,bias=False), nn.ReLU(inplace=True), nn.MaxPool2d(kernel_size=3, stride=2, padding=0), ) self.classifier = nn.Sequential( nn.Dropout(p=0.5), nn.Linear(in_features=256*6*6,out_features=4096), nn.ReLU(inplace=True), nn.Dropout(p=0.5), nn.Linear(in_features=4096, out_features=4096), nn.ReLU(inplace=True), nn.Linear(in_features=4096, out_features=num_classes), ) def forward(self,x): x = self.feature_extraction(x) x = x.view(x.size(0),256*6*6) x = self.classifier(x) return x if __name__ =='__main__': # model = torchvision.models.AlexNet() model = AlexNet() # 列印模型引數 #for param in model.parameters(): #print(param) #列印模型名稱與shape for name,parameters in model.named_parameters(): print(name,':',parameters.size())
計算引數量與可訓練引數量
def get_parameter_number(model): total_num = sum(p.numel() for p in model.parameters()) trainable_num = sum(p.numel() for p in model.parameters() if p.requires_grad) return {'Total': total_num, 'Trainable': trainable_num} total_num, trainable_num = get_parameter_number(model) print("trainable_num/total_num: %.2fM/%.2fM" % (trainable_num / 1e6, total_num / 1e6))
torchsummary
import torchsummary as summary summary.summary(model, (3, 224, 224))
列印結果

---------------------------------------------------------------- Layer (type) Output Shape Param # ================================================================ Conv2d-1 [-1, 96, 55, 55] 34,848 ReLU-2 [-1, 96, 55, 55] 0 MaxPool2d-3 [-1, 96, 27, 27] 0 Conv2d-4 [-1, 192, 27, 27] 460,800 ReLU-5 [-1, 192, 27, 27] 0 MaxPool2d-6 [-1, 192, 13, 13] 0 Conv2d-7 [-1, 384, 13, 13] 663,552 ReLU-8 [-1, 384, 13, 13] 0 Conv2d-9 [-1, 256, 13, 13] 884,736 ReLU-10 [-1, 256, 13, 13] 0 Conv2d-11 [-1, 256, 13, 13] 589,824 ReLU-12 [-1, 256, 13, 13] 0 MaxPool2d-13 [-1, 256, 6, 6] 0 Dropout-14 [-1, 9216] 0 Linear-15 [-1, 4096] 37,752,832 ReLU-16 [-1, 4096] 0 Dropout-17 [-1, 4096] 0 Linear-18 [-1, 4096] 16,781,312 ReLU-19 [-1, 4096] 0 Linear-20 [-1, 1000] 4,097,000 ================================================================ Total params: 61,264,904 Trainable params: 61,264,904 Non-trainable params: 0 ---------------------------------------------------------------- Input size (MB): 0.57 Forward/backward pass size (MB): 9.96 Params size (MB): 233.71 Estimated Total Size (MB): 244.24 ----------------------------------------------------------------
torchstat
from torchstat import stat stat(model, (3, 224, 224)) # Total params: 61,264,904 # ------------------------------------------ # Total memory: 4.98MB # Total MAdd: 1.72GMAdd # Total Flops: 862.36MFlops # Total MemR+W: 244.14MB
thop
from thop import profile input = torch.randn(1, 3, 224, 224) flops, params = profile(model, inputs=(input, )) print(flops, params) # 861301280.0 61264904.0
ptflops
from ptflops import get_model_complexity_info flops, params = get_model_complexity_info(model, (3, 224, 224), as_strings=True, print_per_layer_stat=True) print('Flops: ' + flops) print('Params: ' + params)
複雜度對模型的影響
- 時間複雜度決定了模型的訓練/預測時間。如果複雜度過高,則會導致模型訓練和預測耗費大量時間,既無法快速的驗證想法和改善模型,也無法做到快速的預測。
- 空間複雜度決定了模型的引數數量。由於維度詛咒的限制,模型的引數越多,訓練模型所需的資料量就越大,而現實生活中的資料集通常不會太大,這會導致模型的訓練更容易過擬合。
- 當我們需要裁剪模型時,由於折積核的空間尺寸通常已經很小(3x3),而網路的深度又與模型的表徵能力緊密相關,不宜過多削減,因此模型裁剪通常最先下手的地方就是通道數。
Inception 系列模型是如何優化複雜度的
Inception V1中的 1*1 折積降維同時優化時間複雜度和空間複雜度

Inception V1中使用 GAP 代替 Flatten
Inception V2中使用 兩個3*3折積級聯代替5*5折積分支
Inception V3中使用 N*1與1*N折積級聯代替N*N折積
Xception 中使用 深度可分離折積(Depth-wise Separable Convolution)

參考文獻
【知乎】折積神經網路的複雜度分析
【知乎】神經網路模型複雜度分析
【知乎】深度可分離折積
