技術背景

在前面的幾篇文章中我們分別介紹過numpy中的愛因斯坦求和函數Einsum和MindSpore框架中的愛因斯坦求和運算元Einsum的基本用法。而我們需要知道，愛因斯坦求和其實還可以實現非常多的功能，甚至可以替代大部分的矩陣運算，比如常見的點乘、元素乘、求和等等這些都是可以的。那我們就逐一看一下可以用愛因斯坦求和來替代的那些函數和方法。

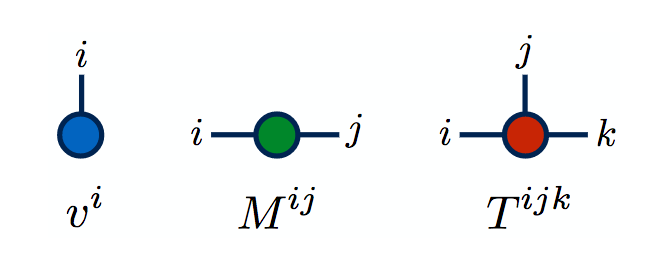
案例演示

在numpy、Jax框架和MindSpore框架中都是支援愛因斯坦求和算符的，那麼這裡為了方便演示，我們採用的是numpy來做一些參考案例:

In [1]: import numpy as np

In [2]: x = np.arange(3)

In [3]: x
Out[3]: array([0, 1, 2])

In [4]: y = np.arange(3, 6)

In [5]: y
Out[5]: array([3, 4, 5])

In [6]: P = np.arange(1, 10).reshape(3,3)

In [7]: P
Out[7]: 
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

矩陣轉置

矩陣轉置，或者是調換矩陣的某兩個維度，這個功能用愛因斯坦求和來做是非常清晰的，我們先看一下相應的公式：

\[P^T=\left[ \begin{matrix} P_{00}&P_{01}&P_{02}\\ P_{10}&P_{11}&P_{12}\\ P_{20}&P_{21}&P_{22} \end{matrix} \right]^T= \left[ \begin{matrix} P_{00}&P_{10}&P_{20}\\ P_{01}&P_{11}&P_{21}\\ P_{02}&P_{12}&P_{22} \end{matrix} \right] \]

一般矩陣轉置我們如果用numpy來操作的話，只需要使用P=P.T就可以了，而這個功能用愛因斯坦求和運算元也是可以實現的：

In [40]: np.allclose(P.T, np.einsum('kl->lk', P))
Out[40]: True

這裡有一個比較有意思的事情是，如果不指定生成的序號，但是給定的愛因斯坦算符順序如果前面的大於後面的，也可以實現矩陣轉置的功能，比如下面的一個案例：

In [41]: np.allclose(P.T, np.einsum('ji', P))
Out[41]: True

元素乘

對應於兩個矩陣（向量、張量）之間的元素乘法，普通操作我們可以直接用\(x*y\)來實現（假定維度大小為3）：

\[x*y = \left[ \begin{matrix} x_0\\x_1\\x_2 \end{matrix} \right]* \left[ \begin{matrix} y_0\\y_1\\y_2 \end{matrix} \right]=\left[ \begin{matrix} x_0y_0\\x_1y_1\\x_2y_2 \end{matrix} \right] \]

對應於程式碼實現：

In [8]: np.allclose(x*y, np.einsum('k,k->k', x, y))
Out[8]: True

矩陣內求和

把矩陣中的所有元素相加：

\[SUM(x)=SUM(\left[ \begin{matrix} x_0\\x_1\\x_2 \end{matrix} \right])=x_0+x_1+x_2 \]

對應於Python程式碼實現為：

In [9]: np.allclose(np.sum(x), np.einsum('k->', x))
Out[9]: True

In [12]: np.allclose(np.sum(P), np.einsum('kl->', P))
Out[12]: True

In [13]: np.allclose(np.sum(P, axis=-1), np.einsum('kl->k', P))
Out[13]: True

In [14]: np.allclose(np.sum(P, axis=0), np.einsum('kl->l', P))
Out[14]: True

那麼，既然求和能算，同樣的平均值也是可以計算的，這裡就不展開介紹了。

矩陣點乘

這個應用場景很多，比如當我們需要計算兩個向量之間的夾角的時候，就會用到矩陣點乘。矩陣點乘的定義如下：

\[x\cdot y = \left[ \begin{matrix} x_0\\x_1\\x_2 \end{matrix} \right]\cdot \left[ \begin{matrix} y_0\\y_1\\y_2 \end{matrix} \right]=x_0y_0+x_1y_1+x_2y_2 \]

對應的Python程式碼實現如下所示：

In [15]: np.allclose(np.dot(x, y), np.einsum('k,k->', x, y))
Out[15]: True

矩陣向量乘

這個應用場景也非常多，比如我們經常所用到的向量的伸縮、旋轉等，都可以用一系列的矩陣作用在一個向量上來表示，相關的計算公式為：

\[P\cdot x=\left[ \begin{matrix} P_{00}&P_{01}&P_{02}\\ P_{10}&P_{11}&P_{12}\\ P_{20}&P_{21}&P_{22} \end{matrix} \right]\cdot \left[ \begin{matrix} x_0\\x_1\\x_2 \end{matrix} \right]= \left[ \begin{matrix} P_{00}x_0+P_{01}x_1+P_{02}x_2\\P_{10}x_0+P_{11}x_1+P_{12}x_2\\P_{20}x_0+P_{21}x_1+P_{22}x_2 \end{matrix} \right] \]

對應的Python程式碼如下所示：

In [16]: np.allclose(np.dot(P, x), np.einsum('kl,l->k', P, x))
Out[16]: True

In [25]: np.allclose(np.dot(P, x[:, None]), np.einsum('kl,lm->km', P, x[:, None]))
Out[25]: True

In [31]: np.allclose(np.dot(P, P.T), np.einsum('kl,lm->km', P, P.T))
Out[31]: True

在上述案例中我們還包含了矩陣跟矩陣之間的乘法，這些基本運算都是可以通用的。

克羅內克積

克羅內克積，又叫張量積，比如兩個向量或者矩陣之間沒有耦合關係，那麼可以用一個克羅內克積來總體表示這兩個向量或者矩陣組成的向量或者矩陣，該運算被定義為：

\[x\otimes y^{T}=\left[ \begin{matrix} x_0\\x_1\\x_2 \end{matrix} \right]\otimes \left[y_0, y_1, y_2\right]=\left[ \begin{matrix} x_0y_0&x_0y_1&x_0y_2\\ x_1y_0&x_1y_1&x_1y_2\\ x_2y_0&x_2y_1&x_2y_2 \end{matrix} \right] \]

對應Python程式碼實現如下所示：

In [36]: np.allclose(np.kron(x[:, None], y), np.einsum('kl,l->kl', x[:, None], y))
Out[36]: True

In [37]: np.allclose(np.kron(x, y), np.einsum('kl,l->kl', x[:, None], y).reshape(9))
Out[37]: True

需要注意的是，愛因斯坦求和運算只能減少總的維度數量，但是不可改變維度大小，因此有時候會需要用到reshape的功能配合使用。

取對角元

這個應用也好理解，就是把矩陣的每一個對角元素取出來，用公式描述就是：

\[diag(P)=diag(\left[ \begin{matrix} P_{00}&P_{01}&P_{02}\\ P_{10}&P_{11}&P_{12}\\ P_{20}&P_{21}&P_{22} \end{matrix} \right])=\left[P_{00}, P_{11}, P_{22}\right] \]

相關的Python程式碼實現如下所示：

In [46]: np.allclose(np.diag(P), np.einsum('ii->i', P))
Out[46]: True

求矩陣跡

矩陣的跡（Trace），就是對所有的對角元進行求和，那麼有了上一步使用愛因斯坦求和函數提取所有的對角元之後，其實我們可以稍微調整一下，就能得到求矩陣跡的方法。首先看下矩陣跡的公式定義：

\[Tr(P) = Tr(\left[ \begin{matrix} P_{00}&P_{01}&P_{02}\\ P_{10}&P_{11}&P_{12}\\ P_{20}&P_{21}&P_{22} \end{matrix} \right])=P_{00}+P_{11}+P_{22} \]

相關的Python程式碼實現如下所示：

In [47]: np.allclose(np.trace(P), np.einsum('ii->', P))
Out[47]: True

多重運算

有時候會涉及到一系列的矩陣按照順序作用在一個向量上，如果從張量的角度來考慮的話，其中的維度還可以非常靈活的變化，不一定全都是方陣。應該說，這也是愛因斯坦求和運算元的重大意義所在。如果不使用愛因斯坦求和運算元，那麼要計算\(A\cdot B\cdot C\cdot x\)這樣的一個過程，可以多次巢狀使用numpy的dot點乘函數。但是這樣比較麻煩，一般推薦可以使用numpy中的另外一個函數：multi_dot，相關的Python程式碼實現如下所示：

In [39]: np.allclose(np.linalg.multi_dot((P, P, P, x)), np.einsum('ij,jk,kl,l->i', P, P, P, x))
Out[39]: True

在這種多重運算的過程中，可以使用einsum_path去找到一條更好的歸併路徑，以達到提升演演算法效能的效果。

總結概要

本文主要基於Python的Numpy庫，介紹一些愛因斯坦求和運算元Einsum的應用場景，包括求和、求內外積、求轉置等等。我們需要明確的是，愛因斯坦求和運算元的意義主要在於矩陣的多重運算時，可以通過愛因斯坦求和約定將這種複雜問題定義成一個張量網路，通過圖模型去找到一個更好的縮並路徑，以得到更好的演演算法複雜度。而如果只是普通的點乘求和之類的運算，其實並不是Einsum的主要功能。但是這些功能也可以用愛因斯坦求和的形式來實現，也說明了這個約定的先進性。當然，也有眾多的矩陣運算功能是無法直接通過愛因斯坦求和運算元來實現的，比如矩陣求逆、求本徵值、矩陣擴維、矩陣重構還有向量叉乘等等。只有在合適的地方使用Einsum，才能體現它的真正價值。