【短道速滑九】仿halcon中gauss_filter小半徑高斯模糊優化的實現

通常，我們談的高斯模糊，都知道其是可以行列分離的演演算法，現在也有著各種優化演演算法實現，而且其速度基本是和引數大小無關的。但是，在我們實際的應用中，我們可能會發現，有至少50%以上的場景中，我們並不需要大半徑的高斯，反而是微小半徑的模糊更有用武之地（比如Canny的預處理、簡單去噪等），因此，小半徑的高斯是否能進一步加速就值的研究，正因為如此，一些商業軟體都提供了類似的功能，比如在halon中，直接的高斯模糊可以用smooth_image實現，但是你在其幫助檔案中搜尋gauss關鍵字後，你會發現有以下兩個函數：

　　　　gauss_filter — Smooth using discrete gauss functions.

　　　　gauss_image — Smooth an image using discrete Gaussian functions.

兩個函數的功能描述基本是一個意思，但是在gauss_image函數的註釋下有這麼一條：

　　　　gauss_image is obsolete and is only provided for reasons of backward compatibility. New applications should use the operator gauss_filter instead.

即這個函數已經過時，提供他只是為了向前相容，新的應用建議使用gauss_filter 函數，那我們再來看下halcon中其具體的描述：

　　Signature

　　　　gauss_filter(Image : ImageGauss : Size : )

　　Description

　　　　The operator gauss_filter smoothes images using the discrete Gaussian, a discrete approximation of the Gaussian function,

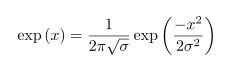
　　The smoothing effect increases with increasing filter size. The following filter sizes (Size) are supported (the sigma value of the gauss function is indicated in brackets):

　　　　　　　　3 (0.600)
　　　　　　　　5 (1.075)
　　　　　　　　7 (1.550)
　　　　　　　　9 (2.025)
　　　　　　　　11 (2.550)
　　　　For border treatment the gray values of the images are reflected at the image borders. Notice that, contrary to the operator gauss_image, the relationship between the filter mask size and its respective value for the sigma parameter is linear.

　　可見gauss_filter的Size只能取3、5、7、9、11這五個值，括號裡給出了對應的sigma值。

　　這種小半徑的模糊的優化其實在我部落格里有講過好幾個這方面的。但是前面講述的基本都是直徑不超過5，半徑不大於2的，比如這裡的3和5就可以直接用那種方法處理。

　　我們先來看看這個權重怎麼計算：

　　簡單的例子，比如Size=3時，其實就是一個3*3的折積，這個3*3的折積核可以用下述方式計算出來：

    const int Diameter = 3, Radius = 1;
    float Sum = 0, Delta = 0.600, Weight[Diameter][Diameter];
    for (int Y = 0; Y < Diameter; Y++)
    {
        for (int X = 0; X < Diameter; X++)
        {
            Weight[X][Y] = exp(-((X - Radius) * (X - Radius) + (Y - Radius) * (Y - Radius)) / (2 * Delta * Delta));
            Sum += Weight[X][Y];
        }
    }
    //    0.027682    0.111015    0.027682
    //    0.111015    0.445213    0.111015
    //    0.027682    0.111015    0.027682
    for (int Y = 0; Y < Diameter; Y++)
    {
        for (int X = 0; X < Diameter; X++)
        {
            Weight[X][Y] /= Sum;
        }
    }

　　注意折積和要中心對稱。

　　要計算這個3*3的折積，可以直接用浮點資料計算，很明顯，這裡我們可以直接硬計算，而無需其他什麼優化技巧，但是為了不必要的浮點計算，我們很明顯可以把這個折積核定點話，弄成整數，比如整體乘以16384倍，得到下面的折積核：

// 　　454 1819 454
//    1819 7292 1819
//    454 1819 454

　　這樣，就可以直接藉助整數的乘法和一個移位來得到最終的結果值。

　　另外，還有一個特點，就是藉助於SIMD執行還可以是實現一次性進行4個整數的計算，如果在厲害一點，還可以使用_mm_madd_epi16這個特別的SIMD指令，一次性實現8位元整數的計算，效率大大的提高。

　　有興趣的可以找找我以前的博文。

　　當半徑大於3時，在使用直接折積就帶來了一定的效能問題，比如直徑為7時，每個點的計算量有49次了，這個時候即使藉助於SSE也會發現，其耗時和優化後的任意核的高斯相比已經不具有任何優勢了，當半徑進一步加大時，反而超過了任何核心的優化效果，這個時候我們就需要使用另外一個特性了，即高斯折積的行列分離特性。我們以9*9的高斯折積核為例：

　　使用類似上面的程式碼，可以得到這個時候的歸一化的高斯折積核如下：

    //    0.000825    0.001936    0.003562    0.005135    0.005801    0.005135    0.003562    0.001936    0.000825
    //    0.001936    0.004545    0.008363    0.012056    0.013619    0.012056    0.008363    0.004545    0.001936
    //    0.003562    0.008363    0.015386    0.022181    0.025057    0.022181    0.015386    0.008363    0.003562
    //    0.005135    0.012056    0.022181    0.031977    0.036124    0.031977    0.022181    0.012056    0.005135
    //    0.005801    0.013619    0.025057    0.036124    0.040809    0.036124    0.025057    0.013619    0.005801
    //    0.005135    0.012056    0.022181    0.031977    0.036124    0.031977    0.022181    0.012056    0.005135
    //    0.003562    0.008363    0.015386    0.022181    0.025057    0.022181    0.015386    0.008363    0.003562
    //    0.001936    0.004545    0.008363    0.012056    0.013619    0.012056    0.008363    0.004545    0.001936
    //    0.000825    0.001936    0.003562    0.005135    0.005801    0.005135    0.003562    0.001936    0.000825

　　我們看到這個折積核其轉置後的結果和原型一模一樣，這樣的折積核就具有行列可分離性，我們要得到其可分離的折積列向量或者行列量，可以通過歸一化其第一行或者第一列的得到，比如將上述核心第一行歸一化後得到：

0.028714    0.067419    0.124039    0.178822    0.202011    0.178822    0.124039      0.067419    0.028714

　　用matlab驗證下：

>> a=[0.028714    0.067419    0.124039    0.178822    0.202011    0.178822    0.124039 0.067419    0.028714]

a =

    0.0287    0.0674    0.1240    0.1788    0.2020    0.1788    0.1240    0.0674    0.0287

>> a'*a

ans =

    0.0008    0.0019    0.0036    0.0051    0.0058    0.0051    0.0036    0.0019    0.0008
    0.0019    0.0045    0.0084    0.0121    0.0136    0.0121    0.0084    0.0045    0.0019
    0.0036    0.0084    0.0154    0.0222    0.0251    0.0222    0.0154    0.0084    0.0036
    0.0051    0.0121    0.0222    0.0320    0.0361    0.0320    0.0222    0.0121    0.0051
    0.0058    0.0136    0.0251    0.0361    0.0408    0.0361    0.0251    0.0136    0.0058
    0.0051    0.0121    0.0222    0.0320    0.0361    0.0320    0.0222    0.0121    0.0051
    0.0036    0.0084    0.0154    0.0222    0.0251    0.0222    0.0154    0.0084    0.0036
    0.0019    0.0045    0.0084    0.0121    0.0136    0.0121    0.0084    0.0045    0.0019
    0.0008    0.0019    0.0036    0.0051    0.0058    0.0051    0.0036    0.0019    0.0008

　　和前面計算的核是一致的。

　　這個時候的策略就需要改變了，不能直接計算，我們分配一個臨時的中國記憶體，考慮到精度問題，建議中間記憶體至少使用short型別。我們對原始資料先進行行方向的一維折積，並取適當的移位資料，將這個中間結果保留在臨時的記憶體中，然後在對臨時記憶體記性列方向的折積，儲存到目標中，考慮到折積時邊緣部分會超出邊界，所以還可以使用一個臨時擴充套件的記憶體，提前把邊界位置的內容設計好並填充進去，計算時，就可以連續存取了。

　　其實這裡也有兩種選擇，即先只計算那些領域不會超出邊界的中心畫素（使用SIMD優化），然後再用普通的C程式碼組防邊界溢位的普通演演算法，但是測試發現，這些普通的C程式碼的耗時佔整體的比例有點誇張了，還不如前面的做個臨時擴充套件記憶體來的快速和方便。

　　同樣的道理，水平和垂直方向的一維折積也應該用定點化來實現，同樣的可藉助於_mm_madd_epi16指令。

　　我們測試了halcon的gauss_filter 的速度，測試程式碼如下所示：

HalconCpp::HObject hoImage0;
    HalconCpp::ReadImage(&hoImage0, "D:\\1.bmp");

    int max_iter = 100;
    int multi = 3;
    timepoint tb;
    long long tp;

    static  int w[] = { 3, 5, 7, 9, 11, 13, 15, 21, 31, 41, 51 };
    static  int h[] = { 3, 5, 7, 9, 11, 13, 15, 21, 31, 41, 51 };
    HalconCpp::SetSystem("parallelize_operators", "false");
    HalconCpp::HObject hoImageT;
    for (int i = 0; i < 5; i++)
    {
        tb = time_now();
        for (int k = 0; k < max_iter; ++k)
            HalconCpp::GaussFilter(hoImage0, &hoImageT, w[i]);
        tp = time_past(tb);
        std::cout << "GaussFilter " << w[i] << " use time:" << tp / max_iter/1000 << "ms" << std::endl;
    }

　　測試的結果如下：

　　為了測試的公平，我們關閉了halcon的多執行緒優化方面的功能，即使用瞭如下的語句：

HalconCpp::SetSystem("parallelize_operators", "false");

　　我也對我優化後的演演算法進行了速度測試，主要耗時如下表所示：

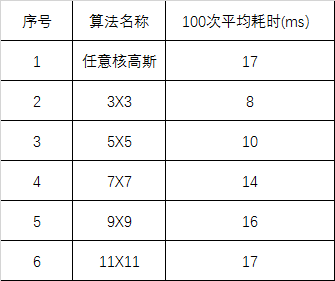
　　和halcon相比，基本在同一個數量級別上。

不過halcon的smooth_image似乎非常的慢，即使我不用其"gauss"引數，同樣的圖片，其耗時如下所示：

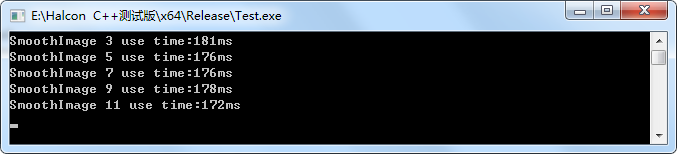
　　呼叫程式碼為：

HalconCpp::SmoothImage(hoImage0, &hoImageT, "deriche1", w[i]);

　　但是說明一點，smoothimage的deriche1引數耗時和sigma值無關。

　　最近關於高斯模糊方面的我寫了不少文章，都綜合在我的SSE優化DEMO裡，最近我也把這個DEMO做了更好的分類管理，如下圖所示：